考虑过盈配合的悬架控制臂焊缝疲劳分析

孔闯

（合创汽车科技有限公司，广州 511455）

1 研究背景

悬架系统作为汽车底盘重要组成部分，起到支撑车体及缓冲路面冲击等作用。通过金属管材焊接、过盈装配形成的控制臂在结构设计中较为常见，如图1 所示，该控制臂具有结构简单、成本低等特点。

图1 汽车悬架控制臂

某车型悬架控制臂在整车耐久试验中发生了耐久失效问题，控制臂端头的套管在焊缝附近发生断裂，衬套从套管中脱出（图2）。

图2 控制臂耐久试验失效

对失效零件进行了材料成分、断口、金相等分析，发现裂纹源位于套管焊接位置（图3~图4），未发现零件存在制造缺陷。该控制臂在设计阶段进行了焊缝疲劳分析，但未考虑过盈配合产生的应力对外套管疲劳寿命的影响，初步判断这是导致控制臂疲劳寿命设计不足的原因。

图3 控制器耐久失效件

图4 失效开裂套管

2 过盈配合应力计算

2.1 过盈配合理论计算

在机械结构中很多零件采用过盈配合的方式进行装配，通过过盈配合产生的压力及摩擦力使零件联结到一起，并可以承载外界输入的载荷而不发生内外筒分离、变形等失效[1]。

本研究中的控制臂内外筒截面如图5 所示，可认为是薄壁圆筒（内管）和厚壁圆筒（外管）的过盈配合。

图5 套管过盈配合截面

国内外针对过盈配合进行过大量研究，各国相继制定了关于过盈配合的设计标准，过盈配合的设计计算主要为理论计算及有限元方法计算[2]。

根据组合圆筒理论，可由公式（1）计算内外筒结合压力[3]。本研究的控制臂根据试验经验设置过盈量平均为0.15 mm。

式中，P为结合压力；Δ 为过盈量；E1、E2分别为外筒、内筒弹性模量；μ1、μ2为外、内筒泊松比；r1为结合半径；r2为外筒半径；r为内筒平均半径；t为内筒厚度。

根据过盈量计算得到配合压力P，从而通过公式计算内外筒过盈配合产生的径向应力σr、切向应力σθ。对于内筒的应力计算，薄壁圆筒分析理论认为切向应力在筒壁厚度范围内为常量，且沿着筒壁厚度方向没有压力梯度。

根据第四强度理论，计算内筒最大von Mises应力为357 MPa，位于内筒的内壁。

对于外筒过盈配合的应力，可根据拉美公式进一步计算得到。

计算外筒最大von Mises 应力为220 MPa，位于外筒的内壁。

2.2 过盈配合有限元方法计算

有限元方法在解决各类工程领域问题中得到广泛应用，经过几十年的发展，对于非线性等复杂的工程问题有限元方法也可以计算。

使用有限元方法对过盈配合应力进行计算[4]，将内外筒简化为四边形壳单元组成，单元尺寸为4 mm，单元数量为616 个，过盈量为0.15 mm，有限元方法计算内外筒应力如图6 所示。

图6 过盈配合有限元计算

通过理论计算及有限元方法计算的过盈配合应力对如表1 所示，两种方法的应力计算结果较为一致，可认为过盈配合有限元结果是可靠的。

表1 过盈配合应力计算对比

计算结果显示内筒的应力已经远大于材料屈服极限275 MPa，内筒已经进入屈服阶段，故计算过盈配合应力需考虑材料非线性。在计算模型中添加材料非线性曲线，当内筒应力达到屈服极限后，根据材料曲线进行非线性计算内筒材料屈服后的应变与应力，对于计算过盈配合的应力更加准确。

考虑内筒的材料非线性曲线重新计算过盈配合应力如图7 所示，内外筒应力276 MPa，略超过屈服极限，外筒应力为160 MPa，较线性计算结果有一定降低。

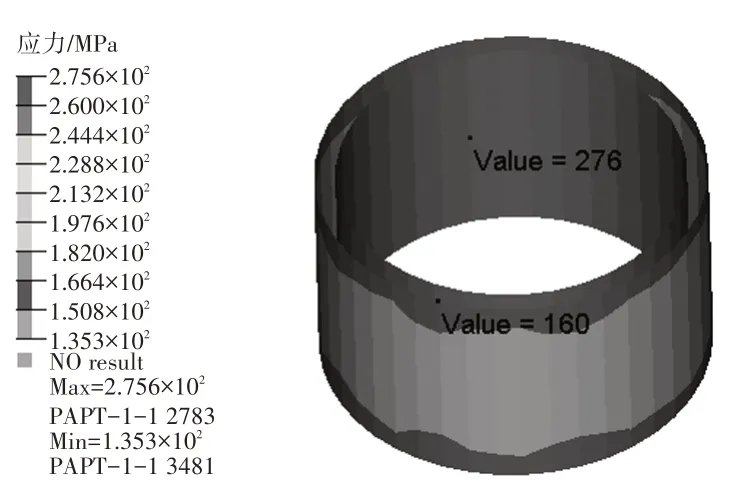
图7 过盈配合非线性有限元计算

对整个控制臂的过盈配合应力进行计算，如图8 所示，由于外筒和中间杆进行了焊接，外筒的刚度发生了变化，存在一定的应力集中，外筒应力增加到167 MPa，而内筒应力无明显变化。

图8 控制臂过盈配合有限元计算

3 焊缝疲劳分析

3.1 耐久载荷等效处理

为了比较全面地验证整车耐久性能，一般完整的整车耐久试验包含多种工况，控制臂在石块路、坑洼路工况的载荷如图9、图10 所示。

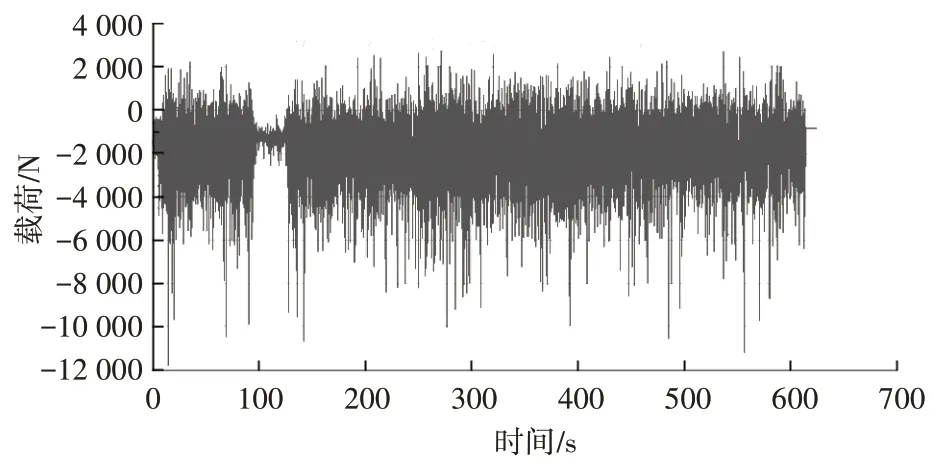
图9 石块路工况控制臂载荷

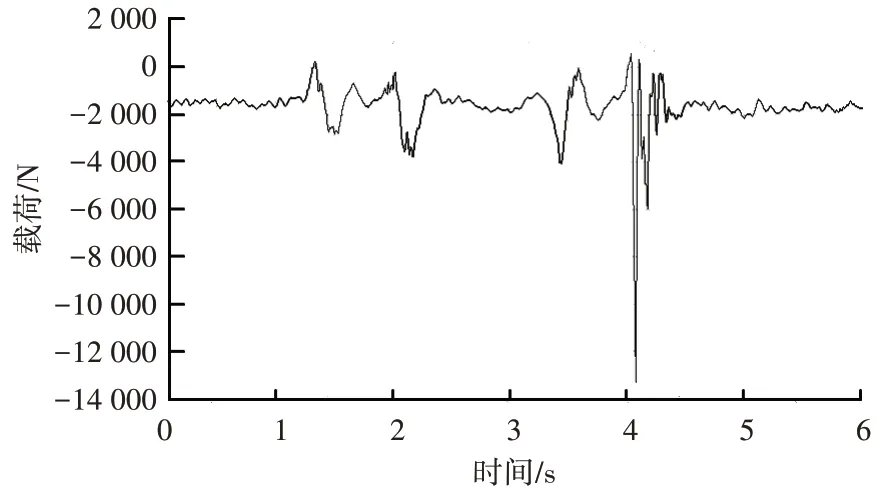
图10 坑洼路工况控制臂载荷

零件的有限元疲劳分析方法，根据载荷类型可分为静载（准静态）疲劳分析方法、瞬态疲劳分析方法、振动疲劳分析方法[5]。本研究使用静态疲劳分析方法，由于考虑过盈配合产生的应力，且施加载荷后控制臂内外筒的变形为非线性，故无法使用各通道单位载荷应力叠加方式获得应力历程，而是用准静态方式直接加载载荷计算零件单一工况的应力历程，然后串联各工况应力历程进行疲劳分析。

根据整车耐久试验的规范，将所有试验工况按照各工况的循环次数组合成完整的载荷时域历程如图11 所示。可以看出完整的耐久试验包含很多工况，而且试验时间也比较长，故考虑把试验工况等效成几个典型工况的循环试验，通过计算等效工况的应力时域历程来计算控制臂的疲劳寿命。

图11 所有耐久试验工况组合

对随机载荷的处理方法一般有功率谱法和循环计数法，功率谱法一般用于频域的振动疲劳分析，循环计数法主要包含峰值计数法、穿级计数法、雨流计数法等。

雨流计数是一种国内外广泛应用的计数方法，一般认为根据雨流计数结果进行疲劳计算更接近实际，大部分的疲劳软件都采用次方法。控制臂载荷的雨流计数如图12 所示，通过幅值和平均值来描述一个载荷循环，通过柱状图的高度以及色标表示这个载荷循环的在整合耐久试验中的循环次数。

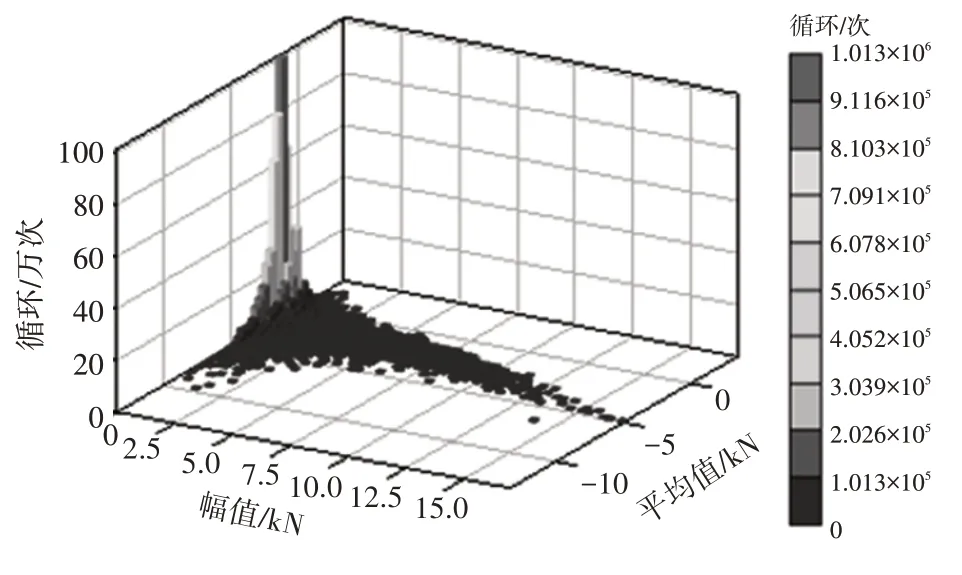
图12 耐久载荷雨流计数

对载荷雨流计数进行分析，按照幅值大小排序及循环次数5%、10%、85%进行工况分级，基于总损伤等效的原则，编制控制臂Block 载荷如表2所示。Block 载荷总循环次数为100 000 次，相比较原始载荷循环次数5 722 616 次有显著降低，而且该Block 载荷便于仿真分析。

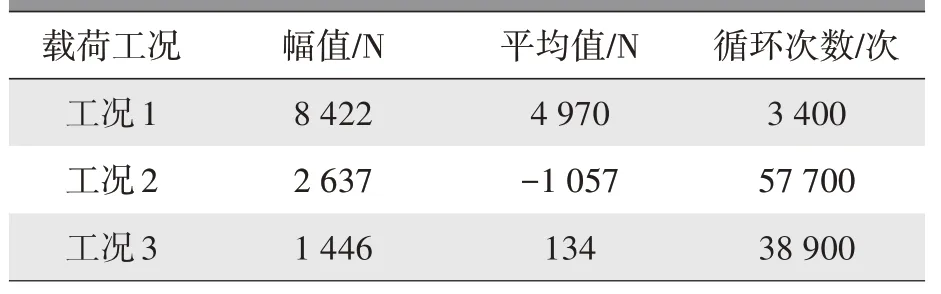
表2 控制臂Block载荷

3.2 焊缝疲劳分析理论

对焊接结构的疲劳分析一般有名义应力评定法、结构应力评定法、局部应力应变评定法和断裂力学评定法[6]。

结构应力评定法通过有限元单元节点力或位移来计算结构应力，结合结构应力及S-N 计算焊缝疲劳寿命，此方法可以降低应力对于单元网格的敏感度。本研究计算焊缝疲劳使用的“VOLVO”方法是基于VOLVO 汽车公司和查尔默斯理工大学最初提出，并与nCode 合作开发。本研究分析使用的是焊缝附近单元的CUBIC 应力，该方法通过单元节点的平动及旋转位移来计算单元应变及应力。

计算焊缝疲劳时需考虑焊缝处的应力状态，如图13 所示，将焊趾处应力分解成弯曲应力和薄膜应力[7]。

图13 焊缝应力组成分解

单元应力弯曲比如公式（2）计算，平均弯曲比如公式（3）计算。

式中，σb为弯曲应力，σm为薄膜应力，σtop为焊趾处应力。

通过单元应力的平均弯曲比来选择S-N 曲线，如图14 所示，当平均弯曲比低于设定的阈值（一般取0.5），选择刚性S-N 曲线；当平均弯曲比等于1 时，选择柔性S-N 曲线；在阈值和1 之间时，使用刚性和柔性S-N 曲线之间的插值曲线。

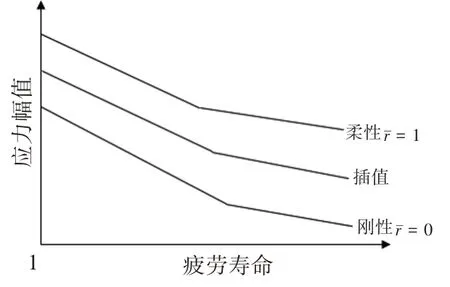
图14 不同弯曲比的S-N曲线

3.3 控制臂焊缝疲劳分析

控制臂焊缝有限元建模如图15 所示，焊缝及焊趾附近单元使用四边形壳单元。

图15 控制臂焊缝建模

控制臂建模后按照编制的Block 载荷表加载三个工况，并将计算的应力结果输入到nCode软件进行焊缝疲劳分析，计算流程如图16 所示。

图16 控制臂焊缝疲劳分析流程

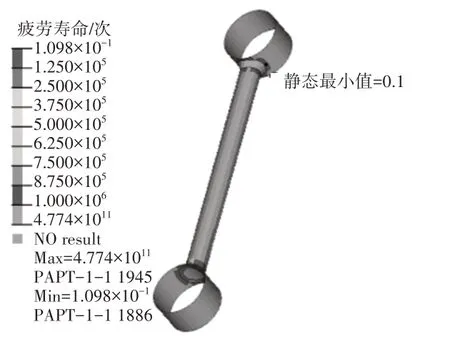
图17 控制臂焊缝疲劳分析结果

控制臂的焊缝疲劳分析结果如17 所示，计算结果显示疲劳寿命为1.1 万次，不满足疲劳寿命大于10 万次的设计要求，说明原设计方案疲劳强度设计不足，与整车试验进度21%时控制臂发生开裂现象相符。

4 控制臂优化设计及验证

4.1 控制臂优化设计

考虑到优化的经济成本、时间周期等因素，选择直接将控制臂端部外筒外径加大、厚壁增加，计算不同厚度方案的焊缝疲劳寿命如图18 所示。原方案外筒壁厚为3.5 mm，当壁厚增加到4.5 mm 时，焊缝疲劳寿命为12 万次，基本达到设计要求；当外筒壁厚增加到5 mm 时，焊缝疲劳寿命为25 万次，有一定安全余量。

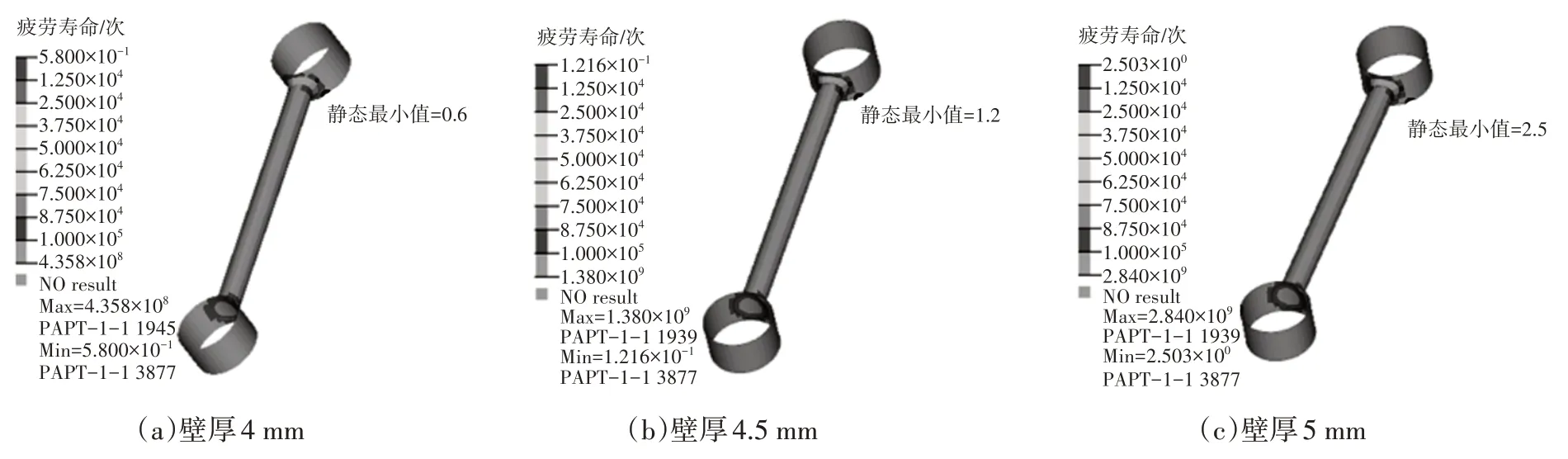
图18 控制臂优化方案分析

4.2 试验验证

为了快速验证优化方案的焊缝疲劳寿命是否达到要求，对不同方案进行了台架耐久验证如图19 所示，试验结果如表3 所示。

表3 各方案仿真与台架试验结果对比 万次

图19 控制臂台架耐久试验

通过台架验证壁厚5 mm 的方案可以满足设计要求，故选择该方案搭载整车耐久试验验证。如图20 所示，优化后的控制臂完成整车耐久试验后未出现开裂问题，说明优化方案有效。

图20 整车耐久试验后状态

5 结论

a.过盈配合的零件进行设计时需考虑过盈装配对零件强度及疲劳寿命的影响，有限元方法可以对过盈配合进行准确的仿真计算；

b.通过合理的耐久载荷等效处理，可以简化疲劳分析及加速试验验证，提高设计及验证效率；

c.本研究使用的焊缝疲劳分析方法对控制臂焊缝疲劳寿命有较好的计算精度，此类零件设计可以参考。