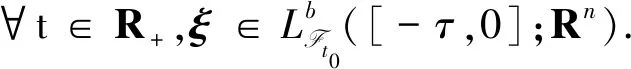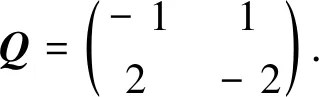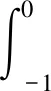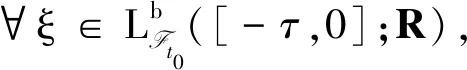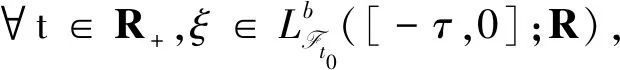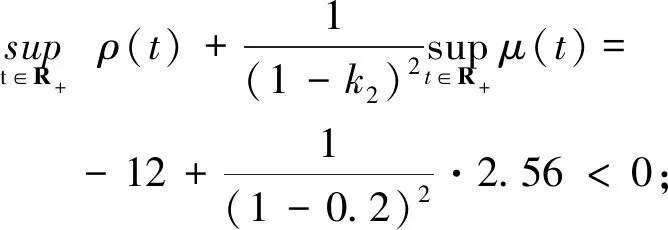一类混合中立型随机泛函微分方程的均方指数稳定性*
赵佳雨
(南京财经大学应用数学学院,江苏 南京 210023)
近年来,随机泛函微分方程成为一个热门的研究话题,这类随机系统未来的状态不仅取决于系统在时刻t的当前状态,还取决于整个时间区间[t-τ,t]上的已有状态[1].随机泛函微分方程在实际问题中有许多应用,但由于系统的演化不仅取决于系统过去的状态,还与系统在许多生活现象中的变化速率有关,因此有学者进一步研究了中立型的随机泛函微分方程[2].此外,由于不稳定的系统环境,随机系统经常会出现随机突变,进而导致这些系统在多个不稳定的状态之间切换.连续时间Markov链是描述这些随机突变的有力工具,如在生态学和随机控制领域,混合随机泛函微分方程就被视为模拟这些系统的有效模型.
研究随机泛函微分方程稳定性问题是一项非常有意义的工作.目前,国内外学者对混合中立型随机泛函微分方程稳定性的研究较多[3-6],且大部分采用的经典而强大的技术都是Lyapunov函数方法[7]、Razumikhin型定理[8]和不动点方法[9].为了进一步丰富和明确一般中立型随机泛函微分方程均方指数稳定性的判据,Plam[10]采用比较原理和反证法来判定,并举例说明了结论的适用性.笔者拟在文献[10]的基础上作改进,即在系统突变的条件下建立新的混合中立型随机模型,并讨论混合中立型随机泛函微分方程均方指数的稳定性.
1 模型描述和预备工作
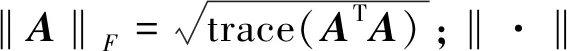
令(Ω,F,{Ft}t∈R+,P)是满足通常条件的完备概率空间,{Ft:t∈R+}是(Ω,F,P)上给定的σ代数流,且流Ft是右连续、单调增的,F0是所有的P零集.{W(t)}t∈R+是一个定义于概率空间上的m维标准布朗运动.假设{r(t),t∈R+}是齐次右连续Markov链,其在有限状态空间S={1,2,…,N}上取值.转移速率矩阵Γ=(γij),由状态i到状态j的转移概率
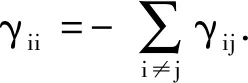
考虑下列混合中立型随机泛函微分方程:
d(x(t)-G(xt))=f(t,xt,r(t))dt+g(t,xt,r(t))dW(t)t∈R+.
(1)
其中:xt={x(t+s),s∈[-τ,0]},是一个C([-τ,0];Rn)值随机过程;
f:R+×C([-τ,0];Rn)×S→Rn;
g:R+×C([-τ,0];Rn)×S→Rn×m;
G:C([-τ,0];Rn)→Rn.
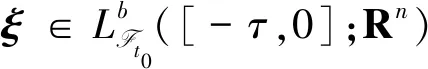
xt0=ξ.
(2)
令C(Rn×[-τ,+∞);R+)为从Rn×[-τ,+∞)到R+的所有连续函数族,C2,1(Rn×[-τ,+∞)×S;R+)为在Rn×[-τ,+∞)×S上的所有连续非负函数V(x,t,i)族,且V(x,t,i)对x连续二阶可微,对t连续一阶可微.对于V∈C2,1(Rn×[-τ,+∞)×S;R+),定义运算符LV:C([-τ,0];Rn)×R+×S→R,
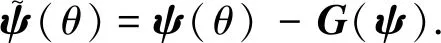
以下记T为某个实数,对于任何区间J=[t0,T]⊂R+,约定Jτ=[t0-τ,T].
定义1称x(t)为方程(1)在t∈Jτ上具初值ξ的解,如果Rn值随机过程x(t)(t∈Jτ)满足以下条件:
(1)x(t)为连续且Ft-适应的C([-τ,0];Rn)值随机过程;
(2){f(t,xt,r(t))}t≥0∈L1(R+;Rn),{g(t,xt,r(t))}t≥0∈L2(R+;Rn×m);
(3)对于∀t∈R+,初值条件(2)满足
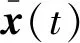
以下结果保证了方程(1)解的存在唯一性:
定理1设I是以t0为左端点的(有限或无限)区间,函数f,g与G满足以下条件:
(ⅰ)局部Lipschitz条件.任给紧区间H⊂I与n∈N+,对于每一个n≥1,存在正常数lJn,使得当t≥0,i∈S,φ,ψ∈C([-τ,0];Rn),‖φ‖∨‖ψ‖≤n时,有
|f(t,φ,i)-f(t,ψ,i)|2∨|g(t,φ,i)-g(t,ψ,i)|2≤lJn‖φ-ψ‖2.
(ⅱ)线性增长条件.任给紧区间H⊂I,存在正常数lJ,使得当t≥0,i∈S,φ∈C([-τ,0];Rn)时,有
|f(t,φ,i)|2∨|g(t,φ,i)|2≤lJ(1+‖φ‖2).
(ⅲ)压缩性条件.存在k1∈(0,1),使得当φ,ψ∈C([-τ,+∞);Rn)时,有
|G(φ)-G(ψ)|≤k1‖φ-ψ‖.
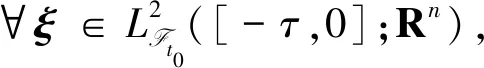
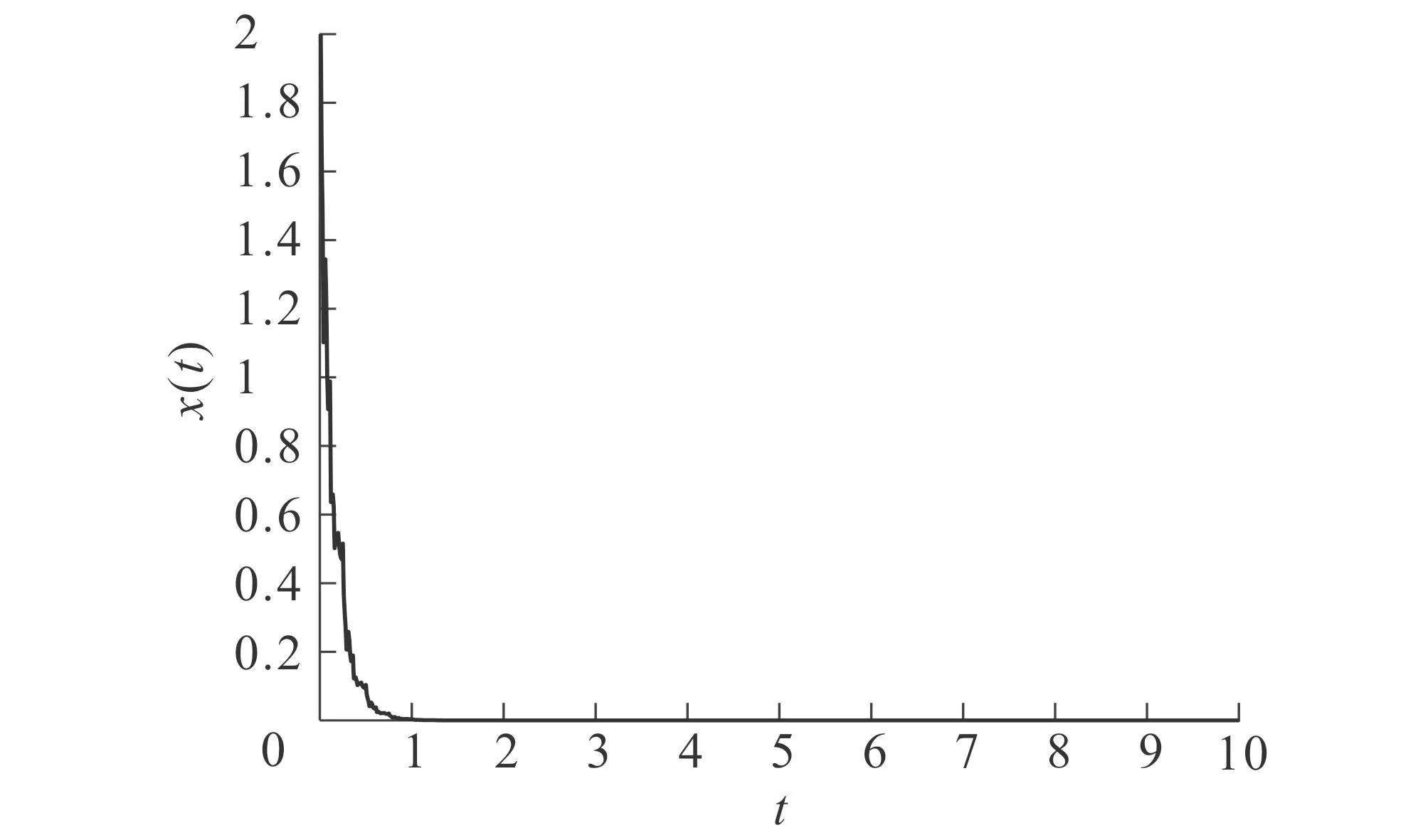
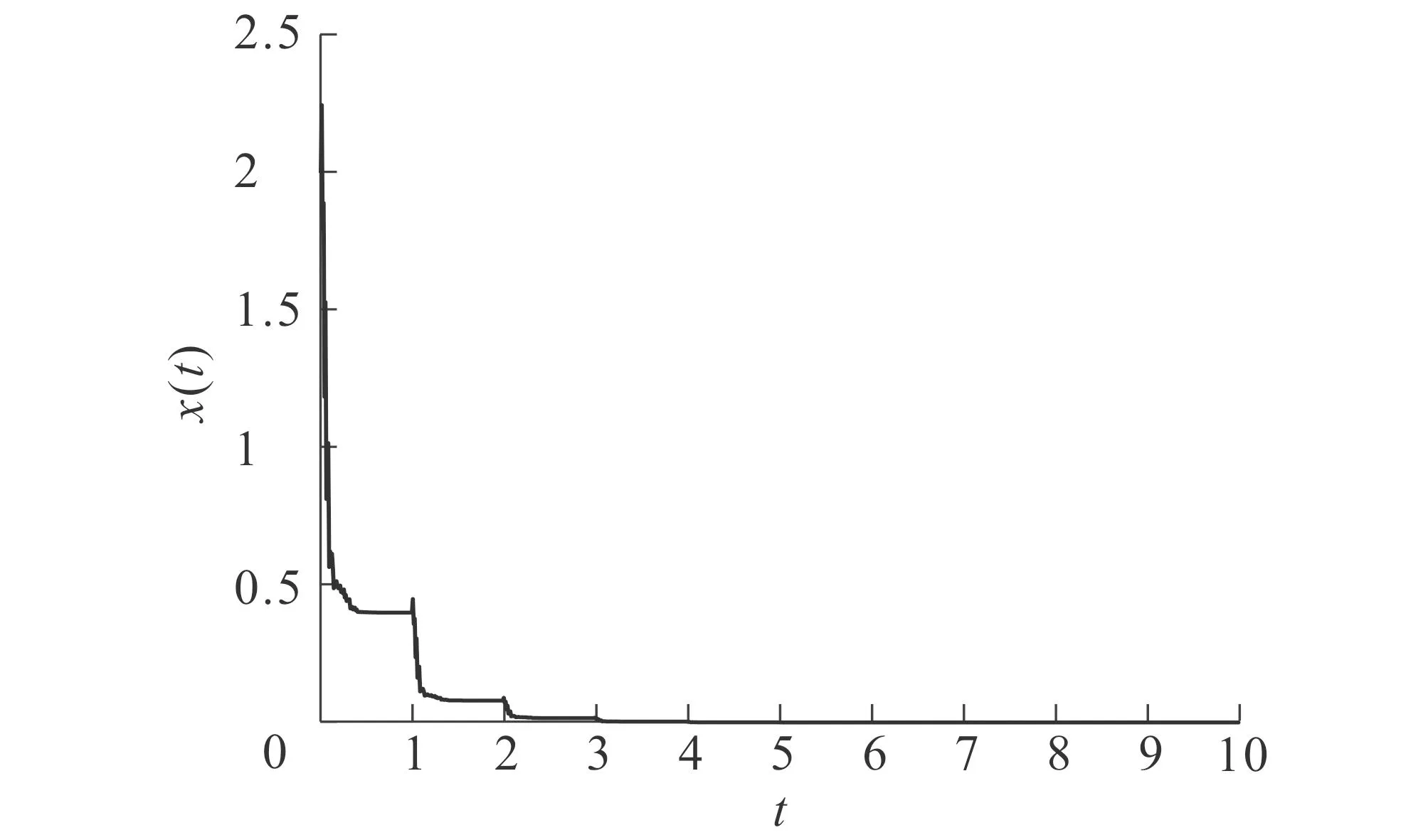
证明(ⅰ)取一停时序列{τk}k≥0,满足0=τ0<τ1<…<τk→+∞,且r(t)在每一个区间[τk,τk+1)上几乎处处为常数.对于∀k≥0,有r(t)=r(τk),τk 对于∀T>0,在方程(1)中,先考虑当t∈[0,T∧τ1]时,有r(t)=r(0),从而方程(1)变为具初值x0=ξ的方程 d(x(t)-G(xt))=f(t,xt,r(0))dt+g(t,xt,r(0))dW(t). (3) 由于r(0)是常数,因此方程(3)是一个中立型随机泛函微分方程.由文献[11]中的定理3.3.2可知,方程(3)在区间[-τ,T∧τ1]上存在唯一连续解. 再考虑当t∈[T∧τ1,T∧τ2]时,有r(t)=r(τ1),从而方程(1)变为具初值xT∧τ1的方程 d(x(t)-G(xt))=f(t,xt,r(τ1))dt+g(t,xt,r(τ1))dW(t). (4) 由于r(τ1)是常数,因此方程(4)是一个中立型随机泛函微分方程.由文献[11]中的定理3.3.2可知,方程(4)在区间[T∧τ1,T∧τ2]上存在唯一连续解. 重复以上过程发现,方程(1)在区间t∈[-τ,T]上存在唯一解x(t).由于∀T>0,因此方程(1)在t≥-τ上存在唯一解x(t). 于是 由Gronwall不等式,可得 因此 为了探究方程(1)的均方指数稳定性,记方程(1)的解为x(t,t0,ξ),如果ψ=0,假设G(ψ)=0,且f(0,t,i)=0,g(0,t,i)=O,∀t∈R+,i∈S,那么方程(1),(2)在t0处有平凡解x(t)=0. (5) (6) 再假设存在局部有界Borel可测函数ρ(·):R+→R和ζ(·,·):R+×R-→R+,使得对于∀t∈R,ψ∈C([-τ,0],Rn),i∈S,有 (7) (8) 则方程(1)的零解是均方指数稳定的. 证明令x(t)=x(t;t0,ξ),是方程(1),(2)的解,t∈Jτ. (9) 则 (10) 假设(9)式成立,则对于∀ε∈(0,1),有 于是由(6)式,可得 从而由(9)式,可得 于是 (ⅱ)证明方程(1)的零解是均方指数稳定的. 固定M>2+2k2.考虑连续函数 X(t)=E|x(t)-G(xt)|2t≥t0, 由X(t)的定义、Cp不等式及(6)式,可得 X(t0)=E|x(t0)-G(xt0)|2≤E(|x(t0)|+|G(xt0)|)2≤2E|x(t0)|2+ 即X(t0) 下证 X(t)≤Y(t)t≥t0. (11) (反证法)假设存在t1>t0,使得X(t1)>Y(t1).由连续性可得 X(t)≤Y(t)t∈[t0,t*], (12) X(tn)=Y(tn), X(t*)=Y(t*). (13) 令g1(ψ,t,i),g2(ψ,t,i),…,gm(ψ,t,i)为g(ψ,t,i)的列向量,明显有 又由(7)式,可得 从而由Fubini定理,可得 从而当t=t*时,由(8)式,可得 M1eαt*e-β(t*-t0) 所以, 这与(13)式矛盾,故原假设不成立,从而(11)式成立.于是, 由(ⅰ),可得 故由(5)式可知方程(1)的零解是均方指数稳定的.证毕. (14) (15) 证明(6),(7)式通过不等式两边求期望可分别得到(14),(15)式,因此将定理2中的(6),(7)式分别换为(14),(15)式,证明类似.证毕. (16) (17) 所以由(17)式可推得(8)式.将定理3中的(8),(15)式分别换为(17),(16)式,证明类似.证毕. 由定理2~4可得以下结果: 推论1假设(8),(9)式或(16),(17)式成立.若 (18) 则方程(1)的零解是均方指数稳定的. 注1由(18)式可知,对于∀t∈R+,有 从而(8)式成立.推论1来源于定理2和定理3. 推论2假设(14),(16)式成立.若 (19) 则方程(1)的零解是均方指数稳定的. 注2由(19)式,可得 从而(17)式成立.推论2来源于定理4. 例1考虑下列具有Markov切换的中立型随机延迟微分方程: d(x(t)-u(x(t-τ)))=f(x(t),x(t-τ),t,r(t))dt+ g(x(t),x(t-τ),t,r(t))dW(t)t≥t0>0. (20) 其中:τ>0;u:Rn→Rn,f:Rn×Rn×R+→Rn,g:Rn×Rn×R+→Rn×m,是连续函数,满足对于∀t≥0,有u(0)=0,f(0,0,t,i)=0,g(0,0,t,i)=O;W(t)是一维标准布朗运动.f和g满足局部Lipschitz条件,u是一个压缩映射,即 |u(x)-u(y)|≤c|x-y|x,y∈Rn,c∈(0,1). (21) 假设存在正常数αi>0,i=1,2,使得对于t∈R+,x,y∈Rn,i∈S,有 (22) 则方程(20)的零解是均方指数稳定的. 证明(ⅰ)由(21)式,可得 故(14)式成立. (ⅱ)由(22)式,可得 -α1E|ξ(0)|2+α2E|ξ(-τ)|2. 对于∀ε∈(0,1),有 E|ξ(0)|2≥E(|ξ(0)-G(ξ)|2)+E(|G(ξ)|2)-2E(|ξ(0)-G(ξ)||G(ξ)|)≥ 即 从而 故(16)式成立. 特别地,易证中立型随机延迟微分方程 d(x(t)-0.2x(t-0.25))=f(x(t),x(t-τ),t,r(t))dt+ g(x(t),x(t-τ),t,r(t))dW(t) (23) f(x(t),x(t-τ),t,1)=-8x(t)+1.6x(t-0.25)-5(x(t)-0.2x(t-0.25))3, f(x(t),x(t-τ),t,2)=-2.5(x(t)-0.2x(t-0.25))3, 图1 方程(23)的样本路径Fig. 1 Sample Path of the System (23) 图1示出了方程(23)的样本路径,由图可见零解是稳定的. 例2考虑下列具有Markov切换的中立型随机泛函微分方程: d(x(t)-0.2x(t-1))=f(xt,t,r(t))dt+ g(xt,t,r(t))dW(t), (24) f(xt,t,1)=-6x(t)+1.2x(t-1),f(xt,t,2)=-5x(t)+x(t-1), 其中ρ(t)=-12,μ(t)=2.56,于是(16)式成立;当i=2时, 其中ρ(t)=-10,μ(t)=0.64,于是(16)式也成立. (ⅲ)由(ⅱ)可知:当i=1时, 图2 方程(24)的样本路径Fig. 2 Sample Path of the System (24) 当i=2时, 于是(19)式成立. 综上,由推论2可知,方程(24)的零解是均方指数稳定的.证毕. 图2示出了方程(24)的样本路径,由图可见零解是稳定的.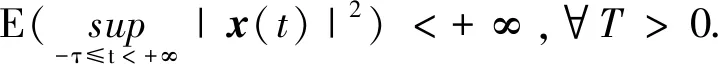
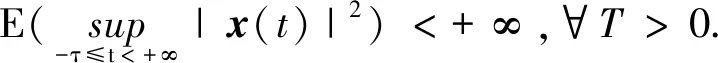
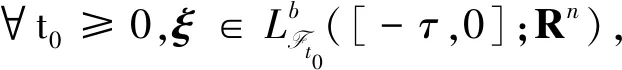
2 均方指数稳定性
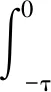
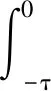
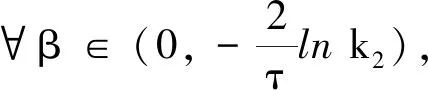
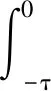
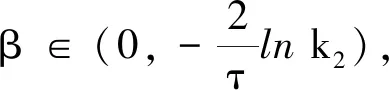
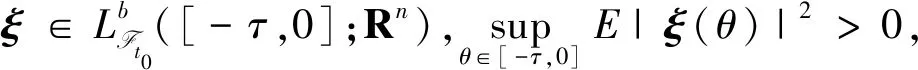
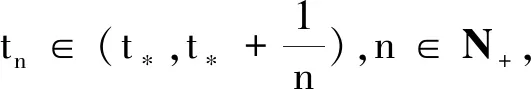
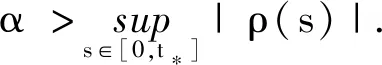
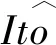
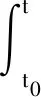
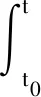
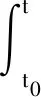
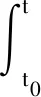
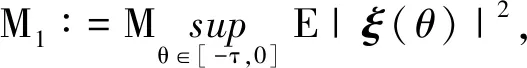
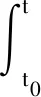
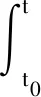
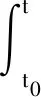
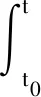
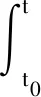
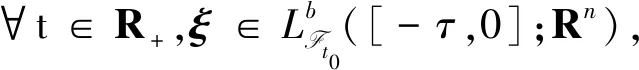
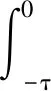
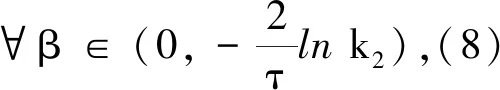
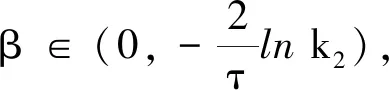
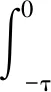
3 数值算例