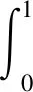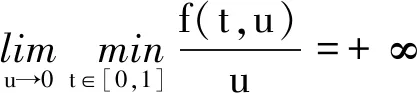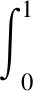Caputo-Fabrizio型分数阶微分方程两点边值问题正解的存在性*
王兰芳
(吉首大学数学与统计学院,湖南 吉首 416000)
1 问题的提出
分数阶导数及分数阶微分方程被广泛应用于诸多领域.这类分数阶导数(如Riemann-Liouville型和Caputo型分数阶导数)及其对应的分数阶积分被赋予奇异核,有利于刻画具有记忆效应的演化过程[1],但核的奇异性给问题的数学处理带来困难.许多动力学过程的延迟记忆效应可用含非奇异核的积分进行研究,如Stanislavsky等[2]和Harko等[3]利用含非奇异指数核的积分对这类过程进行了建模.因此,根据不同的应用场景和约束条件,经典的分数阶导数和积分应作进一步推广.目前,新引进的含非奇异核的分数阶导数和积分主要分为2类:非奇异指数核,以Caputo-Fabrizio型分数阶导数为代表[4];非奇异Mittag-Leffer核,以Atangana-Baleanu型分数阶导数为代表[5].含非奇异核的分数阶导数及分数阶微分方程已成为一个热门的研究领域[6-9].
在Caputo等[4]和Atangana等[5]给出的含非奇异核分数阶导数的定义中,导数的阶介于0~1之间,这一点会影响这类导数的应用范围.为此,Abdeljawad[10-11]将文献[4-5]中的定义推广到高阶情形.其中,Abdeljawad[10]定义了高阶Caputo-Fabrizio型分数阶导数与积分,系统地研究了它们的主要性质.他们还研究了几类初值与边值问题解的存在性,特别地,建立了一类阶介于2~3之间的线性分数阶方程边值问题解的Lyapunov型不等式.值得注意的是,虽然Abdeljawad[10]给出了原边值问题等价的积分方程,但是积分核并非原问题真正意义上的格林函数,因此没能给出这类边值问题解的存在性结果.笔者拟在文献[10]的基础上,探讨以下这一类含高阶Caputo-Fabrizio型分数阶导数的分数阶微分方程两点边值问题正解的存在性:
(1)
其中f:[0,1]×[0,+∞)[0,+∞),2<α≤3.
2 预备知识
定义1[1]设y∈L1[a,+∞),α>0,定义y的α阶Riemann-Liouville型分数阶积分为(aIαy)(t),
(2)
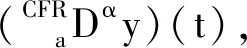
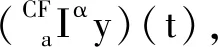
(3)
其中B(α)为规范化函数,B(0)=B(1)=1.
定义2可以通过归纳推广到高阶情形.

(4)
其中β=α-n.
命题1[10]定义3中的导数与积分有以下关系:

(5)

(6)
引理1设h∈L1(0,1),α∈(2,3],则问题
(7)
存在唯一解
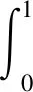
其中格林函数
(8)
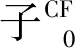
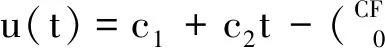
(9)
再由(2),(3),(4)式,对(9)式进行等价变形处理,得
(10)
由边界条件,可确定常数
将c1及c2代入(10)式中,进一步变形可得
其中
G1(t,s)=2(1-β)(1-s)+βt(1-s)2-2(1-β)(t-s)-β(t-s)20≤s≤t≤1,
G2(t,s)=2(1-β)t(1-s)+βt(1-s)20≤t≤s≤1,
为了给出格林函数G(t,s)的基本性质,先引入相关参数和函数.记
引理2θ(t)Φ(s)≤G(t,s)≤Φ(s).
证明一方面,由(8)式可知,对于∀s,t∈[0,1],有
2B(β)G(t,s)≤2(1-β)t(1-s)+βt(1-s)2≤2(1-β)(1-s)+
β(1-s)=(2-β)(1-s)≤2(1-s),
于是导出G(t,s)≤Φ(s).
另一方面,当0≤t≤s≤1时,
2B(β)G(t,s)=2(1-β)t(1-s)+βt(1-s)2≥2σt(1-t)(1-s)≥σt(1-t)(1-s),
即θ(t)Φ(s)≤G(t,s);当0≤s≤t≤1时,
2B(β)G(t,s)=2(1-β)t(1-s)+βt(1-s)2-2(1-β)(t-s)-β(t-s)2=
(1-t)(2(1-β)s+β(t-s2))≥σ(1-t)(t+2s-s2)≥
σt(1-t)(1-s)),
即θ(t)Φ(s)≤G(t,s).证毕.
3 主要结果及其证明
基本假设:
(H)f为[0,1]×[0,+∞)上非负连续二元函数,且关于2个变元具有连续偏导数.

P={u∈B:u(t)≥θ(t)‖u‖,t∈[0,1]}.
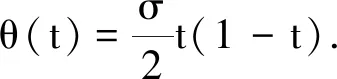
给定正数r,定义B中的开球Ωr,Ωr={u∈B:‖u‖ (11) 条件(H)确保算子A有意义且具有以下几个性质: 引理4若条件(H)满足,则A(P)⊂P. 证明对于∀u∈P,由(11)式及引理2,可得 及 这导出(Au)(t)≥θ(t)‖Au‖,因此A(u)∈P.再由u的任意性,可得A(P)⊂P.证毕. 在条件(H)下,用标准化的过程和方法不难证明引理5,在此省略. 由引理1及引理2,可得以下结果: 引理6若条件(H)满足,则函数u(t)为边值问题(1)的正解,当且仅当它是算子A在锥P中的不动点. 定理1若条件(H)满足,且 则边值问题(1)至少存在1个正解. f(t,u(t))≥ρu(t)t∈[0,1],u∈P∩∂Ωr1. (12) 由(11),(12)式及引理2,可得以下估计:对于∀t∈[τ,1/2],u∈P∩∂Ωr1,有 因此,对于∀u∈P∩∂Ωr1,有‖A‖≥‖u‖. 记ρ2=max{f(t,u):t∈[0,1],u∈[0,ρ1]},则由已得到的估计,进一步可得 f(t,u)≤εu+ρ2t∈[0,1],u≥0. (13) 因此,对于∀u∈P∩∂Ωr2,有‖A‖≤‖u‖. 类似地,可证明以下结果: 定理2若条件(H)满足,且 则边值问题(1)至少存在1个正解.