基于深度学习的期末复习课堂教学模式探究
张丽珊


摘要:新数学课标指出,数学教育要以有利于学生全面发展为中心,以提供有价值的数学和倡导有意义的学习方式为基本点.教师在平时的教学过程中,要着重培养学生的学习积极性,进而使其能够进行独立思考并解决数学问题,找到通往深度学习的途径.而复习课对学生而言,重要性不言而喻.如何上好期末复习课,选择怎样的课堂教学模式才能实现高效减负呢?以人教版第二十二章“二次函数”复习第一课时为例 ,按“课前诊断”“课堂探究”“课堂反馈”“课后作业”“中考链接”这几个环节来探究期末复习课堂教学模式.
关键词:数学活动;深度学习;核心素养
1 文本分析
二次函数属于函数与方程,是初中代数领域的重要内容,本节课重点复习二次函数的定义、图象与性质等基础知识,引导学生将知识点梳理成知识结构图,难点在于拓展迁移应用函数的图象与性质解决问题.
2 学情分析
学生已复习了“方程”“一次函数”“反比例函数”,在此基础上系统梳理二次函数解析式的三种表达方式,建构知识体系,发现知识的“新内涵”,进而获得研究函数的通用方法,类比归纳总结,帮助学生领悟数学知识,提升深度学习能力[1].
3 目标解析
(1) 知识技能:二次函数的定义、图象与性质.
(2)数学思想:数形结合思想、特殊到一般、分类思想、类比归纳思想.
(3)数学素养:模型意识,研究函数的方法;结合图象,发挥好几何直观的作用[2].
4 教学实施
活动一:课前诊断 (利用基础题,了解学生对双基的掌握情况).
(Ⅰ)二次函数的定义
概念:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数.其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
需要注意的是:函数解析式是整式;整理后自变量的最高次数是2;二次项系数不等于0.
(1)二次函数y=-x2+2x的二次项系数是[CD#3],一次项系数是[CD#3],常数项是[CD#3].
(2)已知函数y=(k2-9)x2+(k+3)x+17,
当k为何值时,该函数为一次函数?当k为何值时,该函数为二次函数?
易错点:忽略二次项系数不等于0.
(Ⅱ)二次函数的图象与性质
(3)抛物线y=x2-4的顶点坐标是[CD#3].
(4)函數y=(x-1)2+2的最小值是[CD#3].
(5)二次函数y=-x2-2x的开口[CD#3],对称轴是[CD#3].
师生活动:教师精心选择内容,回顾本章知识;学生5分钟限时完成上述诊断题.
意图说明:通过课前诊断快速了解学生对基础知识、基本技能的掌握情况,精准诊断便于有向有序地进行复习.
活动二:课堂探究(借助典型例题及问题串,引导学生梳理知识).
例1 已知二次函数y=ax2+bx+3中的x,y满足表1:
(1)求该二次函数的解析式(顶点式与一般式).
(2)①开口方向:[CD#4].
②对称轴:[CD#5].
③顶点坐标:[CD#5].
④图象与x轴的交点A,B的坐标:[CD#5].
⑤图象与y轴的交点C的坐标:[CD#5].
⑥图象与y轴的交点关于对称轴的对称点的坐标:[CD#5].
⑦画出函数的图象.
⑧当x=[CD#3]时,函数的最值为[CD#3].
⑨当[CD#3]时,y=0;当[CD#3]时,y>0;当[CD#3]时,y<0.
B10图象在x轴上截得的线段的长为[CD#3].
B11三角形ABC的面积为[CD#3].
B12当x[CD#3]时,y随x的增大而增大;当x[CD#3]时,y随x的增大而减小.
B13要得到抛物线y=x2,则如何平移二次函数y=ax2+bx+3的图象?
师生活动:给予学生适当时间自主探究,再与小组同伴进行交流.还可以提出其他问题,如“若点P在抛物线上,且点P到x轴的距离为2,求点P的坐标”.最后归纳总结:
(1)函数的三种表示形式:列表、图象、解析式.
(2)二次函数知识结构图如图1.
(3)数学思想:数形结合思想、分类思想、特殊到一般等.
(4)研究函数的基本思路.
意图说明:通过对近年来涉及本章知识点的质检题或中考题的整理,以典型例题引领,利用问题串重新建立知识关联,从不同角度看待原有知识,促进学生对二次函数的深度理解,进而形成高阶思维能力.引导学生自主回顾知识,归纳总结并绘制知识结构图,帮助学生构建并内化知识间的内在联系,从逻辑推理角度将知识系统化,并形成可迁移能应用的知识网络图,真正做到融会贯通,“温故而知新”,进而找到通向深度学习的有效途径.重视渗透思想方法及积累复习课活动经验[3].
活动三:练一练(前后联系,加深对知识的理解).
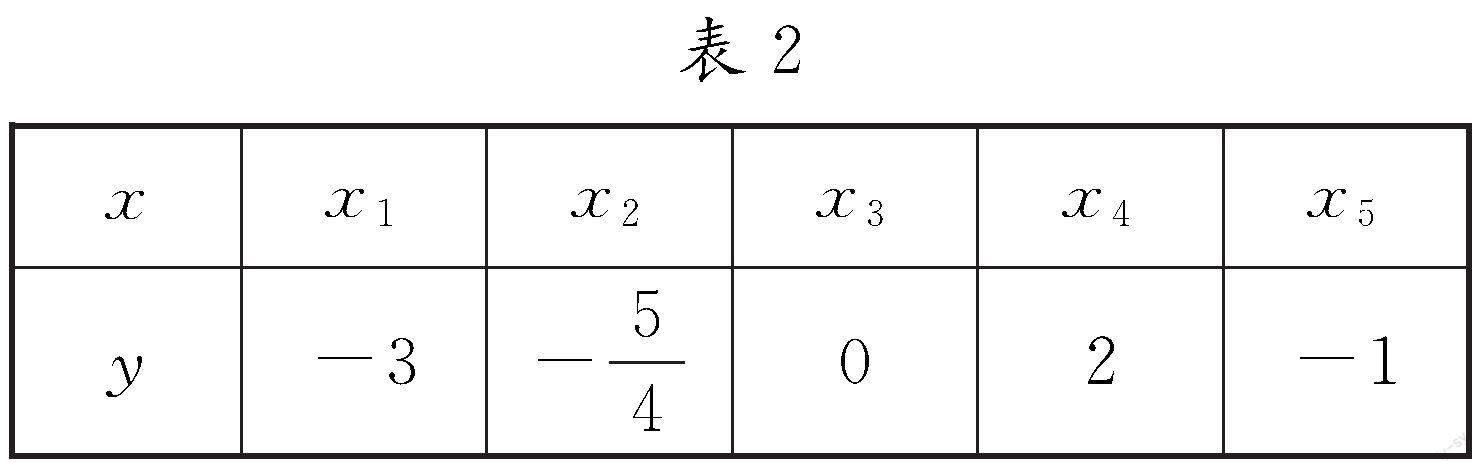
(1)(2017-2018学年厦门)某二次函数的几组对应值如表2所示.若x1<x2<x3<x4<x5,则该函数图象的开口方向是[CD#3].
生1:例1与练习(1)相似,都是以表格形式呈现.
生2:可以令x1,x2,x3,x4,x5分别为1,2,3,4,5,画出示意图即可求解,即特殊值法和图象法.
生3:我发现“当x1<x2<x3<x4时,y随x的增大而增大,当x4<x5时,y随x的增大而减小”,可知函数图象开口向下,即函数性质法.
师:几位同学都说得很好,还有补充的吗?
生4:不管是特殊值结合图象法还是函数性质法都是解决函数问题的常用方法.
生5:若是含参问题,可先尝试用特殊值法来理解题意,结合图象直观感悟,再用函数性质法解题验证.
师:同学们能够反思总结解题方法,运用函数的本质思考并形成解题策略,具有未来数学家的潜质.
意图说明:展示学生求解的思路,并邀請学有余力的学生尝试析题,总结归纳方法,积累解题经验.此题虽是含参问题,利用特殊值法,数形结合将其转化为与例1相似的问题,既巩固基础知识又考查学生转化思想及知识迁移能力,让学生在不断思考的过程中感悟转化、一般到特殊、数形结合等数学思想.通过分享不同的解题方法,开拓思维,培养学生多角度、全方位思考的深度学习能力,提升核心素养.
活动四:拓展提升(不断拓展,形成解题策略).
例2 (2015年厦门中考第24题改编)已知实数a,b满足a-b=1,a2-ab+2>0,当1≤x≤2时, 函数y=ax2(a≠0)的最大值与最小值之差是1,求a的值.
生1:好多参数啊!从何入手呢?
生2:先求a的值.可用含a的代数式表示b,即b=a-1.
生3:将 b=a-1代入a2-ab+2>0,得a>-2.这样还是无法判断a的符号,也就无法确定函数的增减性.
生4:虽然无法判断a的符号,但可以分-2<a<0与a>0两种情况进行讨论.
师:同学们从一开始的“不知所措”到“步步解套”,最后迎刃而解,能否再对其进行反思总结?
生6:此函数问题主要考查函数性质,利用函数与方程思想,结合数学分类讨论等解决问题.
生7:认真审题,推理能力、运算能力是考查重点.
师:分析得太棒了,可以取代老师了!那能否帮老师改编题目呢?
变式 已知实数a,b满足a-b=1,a2-ab+2>0,当-1≤x≤2时, 函数y=ax2(a≠0)的最大值与最小值之差是1,求a的值.
教师追问:还可以再改编吗?例如将“函数y=ax2(a≠0)” 变为“函数y=a(x-1)2(a≠0)”,找出解题策略.
意图说明:将例2的条件“当1≤x≤2时”改编为“当-1≤x≤2时”,其他条件不变,此时由于自变量取值范围的改变导致最大与最小值的变化进而引起a值的改变.加深对二次函数图象与性质的理解,深化对知识的迁移,进而提升深度学习能力,积累经验,增进对数学思想方法的理解,提高核心素养.
活动五:课堂反馈 (有效反馈,精准辅导).
(1)将抛物线y=-3x2向上平移一个单位,再向右平移2个单位后,得到的抛物线解析式是[CD#3].
(3)(B层)已知二次函数的顶点坐标为(3,-1),且过点(2,0) ,求这个二次函数的解析式.
(A层)已知二次函数y=x2+bx+c的图象过点(2,0)且对称轴过点(3,1),求这个二次函数的解析式.
意图说明:课堂反馈是教学中的一个重要环节.保证每节课有适当的训练时间,及时运用刚学到的知识解决问题,灵活地“做”,不死记硬背.让学生独立限时完成,教师巡视.在双减政策下,减轻学生过重的课外负担,如第(3)题可以选择做A层或B层,并且可用来检验教学效果,精准反馈学情,有利于教师课后有针对性地进行辅导,布置拓展性的作业,使学生拥有高阶思维能力,进一步走向深度学习.
活动六:课后作业(巩固教学内容,中考链接,培养学生解决问题的能力).
(1)对于一元二次方程x2-2x+1=0,根的判别式b2-4ac中的b表示的数是().
A.-2
B.2
C.-1
D.1
(2)已知某二次函数,当x<1时,y随x的增大而减小;当x>1时,y随x的增大而增大,则该二次函数的解析式可以是().
A.y=2(x+1)2
B.y=2(x-1)2
C.y=-2(x+1)2
D.y=-2(x-1)2
(3)(2023年福建中考第24题)二次函数y=ax2+bx+3的图象过A(1,0),B(3,0)两点,顶点为
意图说明:结合近几年质检题或中考题,让学生感受中考气氛.第(1)题与第(2)题考查方程与函数知识,都属于“四基”内容,以增强学生学习数学的自信心,激发学生学习热情.第(4)题属于二次函数的实际应用问题,引导学生关注实际生活问题,强化数学模型意识,感悟知识的迁移,获取通向深度学习的途径.
5 反思与感悟
在双减背景下,数学复习课堂采用何种教学模式提升学生数学能力与素养给新时代数学教师带来了挑战.由于是复习课,因此可以引导学生在课前阅读教材并绘制知识结构导图,或以手抄报的形式关联各知识点,以个体的视角呈现重难点及典型例题,并在课堂中与同学分享交流讨论,再通过拓展题的解析与变式,发展学生思维素养,促进教学相长,构建高效有趣的复习课堂.
以活动引导学生思考、观察、猜想、验证,合理运用教材资源,让复习课不再枯燥,这样的深度学习才能拓宽学生视野,有利于学生提高认知,积累有意义的活动学习经验.
总之,基于深度学习的期末复习教学应
关注教学内容的本质,从知识技能、数学思考、问题解决、情感态度等方面使学生达成课程目标,获得适应社会生活和发展所需的数学知识,提升数学核心素养.
参考文献:
[1]王妍,龚吕乐.利用函数求最值[J].中学数学教学参考,2021(5):65-68.
[2]中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
[3]吴春.圆的基本性质[J].中学数学教学参考,2021(5):36-38.

