关于的个数问题
张 悦, 戴浩波
(安徽理工大学 数学与大数据学院, 安徽 淮南 232001)
记P表示所有素数的集合, 字母p1,p2,p3是P中的元素.Z表示所有整数的集合.N表示所有正整数的集合, 对于任意n=N定义以下函数:
对于i,j∈{0,1,2}, 考虑均值
本文主要讨论了S1,2(x)的情况.
下面列举一些本文涉及的经典结论.
1993年,Huxley[1]证明了

Rieger[2]证明了
后来, Daniel[3]结合等差数列中素数分布的Barban-Davenport-Halberstam定理[4]改进Rieger[2]关于S1,1(x)的结论, 进一步得出渐进公式
(1)
此外, 直接应用素数定理(文献[5], 定理8.1), 可以得出
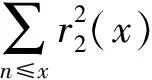
(2)
之后, Plaksin[7]推出
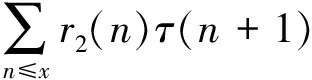
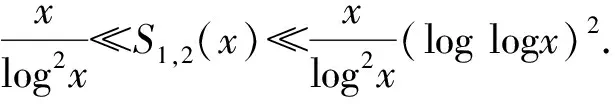
定理1 当x→∞时, 有
S1,2(x)
1 基本引理
根据Brun筛法[15], 记
(3)
由定义知
1≤g(db)≤g(d)g(b),db≠0.
(4)
引理2.1 令x>0,s>0,k>0则有
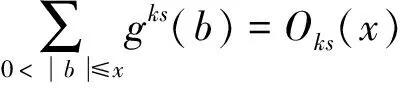
引理2.2 令x>0,s>0,k>0 则有
证明 见Rieger (文献[2], 引理2).
引理2.3 令x>0,s>0则有
证明见Rieger (文献[2], 引理2).
引理2.4 令x>0,s>0, 则有
证明记
由式 (4) , 引理2.3以及Cauchy-Schwarz定理得
再次运用Cauchy-Schwarz定理得
Os(d4),
综上所述,
Ud,x=Os(d).
引理得证.
引理2.5 令x>0,s>0则有
证明根据Rieger (文献[2], 引理8)知, 当d>0,s>0 时,有
记
由式 (4) , Rieger (文献[2], 引理8)以及Cauchy-Schwarz定理得
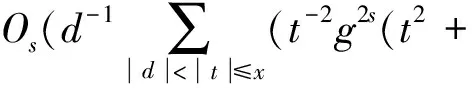
再次运用Cauchy-Schwarz定理得
d2))=Os(d-4),
综上所述,
引理得证.
2 定理1的证明
现在要找出S1,2(x)一个简单的界限, 已知0≤r2(n)≤r1(n)≤r0(n),运用Cauchy-Schwarz定理并结合式 (1) 、 (2) 可以得出
(5)
由r1(n),r2(n)以及S1,2(x)的定义知S1,2(x)表示(a1,p1,p2,p3)的个数, 其中
(6)
满足式 (6) 的(a1,p1,p2,p3)可以分为两类:一类为对角解, 即当{a1,p2}={p1,p3}时;另一类为非对角解, 即当{a1,p2}≠{p1,p3}时.
首先, 分离对角解跟非对角解, 则
其中:L(x)表示满足式 (6) 的(a1,p1,p2,p3)非对角解的个数.
下面证明,当x→∞时
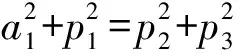
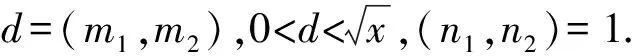
a1=tn1-dn2,p1=tn1+dn2,p2=tn2+dn1,p3=tn2-dn1.
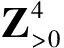
|t|≠|d|,tni±dnj∈P,i,j=1,2且j≠i.
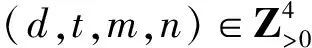
0<|dn|≤x,0<|tn|≤x, |m|<|n|,|t|≠|d|,n+dm,tm+dn∈P.
(7)
因此有
(8)
下面需要证明, 当x→∞时有
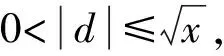
M(x)=M′(x)+M″(x).
(9)
下面计算M(x).
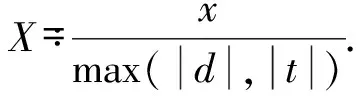
根据Brun筛法[15]以及式 (3) 得
通过式 (4) 以及引理2.1得
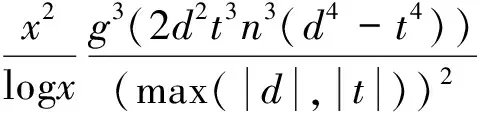
由引理2.4以及引理2.5得
再由引理2.2得
(10)
根据Brun筛法[15]以及式 (3) 得
通过式 (4) 以及引理2.4得
由引理2.1得
再由引理2.2得
(11)
把式 (10) 和式 (11) 代入式 (9) 得
根据式 (8) 得
综上所述,
S1,2(x)
定理1得证.

