高压重载螺旋传动副流固耦合与间隙优化分析

武恩林，权龙，乔舒斐

(太原理工大学新型传感器与智能控制教育部和山西省重点实验室，山西太原 030024)

0 前言

电动缸是一种新型的直线执行器，具有能效高、控制精度高等优势[1]，被广泛应用于多自由度模拟平台、航空航天等领域，但受限于伺服电机功率密度与螺旋传动副承载力，电动缸长期存在功率密度低、承载能力差等不足，难以应用于大功率重载场合。

国内很多学者在电动缸驱动力领域有一定研究进展。杨恺[2]改进了一种重载电动缸丝杠结构，使输出推力增大，并应用于1 MN电子万能试验机。焦让[3]开发了一种液压增力电动缸用于注塑机，使模具锁紧力增大5～7倍，但定位精度不足。LIU等[4]采用位置插值和改进的控制方法，提高了大型电动缸的承载力和稳定性，并将其应用于导弹发射器。郝云晓等[5-8]充分利用液压系统高功率密度和缓冲吸振的优势，在电机械直线执行器结构基础上，采用液压缸执行器的活塞与活塞杆替代与螺母连接的驱动杆，创新提出一种机电液混合驱动直线执行器，其中的螺旋传动机构通过高压油液对执行器进行助力，大幅提高了电机械执行器的承载力与功率密度。

螺旋传动副主要包括滚珠丝杠副、行星滚柱丝杠副和梯形丝杠副3种。行星滚柱丝杠副国内起步较晚，技术水平总体落后，价格昂贵[9]。滚珠丝杠副为点接触，承载力较弱，相同尺寸等级下梯形丝杠副具有更高的承载力[10]。因此，价格低、技术成熟、承载力大的梯形丝杠副是重载螺旋传动机构的首选。

目前已有很多学者开展了对梯形丝杠副(以下简称螺旋副)的研究工作。王文甲[11]利用有限元方法仿真研究了某型号电动缸中螺旋副在低摩擦因数以及冲击载荷下丝杠与螺母的应力和应变对零件承载性能的影响。程振锋、章争荣[12]基于静力学理论和有限元法针对传动螺旋副螺母上出现的应力分布不均和集中问题，提出了螺母结构的优化方案。在流场方面，EL-SAYED、KHATAN[13-14]提出一种采用非闭合环形面来代替螺纹侧面的螺旋副润滑油润滑等效模型，基于此模型分析了螺距、螺旋角、牙型角以及油腔占比等设计参数对螺旋副承载能力、流量、功率等的影响，并确定了各种参数的最优组合。卢佳佳[15]分析了在螺母偏移和倾斜影响下螺旋副的静动态特性变化。李松柏[16]研究了螺旋摆动液压缸中的螺旋副不同啮合间隙下的油膜压力、温度分布对间隙油膜润滑承载性能的影响。

近年来学者们对螺旋副做了很多有益的研究工作，但其在重载工况下，丝杠与螺母在高压状态的位移变形与油膜厚度属于同一量级，变形使间隙油膜厚度和压力分布不均匀，进而对螺旋副的工作状态、油膜润滑特性及承载能力产生一系列影响。因此，对高压重载螺旋副进行流固耦合分析，进行间隙油膜的承载特性以及丝杠螺母的变形研究有重要的现实意义。

本文作者针对机电液混合驱动直线执行器中的重载传动螺旋机构，采用流固耦合方法对流体压力和负载共同作用下螺旋副的应力和变形进行研究。研究中，首先对螺旋副进行结构分析，并对螺旋副及间隙油膜进行三维建模，通过有限元软件对流固耦合状态下的螺旋副进行强度校核，最后对间隙油膜的动压特性及润滑性能进行仿真研究。

1 重载螺旋传动机构工作原理

在电机械直线执行器的螺旋传动机构基础上，通过密封，将螺旋传动副的两侧构建为可充压力油液的容腔，提出如图1所示的液压重载螺旋传动机构。

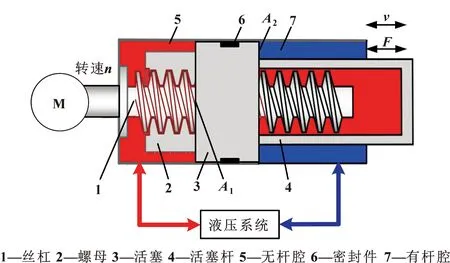
图1 重载螺旋传动机构

液压重载螺旋传动机构工作原理为：伺服电动机输出目标转速，经过螺旋传动副转换为推杆的直线运动。液压系统的高压油液通过执行机构两腔的有效作用面积A1、A2，实现力的放大作用，输出较大的力，提高螺旋传动机构的承载能力。同时螺旋传动副采用润滑油润滑，消除摩擦损耗，且螺旋副正常工作时丝杠与螺母啮合间隙变化形成的动压油膜具有承载和吸振性能。

根据上述分析，液压重载螺旋传动机构的运动控制方程为

v=nl/60

(1)

x=θl/(2π)

(2)

式中：v为传动机构直线速度；n为丝杠输入转速；l为螺旋副导程；x为传动机构位移；θ为丝杠输入转角。

液压重载螺旋传动机构驱动负载的动力学平衡方程为

(3)

式中：p1为无杆腔压力；A1为无杆腔有效作用面积；p2为有杆腔压力；A2为有杆腔有效作用面积；m为外负载质量；c为系统黏性阻尼系数；F为外负载力；Ff为包括摩擦力等的干扰力；T为传动机构输入扭矩。

根据式(3)知，在电机械驱动机构输出较小力的基础上，液压驱动机构输出较大的力，两者叠加共同克服外负载，提高了直线执行器的承载力，融合了液压直线执行器功率密度大、承载能力强的优点。

2 螺旋副流固耦合控制方程

螺旋副流固耦合分析是研究可变形的螺旋副在流场影响下的行为以及螺旋副变形对流场产生的反影响。对流固耦合的分析需要同时求解固体控制方程和流体控制方程。螺旋副间隙流体为螺旋面形状油膜，根据EL-SAYED、KHATAN[13]提出的等效方法，将螺纹螺旋面等效为如图2所示的非闭合环形面。

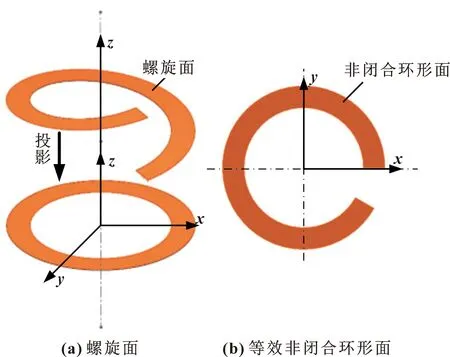
图2 螺旋面形状油膜展开图

2.1 流体域方程

质量守恒方程为

(4)

式中：ρ为油液密度；t为时间；v为油液速度；下标i，j=1，2，表示x、y两个方向的分量。

动量方程为

(5)

式中：p为流体压力；μ为动力黏度。

螺旋副间隙流体二维雷诺方程：

(6)

式中：u1、u2分别为x方向油膜上下两表面流速；w1、w2分别为y方向油膜上下两表面流速；h为油膜厚度；t为时间。

2.2 固体域方程

固体部分的守恒方程为

(7)

式中：Ms为单元刚度矩阵；Cs为单元阻尼矩阵；Ks为单元刚度矩阵；τs为固体单元受到的应力；d为固体单元的位移矢量。

2.3 流固耦合方程

流固耦合仿真分析中，耦合面处的数据交换应力τ、位移d等变量应满足相等或守恒原则：

τf·nf=τs·ns

(8)

df=ds

(9)

式中：n为耦合面的法线方向；τf、df分别为流体的应力、位移；τs、ds分别为固体的应力、位移，位移ds中增加了由流体压力引起的固体变形量。

由于丝杠与螺母的变形导致螺旋副间隙改变，进而引起油膜厚度发生变化，所产生的油膜动压力称为挤压效应。当螺母受到冲击载荷或振动情况下，由挤压效应所产生的油膜动压力对油膜承载起到很有利的缓冲减震作用。

本文作者选用直接耦合式解法进行求解，即建立控制方程的通用形式，在统一求解器中给定各参数以及对应的初始条件和边界条件，同时求解流体与固体控制方程以及流固耦合方程：

(10)

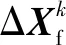
3 建模与边界条件

采用ANSYS Workbench进行流固耦合仿真，其中，螺旋副结构模型在Transient Structure模块中分析，油膜流体域在Fluent模块中分析，各模块间通过耦合器模块联接起来进行数据交换。

考虑到螺旋副实际运动的复杂性，在满足实际工况要求的基础上对仿真模型进行简化，引入如下理想化假设：(1)油膜的厚度方向压力为定值；(2)润滑油为理想牛顿流体，即油液不可压缩；(3)固体边界上的流体无速度滑移；(4)润滑油黏度不随温度变化；(5)油膜极薄，忽略惯性力和体积力作用；(6)无杆腔的油液压力与负载压力在螺旋副每对梯形齿均匀分布。

3.1 结构场模型与边界条件

利用三维软件对驱动系统部分螺旋副进行三维建模，螺旋副各参数见表1。为了更便于探究螺旋副间隙的流场，将其结构进行简化，忽略凹槽、凸台、密封圈、推杆等结构，其中间隙为0.20 mm的螺旋副结构如图3所示，简化后的结构以及丝杠与螺母啮合区域划分网格如图4所示。

表1 螺旋副参数

图3 螺旋副网格划分

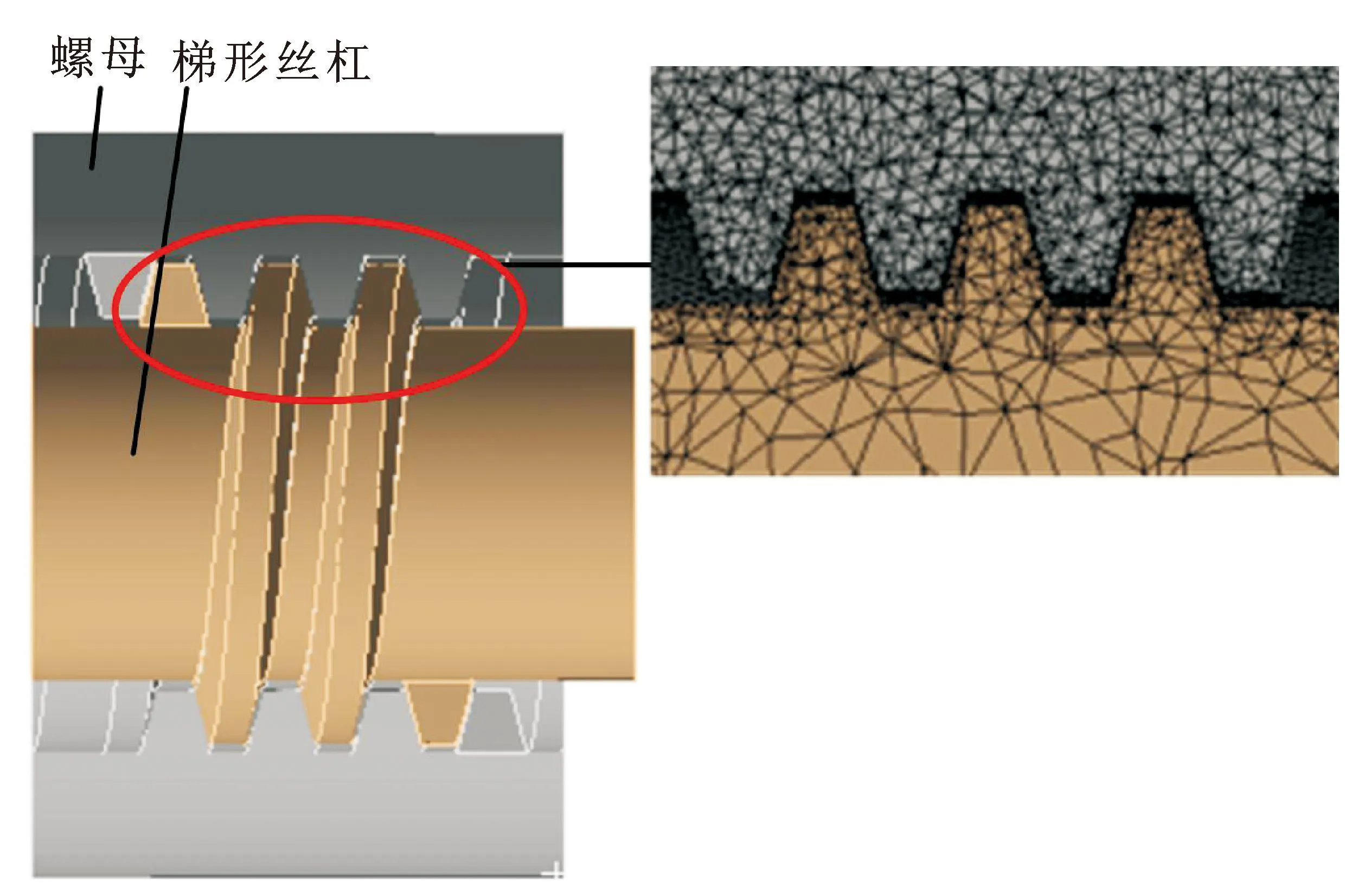
图4 螺旋副间隙结构

结构场模块中，在丝杠左端添加转动副来模拟丝杠的旋转运动，螺母添加水平移动副来模拟螺母相对丝杠的水平运动。接触面进行局部网格细化。结合具体工况，在螺母端面施加30 kN的推力模拟负载。定义丝杠与螺母的啮合面为流固耦合面。

重载螺旋传动机构承受重载时，丝杠与螺母在相对运动的过程中要承受较大的剪切应力和拉应力，因此选择丝杠材料为抗剪能力和抗拉能力较强的45CrNiMoVA，螺母材料为耐磨性能好的ZCuZn10Pb1。材料参数如表2所示。

表2 丝杠、螺母材料参数

3.2 间隙油膜流场建模和边界条件

为节省计算时间，重载螺旋传动机构内部耦合仿真的流体域由无杆腔、螺旋副间隙油膜两部分组成，其中螺旋副间隙油膜使用ANSYS Fluent前处理软件Design Modeler进行流场抽取。

网格划分时，间隙油膜的螺旋结构复杂，若采用结构类型网格进行划分收敛困难，因此网格类型选用非结构四面体，对与固体区域的耦合面进行局部网格细化，网格大小设为0.5 mm；对于压力等变化不大的区域，设置网格大小为1.0 mm，流场模型和螺旋副间隙内油膜的网格划分如图5所示。润滑油采用N46号抗磨液压油，材料参数如表3所示。

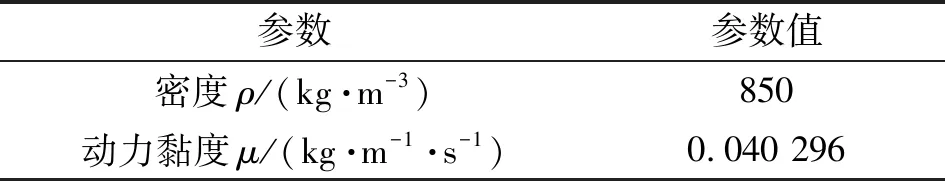
表3 液压油参数

图5 油膜流场网格

流体场模块中，腔内油液压力为实际工况下的20 MPa。动网格设置中，采用弹簧光顺网格更新方法和网格重构局部网格更新方法。由于流固耦合的仿真时间很短，所以仿真过程中没有考虑温度的影响。

4 仿真结果分析

4.1 油液压力对螺旋副间隙影响

丝杠与螺母受油液压力会发生形变，两者的径向变形会改变原有的配合间隙，造成间隙油膜厚度发生变化，进而对承载性能造成影响。因此首先分析油液压力对丝杠与螺母的径向变形量的影响，在无杆腔油液压力为20 MPa时，对螺旋副进行单向流固耦合仿真得到应变云图如图6所示。可知：丝杠与螺母在油液压力作用下会发生一定的变形，其中变形最大位置主要集中于前2-3个啮合齿圈，主要由于那一侧螺旋副承受油液压力。丝杠最大变形为7.7 μm，螺母最大变形为12.7 μm，导致螺旋副间隙减少量为5 μm。

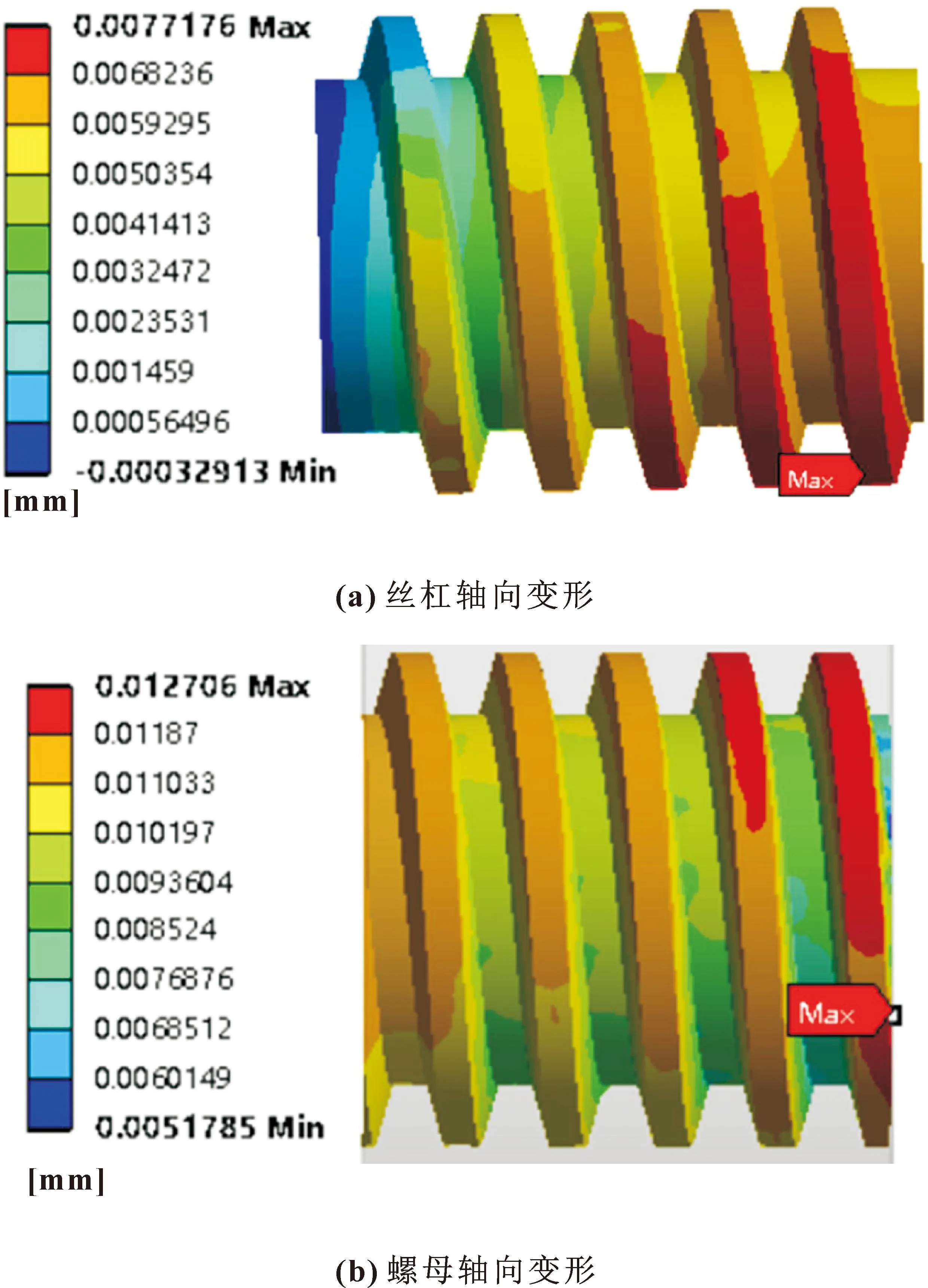
图6 单向流固耦合仿真分析螺旋副应变云图

为了更直观地分析在不同无杆腔油液压力时，丝杠与螺母的综合变形规律，根据其接触面轴向应变量画出相应的曲线，如图7所示。可以看出：随着油腔压力的增加，丝杠与螺母的轴向变形量最大值也随之变大；螺母的最大变形量始终大于丝杠的最大变形量，并且两者之间的差值随着压力的增加而增大，因此丝杠与螺母接触面间隙随着压力的增大而减小。在油腔最小工作压力时，间隙最大减少了4.5 μm，相当于初始间隙的5%，因此，油液压力对螺旋副间隙的影响不容忽视。

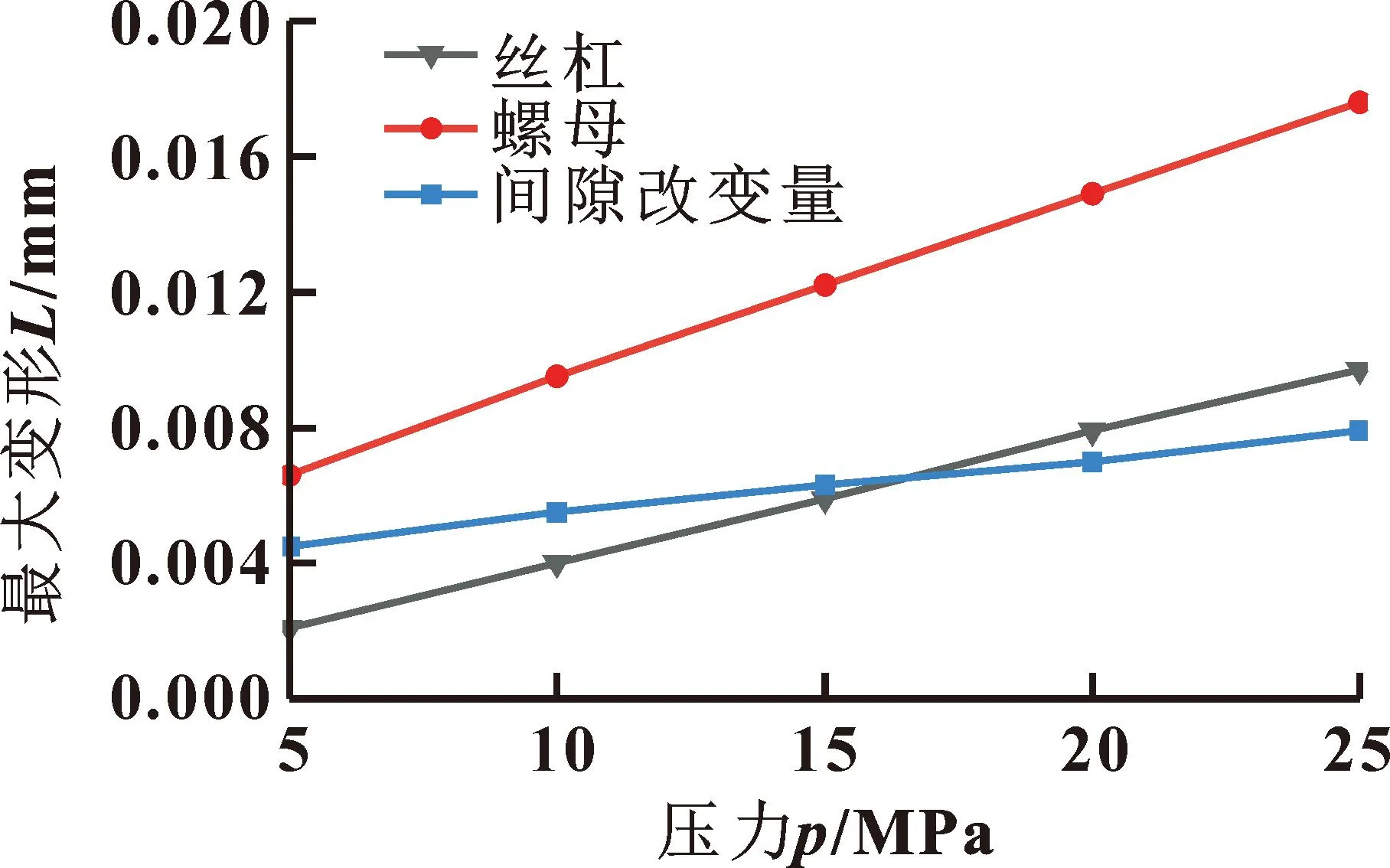
图7 丝杠与螺母接触面应变结果

4.2 螺旋副应力应变分析

螺旋副正常工作时承受负载，在负载和油液压力共同作用下对螺旋副进行双向流固耦合仿真，丝杠与螺母的应力云图如图8所示。由于双向流固耦合计算量较大，仅对螺旋副3个啮合齿圈进行分析。

图8 螺旋副应力云图

由图8可以看出：螺旋副螺纹根部应力集中比较严重，应力峰的最大值出现在螺纹齿圈和之间的螺纹凹槽处，沿着啮合方向越往螺旋副下端，螺纹凹槽中的应力峰值越小，显示出在螺旋副中沿啮合方向上端应力集中比较严重。丝杠在负载和油液压力耦合作用下的最大等效应力为260 MPa，螺母最大等效应力值为155 MPa。由以上应力仿真结果可知，丝杠与螺母在重载下均满足相应材料的屈服强度要求。丝杠与螺母的应变云图如图9所示。

图9 双向流固耦合仿真分析螺旋副应变云图

由图9可以看出：对比图6中螺旋副的应变量可知，在仅有油液压力无负载时的流固耦合形变量大于有负载时的形变量，这说明负载导致螺旋副变形的方向与油液压力所导致的变形方向不同，两者在一定程度上相互抵消，同时螺旋副接触间隙减小，间隙内油液被挤压产生动压效应。在流固耦合作用下，螺纹根部形变量最大，最大等效应变值为1 μm，占初始间隙的1%，因此对油膜厚度的影响忽略不计。

4.3 不同间隙油膜承载性能分析

考虑到间隙油膜厚度对承载性能的影响，分别建立间隙为0.08、0.10、0.15、0.20、0.25、0.30 mm的螺旋副模型。

对建立的6个不同间隙的螺旋副进行流固耦合仿真分析，在Fluent后处理模块观察仿真结果。厚度0.20 mm油膜动压效应云图如图10所示。随着间隙的增大，不同厚度油膜动压变化趋势如图11所示。

图10 厚度0.20 mm油膜动压云图

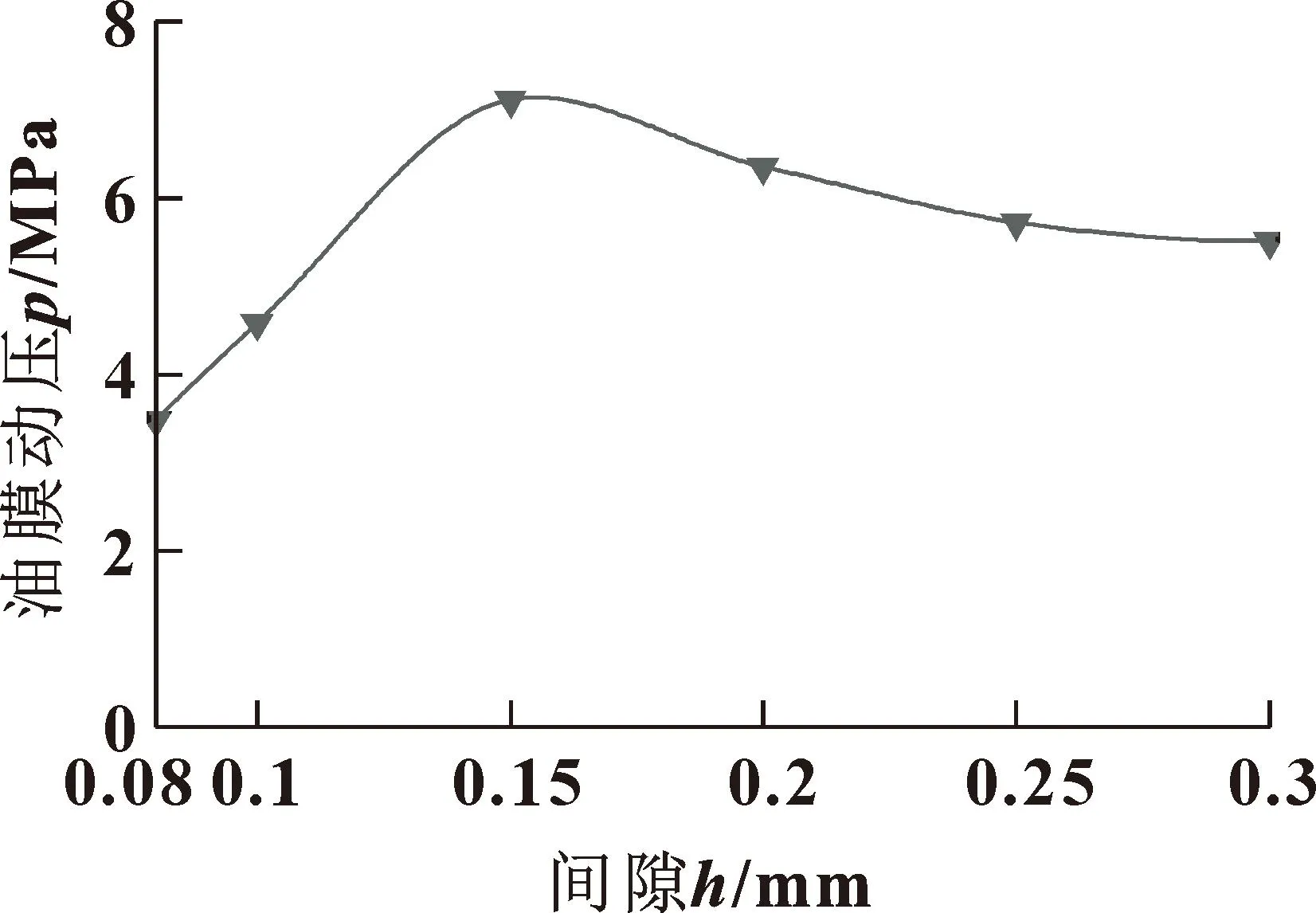
图11 不同间隙下油膜动压效应变化趋势

由图10、11可知：油膜在受到挤压后表现为螺旋齿两侧的压力不均衡，形成压力差，油膜螺旋齿两侧有明显压差。当间隙为0.15 mm时，动压压力达到最大，为7.31 MPa，表明螺旋副0.15 mm间隙时油膜的动压效果最好。

通过Fluent后处理模块中的Report-Force得到不同厚度油膜在仿真过程中的黏性阻尼力和液压油对流固耦合面的作用力矩M，通过Report-Surface Integrals积分得到液压油对流固耦合面的作用力F，根据得到的结果计算出刚度和摩擦因数，刚度K为作用力F与间隙h的比值，摩擦因数μ为黏性阻尼力f与作用力F的比值。6种不同间隙的仿真计算数据如表4所示，不同压力时油膜刚度以及作用力矩与间隙的变化关系如图12所示。

表4 不同间隙下油膜性能

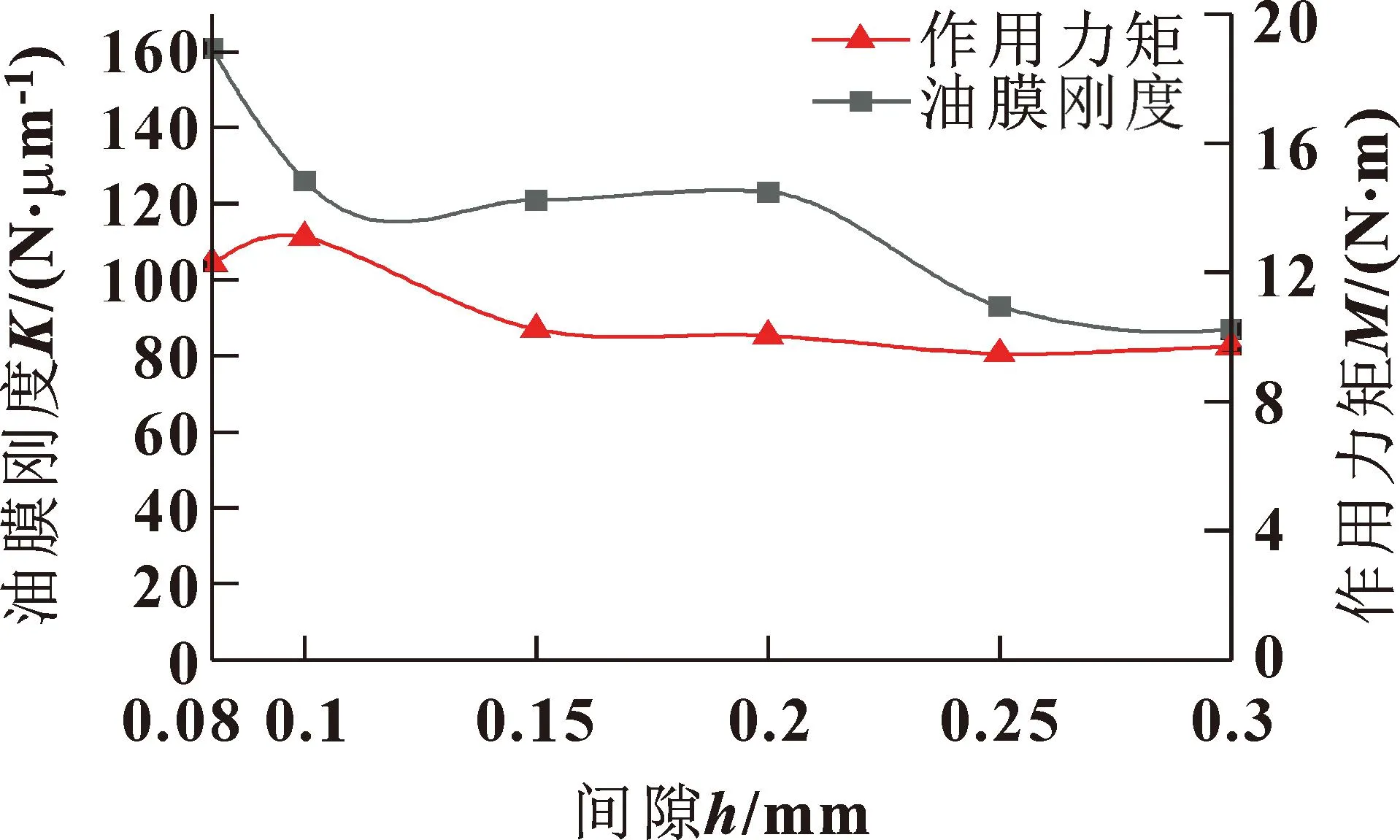
图12 间隙对油膜性能的影响

由表4和图12可以看出：5种不同的螺旋副间隙形成的油膜摩擦因数均只有0.002 5左右，表明润滑性能良好；油液对耦合面的作用力矩M随着间隙h的增大，呈现出先增大后减小的趋势，当h=0.1 mm时，油液对耦合面的作用力矩最大，可达13.08 N·m；当间隙增大到0.20 mm时，力矩减小较为缓慢；油膜刚度随着间隙h的增大呈现减小的趋势，当间隙增大到0.20 mm时，刚度减小较为缓慢，油膜的承载能力基本稳定。间隙过大，螺纹牙的强度下降，导致螺旋副承载性能下降；间隙过小，丝杠与螺母之间的运动会发生干摩擦和边界摩擦。综上所述，当间隙为0.15～0.20 mm时，螺旋副间隙油膜的润滑与承载性能最佳。

5 结论

通过对机电液混合驱动直线执行器中的重载传动螺旋机构采用流固耦合方法进行仿真分析，对梯形丝杠与螺母的应力应变和不同螺旋副间隙时油膜的润滑承载性能进行了分析，获得结论如下：

(1)在油腔压力作用时，丝杠与螺母的接触面间隙随着压差的增大而增大，最小油腔压力时的螺旋副间隙减少了4.5 μm，相当于初始间隙的5%，因此，流体压力对螺旋副变形的影响，即对间隙油膜厚度的影响不容忽视。

(2)在流体压力和负载共同作用下，螺旋副结构应力分布均匀，丝杠与螺母应力峰值出现在螺纹根部，分别为260、155 MPa，均满足相应材料的屈服强度要求；最大等效应变值为1 μm，占初始间隙的1%，因此对油膜厚度的影响忽略不计。

(3)螺旋副正常工作时，油膜受到挤压，表现为螺旋齿两侧油膜压力不均衡，形成动压效应，螺旋副间隙为0.15 mm时油膜的动压效果最好。

(4)5种不同的螺旋副间隙形成的油膜摩擦系数均只有0.002 5左右，表明润滑性能良好。综合考虑油液对流固耦合面作用力矩M以及油膜刚度的变化规律，当间隙为0.15～0.20 mm时，螺旋副间隙油膜的润滑与承载性能最佳。