大臂耦合运动串级PID复合控制方法研究

陈强，陈帅，徐受天，徐剑安，荆留杰

(中铁工程装备集团有限公司，河南郑州 450016)

0 前言

随着隧道施工智能化的不断推进，隧道施工专用设备也朝着智能化的方向不断发展[1]。采用智能化的施工装备可以降低人员劳动强度、减少施工人员数量、改善现场人员的作业环境和提高施工效率等[2]。在钻爆法施工中，智能型三臂凿岩台车具有智能化程度高、施工过程安全、作业效率快等优点[3]，因而在山岭隧道钻爆法施工中越来越受欢迎。液压机械臂作为智能型凿岩台车的末端执行器[4]，对整车的操控性能有着重要的影响，但台车的大臂采用下三角结构，把大臂俯仰和摆动两个运动耦合在一起，自动模式下的大臂运动控制成为一个难题，因此研究机械臂在自动模式下运动控制的稳定性、可靠性具有重要意义。

针对液压机械臂的控制，国内外很多公司和研究机构都进行了一定的研究工作。欧洲对智能型凿岩台车的研究起步较早，其中挪威的Bever Control公司所开发的凿岩台车大臂两个油缸分开单独控制，一个油缸控制大臂俯仰动作，另一个油缸控制大臂的摆动动作，结构上不存在耦合情况，控制相对简单[5]。

因液压机械臂控制系统本身是一个具有时变、强耦合的非线性系统，无法建立其完整准确的动力学模型，臂架的控制也比较复杂。覃艳明等[6-7]研究了单环位置环数字式PID控制器，通过Simulink建立阀控油缸液压仿真模型，但只是仿真测试了臂架的动态特性，并未测试阶跃响应等特性。目前有研究人员将PID控制与模糊逻辑、最优控制以及神经网络等智能化控制方案结合在一起，以实现对液压机械臂的准确控制，但实施过程较为复杂，削弱了PID控制的简单性，难以在实际工程中得到有效利用[8-10]。王千年等[11-13]研究了单神经元PID控制器和基于前馈补偿的PID控制器，只考虑了系统位置环误差，控制效果易出现抖动，关节控制误差为±0.18°，误差较大导致控制精度较低。谢天等人[14-15]采用机器学习算法，以控制系统输入输出的历史数据作为基础来完成对新的输入数据的预测，数学建模过程较为复杂，运算时间较长。在四旋翼无人机中，很多人采用了串级PID方法来提高控制系统的抗环境扰动能力，加快动态响应，但无人机为电控系统，电机响应速度比液压系统快很多，控制算法无法直接移植用于液压机械臂[16-17]。国内代表厂商铁建重工对隧道凿岩台车大臂控制采用专家PID控制，但这种控制基于专家的调试经验，原理虽然很简单，不易于表述，参数调试复杂，存在较大的应用局限性[18]。

本文作者首先对凿岩台车机械臂大臂结构和耦合运动原因进行详细表述，随后对所提出的凿岩台车大臂串级PID复合控制算法计算过程进行剖析，最后通过样机搭载测试验证算法的可行性，并对试验结果进行分析。

1 大臂结构模型

文中所研究的凿岩台车大臂结构简图如图1所示。

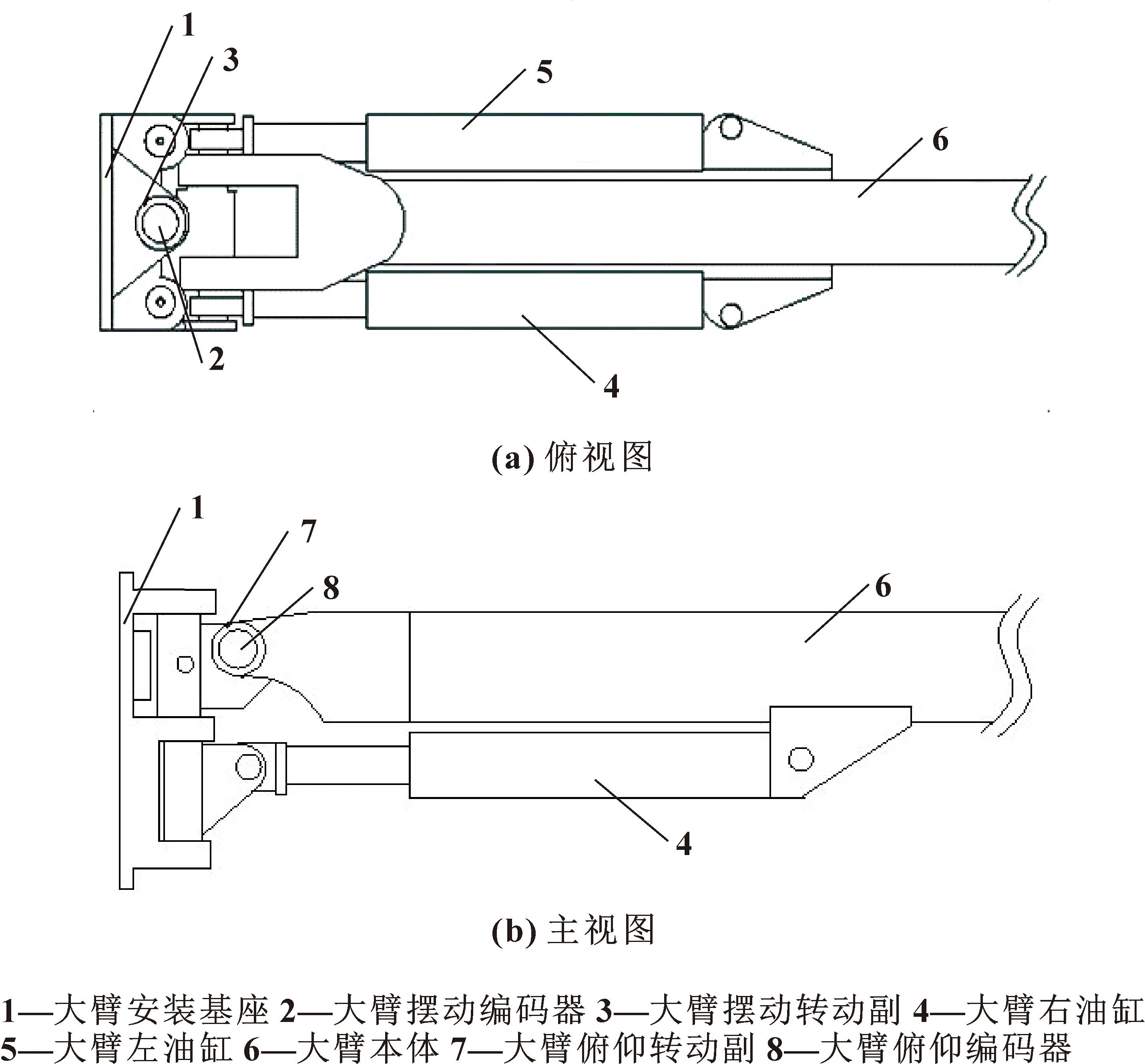
图1 凿岩台车大臂结构简图

凿岩台车的大臂采用两个油缸来控制大臂摆动和大臂俯仰两个关节的运动，若两个油缸同时伸缩，则可以控制大臂进行俯仰动作；若两个油缸一个伸出、一个缩回，可控制大臂进行左右摆动；因此大臂的运动方向与两个油缸的动作互相耦合在一起。其中，大臂俯仰关节、摆动关节上安装有绝对值编码器，可分别测量出两个关节的实时角度，通过两个关节的角度可推算出大臂左、右油缸的伸缩速度。

2 串级PID复合控制

智能型凿岩台车在自动模式下，各个关节会同时联动，以让机械臂末端尽快到达目标位置。因此，为了解决大臂耦合运动的难题，提出一种大臂耦合运动串级PID复合控制方法，以达到让大臂俯仰和大臂摆动两关节同时运动的效果。大臂的液压系统控制原理如图2所示，左比例阀、右比例阀分别控制大臂左油缸和大臂右油缸的伸缩运动；比例阀的开度可根据比例电磁铁的输入信号进行比例调节，阀开度调节范围为0%～100%。

图2 大臂液压系统控制原理

2.1 数字式PID

数字式PID控制算法主要包括两种：位置式PID和增量式PID，两者应用都很广泛[19]。

2.1.1 位置式PID控制器

位置式PID的输出值u(k)与过去所有的误差量有关，要对误差e(k)进行累加，适合液压系统的位置环精确控制，有输入误差时便能快速响应。把位置式PID作为串级PID复合控制的位置环，进行角度闭环控制。图3为位置式PID的控制框图。

图3 位置式PID的控制框图

位置式PID的递推原理如公式(1)所示：

e(k-1)]

(1)

式中：KP、KI、KD分别表示比例、积分、微分系数。

2.1.2 增量式PID控制器

增量式PID的输出值与最近3次的误差量有关，控制的是增量大小，可实现无扰动切换，适合用于液压系统的阀口开度控制，阀口开度变化平缓，运动速度过渡平滑，用在速度环利于控制系统的稳定。增量式PID作为串级PID复合控制的速度环。图4为增量式PID的控制框图。

图4 增量式PID的控制框图

增量式PID的递推原理如公式(2)所示：

Δu(k)=KP[e(k)-e(k-1)]+KIe(k)+

KD[e(k)-2e(k-1)+e(k+2)]

(2)

2.2 串级PID复合控制框图

本文作者设计了如图5所示的大臂耦合运动串级PID复合控制流程[20]。从左到右依次为大臂摆动和俯仰的目标角度、位置环PID、油缸速度复合运算、速度环PID、比例阀开度计算和编码器数据采集。

图5 串级PID复合控制框图

位置环为控制系统的外环，把大臂摆动和大臂俯仰的目标角度经过位置环PID分别输出左、右油缸的运动速度，经过速度复合运算得到左、右油缸设定目标速度；速度环为控制系统的内环，经过速度环PID分别输出控制左、右油缸运动的比例阀开度，比例阀驱动大臂左、右油缸运动使大臂摆动和俯仰两个关节进行转动。大臂摆动和俯仰关节的实时角度可通过绝对值编码器进行采集，利用编码器角度数据和大臂结构参数可计算出大臂左、右油缸的实际运动速度，从而实现串级PID的速度环和位置环的闭环控制。

2.3 串级PID复合控制算法

大臂摆动和俯仰的关节角度误差的计算公式(3)如下：

eθ1(k)=θ1-θ3

eθ2(k)=θ2-θ4

(3)

式中：θ1为第k次大臂摆动的目标角度；θ2为第k次大臂俯仰的目标角度；θ3为大臂摆动编码器的真实角度；θ4为大臂俯仰编码器的真实角度；eθ1(k)为第k次摆动关节角度的误差；eθ2(k)为第k次俯仰关节的角度误差。

当大臂摆动关节角度误差eθ1(k)输入到位置环PID，可输出得到的左油缸运动速度和右油缸运动速度计算公式(4)如下：

eθ1(k-1)]

vR1(k)=-vL1(k)

(4)

当大臂俯仰关节角度误差eθ2(k)输入到位置环PID，可输出得到的左油缸运动速度和右油缸运动速度计算公式(5)如下：

vR2(k)=vL2(k)

(5)

式中：vL1(k)、vR1(k)分别为第k次大臂摆动位置环PID输出的左油缸运动速度和右油缸运动速度；

vL2(k)、vR2(k)分别为第k次大臂俯仰位置环PID输出的左油缸运动速度和右油缸运动速度；eθ1(k-1)为第k-1次摆动关节的角度误差，eθ2(k-1)为第k-1次俯仰关节的角度误差；eθ1(i)为第i次摆动关节的角度误差，eθ2(i)为第i次俯仰关节的角度误差，i=0，1，…，k；KP1、KI1、KD1分别为位置环PID的比例调节系数、积分调节系数和微分调节系数。

大臂左、右油缸实际运动速度的计算公式(6)如下：

v′L=K′(θ3-θ3last)/Δt

v′R=K′(θ4-θ4last)/Δt

(6)

式中：K′为油缸结构三角关系计算系数；θ3为第k次大臂摆动编码器的实际数值；θ4为第k次大臂俯仰编码器的实际数值；θ3last为第k-1次大臂摆动编码器的实际数值；θ4last为第k-1次大臂俯仰编码器的实际数值；Δt为第k次与第k-1次大臂运动的时间差值。

大臂左、右油缸目标速度与实际速度的误差计算公式(7)为

evL(k)=vL-v′L

evR(k)=vR-v′R

(7)

式中：evL(k)为第k次左油缸的速度误差；evR(k)为第k次右油缸的速度误差。

通过速度环计算大臂左、右油缸比例阀开度增量公式(8)为

ΔdL(k)=KP2[evL(k)-evL(k-1)]+KI2evL(k)+KD2[evL(k)-2evL(k-1)+evL(k-2)]

ΔdR(k)=KP2[evR(k)-evR(k-1)]+KI2evR(k)+KD2[evR(k)-2evR(k-1)+evR(k-2)]

(8)

式中：ΔdL(k)为第k次左油缸的速度环PID输出的左油缸控制比例阀开度增量，ΔdR(k)为第k次右油缸的速度环PID输出的右油缸控制比例阀开度增量；evL(k-1)为第k-1次左油缸的速度误差，evL(k-2)为第k-2次左油缸的速度误差；evR(k)为第k次右油缸速度误差，evR(k-1)为第k-1次右油缸速度误差，evR(k-2)为第k-2次右油缸的速度误差；KP2、KI2、KD2分别为两个速度环PID的比例调节系数、积分调节系数和微分调节系数。

大臂左、右油缸的实际设定比例阀开度计算公式(9)如下：

dL(k)=ΔdL(k)+dL(k-1)

dR(k)=ΔdR(k)+dR(k-1)

(9)

式中：dL(k)和dR(k)分别为第k次控制大臂的左油缸和右油缸的比例阀开度；dL(k-1)和dR(k-1)分别为第k-1次控制大臂的左油缸和右油缸的比例阀开度。

以上为文中采用的大臂串级PID复合算法的具体推算过程，通过此算法最终输出控制大臂左、右油缸运动的比例阀开度值，从而实现控制大臂的耦合运动。

3 试验验证及结果分析

3.1 试验平台搭建

为了验证控制算法的可行性，搭建了智能型凿岩台车试验平台，此试验平台使用凿岩台车的一条液压机械臂进行测试。图6为试验平台的控制系统简图，其中：臂架系统为主控模块，在计算机内搭载大臂耦合运动串级PID复合控制程序；控制程序通过CAN总线可以与编码器和比例阀进行互相通信。

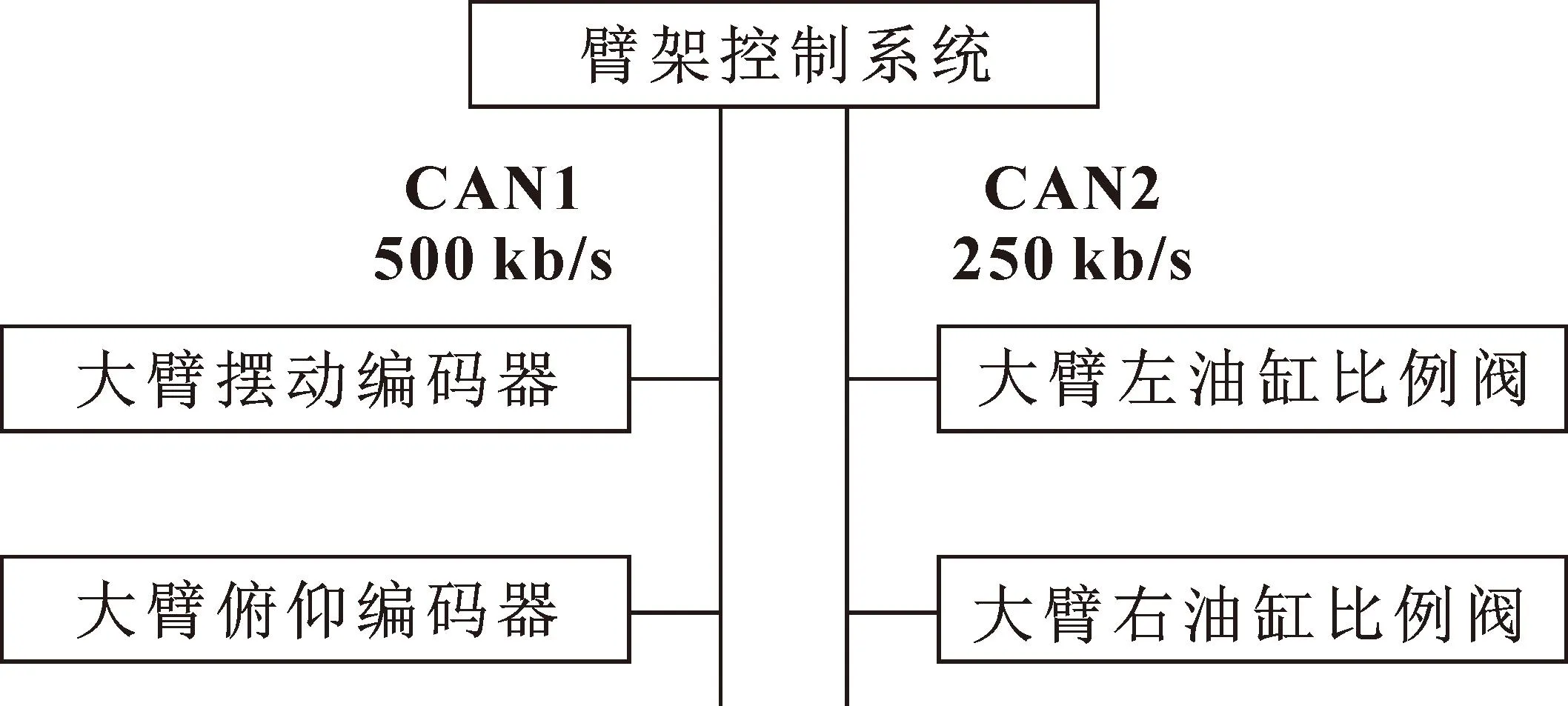
图6 试验平台控制系统简图

图7为现场试验图片，在大臂俯仰和摆动关节轴上分别装上绝对值编码器，对关节的角度进行实时采集，采集后的数据通过CAN1总线上传给控制程序，CAN1波特率为500 kb/s；控制程序利用串级PID复合控制算法计算出相应的比例阀开度，通过CAN2总线传输给比例阀，进而控制油缸的伸缩动作，CAN2波特率为250 kb/s。

图7 现场试验图片

3.2 试验测试及分析

在自动模式下对智能型凿岩台车进行试验测试，控制程序进行逆解运算后可得到大臂俯仰和摆动关节的目标角度，将大臂俯仰和摆动的目标角度输入串级PID复合控制算法。为了验证算法的稳定性，分别采用阶跃信号和斜坡信号来控制两个关节到达目标位置。图8为阶跃信号下大臂俯仰和摆动关节的实际运动曲线，图9为阶跃信号下大臂左、右油缸的运动速度曲线。

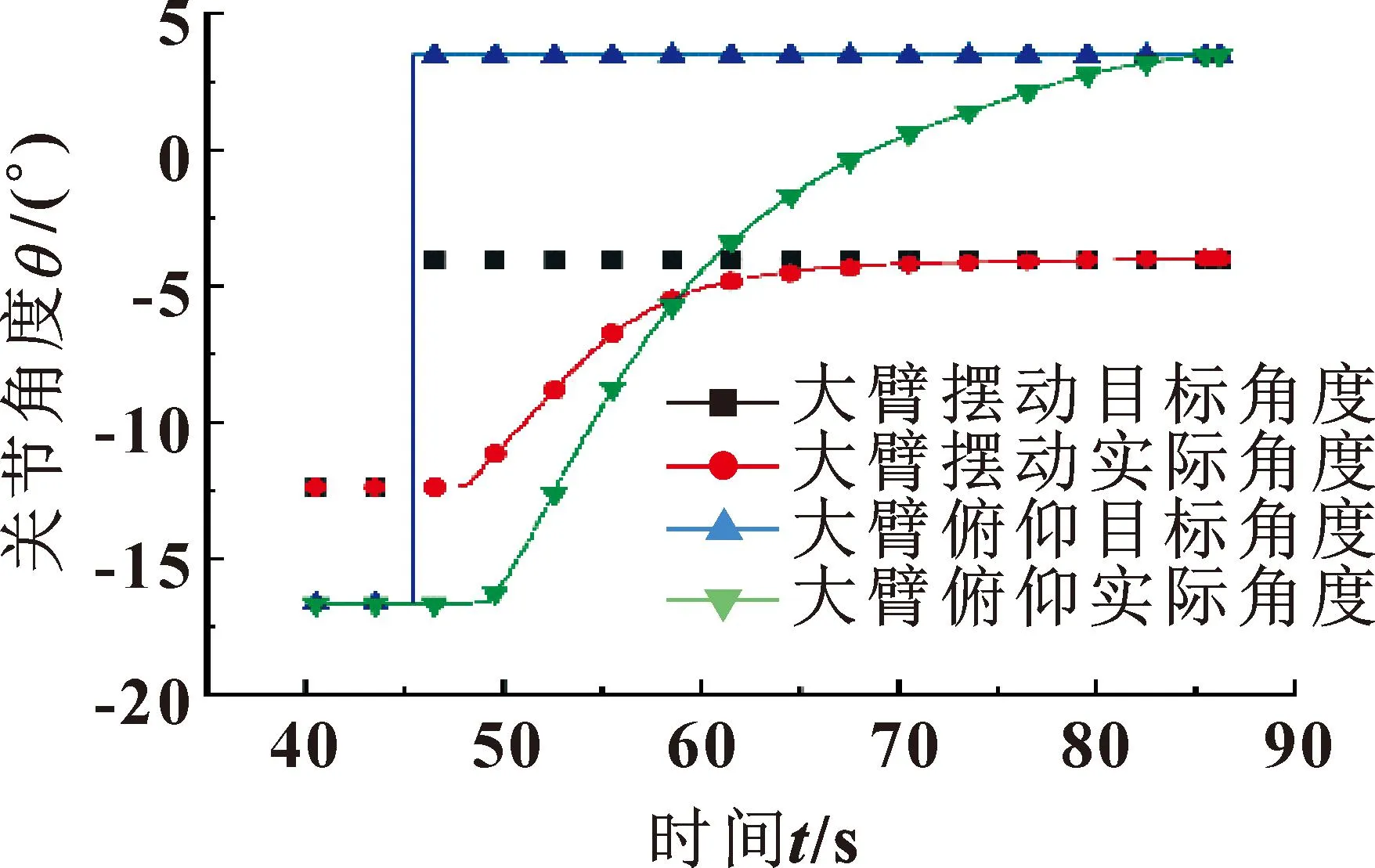
图8 阶跃信号下的关节角度曲线

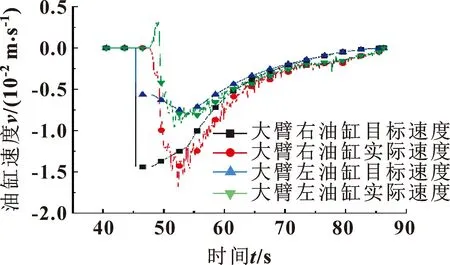
图9 阶跃信号下的油缸速度曲线

通过图8实际角度曲线可知：当阶跃信号下发后，大臂俯仰和摆动关节并没有立刻变化，延迟3 s左右。这是因为机械臂在不同的位置需要克服油缸静摩擦力和阀口死区，通过增大补偿死区和优化PID参数可以进一步提高响应速度。

图9中，左、右油缸的实际速度曲线在开始阶段也是为0 m/s，与图9中的开始段角度实际曲线无变化相对应。

当克服油缸摩擦力后左、右油缸开始同时运动，从图9可以看出左油缸的设定速度曲线与实际曲线基本重合，但实际曲线因外界干扰会有轻微的波动。从图9中的位置曲线看出：大臂俯仰和大臂摆动两个关节的实际角度曲线很平滑。从表1可知，在系统稳定后大臂摆动超调角度为0.042°，大臂俯仰位置环超调角度为0.031°，最大超调率仅为0.5%。这也说明了此串级PID复合控制算法虽然内环速度环受到一定的波动，但内环能够抵抗外界干扰，使外环保持稳定，提高了系统的稳定性。

表1 阶跃信号下关节目标角度与实际角度

在阶跃信号测试过程中，因大臂本身较重，且油缸运动速度较快，导致机械臂本身产生了一定的晃动。为了有效降低机械晃动，采用斜坡曲线让大臂俯仰、摆动两关节在运动过程中保持匀速运动。从图10中可以看出：大臂俯仰和摆动的目标角度曲线为一条斜率固定的直线，实际角度曲线在稳定段与目标角度曲线基本平行；实际角度曲线在开始段和结束段斜率出现逐渐变化的特点，这是由于油缸速度在开始段逐渐增大、结束段速度逐渐减小导致。斜坡信号稳定段角度误差如表2所示，在稳定段大臂摆动和俯仰的平均角度误差分别为3.78°和3.15°，最大波动率为15.87%，角度误差较小也表明了位置环跟随效果较好。

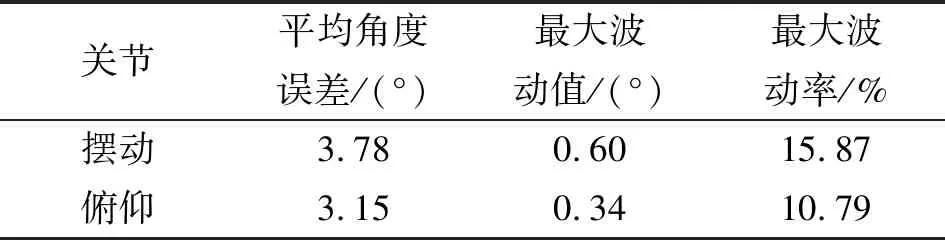
表2 斜坡信号稳定段角度误差变化

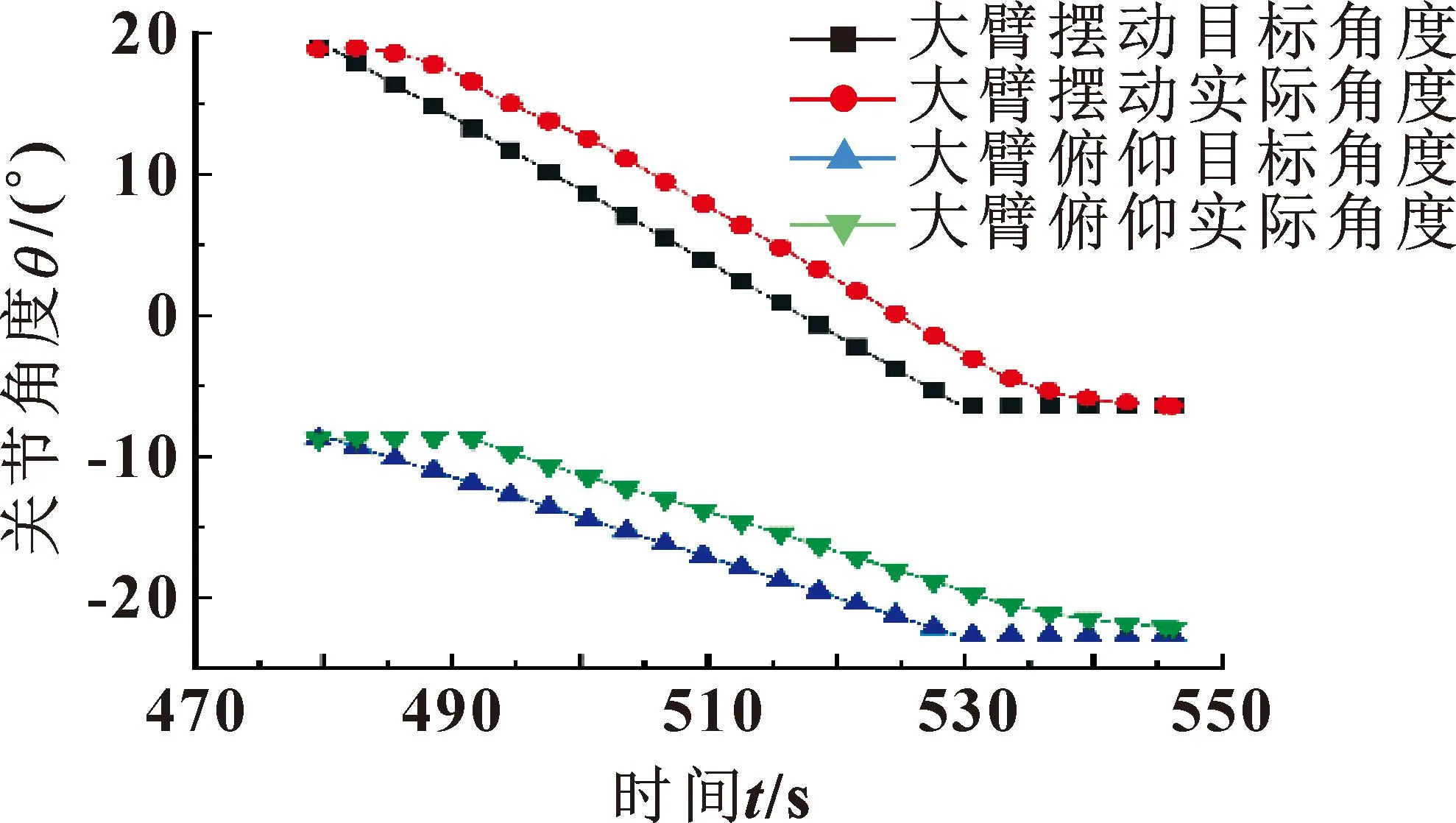
图10 斜坡信号下的关节角度曲线

通过图11的油缸速度曲线可知：在开始段和结束段速度变化较大，在中间稳定段左、右油缸的速度在一定范围内小幅波动，但基本保持稳定，与图10中的角度曲线刚好对应。在开始阶段由于大臂右油缸的目标速度由负值逐渐变为正值，速度方向切换导致开始段速度波动较大，并且大臂左、右油缸为刚性连接，右油缸速度波动会引起左油缸速度相应的波动，在稳定段左、右油缸的速度波动分别为0.001 5、0.000 1 m/s，最大波动幅度为37.5%。由于内环速度环是一个随动控制系统，可以有效地抑制干扰，降低对外环的影响，故在开始段角度曲线仍然平滑无抖动。

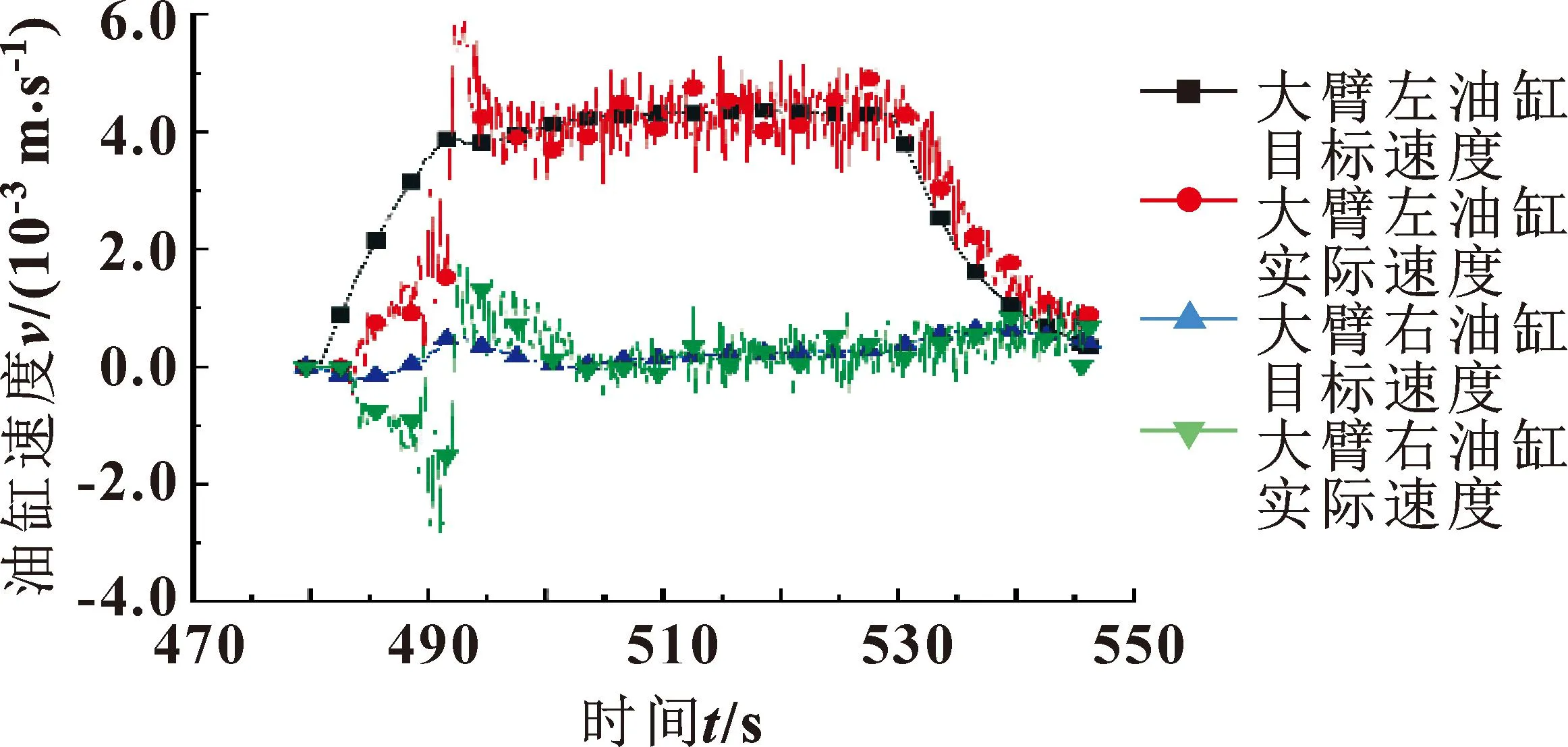
图11 斜坡信号下的油缸速度曲线

对比图9和图11可知：阶跃信号下的速度变化范围为0.015 m/s，斜坡信号下的速度变化范围为0.004 m/s，斜坡信号下的速度变化较小，臂架动作也更加平稳。

3.3 工程应用

在进行了试验测试后，所测试的智能型凿岩台车在云南昭通鲁甸隧道投入工程应用，如图12所示。现场经过3个月的施工作业，自动模式下的大臂俯仰和摆动关节动作流畅，运动过程稳定，现场应用效果良好。

图12 凿岩台车在隧道内的应用

4 结论

针对智能型凿岩台车在自动模式下大臂耦合运动无法控制的难题，提出一种大臂耦合运动串级PID复合控制方法，在位置环分解大臂俯仰和摆动关节动作，通过速度复合运算计算出大臂左、右油缸的目标速度，进入速度环分别控制相应的油缸动作，实现了大臂的耦合运动控制，并通过搭建试验平台进行了测试。

研究结果表明：

(1)所提出的串级PID复合控制方法能够有效解决大臂耦合运动的控制问题，外环回路是一个定值控制系统，内环回路是一个随动控制系统，外环回路不断纠正内环的设定值，使内环抵抗外界干扰，内、外环相互配合，保证了控制系统的稳定运行；

(2)所提控制方法的系统超调较小，阶跃信号下，内环采用增量式PID输出比例阀的开度增量值，阀口动作缓慢对系统冲击较小，最大超调量仅为0.5%；

(3)所提方法的动态跟随性能好，在斜坡信号下关节角度跟随误差稳定，速度变化范围只有0.004 m/s，从而降低了油缸速度的波动，跟随角度误差波动率最大为15.87%，在斜坡信号下大臂运动更为稳定。

由于速度环PID和位置环PID的控制参数中比例系数不够大，导致阶跃响应出现一定的延时。在后续的研究中作者将优化控制参数和增大比例阀死区补偿值，以进一步提高系统的动态响应速度。