活性粉末混凝土开孔梁受力性能研究

张爱社，曹照法

（山东建筑大学土木工程学院，山东 济南 250101）

0 引言

随着对建筑物使用功能的要求逐渐提高，与之相适应的各种辅助设施（供热、供电、通风、消防及给排水管道）系统也变得庞大而复杂。管线从梁底穿过，建筑物的层高也会随之增加。据调查，各种管线在梁下占据的高度约为层高的1／5 ～1／4［1］，利用梁腹开孔使各类管线在梁腹中穿行可以避免挤占梁下空间、减少层高，在层数不变的情况下可大幅降低建筑物的总高和自重［2］。

近年来，学者们针对开孔梁受力性能的研究做了大量工作。MANSUR 等［3］研究了洞口宽度、高度、位置等因素对开孔梁极限承载力的影响；SALAMA等［4］分析了T 形开孔梁在纯扭转作用下的受力性能；KENNEDY 等［5］通过对开有长方形孔的混凝土简支梁施加预应力，分析了混凝土梁的受力性能；DU等［6］开展了对开孔型钢-混凝土组合梁的抗弯性能研究；宋力等［7］采用物理试验方法探究了开孔水平位置对混凝土梁受弯承载力的影响；蔡健等［8］采用简支梁静载试验，通过改变开孔长度、高度等因素分析了预应力混凝土开孔梁的受剪性能。目前，开孔梁受力性能的研究对象大多为普通混凝土梁，但由于普通混凝土材料的脆性大、易开裂、抗压强度相对较低等缺点，孔洞的存在使梁截面刚度和承载力会受到较大削弱，而且孔洞周围存在应力集中现象，会使开孔位置成为梁的薄弱部位，如果处理不当很容易造成工程事故。活性粉末混凝土（Reactive Powder Concrete，RPC）通过优化颗粒级配使RPC内部达到最大密实度，采用高效减水剂以及成型时施压，降低了材料内部的孔隙率，通过高温养护加速火山灰反应并改善水化物形成的微结构，使RPC的抗压强度得到大幅提升［9-11］；钢纤维的掺入使材料的韧性及抗折强度得到了提升［12-13］，并且钢纤维的存在会对裂缝的扩展具有阻碍作用［14-15］。RPC的密实结构特点和组成有效地抑制了碳化，同时也具有很强的抗硫酸盐侵蚀能力，使材料具有良好的耐久性能［16-17］。RPC 良好的受力性能及耐久性，并在开孔梁受力性能方面优于普通混凝土开孔梁，使其逐步在桥梁、工业厂房、公共场馆等工程中得到广泛的运用。

为了探究RPC开孔梁的受力性能，文章应用有限元模拟软件中ABAQUS 的塑性损伤模型建立了一批RPC开孔梁模型，分析了开孔梁的受力性能，探讨了孔洞形状、大小、水平位置及竖向位置等孔洞参数对RPC开孔梁的极限承载力、变形以及延性的影响。

1 材料力学性能及本构模型

RPC材料和钢筋的力学性能参照了文献［18］中经试验测得的材料的力学性能，并选用其中部分试验梁结果来验证有限元模型建立的正确性。

1.1 材料力学性能

根据材料性能试验及理论计算，RPC 的轴心抗压强度fc为117.2 MPa、轴心抗拉强度ft为7.2 MPa、弹性模量Ec为4.1×104MPa。

RPC开孔梁纵向受力钢筋采用直径为25 mm的HRB500级高强钢筋，架力筋以及箍筋采用直径为8 mm的HRB400级钢筋。通过拉伸试验测得钢筋的屈服强度和极限强度，具体参数见表1。

表1 钢筋力学性能指标表 单位：MPa

1.2 材料本构模型

1.2.1 RPC的本构模型

根据RPC的配合比，选用文献［19］中所提出的活性粉末混凝土受压应力-应变本构关系，如图1所示，曲线的坐标系为无量纲坐标系，其中横坐标x＝ε／εc（ε、εc分别为混凝土应变和峰值应变）、纵坐标y＝σ／fc（σ为混凝土应力）。其本构方程由式（1）表示为

图1 RPC受压应力-应变关系曲线图

式中a、b为参数，且1 ≤a≤1.2、2 ≤b≤5。

1.2.2 钢筋的本构模型

钢筋的本构关系采用强化双折线模型，不考虑刚度退化。简化后的钢筋应力-应变曲线如图2所示。

图2 简化后的钢筋应力-应变曲线图

骨架曲线由弹性段（O-A）和强化段（A-B）组成，其应力-应变方程由式（2）表示为

式中σs为钢筋应力，kN；εs为钢筋应变；εy为钢筋屈服时的拉应变；εsu为钢筋极限拉应变。

2 开孔梁参数及有限元模型验证

2.1 开孔梁参数

以RPC矩形截面简支梁为研究对象，梁截面尺寸为180 mm×250 mm、梁全长为2 200 mm，加载时净跨为1 800 mm，跨中截面上部配有2 根直径为8 mm的架力筋，下部配有3根直径为25 mm的受力纵筋。RPC开孔梁的主要变化参数有：孔洞形状、直径、水平及竖向位置。为了使开孔因素的影响更加显著，孔洞周围不配置除箍筋外的加强筋。图3为RPC 开孔梁示意图（a为孔洞中心距支座的距离；p为荷载；e为孔洞中心与中和轴的距离，孔洞向上偏移时为正，反之为负）。各开孔梁参数见表2。

图3 LA-1梁截面尺寸及配筋示意图（单位：mm）

表2 梁试件开孔参数表

2.2 有限元模型验证

为了验证所建立的有限元模型的可靠性，对比不同梁的极限荷载有限元计算结果与文献［18］的试验结果，其结果见表3。两者间误差均＜5%，表明所建立的有限元模型是合理的。

表3 不同梁的极限荷载有限元计算结果与试验结果对比表

3 RPC开孔梁受力性能分析

3.1 开孔对梁承载力及变形的影响

3.1.1 开孔形状影响

在梁纯弯段内，LA-1（圆孔）、LA-2（矩形孔）、LA-3（方形孔）为开孔面积相同、孔型不同的RPC开孔梁。不同孔形对RPC开孔梁性能影响（破坏荷载为极限荷载的85%）如图4所示。从图4（a）的梁荷载-挠度曲线可以观察到，不同的开孔形式对实腹梁的极限承载力均有削弱，LA-0（实腹）的极限承载力为322.1 kN，LA-1、LA-2、LA-3 的极限承载力分别为317.8、315.6、309.5 kN，与实腹梁相比极限承载力分别下降了1.3%、2.0%、3.9%。对于开孔梁跨中横截面而言，圆孔梁、方形孔梁和矩形孔梁的孔洞高度分别为梁截面高度的48%、42%、30%，其中圆孔对跨中截面面积的削弱最大，而方形孔梁对梁极限承载力削弱最多。因为对梁截面开孔削弱了梁的整体性，易造成应力集中现象。相对于圆孔梁，方孔梁和矩形孔梁的孔角应力集中现象更显著，导致孔角处较早的出现裂缝，使RPC开孔梁的极限承载力有所下降。由图4（b）可知，在开孔面积一定时，圆孔梁的极限承载力相对于实腹梁削弱最小，方形孔削弱最大。总体来说，开孔面积相同、孔型不同的开孔梁之间的极限承载力相差不大。

图4 不同孔形对RPC开孔梁性能影响（破坏荷载为极限荷载的85%）

开孔对梁的变形也有一定影响，从梁荷载-挠度曲线上可以观察到，随着荷载增加，与实腹梁相比，在相同荷载下开孔梁的挠度值会有略微的增加。在开孔面积相同时，不同孔型的RPC开孔梁之间的变形相差很小。

3.1.2 孔洞直径影响

不同孔径对RPC 开孔梁性能影响如图5 所示。图5（a）为在梁纯弯段不同开孔直径下RPC梁的荷载-挠度曲线，随着孔径的不断增大，RPC 开孔梁的极限承载力不断下降。LB-1（直径为80 mm）、LB-2（直径为100 mm）、LB-3（直径为130 mm）、LB-4（直径为150 mm）、LB-5（直径为160 mm）的极限承载力分别为318.9、318.5、317.4、315.4、296.8 kN，相较于实腹梁其承载力分别削弱了0.96%、1.09%、1.43%、2.05%、7.83%。从图5（c）孔径对极限承载力的影响曲线中可以观察到：当梁开孔直径＜150 mm（0.6h，h为梁截面高度）时，开孔对梁的极限承载力的削弱很小；当开孔直径达到160 mm（0.64h）时，对梁的极限承载力的削弱变得十分明显。对于RPC梁来说，梁受弯极限承载力主要和纵向受拉钢筋与压区混凝土高度有关，当开孔不削弱压区混凝土时，开孔梁的正截面承载力较实腹梁相差不大。

图5 不同孔径对RPC开孔梁性能影响

LA-0梁的相对混凝土受压区高度约为0.224，而LB-1、LB-2、LB-3、LB-4 的开孔直径在80 ～150 mm（0.32h～0.60h）之间，并没有削弱RPC 梁的压区混凝土。由图5（b）可知，在相同荷载作用下，LB-1、LB-2、LB-3、LB-4孔洞上部混凝土的应力值相接近，孔洞周围没有明显的应力集中现象，开孔梁中的应力变化不明显，因此开孔梁的极限承载力基本一致。当开孔直径达到160 mm 时，孔洞上部已经进入混凝土的受压区。在相同荷载作用下，LB-5孔洞上部混凝土应力较大，孔洞上部出现较明显的应力集中，从而使开孔梁极限承载力下降，并且破坏时跨中的挠度会大幅度减小。对于RPC 开孔梁而言，在梁纯弯段开孔直径＜0.6h时，开孔对梁的极限承载力影响不显著；当开孔直径＞0.6h，开孔对梁的极限承载力的削弱会很严重。建议RPC 梁在纯弯段开孔时，尽量使其直径＜0.5h。从荷载挠度曲线上可以看出，RPC梁的变形随着开孔直径的增大而增大，表现为同一荷载下，随着孔径的增加开孔梁的挠度也会随之增加。

3.1.3 孔洞竖向位置的影响

孔洞竖向位置对RPC开孔梁性能影响如图6所示。图6（a）为孔洞竖向位置不同时RPC开孔梁的荷载-挠度曲线图。LC-1（孔洞中心下移10 mm，即0.04h）、LC-2（孔洞中心下移20 mm，即0.08h）、LC-3（孔洞中心位于中和轴）的极限承载力分别为314.5、316.9、317.2 kN，可以观察到，当孔洞从中和轴向下偏移时对梁的极限承载力影响不大。因为当孔洞向下偏移时，梁孔洞位于受拉区，孔洞周围没有明显的应力集中现象，梁中的应力基本上没有发生变化，从图6（b）孔洞上部混凝土的应力值可以观察到，在相同荷载作用下，孔洞上部混凝土的应力大致相同，孔洞周围无明显应力集中，所以梁的极限承载力不会产生较大变化。

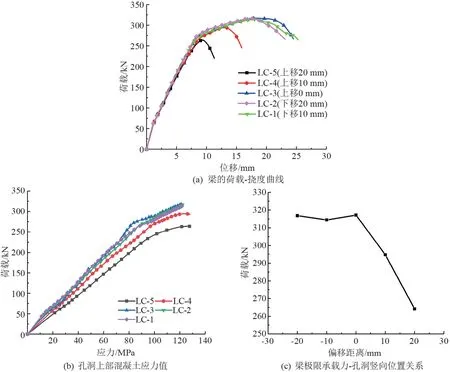
图6 孔洞竖向位置对RPC开孔梁性能影响

从荷载-挠度曲线中可以观察到，随着孔洞的位置向上偏移，对梁的极限承载力和挠度有着明显的影响。LC-4（孔洞中心上移10 mm）的极限承载力为294.8 kN，相对于实腹梁极限承载力削弱了8.4%；LC-5（孔洞中心上移20 mm）的极限承载力为264.2 kN，相对于实腹梁极限承载力减少了18%。如图6（b）所示，孔洞上移10 mm时，孔洞上部已经进入了混凝土的受压区，在相同荷载作用下，孔洞上部混凝土的应力值明显增大，孔洞上部区域出现较明显的应力集中，使开孔梁的破坏提前，导致开孔梁的极限承载力降低；孔洞上移20 mm 时，孔洞对梁受压区混凝土高度削弱已非常严重，孔洞上部应力集中现象较为突出，在相同荷载作用下，孔洞上部的混凝土的应力值增大十分显著，使开孔梁较早发生破坏，从而导致开孔梁极限承载力大幅降低。从梁的荷载-挠度曲线上可以观察到，开孔梁在达到极限承载力后随即发生破坏，破坏时跨中挠度不大，开孔梁没有明显的屈服段，属于脆性破坏。孔洞偏移位置对梁极限承载力的影响，如图6（c）所示，当孔洞向上偏移时，梁极限承载力出现了大幅度下降，表明孔洞位置向混凝土受压区偏移对梁受力性能极其不利，因此在实际工程中开孔位置要尽量偏向混凝土的受拉区，如果开孔必须向受压区偏移，需做好孔洞的加固措施。随着孔洞向上肢杆偏移，开孔梁的变形也会随之增大，表现为在同一荷载下，梁的跨中挠度增大。

3.1.4 孔洞水平位置的影响

孔洞水平位置对RPC 开孔梁性能影响如图7所示。孔洞在不同水平位置的荷载-挠度曲线如图7（a）所示，孔洞在纯弯段时，随着孔洞向加载点位置移动，RPC 开孔梁的极限承载力有小幅度减小，LB- 1、LD - 1 的极限承载力分别为318. 9 和312.2 kN。从图7（b）孔洞上部混凝土应力值可以看出，随着孔洞向加载点移动，在相同的荷载作用下，孔洞上部混凝土应力会有所增大，会提前压碎梁上部混凝土，导致开孔梁的极限承载力有所下降。

图7 孔洞水平位置对RPC开孔梁性能影响

开孔位置在弯剪段时，相较于纯弯段开孔梁的承载力和变形均产生很大的影响。开孔梁LD-2、LD-3、LD-4 的极限承载力分别下降到了287.6、303.4、302.2 kN，相较于实腹梁分别下降了10.7%、5.8%、6.2%。随着孔洞由纯弯段进入剪弯段，孔洞周围的受力情况由纯弯矩作用转变为弯剪共同作用的复杂应力状态，孔洞周围出现了明显的应力集中现象。孔侧箍筋的应变曲线如图7（c）所示，3 条曲线第一个明显拐点均为孔洞侧附近混凝土开裂时的荷载，第二个明显拐点均为孔侧箍筋屈服时所对应的荷载。当孔洞距离加载点较近时，孔洞便处在弯矩和剪力都较大的区域，孔侧会产生较大的应力集中，使孔侧箍筋较早屈服，孔角的裂缝会快速向加载点扩展，导致梁承载力的下降；当孔洞远离加载点时，虽然孔侧的应力集中现象有所减弱，但是在孔洞附近会产生较多的腹剪斜裂缝，使开孔梁的极限承载力下降。图7（d）为孔洞水平位置对梁极限承载能力的影响曲线，开孔位置设置在梁弯剪段时，开孔梁的极限承载力会有明显削弱。而且随着孔洞位置移到弯剪段，开孔梁的变形也明显增大，表现在同一荷载下，开孔梁挠度值有所增大，当荷载达到285 kN时，LB-1、LD-4的挠度值分别为9.86、12.20 mm，而LD-2、LD-3 的挠度值分别增大至14.40和13.00 mm。

3.2 开孔对RPC开孔梁延性性能的影响

延性系数是在钢构件和钢筋混凝土构件的受力性能基础上建立的，为极限变形与屈服变形之比［20-22］，即μ＝Δu／Δy，其中μ为位移延性系数；Δy为梁屈服时的位移，取纵向受拉钢筋屈服时的挠度，mm；Δu为极限挠度，取试件所加荷载下降至峰值荷载的85%时对应的梁跨中挠度，mm。各试件的位移延性系数见表4。不同开孔参数对RPC开孔梁延性系数的影响如图8所示。

图8 不同开孔参数对RPC开孔梁延性系数的影响

表4 不同孔型RPC梁的位移延性系数表

由表4和图8可知：

（1）不同形式的开孔使RPC 实腹梁延性有一定程度地降低。在开孔面积相同时，矩形孔RPC开孔梁所表现出的延性最好，而圆形孔RPC开孔梁的延性相对较差。

（2）孔洞位于纯弯段时，对于开圆形孔的RPC开孔梁，其延性系数随着开孔直径的增加而逐渐减小。当开孔直径小于梁截面高度的50%时，开孔梁的延性系数下降的速率相对较缓；当开孔直径大于梁截面高度的50%时，开孔梁的延性系数会随着开孔直径的增加而迅速减小。这表明对于圆形孔RPC开孔梁，当孔径不超过截面高度的50%时，随着开孔直径的增加，开孔梁的延性会随着孔径的增大而缓慢下降。但是当开孔直径超过梁截面高度的50%时，开孔梁的延性会随着开孔直径的增大而迅速降低。

（3）对于开孔位置在纯弯段的RPC开孔梁，随着开孔位置向下偏移，RPC 开孔梁的延性系数会有所增大。当开孔位置向上偏移时，开孔梁延性系数会迅速降低。由此可见，对于开孔位置位于纯弯段的RPC开孔梁，当孔洞位置向下肢杆偏移时，RPC开孔梁的延性会有所增加，但是当孔洞位置向上肢杆偏移时，开孔梁的延性会受到严重削弱。

（4）位于纯弯段的开孔梁LB-1、LD-4，随着孔洞位置向加载点移动，RPC 开孔梁的延性系数会有所下降。位于弯剪段的开孔梁LD-1、LD-2、LD-3，随着孔洞位置向加载点靠近，开孔梁的延性系数呈现出先增加后减小的趋势。与纯弯段开孔梁相比，弯剪段开孔梁的延性系数明显降低。这表明在梁纯弯段内，孔洞水平位置的移动对开孔梁的延性影响较小。但是当孔洞位置移动到梁弯剪段内时，开孔梁延性会大幅下降，在靠近加载点处影响最严重。

3.3 开孔梁正截面承载力近似计算

对于RPC开孔梁，当开孔没有削弱压区混凝土的面积，即梁的受压区边缘至孔口的距离大于实际受压区高度，此时可忽略孔洞对梁正截面承载力的影响。由于RPC有较高的抗压强度，RPC梁的受压区高度相对较小，当开孔直径小于截面高度的50%时，基本上不会削弱压区混凝土的面积，可按照实腹梁的计算公式来验算正截面承载力。RPC 的抗拉强度约为普通混凝土的10倍，不能忽略受拉区RPC的拉力对截面承载力的贡献，因此在正截面承载力计算时应该考虑RPC 拉力的贡献。RPC 梁的正截面承载力由文献［23］中所给的公式进行估算，由式（3）和（4）表示为

式中Mu为梁正截面受弯承载力，kN·m；h为梁截面高度，mm；h0为梁截面有效高度，mm；b′为梁截面宽度，mm；As为纵筋截面面积，mm2；as为受拉钢筋合力点到梁受拉边缘的距离，mm；x′为等效受压区高度，mm。

把梁参数带入式（3）和（4）计算得出梁承载理论值Mu，c，并与模拟值Mu，s比较，其结果见表5。梁的正截面受弯承载力计算值与模拟值较为接近，并有一定安全储备。由表5 数据计算得出，Mu，c／Mu，s均值为0.943、标准差为0.006 3、变异系数为0.006 7，由此可知，梁正截面受弯承载力计算值与模拟值较为吻合。

表5 梁正截面受弯承载力计算值和模拟值对比表

4 结论

通过对18根RPC 开孔梁的有限元仿真分析，探讨了孔洞形状、大小和位置的变化对开孔梁受力性能的影响，主要得出以下结论：

（1）在开孔面积相同情况下，不同开孔形式的RPC开孔梁在极限承载力、变形以及延性方面变化不明显。圆孔梁在极限承载力方面要优于矩形孔梁和方形孔梁，但在延性方面要稍差。

（2）在纯弯段开孔时，开孔梁的极限承载力及延性会随着开孔直径的增加而减小，变形随着孔径的增大而增大。当开孔直径达到截面高度的60%时，对开孔梁极限承载力的影响不明显，但开孔梁的延性会有很明显的降低。在RPC梁纯弯段开孔时，开孔直径要控制在梁截面高度的50%以内，建议实际工程中开孔梁正截面承载力设计可按照实腹梁的计算公式进行计算。

（3）在纯弯段，随着孔洞位置向混凝土受压区偏移，孔洞上部出现明显的应力集中现象，对开孔梁的极限承载能力及延性均有较大程度的削弱，使开孔梁变形增大。因此，RPC 梁开孔，要尽量避免孔洞向受压区偏移。

（4）孔洞在纯弯段时，随着孔洞水平位置向加载点移动，开孔梁的极限承载力及延性会有所下降。当开孔的水平位置位于弯剪段时，开孔梁在承载力以及刚度方面会有较为明显的下降。因此，建议开孔位置应尽量布置在梁纯弯段靠近跨中的位置。对于要布置在梁弯剪段的孔洞，应避免布置在靠近加载点的位置。