基于GN-PR的重要节点挖掘算法研究

王笑颜，陈伯伦，许 雪，王 凌，刘晓娈，王珊珊

（淮阴工学院 计算机与软件工程学院,江苏 淮安 223003）

在自然界和社会中,许多复杂的系统都可以用网络和图来描述,在复杂网络中挖掘关键节点作为其主要研究方向,目的是为了发现在网络结构和信息传递过程中起着重要作用的节点［1］。当出现新思想或新行为时,人们对新事物的接受程度受到周围人的影响,这些新事物可能很快消亡,也可能形成广泛深入的影响,这与影响该行为的关键传播节点的影响力有直接关系［2］。因此在复杂网络的研究和实践中分析网络中各节点的重要性进而挖掘关键节点具有重要意义。在网络影响力传播的过程中,具有影响力的节点也就是重要节点,指的是能够引发信息进行广泛的传播或阻止扩散的节点。影响力最大化是从复杂网络中确定一小组有影响的节点,以最大化激活节点的数量。由于选择种子节点的准确性、稳定性和时间复杂度等关键问题,近十年来出现的大多数影响力最大化算法都遇到了挑战,例如缺乏最佳种子节点选择,不合适的影响力传播和高时间复杂度［3］。

目前许多学者正对网络中重要节点的挖掘展开研究,Liu 等［4］提出了一种基于改进结构洞和K壳分解算法的重要节点识别算法,用于识别复杂网络中影响安全的重要节点,并且在考虑网络的全局结构的基础上,提出了一个基于节点度和最近邻域信息的无网络组织先验知识的重要节点的网络安全评价指标。陈文杰等［5］提出一种基于节点向量表示的模糊社区划分算法,该方法由节点重要性引导的随机游走策略生成节点序列,通过最大化模块度得到最佳的社区数目。对于PageRank方法结果过于集中,未考虑复杂网络社区结构特性的问题,王安等［6］提出了一种基于复杂网络社区划分的节点重要性排序方法CD-PR,将社区的内外连接关系转化为社区选择的概率表示,得到关键节点排序结果。从社区结构上来看,郑黎黎等［7］采用分裂算法中的GN 算法,提出道路交通网络模块度函数实现路网区域划分。Jing 等［8］研究了目标影响最大化问题,提出了一种基于索引的MSTIM 问题求解方法,实现了MSTIM 的高效求解。目前,经典的社区划分算法已经不能满足需要,因此本文采用改进的社区划分算法挖掘重要节点,旨在提高节点的传播效率。

过去的若干年中,学者都在节点特征的基础上进行关于重要节点的挖掘,却忽略了节点之间的重叠影响力。本文针对此问题在使用GN 方法进行社区划分的基础上,提出了社区重要性的概念并对节点进行识别和排序,同时也考虑了边的差异和节点的PR 值对节点排序的影响。为了评估该算法是否有效,我们应用独立级联（Independent Cascade Model,IC）模型模拟了真实网络中的扩散过程,通过实验对节选出的节点传播能力进行测评。实验结果表明,该方法节选出的节点传播效率较高,在控制节点的传播方面具备较好的优势,在识别传播能力强的节点方面比其他方法更加有效。

1 算法描述

本文对复杂网络中节点的挖掘问题用图的结构来进行模拟,提出了一种改进的网络重要节点挖掘算法GN-PR（Girvan Newman and PageRank,GN-PR）,该算法首先通过GN 算法对图进行社区划分,其次从每个社区内部计算节点的PR 值,接下来将PR值最大的节点选为首位节点,最后按照社区的重要程度对节点进行排序输出。算法的流程如图1所示。

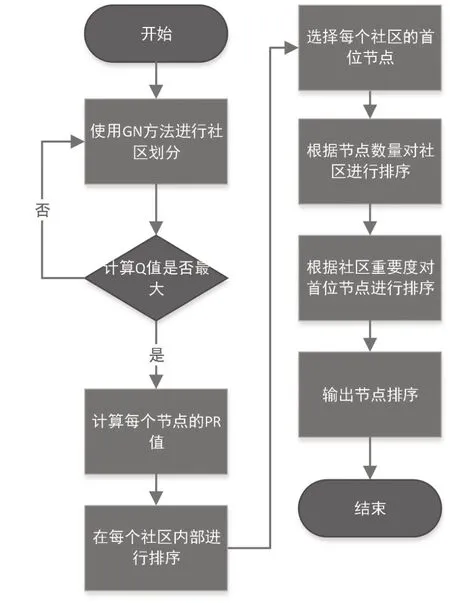
图1 算法流程图

1.1 详细描述

1.1.1 基于GN算法的社区划分

本文选用的GN 算法是基于边介数的方法。某边的边介数的定义是网络中全部节点间的最短路径经过该边的次数。网络中有社团内部关系比较紧凑、社团之间关系比较疏松的特点,根据这个特点来逐次删除社团之间的边,获得关系比较紧凑的社团结构［7］。GN算法的根源就是基于这种思想,逐次删掉边介数最大的边,直至完全淘汰全部的边,最终在特定的模块度条件下,取得效果最优的网络社区结构。Girvan和Newman提出模块度Q的概念的目的是为了描述社区划分的成功程度,能够对社区模块化地进行描述。对一个能够表示为n×n矩阵的无向网络,对Q函数模块化如下：

其中,i 表示第i 个社区,eii 代表社区i 的边占最初网络全部边的比例,ai代表全部将社区i中的顶点连接起来的边占总边数的比例。

经过持续的迭代运算,得到模块度最大的情 况并完成社区划分（见表1）。

表1 社区划分步骤

1.1.2 使用PageRank算法进行社区内部节点的排序

PageRank算法属于图数据上的无监督学习方法。Google 公司首先提出了网页重要性的排序算法——PageRank 算法,算法主要根据网页之间的超链接关系对网页的重要程度进行评估。本文中的节点指的是概念中的网页,边指的是网页间的超链接,则PageRank 算法是指有向网络中在对节点重要性进行评价的基础上挖掘这之中的关键节点。计算公式为：

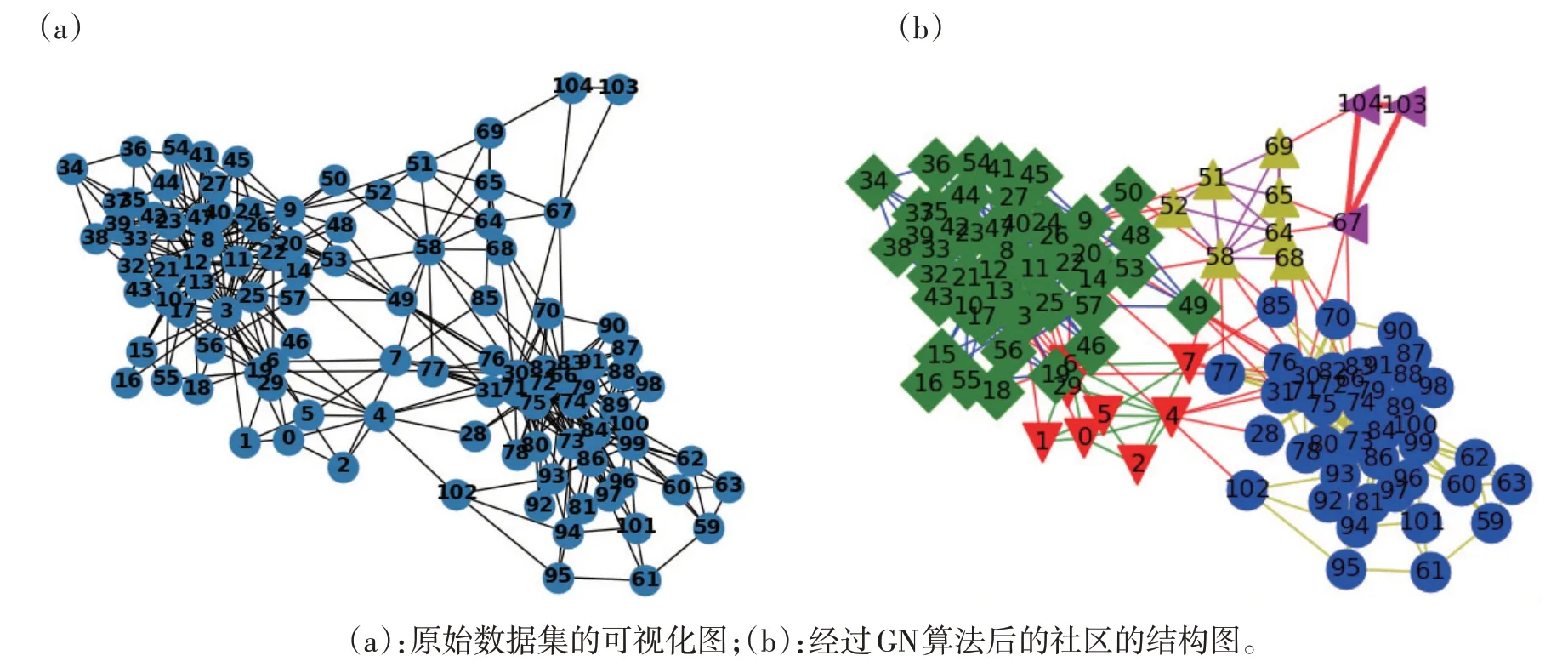
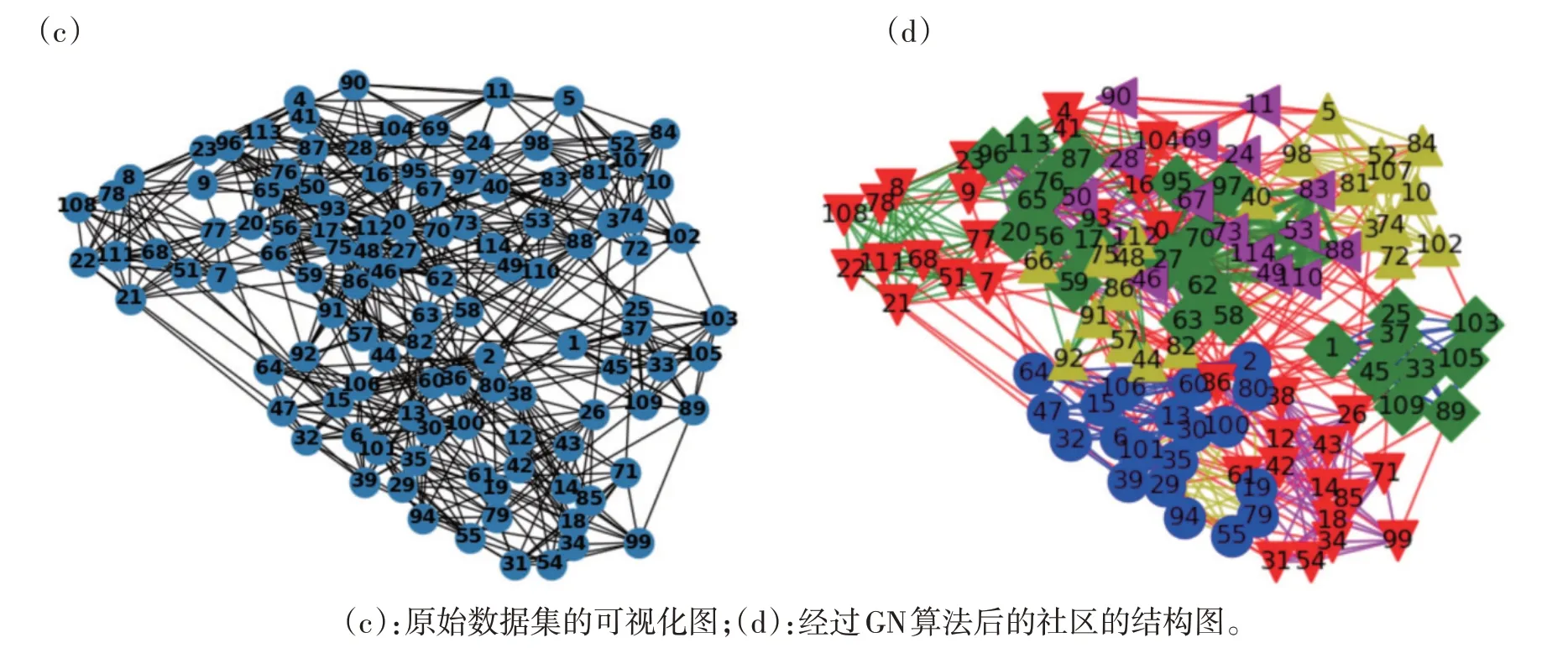
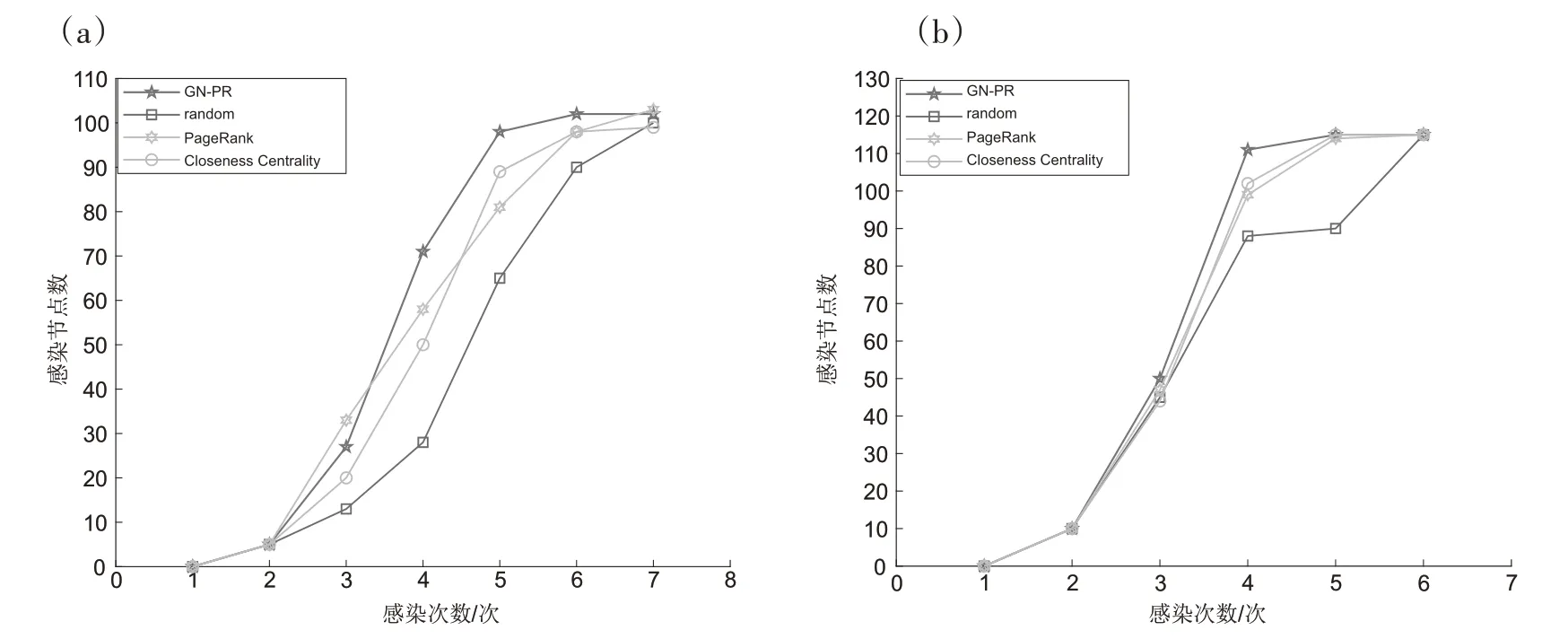
DPR（i）为节点i 的PageRank 值,d 为阻尼因子,0

PageRank 是递归定义的,PageRank 可由迭代算法进行计算,PR 值必须经由多次循环迭代才能达到一个稳定值。如果某节点与其它节点之间没有出链,这就是Spider Traps,这将导致节点偏移（经过多轮迭代后,没有出链的节点的权重越来越大,趋近于1）,需要对M进行修正：

其中β表示跟随出链打开节点的概率；1-β表示随机转到其他节点的概率；eeT表示由1 填满的n×n矩阵。

计算每个节点的PageRank值并按从大到小的顺序排序,选择每个社区内PR 值最大的节点（见表2）。

1.1.3 根据社区重要性进行节点的挖掘

根据社区内节点数量进行社区重要性评估,每个社区的种子节点数量集合跟社区的重要性成正比,社区内的种子节点数越多,说明本社区的重要性越大。最后将每个社区中PR 值最大的节点再根据社区的重要性进行从大到小的顺序排序输出,得到最终的节点序列（见表3）。

表3 社区重要性算法步骤

1.2 影响力传播模型

独立级联IC 模型（Independent Cascade Model）最初为一个概率模型。在IC模型中的信息扩散过程如下：

1）当节点u在t时刻被激活后,在最初的活跃节点集合A 中,节点u 就可以产生一次对u 的邻居节点w作出影响的机会,成功的概率是pu,w,其为随机赋予的参数,其他节点对它产生不了影响,参数值越大,节点w被影响的概率越大。

2）如果新被激活的节点都是w 的邻居节点,那这些节点会以随机次序尝试激活节点w。若节点u 把节点w 激活,则节点w 可以在t+1 时刻变成活跃状态。

3）当处于t+1时刻,其他节点将会被w影响,重复上述过程。

在上述传播中,不管节点u 的邻居节点在t 时刻是否能被激活,在之后的过程中,u 本身即使一直是活跃状态,但也不再有影响力,没有任何影响力的活跃节点就是指这类节点。当网络中不再有具备影响力的活跃节点时,结束传播。

1.3 影响力传播评价指标

在影响力的传播过程中,需要选取传播能力较高的节点集合,这样可以在有限的成本下最大化的完成节点的传播。本文设计了选择重要节点的有效方法,为了评估节点的传播能力,我们将感染的节点数量与迭代次数的比值定义为传播效率,计算公式为：

其中Eff表示节点的传播效率,vol为感染的节点总数量,N为迭代的次数。

2 结果与分析

2.1 实验环境及数据集

算法使用的开发语言为python,利用python中的networkx 编程语言软件包对复杂网络进行创建和操作。在Windows10系统上进行训练和测试,硬件环境为i7-1165G7 CPU @2.80GHz、NVIDIA GeForce GTX 1650 Ti with Max-Q Design,显卡的共享内存为16G,能够满足深度学习的最低要求。

实验采用了两个公共数据集,分别为polbooks数据集和football 数据集。polbooks 数据集,是由V.Krebs从Amazon上销售的美国政治相关书籍页面上建立起来的网络［9］。该数据集中包含105 个点和441 条边,其中每一个节点代表一本在Amazon上销售的政治类书籍,节点之间的连边代表两本书被同时购买的可能性高［10］。该网络的节点被分为l、n和c三类,分别代表“自由派”、“保守派”和“中间派”。football数据集是根据美国大学生足球联赛而创建的一个复杂的社会网络。该网络包含115个节点和616条边,每一个节点代表一只球队,节点之间的连边代表球队之间曾经进行过比赛,由于球队属于不同的州,每个州内的比赛场次多,因此该网络被分为12个社区［10］。

对网络社团结构的研究来自于社团学,已经历经了很长时间。社团结构分析与计算机科学中的图分割和社会学中的分级聚类密不可分,并且在大规模的复杂网络中寻找社区或者发现社区的过程中,可以符合客观条件的使用。

2.2 实验结果

GN-PR的总体算法思想是首先对图进行基于GN方法的社区划分,其次使用PageRank算法在每个社区内部进行节点的排序,最后根据社区重要性进行节点的挖掘。为了验证算法的性能,我们使用polbooks和football两个数据集进行实验。

2.2.1 社区划分的结果示意图

图2 为polbooks 数据集的可视化结果,该数据集中包含105 个点和441 条边；图3 为football 数据集的可视化结果,该数据集中包含115 个节点和616 条边。（a）（c）分别为polbooks 网络和football 网络的原始结构示意图,根据GN 算法进行社区划分,可视化结果如（b）（d）所示,其中社区以不同颜色进行区分,在Q 值最大的情况下,polbooks 网络中实验结果显示网络被划分为四个社区,football网络被划分为五个社区。

图2 polbooks数据集

图3 football数据集

2.2.2 节点排序输出

在社区划分的基础上,我们在每个社区内部使用PageRank 算法计算每个节点的PR 值并按从大到小的顺序排序,选出每个社区内PR值最大的节点,接下来统计每个社区内的节点数目,根据节点数目的大小对社区进行排序,在社区排序的基础上,对每个社区内的首位节点进行排序。

表4 和表5 中为分别使用polbooks 数据集和football 数据集实验的结果,根据紧密中心性（Closeness Centrality）、随机选取（random）、PR（PageRank）值和GN-PR 方法对节点进行排序,每列为按照降序排序节选出的节点ID。

表4 polbooks数据集节选出的节点

表5 football数据集节选出的节点

2.2.3 节点重叠影响力

表6 分别为polbooks 和football 数据集在进行独立感染模拟后,感染节点交集数量的平均值。为了测试节点重叠影响力,我们使用IC 模型对节点进行独立感染,对于每个被感染的节点,以0.15的概率感染周围的节点,模拟次数为100。我们将被感染多于1次和2次的节点数量都取了平均值,P1：被感染多于1次的节点数量的平均值；P2：被感染多于2次的节点数量的平均值；虽然每次的测试具有随机性,但本文GN-PR 方法的交集数量取平均后基本都小于其他方法的平均交集数量,因此GN-PR方法在节点的重叠影响力方面进行了一定程度的削弱。

表6 不同算法在不同数据集中的节点重叠影响力

2.2.4 评估节点传播能力

针对实验数据,本文引用节点的传播效率作为影响力最大化的评价指标,使用独立级联模型（IC 模型）在polbooks 数据集和football 数据集中进行验证,测试重要节点的传播程度。为了测试GN-PR算法的性能,我们和传统的算法：随机选取（random）、PR（PageRank）、紧密中心性（Closeness Centrality）进行了比较。本算法传播效率与其他三种算法传播效率对比示意图如图4所示。

图4 不同算法在polbooks数据集（a）和football数据集（b）中实验结果比较

由图4 可以看出,随着感染次数的增加,感染节点的数量也在增加。虽然经过有限的迭代之后所有节点基本都可以被成功感染,但在节点全部被感染之前,相同的迭代次数下,与传统算法相比,本文提出的GN-PR 算法感染的节点数最多。复杂网络中节点的传播模型采用独立级联模型（IC 模型）,可视化节点的传播能力如图4 所示,其中横坐标代表关键节点感染的迭代次数,纵坐标代表关键节点感染的节点数目。可以看出,在相同的迭代次数中,GN-PR 算法效率最高。本文的实验数据在网络上取得了很好的结果,节点的传播效率得到了明显的提高,实验结果表明GN-PR算法传播效率最优。

3 总结与展望

本文研究了复杂网络中重要节点的挖掘问题,它在网络中传播或抑制都起着重要作用。本文首先使用GN算法进行了社区划分,将节点划分为多个集合。通过这种划分,本文可以将整体节点排序转化为局部节点排序。然后,在每个社区内部通过PageRank算法,选出每个社区内PR值最大的节点,通过节点的数量来计算社区的重要性,最后根据社区重要性进行节点的排序输出。虽然基于社区性质的影响力最大化算法在某些网络中可以取得比较好的效果,但是显然这些算法也存在一些缺点,有的网络具备明显的社区结构,有的网络社区结构并不明显,而且还有网络存在社区重叠现象的可能,所以有些网络可能用GN-PR 算法效果并不明显。通过节点数量来评判社区重要性,对于很多数据集并不适用,在进一步的研究中还需要一些更有效的改进。节点的排序输出有很多拓展的可能性,也有很多应用场景,比如最优路径的选择、微博信息推送等。与各种传统的算法实验比较表明,经过本文算法得到的重要节点,在复杂网络中可获得高效率的传播。