某货车司机座椅悬架系统非线性振动分析

甘 达，兰靛靛，2，林鸿森，季佳伟

（1.厦门理工学院 机械与汽车工程学院,福建 厦门 361000；2.福建省客车先进设计制造重点实验室,福建 厦门 361024）

商用车尤其是货车承载能力要求高,其悬架刚度较大,减振性能差,路面激励引起的驾驶室振动问题尤为突出,而且司机驾驶时间长。研究表明［1-2］：如果驾驶员长时间在振动环境中工作,不但会影响驾驶员的身体健康,出现腰疼、背部酸疼等症状,而且极易疲惫,从而引起疲劳驾驶,影响行车安全最终导致交通事故。因此如何有效地隔离和衰减汽车驾驶室内的振动,提高驾驶员的乘坐舒适性,一直是国内外学者研究的重要研究课题。为了衰减来自路面的各种激励,车辆的减振系统主要有3个减振环节,包括轮胎、悬架和座椅,但改变轮胎和悬架的参数对商用车尤其是货车的承载能力和操作稳定性影响较大［3-4］,而座椅是与驾驶员直接接触的部件,设计有优良减振性能的座椅成本低且见效快,因此,货车、大客车往往使用减振性能良好的悬架座椅来减少司机所受的振动,进一步提高乘坐舒适性［5-6］。

研究悬架座椅非线性振动特性的文献往往基于线性化假设,只能近似表达座椅系统具有弱非线性时的动力学。而座椅悬架中包含的弹性元件、阻尼元件、连杆摩擦和碰撞停止等包含了大量的非线性因素［7］,线性化假设带来了较大误差,因此,为了能更全面地反映座椅真实的非线性动力学行为,需要用非线性分析方法更加准确地进行悬架座椅的振动特性研究。

目前对于座椅悬架系统非线性研究的文献较少,但对车辆悬架系统非线性研究的文献比较多,且相对成熟。由于座椅悬架和车辆悬架在构造和工作原理上有较多的相似性,因此,本文用研究车辆悬架非线性的方法应用于座椅悬架的非线性研究上。

陈晓建等［8］在考虑悬架的阻尼力以及弹簧力非线性的情况下,建立了二自由度四分之一车辆动力学模型,采用增量谐波平衡法（IHBM）分析了激励比以及非线性刚度系数对悬架系统动态特性的影响,得到了各次谐波下的幅频特性曲线。赵玉壮等［9］针对整车非线性悬架系统提出了反馈线性化卡尔曼滤波算法,将非线性系统进行了精确反馈线性化。Litak等［10］应用Melnikov函数分析了车辆悬架系统全局同宿轨道非线性参数临界值,考虑车辆悬架非线性,并在此基础上提出了一种对混沌有效的控制方法。上述文献主要采用谐波平衡法、分步线性化法、多尺度法、等效线性化法等研究非线性振动的近似解析方法,有繁琐的中间运算,而座椅悬架系统相较于车辆悬架来说,结构和工作原理更为简单,适用于计算简便的非线性方法。

平均法作为非线性振动的近似解析方法的优势在于不仅能简化计算过程而且能计算幅频和相频特性,能利用平均化方程的特性来分析全局运动性态和受迫振动的稳定性。鉴于此,在汽车悬架的非线性振动研究基础上,将非线性理论应用到某商用车司机座椅悬架的振动特性研究中,建立座椅悬架系统力学模型,采用非线性平均法求解动力学方程得到近似解析解,并得到系统的幅频响应特性曲线,并在Matlab 中应用四阶定步长Runge-Kutta 法求出数值解,所得结果与解析解对比验证,然后分析座椅悬架系统参数变化对座椅共振曲线的影响,最后对座椅垂直方向振动进行稳定性分析,利用李雅普诺夫一次近似稳定性理论得出稳定性条件。

1 系统模型

路面的振动与冲击经过轮胎、悬架、驾驶室地板、座椅传递到车内驾驶员,整个振动传递系统是一个耦合的、非线性和不确定的系统,根据不同的研究对象,须建立不同的力学模型,为了更好地研究座椅悬架系统的非线性振动特性,排除不同路面激励、不同轮胎类型和不同整车悬架参数对座椅振动特性的影响,将人-椅系统从车辆中分离出来,简化为一个非线性单自由度受迫振动模型,如图1所示,路面的振动与冲击经过轮胎和整车悬架传递到驾驶室,地板的振动作为座椅系统的激励输入q,座椅悬架弹簧的弹力为非线性力,如图1所示,假设系统为弱非线性系统,采用三次多项式表示,得出弹簧力的计算公式：

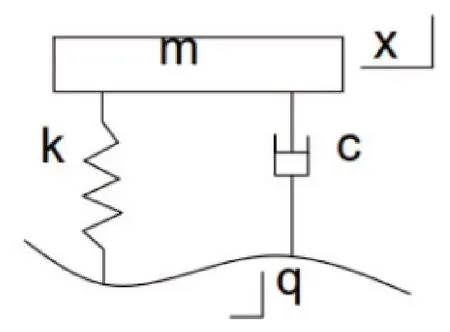
图1 座椅悬架系统模型

F(x)=kx+εkx3（1）

式中,x为弹簧位移；k为非线性弹簧刚度；ε为非线性小参数（0<ε<1）,表示弹簧的非线性程度。

对座椅悬架系统进行受力分析,由牛顿第二定律得到支承座椅悬架系统的振动微分方程表示为：

式中,m 为簧载质量,c1为座椅悬架的阻尼系数,q为车身地板激励。

其中w为激励圆频率,B为激励幅值。

2 平均法求解非线性方程组

由于（4）中的ε是小量,根据平均法的求解步骤,得出（4）的解为：

其中a、θ均为时间t慢变函数。

由（5）可以导出：

将z=acosφ代入

则将式（7）求导再联立式（8）得到：

又有ȧcosφ+aθ̇sinφ=0 则：

同理可得：

此时认定θ和a在φ的一个周期即2π内不发生变化并将上述式子的右项以一个周期内的平均值代替,得出近似的方程组：

积分后得到：

令θ̇=0,ȧ=0 可以得到上述方程组在主共振时的定常解,那么非0平衡点就必须满足方程：

求解上述方程组,消去θ可得主共振时频率w与振幅a之间的关系式：

式（16）是关于a2的一元三次方程,可以绘出不同参数变化的幅频共振曲线。

3 数值仿真分析

为了验证上述平均法的准确性,选择一组参数,进行数值仿真分析。如表1 所示,座椅悬架系统基本参数为：簧载质量m=75 kg,非线性弹簧刚度k=30 kN∕m,阻尼系数c=800 N·s∕m,非线性小参数ε取0.1,底板激励振幅B=0.1 m。

表1 座椅悬架系统基本参数

在Matlab 中进行数值计算,利用四阶定步长龙格-库塔法计算并得到系统幅频曲线。如图2所示,横坐标为频率,纵坐标为相对振幅,在定性方面,解析解和数值解变化的趋势相同即随着频率增大相对振幅增大,到达共振峰以后趋于稳定,在定量方面,共振峰高度分别为0.108 和0.102,相差5.5%,共振频率分别为17.2 Hz和18.6 Hz,相差7.5%,出现误差是由于在平均法计算过程中用平均值来代替某一量进行计算,所以会出现误差,但是在可接受范围（0～10%）内,从而验证了平均法计算过程的准确性,说明本文用非线性平均法研究座椅悬架系统的非线性是有效的。

图2 解析法与数值法所得幅频响应曲线

如图3不同激励幅值对比可知,系统为弱非线性系统,ε取较小值为0.1,非线性弹簧刚度和阻尼系数均不变,在达到共振峰前系统呈现近似线性特性,并且随着激励幅值的增大即B=0.1,0.2,0.4 m时,共振频率分别为17,15,10在逐渐变小,共振峰为0.36,0.38,0.40 在不断增大,增大了5.6%和5.3%,因此由于系统的非线性会导致改变激励幅值对共振频率和共振峰均产生影响。

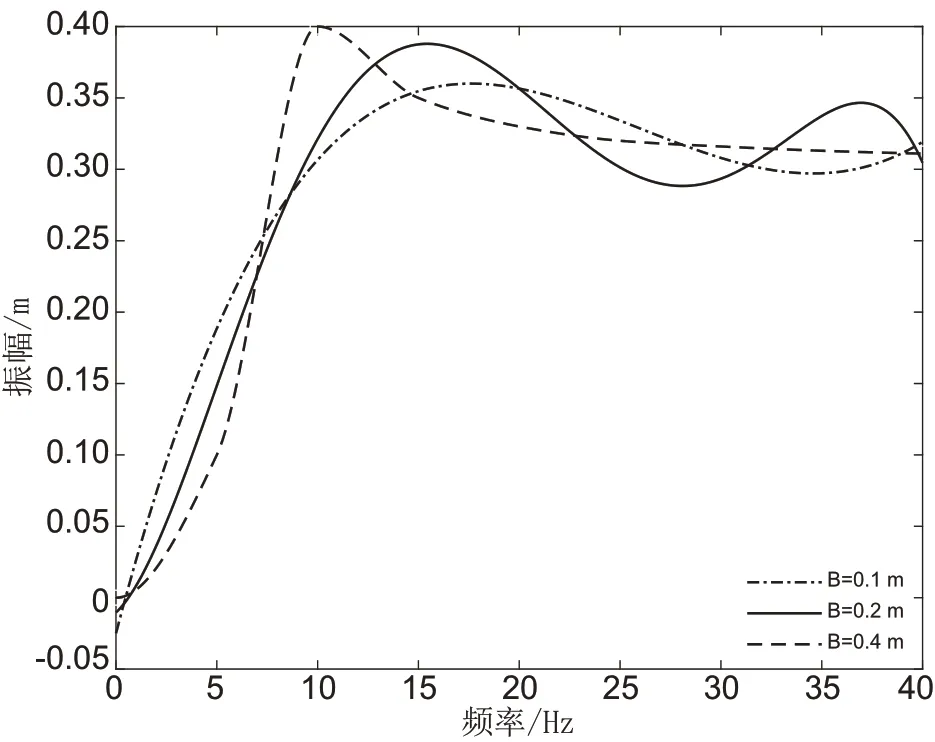
图3 不同激励幅值的幅频响应曲线

考虑ε对乘坐舒适性的影响时,保持其他参数不变,并且保持激励幅值较大（B=1）,改变参数ε的取值,使其分别等于0.3,0.6,0.9,得出幅频曲线如图4 所示,随着ε取值的增大,共振频率不断增大,当ε为0.3 和0.6 时,两条曲线振幅相差小于1%,3 条曲线的共振峰值分别为0.119,0.121,0.122,上升了1.7%和0.8%,且曲线拟合,若只考虑相对振幅,ε取值的大小对乘坐舒适性影响很小。

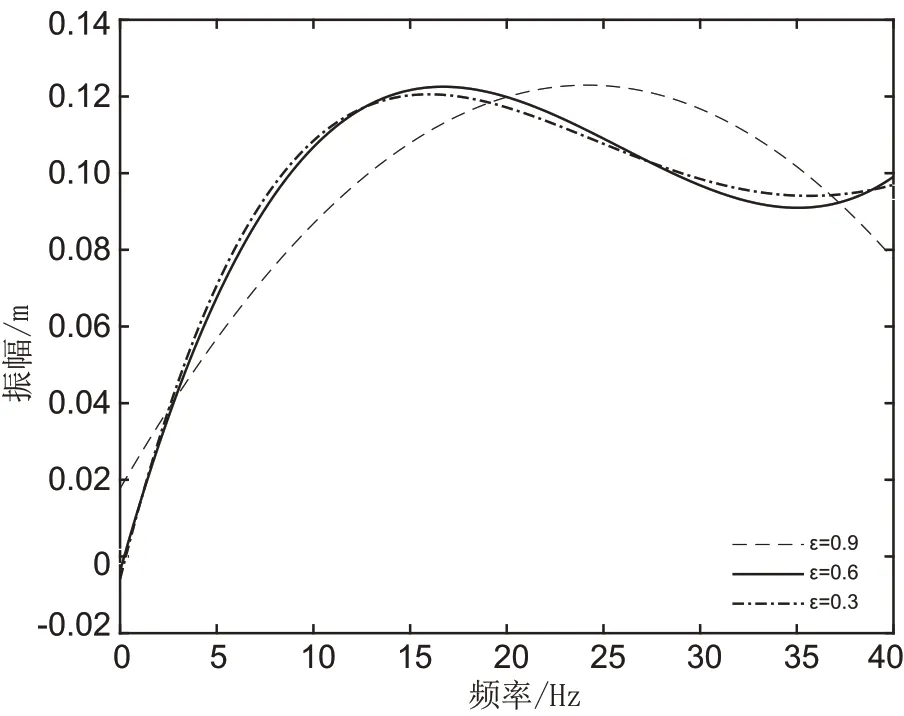
图4 不同ε 的幅频响应曲线

在其他参数不变的情况下,改变非线性弹簧刚度,使其分别为20,40,60 kN∕m时其幅频响应曲线如图5所示,共振峰值分别为0.78,0.82,0.92,上升了5.1%和12.2%,随着非线性弹簧刚度的增加,kε的取值就会增大,非线性程度就越高,座椅相对振幅越大,乘坐舒适性越差。

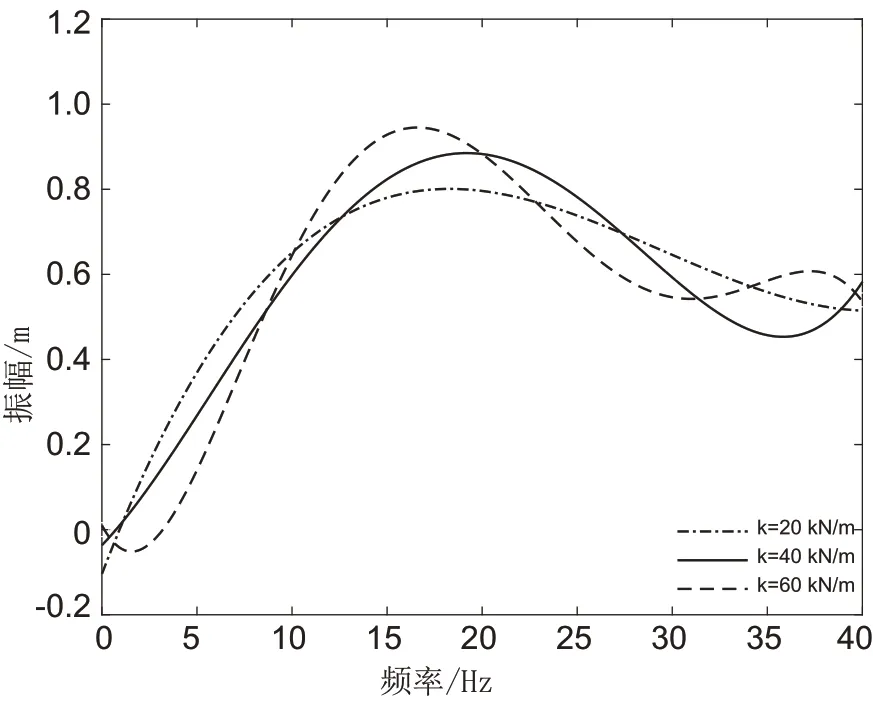
图5 非线性弹簧刚度不同的幅频响应曲线

系统其他参数保持不变,阻尼系数c 分别为800,1 200,1 600 N·s∕m 时对振幅的影响如图6 所示,可以看出,共振频率分别在15,15 和16 Hz,变化很小,因此可以判断得出阻尼对共振频率的影响很小,但是对共振峰值影响很大,共振峰分别为1.1,0.88,0.8,降低了20%和9.1%,阻尼越大,共振峰值越小,并且共振前后,相对振幅变化不大,共振后随着频率的增大,相对振幅趋于稳定。

图6 不同阻尼系数的幅频响应曲线

4 运动稳定性分析

在实际工程问题中常需要判断系统的某种稳态运动是否是稳定的,这需要对系统进行稳定性分析。本文将稳定性问题转化为方程的零解稳定性问题,即解的稳定性由矩阵的特征值决定［11］,其运动的平均化方程为：

引入扰动变量δ=a-a0和η=θ-θ0,列出方程组在奇点(a0，θ0)附近的一次近似式：

其中sinθ0，cosθ0可由上式解出：

线性扰动的特征方程为：

根据李雅普诺夫稳定性理论可知,q<0时奇点(a0,θ0)必不稳定；q>0 时,若P>0 则奇点渐进稳定。在实际情况下,簧载质量、非线性弹簧刚度、阻尼系数等都不可能是负值,对正阻尼情况,c 一定大于0则P>0恒成立,因此得出该系统的稳定性条件为q>0,q<0 为不稳定条件,q=0 则介于不稳定与稳定之间。如图7所示,实线与虚线分别表示稳定区与不稳定区,可以看出频率在3～4 Hz 系统发生了跳跃现象,该跳跃现象的出现可能是由于在非线性系统中,激励频率接近共振频率时,系统发生了共振现象,振幅向下突跃,变得极不稳定,其原因是由于同一频率（3～4 Hz）,会出现多个振幅响应,产生多解的情况,之后随着频率的增大,系统又趋于稳定。

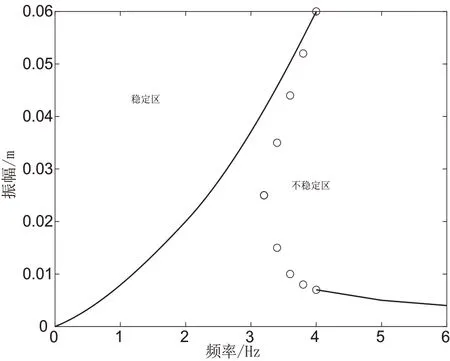
图7 幅频响应曲线上的稳定区与不稳定区

5 结论

针对某货车座椅悬架系统建立了系统模型和非线性运动微分方程,用非线性振动理论的平均法求解非线性运动微分方程并导出了座椅的幅频响应曲线,并用四阶定步长龙格-库塔法进行数值验证,最后进行稳定性分析,得出以下结论：

（1）由平均法求解非线性方程组得出的解析解与数值仿真得出的数值解在定性方面变化趋势相同,在定量方面共振峰分别为0.108和0.102 m,相差5.5 %,共振频率分别为17.2 和18.6 Hz,相差7.5%,在可接受范围（0～10%）内,说明平均法适用于研究座椅悬架系统的非线性振动特性。

（2）采用四阶定步长龙格-库塔法计算并得到系统幅频曲线,对系统进行数值仿真分析非线性参数变化对共振曲线的影响,发现非线性小参数ε的取值在一定范围（0.3～0.9）内取值越大,共振频率越大,共振峰值变化很小仅上升1.7%和0.8%,激励振幅B取值越大乘坐舒适性越差,共振峰值增加了5.6%和5.3%,在一定范围内（k=20～60 kN∕m）,非线性弹簧刚度k 越大,共振峰越大,上升了5.1%和12.2%,非线性特性逐渐增强,因此选择尽可能小的k 值可以提高乘坐舒适性,而增大阻尼系数c的值,共振频率变化小,共振峰值降低了20 %和9.1%,增加乘坐舒适性。

（3）对座椅运动进行稳定性分析,根据李雅普诺夫稳定性理论得出稳定性条件：q>0,并在幅频特性曲线上绘出稳定区域与不稳定区域,可以看出随着激励频率的增加,频率在3～4 Hz 系统发生了非线性跳跃现象,其原因是在这个区间系统发生了共振,所得结果可为座椅悬架系统的优化设计和控制提供理论依据。