需求不确定下基于鲁棒优化的新旧充电站规划

高治佳， 李星梅， 许传博， 王玉玮

(1.华北电力大学 经济与管理学院，北京 102206；2.新能源电力与低碳发展研究北京市重点实验室(华北电力大学)，北京 102206；3.华北电力大学 经济与管理学院，保定 071003)

0 引 言

作为内燃机车辆的理想替代品,电动汽车以其低污染、低排放以及高能源利用率等优势赢得广泛关注[1],大规模的电动汽车入网运行将成为势不可挡的局面[2]。据公安部统计,截至2021年底,我国电动汽车保有量已经达到640万辆[3]。然而,电动汽车行业仍处于发展阶段。其中一个重要原因是充电桩等配套基础设施建设存在缺口[4],现有充电站容量难以满足用户日益增长的充电需求。另一方面,由于用户需求变动或前期规划不合理,已经建成的部分充电站呈现出使用效率低甚至闲置的状况[5],形成了当前电动汽车充电难和充电设施闲置并存的现象。

为了进一步优化电动汽车充电站网络布局,国家发改委和国家能源局联合发布的实施意见中明确指出,充电站运营企业在建设新充电站的同时,可以通过改建、扩容、迁移等方式对已有充电站进行调整[6]。因此,新一轮的电动汽车充电站规划,不仅包括新充电站的选址定容,同时也要对已有充电站的位置和容量做出调整,这一问题也被称作新旧充电站规划问题。

此外,用户充电需求是影响电动汽车充电站选址的重要因素。在实际问题中,用户需求受到众多因素的影响,如电池技术的发展、交通路网状况[7]、用户出行习惯[8]、用户心理因素、电动汽车保有量等[9],具有很强的不确定性。如果在新旧充电站规划过程中不考虑用户充电需求的不确定性,就很有可能出现充电站容量冗余或者服务能力不足的情况。因此,研究需求不确定下新旧充电站规划问题具有现实意义。

需求不确定的常用刻画方式有以下几种:敏感性分析、机会约束模型、随机规划和鲁棒优化。其中,敏感性分析忽略了参数不确定性的影响,主要用来分析模型的参数变化对最优解连续性的影响[10]。另外,机会约束模型和随机规划都需要事先掌握不确定参数的概率或者分布情况[11]。然而,在实际问题中,因为没有足够的可用信息,依靠统计数据并不能准确获得随机参数的概率分布[12]。而鲁棒优化是利用随机变量的统计信息构建不确定集合,不需要提前掌握不确定参数的概率分布[13],即可得到系统最坏情况下的优化方案。因此,本文选择鲁棒优化方法来刻画新旧充电站规划问题中的需求不确定性。

目前,运用鲁棒优化方法解决充电站选址问题中的需求不确定性已经成为国内外学者研究的热点。如Li C等人[14]考虑了电动汽车充电需求和分布式可再生能源输出的不确定性,基于路网和电网结合,提出了一种分布式能源充电站选址的鲁棒优化模型。赵峰等人[15]针对高速公路并网光储充电站选址定容中需求不确定性问题,提出了一种基于数据驱动的分布式鲁棒优化的两阶段选址定容方法。Hao S等人[16]研究了不确定条件下的多区间换电站选址以及充电规划问题,采用鲁棒优化的方法来处理问题中的需求不确定和电价不确定。Khardenavis A等人[17]通过考虑动态充电需求、投资成本、接入距离、电网连接时间等因素,提出了一种城市充电基础设施规划鲁棒模型。从目前已有的文献来看,基于不确定集合的充电站选址研究成果较多,但还没有人考虑需求不确定下基于鲁棒优化的新旧充电站规划问题。因此,本文采用鲁棒优化的方法对需求不确定下的新旧充电站规划问题进行建模,使选址结果即使在最坏情况下,也能够满足用户充电需求。

综上所述,本文的主要贡献在于:(1)针对新旧充电站规划问题,本文充分考虑了在实际问题中用户充电需求的不确定性。(2)采用鲁棒优化方法,引入不确定情境集来刻画用户需求的不确定性,并通过不确定预算来调节不确定集合的大小,满足决策者的不同风险偏好程度。(3)最后,以上海市杨浦区电动汽车充电站选址问题为例,验证了本文所建模型和求解方法的可行性和鲁棒性。

1 问题与模型

为了研究新旧充电站规划问题,假设区域内已经存在m个不同等级的充电站,决策者正在考虑是否需要调整这些旧充电站。与此同时,有n个候选点用于建设新充电站,决策者需要确定新充电站的数量、位置和等级。由于文章涉及符号众多,为了便于后续模型的构建,在附录1中给出了模型中涉及的集合、参数和变量的含义。

1.1 新旧充电站规划模型构建

当需求点i处的需要充电的电动汽车的数量wi已知时,新旧充电站规划模型DM如下:

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

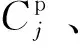
1.2 新旧充电站规划鲁棒模型

1.2.1 不确定情境集构建

这一小节将考虑用户充电需求不确定下的不确定情境集的构建。由于在实际问题中,决策者很难准确的获得用户需求的概率分布信息,因此,我们引入了如下不确定集合。

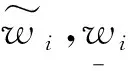
(13)

进一步地,我们引入“不确定预算”的概念,令Γj(j=1,2,…,m,m+1,…,m+n)表示不确定预算,那么包含不确定参数的约束里所有的不确定参数的相对偏离度之和不能超过Γj,用数学公式可以表述为

决策者可以通过改变不确定预算的值来调节不确定情境集的大小,从而客观衡量约束条件的保守程度。在本文中,Γj的值越大,不确定情境集的范围就越大,决策者的风险追求偏好程度也就越高。

1.2.2 新旧充电站规划鲁棒模型构建

在新旧充电站规划问题中,最坏情况下选择到规划点j充电的电动汽车数量也不得超过该点充电站的服务能力,用数学语言可以表述为

(15)

(16)

(17)

(18)

上述模型中公式(16)是非线性的,为了方便计算,我们根据对偶理论,引入对偶变量vi和vj,将内层最大化问题转化为最小化问题,得到公式(19)～(22):

(19)

(20)

vi≥0,i=1,2,…,|I|,

(21)

(22)

综上所述,需求不确定下基于鲁棒优化的新旧充电站规划外层模型RM可以写成如下形式:

(23)

该模型为混合整数规划线性模型,包含(|I|+|S|+5)(m+n)个二进制变量,(14+|S|)(m+n)+2|I|+1个连续变量,(4|I|+2|S|+7)(m+n)+5|I|+1个约束条件,运用MATLAB R2017a平台对混合整数规划模型进行编程,并使用YALMIP工具箱调用GUROBI 8.0.1求解器在Intel(R) Core(TM)i5-1135G7@ 2.40GHz 2.42 GHZ环境下进行求解,计算时间在1.679 729～ 2.984 922 s之间。

2 算例分析

2.1 算例描述

上海市作为新能源汽车推广的示范城市之一,近年来电动汽车市场发展迅速。为了验证本文所构建的模型的合理性和有效性,本节算例选取了上海市杨浦区作为研究对象。需求点和充电站规划点数据均来自参考文献[18]。根据北京市出台的标准文件《电动汽车电能供给与保障技术规范: 充电站》,在该算例中,规定充电站的建设分为 4 个等级,每个等级的充电站的建设成本和服务能力参考文献[19]。每升一级的改造成本为50.13万元,各等级充电站的运营成本和拆除收益分别为建设成本的10%和5%[19],充电站的服务半径为3 km,运行年限为 20 年,贴现率为8%,充电单价为 1.2 元/kW·h,电动汽车单次充电电量为40 kW·h[18],单台充电桩功率为96 kW[20],初始预算为1 000万元,这些参数的设置都在合理的范围内。另外,在本节考虑不确定预算Γj取值为1的情况。

2.2 场景设计

为了进一步凸显本文所建立的模型的优势和模型的求解结果,在本节设计了两种模型场景进行分析和比较。

场景1:在电动汽车用户充电需求确定条件下,对已有充电站规模进行调整,并且确定新充电站的数量、位置和等级,即上一节所建立的新旧充电站规划模型DM。

场景2:在电动汽车用户充电需求不确定条件下,对已有充电站规模进行调整,并且确定新充电站的数量、位置和等级,即上一节所建立的新旧充电站规划鲁棒模型RM。

2.3 求解结果

本小节根据上述数据分别对模型DM和模型RM进行求解,并对求解结果进行对比分析。

表1给出了场景1和场景2最终的求解结果,图1展示了规划前后两种场景的选址数量、位置和等级。

图1 选址结果对比Fig.1 Comparison of site selection results

表1 模型求解结果

观察表1和图1,我们发现,场景1的最终选址方案中,在15个规划点中只选择了5个建设充电站,同时,建设等级也均为1等级或者2等级的充电站。从成本的角度来看,该方案的投资总成本相对较低。与场景1相比,场景2的选址方案中最终选择的充电站数量较多,高等级的充电站数量也更多,与此同时,各类经济成本也有不同程度的增加。原因在于,在场景2中考虑了用户需求的不确定性,建设了更多的充电站以满足最恶劣情况下的用户需求,直接导致了规划成本和运营成本的增加。

此外,由于电动汽车用户充电需求不断上升,为了比较两种场景应对未来需求增加风险的能力,我们将各个需求点的现有需求量增加20%作为预期需求量,图2展示了需求增加20%时场景1和场景2充电站容量对比情况。不难看出,在场景1中,现有充电站规模几乎刚好可以满足当前用户充电需求。观察图2,当用户充电需求增加20%时,5个充电站点的日服务能力都无法满足用户需求,这将大大降低电动汽车用户充电体验。对比场景2,在考虑了需求不确定性的鲁棒选址模型的建站结果中,现有充电站规模不仅能很好的满足现有用户充电需求,即使用户充电需求增加20%时,目前的规划结果仍能够满足预期用户需求量,且与充电站的最大日服务容量相比,仍有缓冲空间。

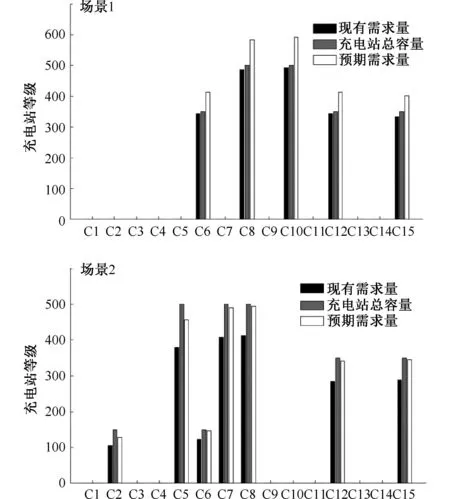
图2 需求增加20%时容量对比Fig.2 Capacity comparison when demand increases by 20%

综上所述,经过对比可以得到以下三点结论:

(1)需求已知的确定型选址模型在规划成本、网损成本和运营成本上都具有较大优势,但由此产生的问题是,它处理用户需求不确定性的能力较弱,当用户充电需求增加时,现有选址方案的充电站服务能力远远不能满足用户充电需求。

(2)考虑需求不确定下的鲁棒选址模型虽然会增加初始投资成本,但可以很好的应对未来用户充电需求增加的情况。

(3)从风险响应和用户充电需求增加的趋势来看,相比于需求已知的确定性选址模型,本文构建的考虑用户充电需求不确定性的鲁棒选址模型更符合实际,更有利于用户充电需求的满足。

2.4 敏感性分析

本文所构建的考虑用户充电需求不确定性的新旧充电站规划鲁棒选址模型是通过改变不确定情境集的大小来实现的,当参数在给定的集合内发生变化时,都能确保优化方案可行。在正常情况下,模型解的最优性会随着其鲁棒性的增加而降低,因此,本节将对不确定预算Γj进行敏感性分析,进一步探讨模型鲁棒性和最优性之间的关系。

图3给出了各类经济成本随着不确定预算的变化趋势图,图4以热力图的形式给出了不同不确定预算下的选址结果。

图3 不同不确定预算下成本变化趋势Fig.3 Cost trends under different uncertain budgets

图4 不同不确定预算下选址结果Fig.4 Site selection results under different uncertain budgets

观察图3,随着不确定预算Γj在0到1之间增加时,规划成本、网损成本和运营成本均呈现出增加的趋势,特别地,规划成本和运营成本的变化幅度较大,这也直接导致了总成本的大幅度增加。结合图4可以发现,随着不确定预算Γj的增加,各等级充电站比例变化不大,但充电站总数量由最开始的4个变成了7个。这是因为随着不确定预算的增加,可行解空间变大,这意味着每个需求点的用户充电需求都在增加,为了满足最恶劣条件下的充电需求,需要建设更多的充电站,用来提高充电效率和用户满意度。

根据上述分析,可以得到以下两点结论:

(1)模型鲁棒性的提高主要表现在充电站数量的增加上。不确定预算越大,模型的鲁棒性越强,所建充电站的数量越多,相应地,需要的投资成本也越高。

(2)不确定预算在一定程度上可以衡量决策者的风险偏好。如果决策者为风险追求偏好,则可选取较小的不确定预算,但此时就要承担充电站服务能力不能满足用户充电需求的风险;如果决策者为风险规避偏好,则选取较大的不确定预算,为选址方案的有效可行提供较大的概率保证,但需要以付出更多的投资成本为代价。

3 结 论

(1)相较于需求确定的充电站选址模型,本文所构建的需求不确定条件下新旧充电站规划的鲁棒模型更符合实际,可以更好地应对未来用户充电需求增加的情况,即使未来用户充电需求增加20%,目前的规划结果仍能够满足预期用户需求量,且与充电站的最大日服务容量相比,仍有缓冲空间。

(2)在新旧充电站规划鲁棒模型中,鲁棒性的提高主要通过增加充电站的数量来实现。不确定预算越大,模型的鲁棒性越强,所建充电站数量越多,相应地,需要的投资成本也越高。

(3)不确定预算对投资成本和建站数量有显著影响,决策者可以根据自己的风险偏好程度来选择不同的选址方案,本研究为上海市杨浦区电动汽车充电站选址问题提供了参考。

附录1

文章中涉及的集合、参数和变量的含义。

集合

I：电动汽车用户需求点集合，i∈I，i=1，2，…，|I|；

J：电动汽车充电站规划点集合，包括m个已有充电站规划点和n个新充电站候选点，j∈J，j=1，2，…，m，m+1，…，m+n；

汞的毒性很大，对人类健康造成极大危害。日本、加拿大、挪威、伊拉克和美国等国都曾发生过汞中毒事件，例如在1953—1960年期间，日本水俣市发生了汞中毒而引起的疾病——水俣病，从而引起了世人的关注[19]。

S：规划后充电站等级集合，s∈S，s=1，2，…，|S|；

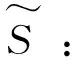
参数

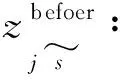
dij：需求点i与规划点j之间的距离；

wi：需求点i处的需要充电的电动汽车的数量；

pi：需求点i处的电动汽车正常运行时的功率；

Qs：等级为s的充电站日服务能力；

c：每台充电桩线路损耗和充电损耗；

l：每台充电桩的额定功率；

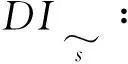
Cup：已有充电站的升级产生的成本；

Cdown：已有充电站降级获得的回收资金；

Cs：等级为s的充电站的建设成本；

qs：等级为s的充电站的运营成本；

p：单位售电成本；

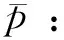
W：总建设投资预算；

R：用户所能接受的最远充电距离；

T：充电站每天有效工作时间；

r：贴现率；

t：充电站的使用寿命；

变量

yj：0-1变量，规划后点j有充电站时取值为1，否则为0；

zjs：0-1变量，规划后在点j建设等级为s的充电站时取值为1，否则为0；

xij：0-1变量，需求点i的用户选择到规划点j进行充电时取值为1，否则为0。