大型风机海上风电场集电系统拓扑优化

吴 瑊， 米增强， 杨玉新， 栾福明， 李 程， 刘玉成

(1.新能源电力系统国家重点实验室(华北电力大学)，北京 102206；2.中国大唐集团科学技术研究总院有限公司 华北电力试验研究院，北京 100040；3.大唐汕头新能源有限公司，广东 汕头 515910)

0 引 言

海上风电具有大规模开发可行性高、资源丰富、发电利用小时数较大等优点[1],我国海上风电发展以潮间带和近海为主,未来海上风电将呈现规模化、集群化、深远海化的发展趋势,预计年新增装机容量将在2025年超过20 GW,并有望在2030年达到40 GW[2,3]。与陆上风电投资以风电机组成本为主不同,其风电机组间距更大,海底电缆成本昂贵,集电系统投资占整个海上风电场成本最高可达近30%[4]。为降低海上风电投资成本,集电系统拓扑优化成为重要的技术方向之一[4]。由于风电机组额定容量存在增大的趋势[5],集电线路电压等级随之向更高电压等级发展[6],使用不同电压等级的集电系统,串组风电机组数量跨度大且串组密度差异性大,以规划容量1 000 MW、单机容量为7 MW的风电机组风场为例,采用35 kV集电系统的串组数量为采用66 kV集电系统的近一倍,且单回路连接风机数量只有66 kV集电系统的1/2左右[7],当单机容量发生变化时,集电系统的串组数量及单回路连接风机个数将会产生较大差异,进而对集电系统拓扑布置结构产生较大影响,在保证计算效率的前提下,提高优化算法的普适性及经济性为重点研究方向之一。

海上风电集电系统拓扑优化不同于陆上需考虑地形高度对于拓扑结构的影响,是二维空间中以经济性为优化目标的路径寻优问题,这表明,拓扑结构的空间分布为优化过程核心,文献[8]采用遗传算法进行海上风电场集电系统拓扑优化,将动态边权最小生成树算法(DMST)引入遗传算法初始种群产生过程,并改进算法编码方式,提升了拓扑优化的寻优性及收敛性,但未考虑采用不同电压等级集电系统拓扑结构布局的变化对编码方式及编码效率的影响。文献[9]通过改进蚁群算法的择路策略[10]及信息素更新策略,提高了拓扑优化的寻优性及有效性,但未考虑不同电压等级集电系统下,采用不同单机容量风电机组时单回路风机数量差异性对择路及信息素更新策略的影响。上述算法可通过设置惩罚函数、调整参数等方式,实现寻优求解,由于算法策略不能整体在集电系统电压等级及单风机容量改变对拓扑结构空间分布的影响,可能陷入局部最优。

FCM算法以空间位置及空间分布为聚类基础,将原有结构调整为以升压站为聚类中心的放射状聚类,以空间结构为角度进行降维经济性寻优计算,减少寻优结果陷入局部最优的可能性。使用基于海缆串组载流量的趋近边权算法,以降低随机计算对于算法效率的影响,使优化结果更快速地根据拓扑优化边权条件收敛。且将路径寻优、经济性寻优、海缆路径不交叉、海缆串组载流量不得过载等多任务的复杂边权条件分解降维为独立的计算问题,进一步的提高了算法的整体计算效率及得到最优经济解的概率。在分解降维后,多采用Prim算法[8]、Kruskal算法等,将集电系统拓扑经济性寻优问题转化为图论问题,应用对象为全体节点及连线,整体效率较低,需进行改进优化,提高计算效率。

文献[11]基于FCM算法,在考虑损耗约束的前提下,对海上风电集电系统设计方式进行了充分的论证,但未考虑FCM算法在集电系统电压等级后进行拓扑结构优化的普适性及经济性变化。本文根据集电系统拓扑优化的边权条件,改进FCM算法聚类结构及优化路径选取算法,通过判断串组空间位置关系、风电机组坐标点位置关系等限制条件,解决不同电压等级的集电系统串组风电机组数量跨度大且串组密度差异性大的问题,以某海上风电场算例为基础,验证本文方法的寻优性、普适性及规划效率。

1 集电系统拓扑优化模型

海上风电场集电系统汇集风电机组电能并输送至海上升压站,在规划集电系统拓扑时,多采用放射形结构[12],可将风电机组视为顶点、海上升压站视为根节点,海缆抽象为各点间的连线。以升压站(根节点)为中心进行模型抽象,使用图论的思想解决上述问题[13],各顶点赋值为风电机组额定容量,分段海缆成本作为边权。

海上风电场集电系统优化的约束条件复杂,如各段海缆布线不可交叉、海缆上连接风电机组的数量受海缆载流量的限制等。在模型设计阶段,使用改进FCM算法将整体集电线路规划进行降维,分区域、分串组处理,利用分区优化的方式可避免各串组海缆布线出现重叠,符合约束条件限制。在拓经济性寻优方面,改进Prim算法优化串组路径,以切分定理为基础,按照设定的边权条件生成严格的最小生成树,保证优化结果在边权条件限制下的最优性。在海缆选型方面,不同型号的海缆有不同的载流量、电阻、横截面积及价格。本文选用海缆的环境条件为:海底或滩涂段直埋;环境温度25 ℃;深埋1 500 mm;土壤热阻系数1.2 K·m/W。本文选用国内某厂商生产的不同电压等级海缆,其具体参数(单位造价不含敷设施工)如表1所示。

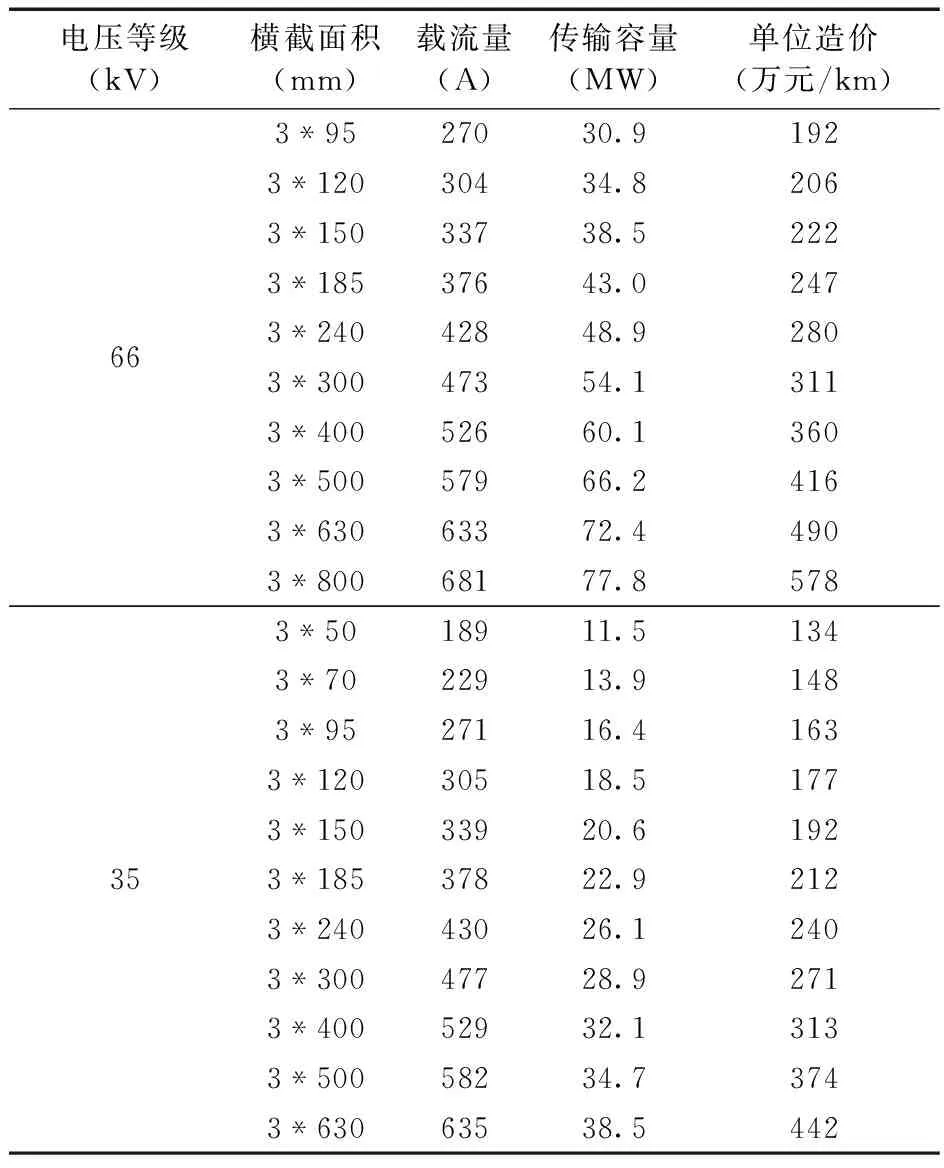
表1 海缆参数

1.1 目标函数

集电系统拓扑优化目标是寻求相对经济性最优,主要投资成本(不包含敷设施工)包括风电机组变压器、风电机组环网柜、集电海缆、升压站等部分,本文选用国内某厂商生产的两种电压等级电气设备,其具体参数如表2所示。

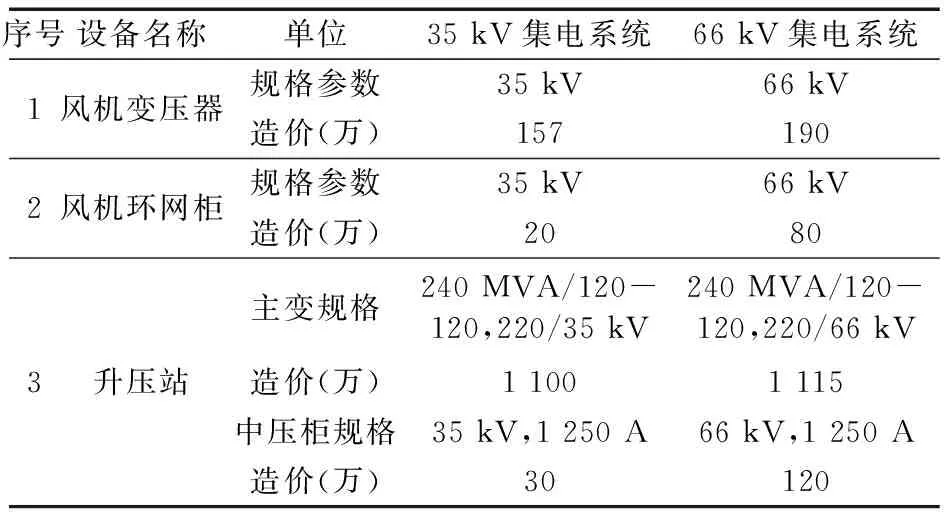
表2 海上风电场集电系统主要投资成本

风电机组变压器及风电机组环网柜数量将等于风电机组数量,此部分购置成本为

Ct&s=Nwt×(Ptrans+Pswitchgear)

(1)

式中:Ct&s为风电机组变压器及风电机组环网柜总价;Nwt为风电机组数量;Ptrans为风电机组变压器单价;Pswitchgear为风电机组环网柜总价。

大型海上风电场通常选取多种不同型号的海缆,在计算第i节海缆的传输容量后,将通过匹配表1得出海缆单位长度价格Pi,此部分购置成本为

(2)

式中:Ccable为海缆总造价;Ncable为集电系统海缆分段数量;(xi1,yi1)、(xi2,yi2)分别为第i段海缆两端的风电机组坐标。

升压站的购置成本可根据海上风电场实际需求而定,此部分购置成本为

Csubstation=Ns×Psubstation

(3)

式中:Csubstation为升压站总价;Ns为升压站数量;Psubstation为升压站单价。

海上风电场集电系统的主要投资成本为

Ctotal=Ct&s+Ccable+Csubstation

(4)

式中:Ctotal为集电系统的主要投资成本。

1.2 约束条件

集电系统拓扑优化的约束条件分为海缆载流量约束及布线不可交叉。受串组海缆载流量限制,连接的风电机组总容量不可高于所选海缆载流量最大的分段,此约束条件可表示为

(5)

式中:Nt为串组i内挂载风电机组的总数;Cij为串组i内第j个风电机组的容量;MAX(Ci)为串组i连接升压站海缆分段的最大视在功率。

受式(5)限制,需计算串组风电机组最多数量,在风电机组型号相同前提下,串组i的Cij可表示为

(6)

式中:Pt为单个风电机组的额定出力;Uc为所选海缆的额定电压;cosδ为功率因数。

串组i中海缆分段的最大载流量应不低于Cij总和,结合式(5)及式(6)并代入最大载流量,为串组i最多风电机组数量,可表示为

(7)

其中,Imax为横截面积最大的海缆的最大载流量。

考虑海缆的安装及实际工程需求,本文将通过改进FCM算法将集电系统分区,避免串组海缆间出现交叉,本算法的隶属度函数为

(8)

式中:uij为风电机组j对于聚类中心i的隶属度;c为聚类中心个数,即串组数量;dij=‖ci-xj‖为第i个聚类中心与第j个风电机组间的欧氏距离;dkj=‖ck-xj‖为聚类中心与第j个风电机组间的欧氏距离;m为隶属度加权因子,m∈[1,∞)。

如图1所示,上述算法的聚类分区未考虑升压站与串组间的位置关系,不能避免串组交叉。为使分区呈放射状,风电机组聚类分区的方法如图2所示,升压站设为坐标点o,dij为风电机组j到升压站o与聚类中心ci连线的距离,计算矢量oj与矢量oci间的夹角θ。如果θ大于90°,则dij=j;反之,dij=dij*sinθ。

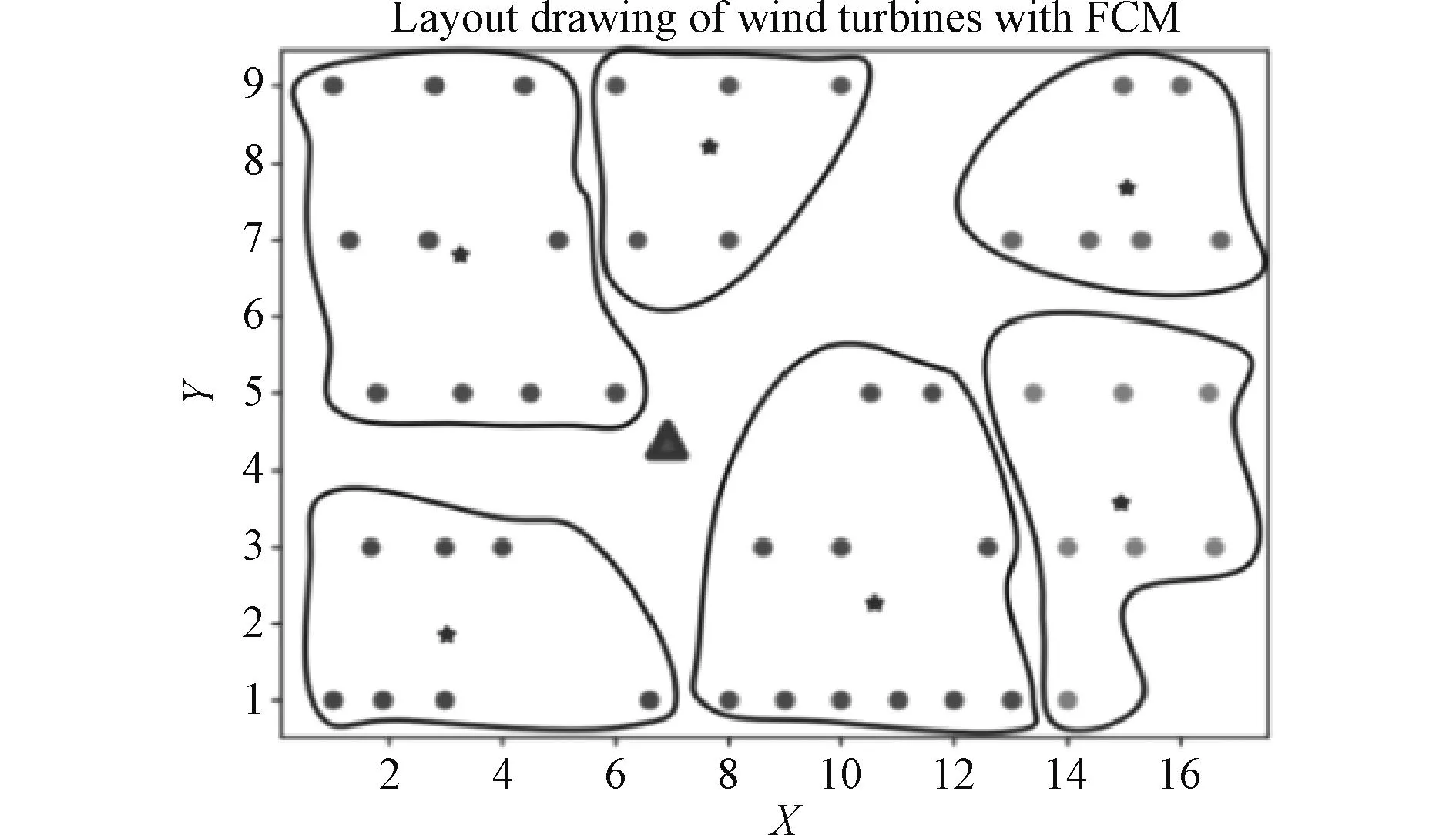
图1 FCM算法聚类结果图Fig.1 Graph of original FCM algorithm clustering result

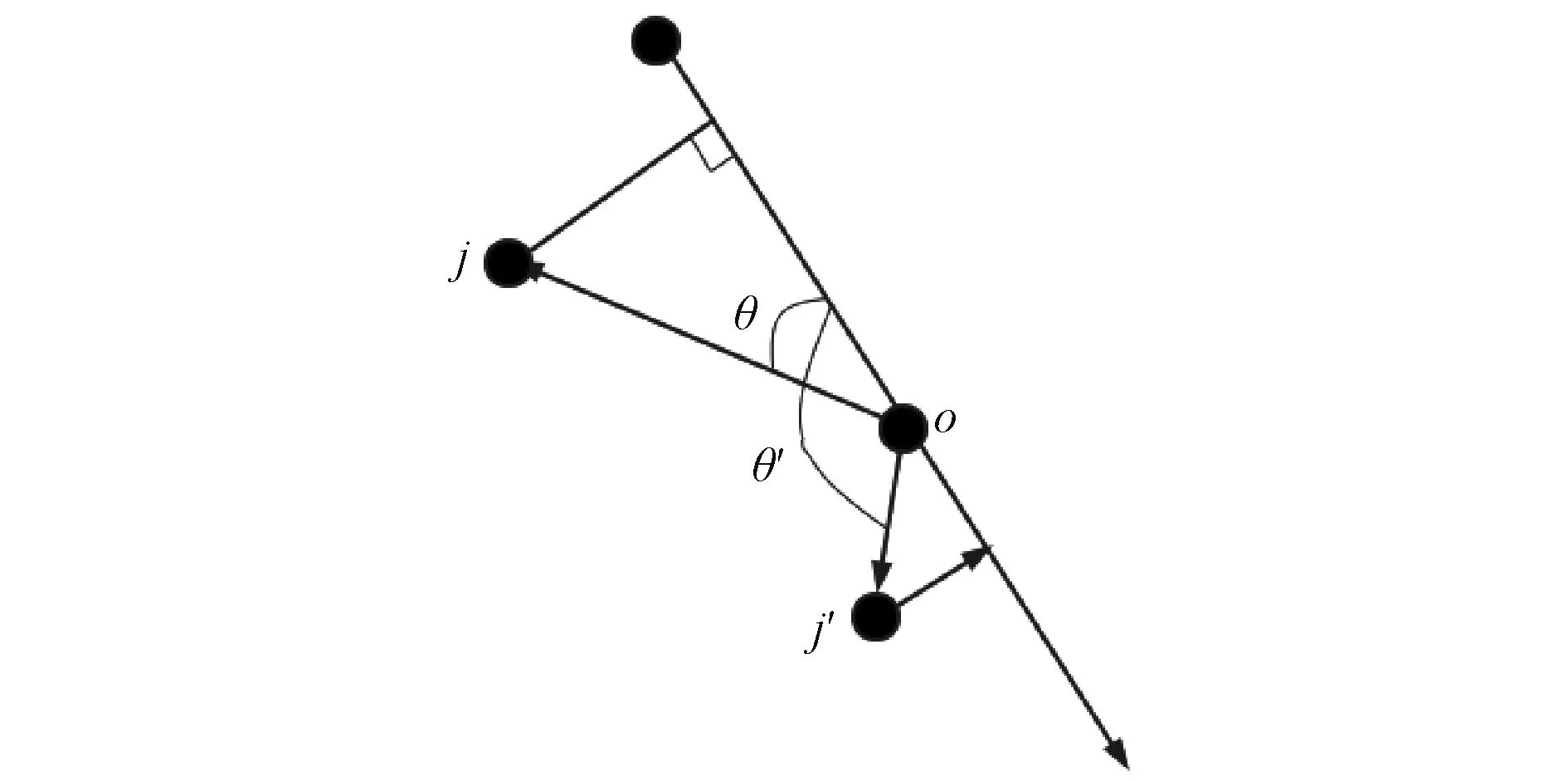
图2 风电机组到类心的距离示意图Fig.2 Schematic diagram of the distance from the wind turbine to the cluster center

基于图2方法的FCM算法[11]可满足述约束条件,但其迭代的聚类结果无递进性,计算效率较低,本文提出一种改进FCM算法的新迭代架构及避免海缆交叉的判定方式。

2 改进FCM算法设计

FCM算法采用轮盘赌算法获取聚类中心(类心),判断区域内风电机组数量是否满足串组挂载风电机组总容量不高于海缆最大载流量的限制。符合限定条件后,使用聚类分区结果进行区域内成本最优拓扑规划;反之,使用轮盘赌算法获取类心后进行迭代。当迭代次数超过设定值时,增加类数量(串组数量)。FCM算法迭代的类心通过多次随机聚类、增加串组数量的方式获得向限制条件收敛的聚类分区结果,此结构不能依据边权条件有效向限制条件收敛,严重影响算法的计算效率及分区的寻优性。

为提高算法的整体计算效率及寻优性,本文将从FCM算法的内外循环结构、补充隶属度算法、串组位置关系判断等方面提出解决方案,并基于Prim算法,以经济性为寻优目标,进行最优路径选取,实现海上风电场集电系统拓扑经济性优化。

2.1 FCM算法结构改进

改进FCM算法的内循环结构可获取区域划分结果,如图3所示,设定迭代差值(eps)后,采用轮盘赌算法获得初始类心,计算迭代结果的隶属度矩阵的总和(迭代和)及迭代和间的差值,进行判定:1)风机数量是否满足区域(串组)风电机组总容量不高于海缆最大载流量;2)迭代和差值是否大于eps。满足判定条件之一,进入外循环结构。内循环结构设置判断条件2的原因为:两次迭代和间的差值小于eps,表明迭代的聚类分区结果相似且不满足条件1,不能有效地向限制条件收敛。

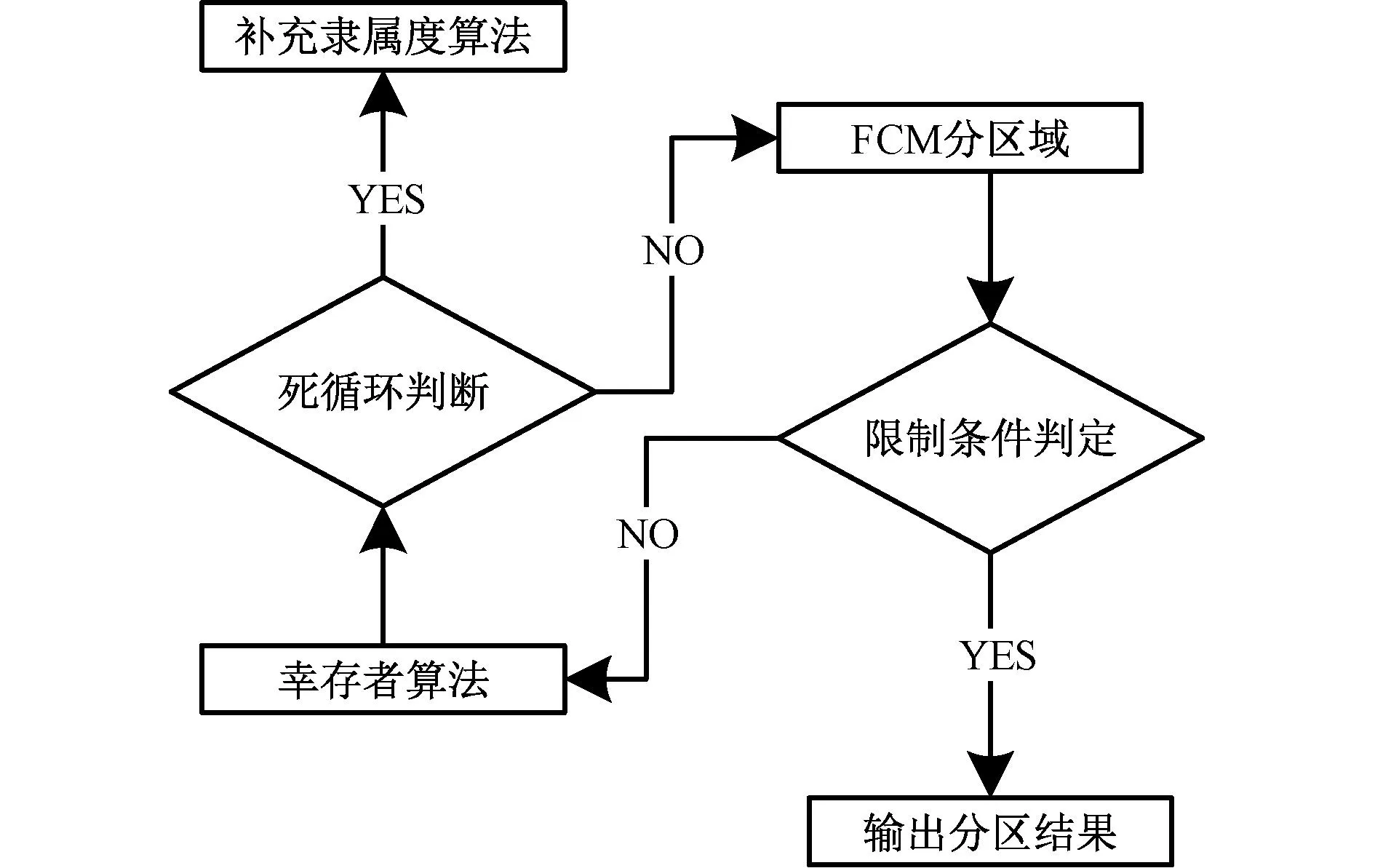
图3 改进FCM算法内循环流程图Fig.3 Flow chart of improved FCM algorithm inner loop

若分区结果不满足条件1,使用幸存者算法,获取隶属度矩阵,对区域内各风电机组的隶属度值降序排列,依据条件1,保留隶属度值高的风电机组。未选取的风电机组进行二次分区,使用风电机组对各分区的隶属度值,将其分配到隶属度值次高的区域,降低FCM算法分区的随机性,使分区结果在保证寻优性的基础上主动向限定条件收敛。

隶属度值次高的区域唯一时,则完成分区;反之,风电机组将循环随机分配于多个区域,不能收敛,使用补充隶属度算法,即加权K-means算法,加权可保持隶属度值量级不变,其隶属度可表示为

uij=λ‖ci-xj‖

(9)

式中:uij为风电机组j对于聚类中心i的隶属度;xj为风电机组j的坐标;ci为聚类中心i的坐标;λ为权值。

改进FCM算法的外循环结构如图4所示,使用内循环条件2,分区可能不满足限制条件,外循环设置判定条件如下:1)各串组内风机坐标连线分别形成的凸多边形是否重叠;2)风机数量是否满足区域(串组)内风电机组总容量不超过海缆最大载流量。若满足两个判定条件,进行区域内成本最优拓扑规划;反之,增加迭代次数并判定迭代次数是否超过限值。未超限值,则返回内循环进行迭代聚类;反之,增加类心个数后进行区域划分。通过外循环迭代可以减小因随机性引起的串组数量改变,保证算法的寻优性。

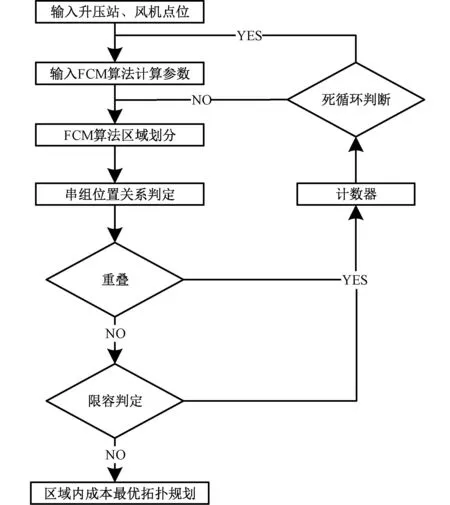
图4 改进FCM算法外循环流程图Fig.4 Flow charts of improved FCM algorithm outer loop

2.2 串组位置关系判断

如图5所示,首先判定串组内各顶点(包括升压站坐标)是否共线,若串组顶点(包括升压站坐标)均共线无法构建凸多边形,不能直接判断串组凸多边形间重叠面积,使用虚拟面积法,选取串组内坐标中心,在不影响串组空间位置的前提下,围绕其添加四个顶点,构建虚拟凸多边形。

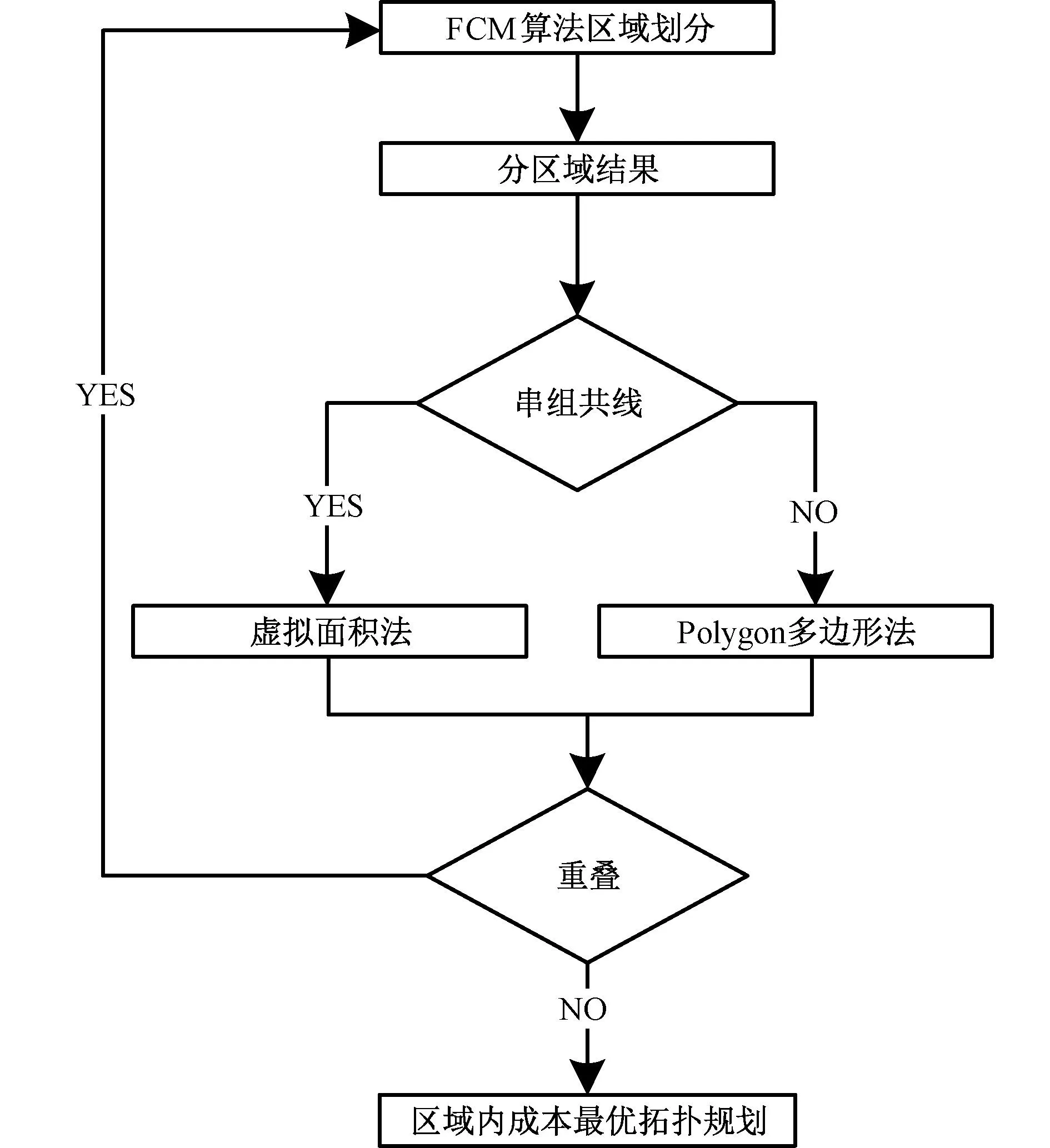
图5 串组位置关系判断流程图Fig.5 Flowchart for judging the positional relationship between strings

若不存在共线情况,使用Polygon[14]构建凸多边形。各凸多边形依次判定是否重叠,如图6所示,存在重叠面积时,区域内海缆存在交叉布线的可能性,需重新分区。串组位置判定与判定线段交叉[15]不同,判定线段交叉以分段海缆为判断对象,需遍历每段海缆,逐一进行位置关系判定。串组位置判定以串组为判断对象,结合模式识别理论,有效提高计算效率。

图6 凸多边形面积比较图Fig.6 Comparison figure of convex polygon area

2.3 Prim算法路径选取优化

Prim算法[16]路径选取优化的流程如图7所示,其边权条件为本文1.2节的目标函数,为提升计算效率,引入Delaunay三角剖分法[17]。

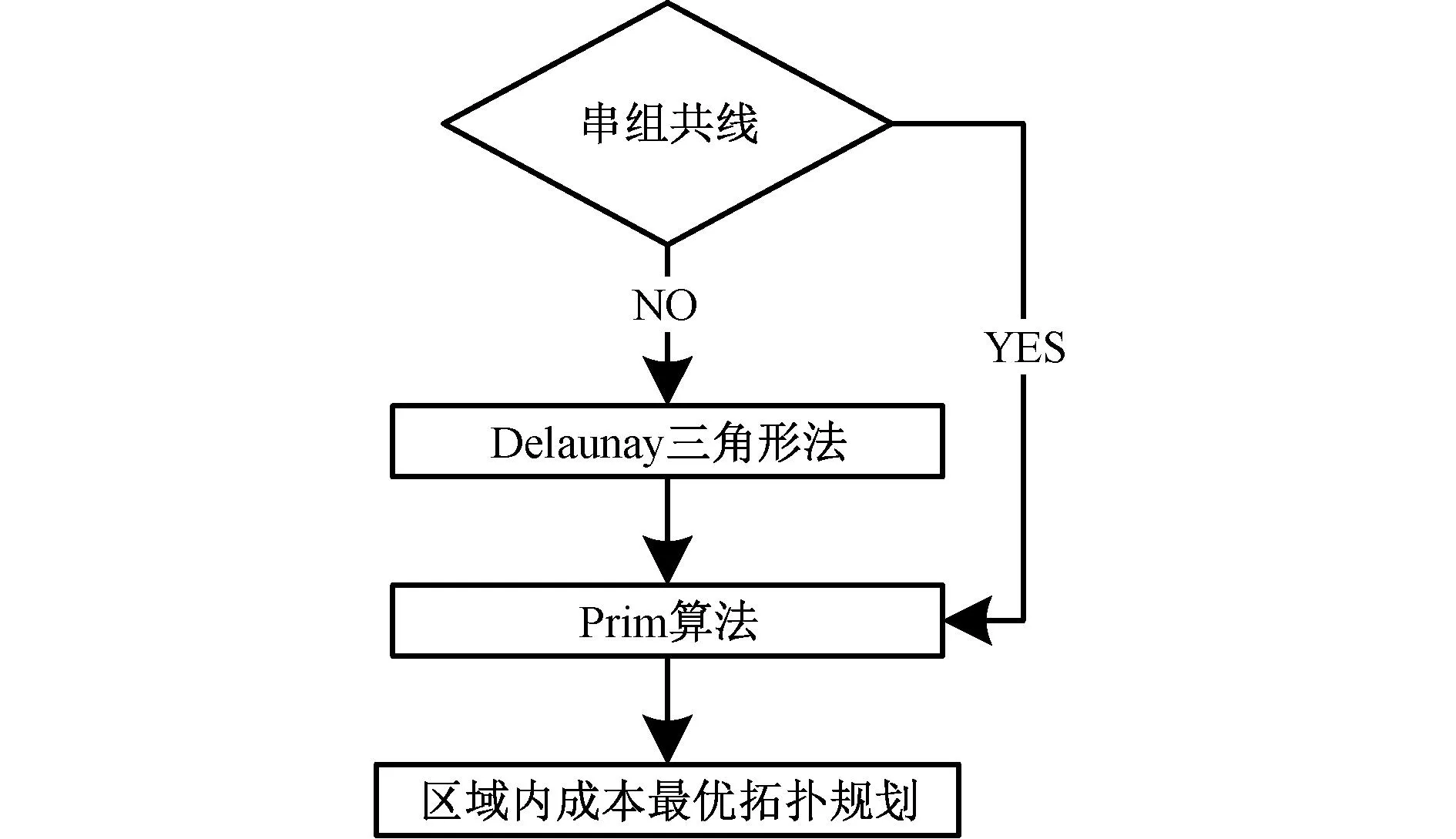
图7 Prim算法初始路径选取流程图Fig.7 Flow chart of Prim algorithm initial path selection

如图8所示,Delaunay三角剖分法具有空圆特性,三角形网中各三角形的外接圆内无顶点,可直接选取满足海缆布线不交叉的有效路径。串组顶点数量不足3个或顶点共线无法构造Delaunay三角形,上述情况不存在无效路径,直接进行成本最优拓扑规划。

图8 Delaunay三角剖分法线路选取图Fig.8 Route selection diagram of Delaunay triangulation method

Prim最小树的权值设置为距离,所得的最小树为电缆长度最小,并不是电缆总成本最小树,为了获得成本最优树,提出在规划前可根据潮流分布选择导线截面的改进算法。

以原最小树为基础,将串组内由Delaunay三角剖分法选取的不形成连通区域路径进行随机组合,以图9为例,例中存在节点6个,边权值为距离,依据距离最短原则,选取(a)中加黑线路径;在已选最短路径中,随机选择节点VI,将原路径删除,为形成不闭合的连通区域,需由(b)中浅虚线内选取路径;随机选取(c)中加黑粗线路径,形成新最小树,若新最小树经济性优于原最小树,则更新拓扑结构至新最小树。依据上述算法,逐次计算集电系统整体主要投资成本,选取经济性最优的拓扑结构,规划效果如图10所示。

图9 改进Prim算法原理示意图Fig.9 Schematic diagram of improved Prim algorithm

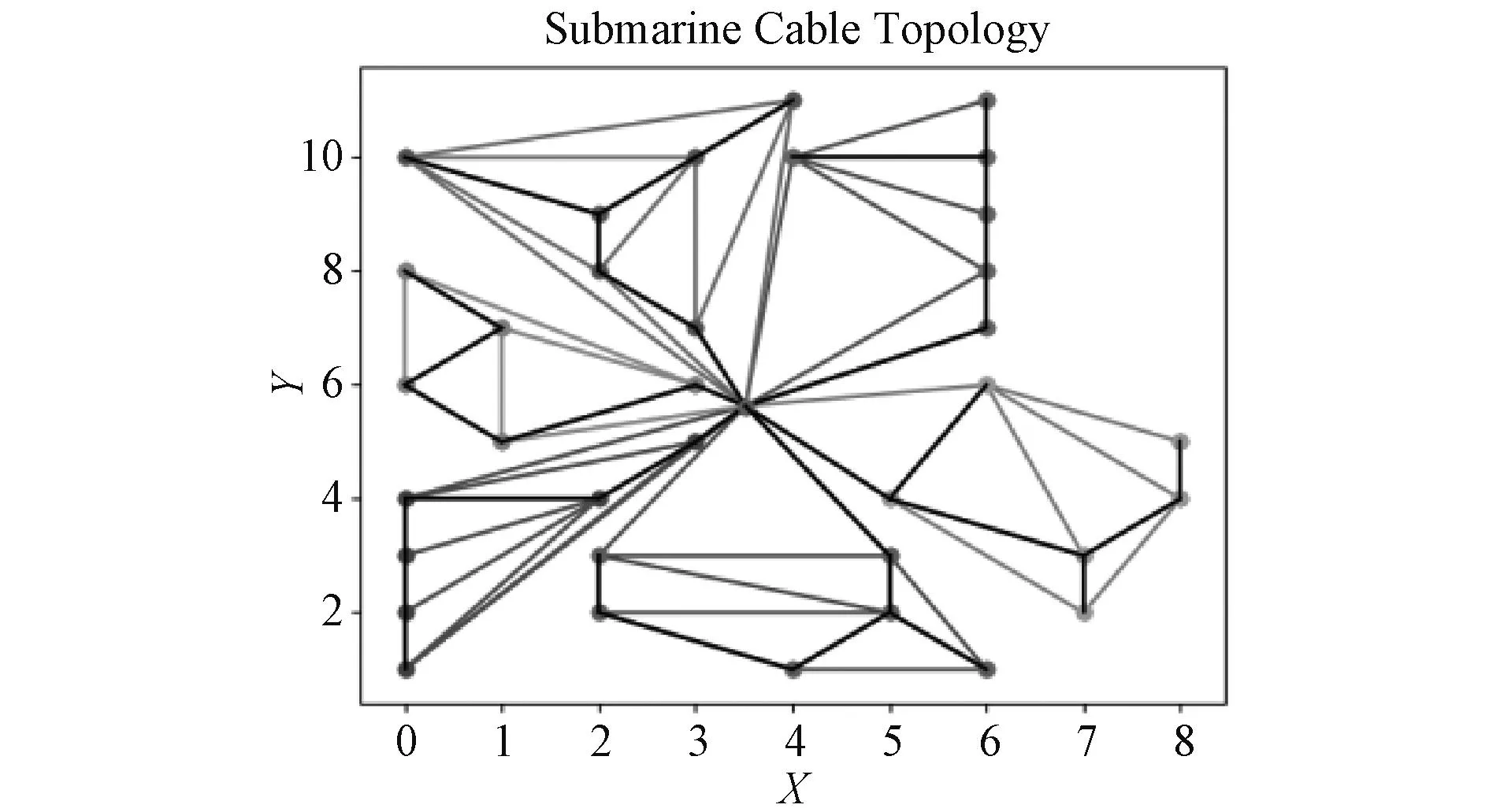
图10 最优路径选取示意图Fig.10 Schematic diagram of optimal route selection

3 算例分析

本文算例中风电机组容量设为8 MW,海缆电压等级为66 kV及35 kV,具体选型参数见表1。本文使用2种算例,其设计容量分别488 MW(算例1)、280 MW(算例2),将进行FCM算法与改进FCM算法的规划效率、寻优性及普适性对比分析。

3.1 规划效率分析

规划效率分析中,海缆的电压等级为66 kV,最大传输容量为77.8 MW,使用算例1,分别对FCM算法与改进FCM算法完成50次海上风电场集电系统拓扑优化计算,其迭代次数分布情况如图11、图12所示。由迭代次数分布情况对比可知,使用FCM算法完成集电系统拓扑优化的平均迭代次数为2 628.54次,而使用改进FCM算法完成此任务的平均迭代次数为1 458.67次,改进FCM算法较原算法的规划效率提升了近44.5%。

图11 FCM算法迭代次数图Fig.11 Plot of the number of iterations of the FCM algorithm

图12 改进FCM算法迭代次数图Fig.12 Plot of the number of iterations of the improved FCM algorithm

3.2 寻优性分析

寻优性分析中,海缆的电压等级为66 kV,最大传输容量为77.8 MW,使用算例1,分别对FCM算法与改进FCM算法完成50次海上风电场集电系统拓扑优化计算,两算法拓扑优化计算一次结果的分段海缆造价情况如表3、表4所示。

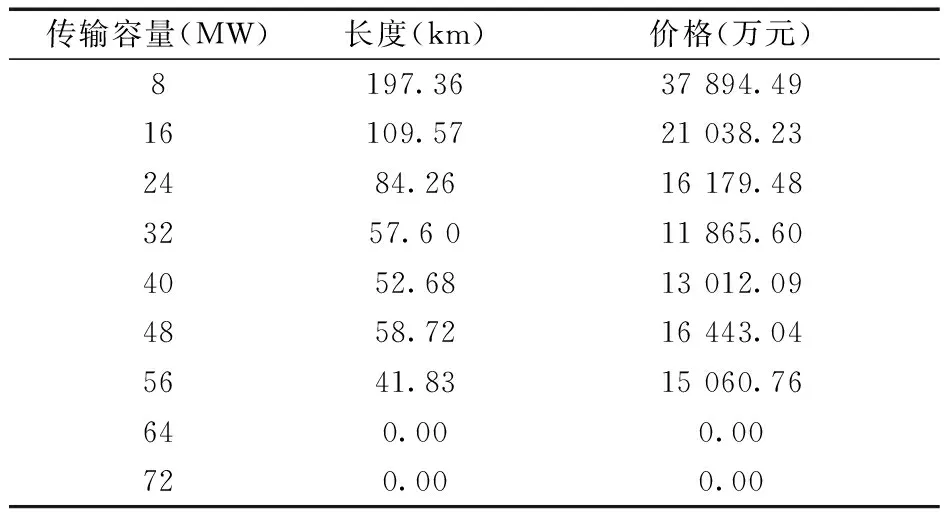
表3 FCM算法集电系统拓扑优化计算

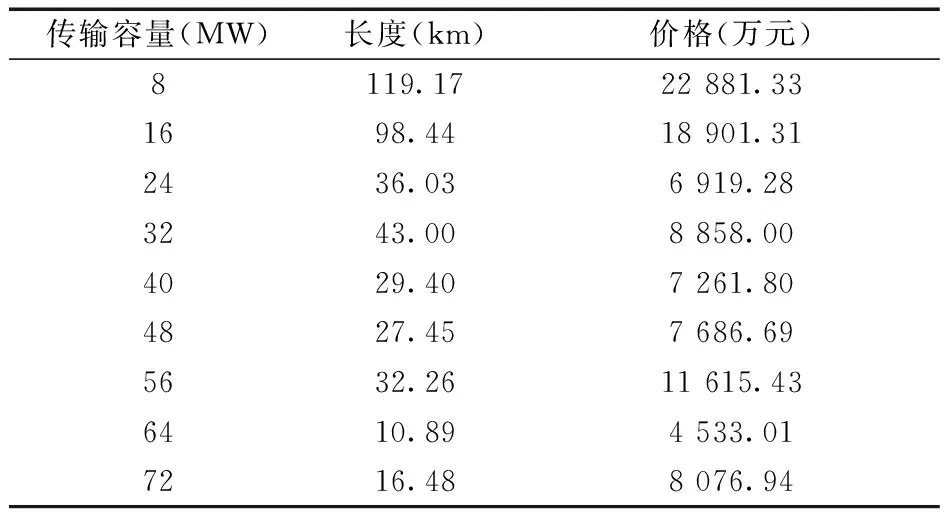
表4 改进FCM算法集电系统拓扑优化计算

其50次逐次总造价结果(包含表2中提及的海上风电场集电系统主要投资成本)分布情况如图13、图14所示。

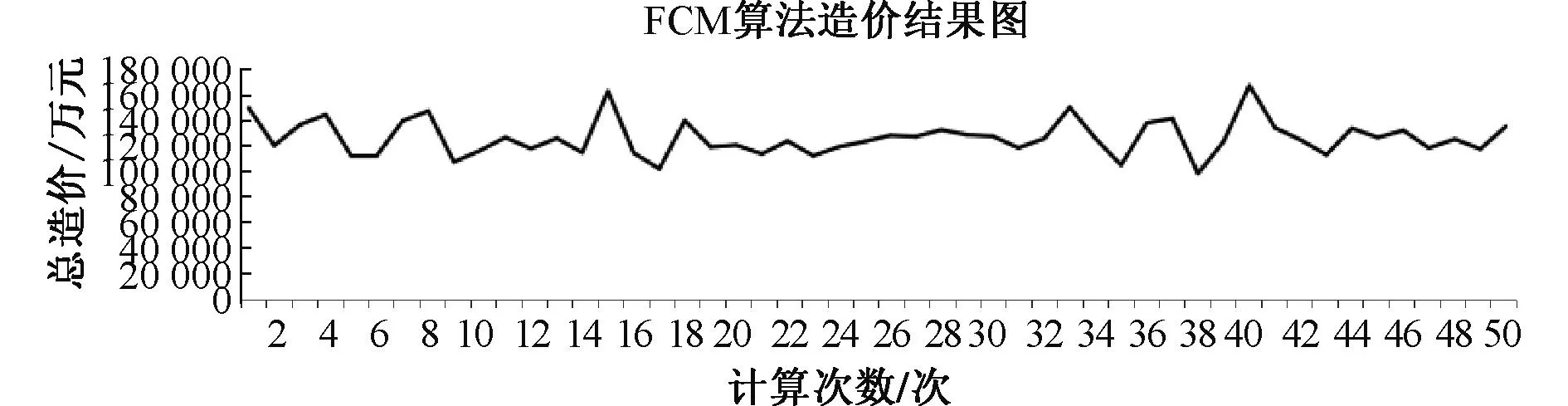
图13 FCM算法造价结果图Fig.13 Cost results diagram of the FCM algorithm

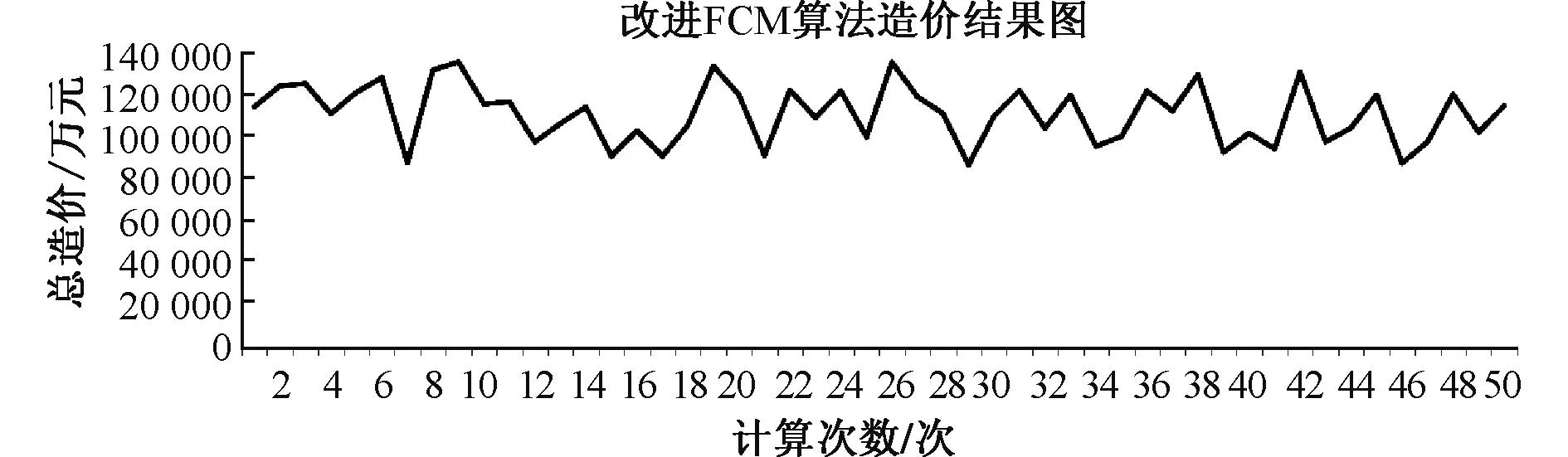
图14 改进FCM算法造价结果图Fig.14 Cost results diagram of the improved FCM algorithm

使用FCM算法完成集电系统拓扑优化的平均造价为127 947.191万元,本文提出的改进FCM算法平均造价为110 127.179万元。改进FCM算法较原算法就海上风电场集电系统主要投资成本的优化结果而言,平均减少近13.8%。

3.3 普适性分析

本节选用66 kV及35 kV两种电压等级的海缆,并使用算例2。

降维分区机制主要依据风机的空间位置,不同电压等级海缆下的海上风电场集电系统对于降维计算无本质区别,本身具有一定的普适性。在改进算法结构后,可有效解决大型风机海上风电场集电系统拓扑优化在选取集电系统电压等级较低时,串组内风电机组个数冗余度受限、集电系统拓扑结构更加复杂导致降维分区寻优性降低或规划失败的问题。

如图15所示,本文方法可完成不同海缆电压等级、不同规模海上风电场的集电系统拓扑优化,结合第2节所述算法机制可知,改进FCM算法对于大型风机海上风电场集电系统拓扑优化具有良好的普适性。

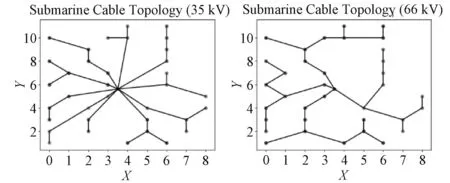
图15 不同电压等级海缆下的拓扑优化结果图Fig.15 Topology optimization results of submarine cables with different voltage levels

4 结 论

本文从集电系统拓扑优化模型、改进FCM算法设计角度介绍了大容量风电机组的海上风电场集电系统拓扑优化,并从内外循环结构、补充隶属度算法、串组位置关系判断及改进Prim算法经济性寻优等结构设计方面分析了算法改进对于提高集电系统拓扑优化性能的原理,结合算例证明了本文算法对于大型风机海上风电场集电系统拓扑优化具有良好的规划效率、寻优性及普适性。

本文采用的集电系统拓扑结构为放射形结构,而实际工程中可能出现复合环形、双边环形等不同结构,未来将就不同拓扑结构的优化组合方式及其经济性进行深入研究。