基于改进DTW 算法的高维时空数据关联挖掘方法
周春雷,董新微,季 良,张璧君,许中平
(1.国家电网有限公司大数据中心,北京 100052;2.安徽继远软件有限公司,安徽合肥 230088;3.北京国网信通埃森哲信息技术有限公司,北京 100052)
与传统电网不同,智能电网通过分析分布式测量设备(例如:电力测量单元、变电站、发电机、储能系统和智能电表)收集的大量数据,为电网运行提供新的以数据为中心的服务。随着电网智能化水平不断提高,监测电网运行状态、电能质量、设备运行状态等过程中产生了大量高维时空数据。但是由于数据存在冗余和缺失等,所以要对电力系统的空间和时间数据进行挖掘和分析。
目前,有学者提出利用区块链方法评估电网节点数据时空关联特性。该方法挖掘了电压相量轨迹信息几何特征,构建轨迹运动演进规律的特征平面,并通过轨迹距离密度设计的参数自适应聚类算法,评估了节点相似性[1]。但该方法在处理大量数据时,效率和运算速度都较慢。还有学者提出基于Apriori关联规则算法,其先对各个波段进行分析,然后再利用这些波段来生成更强的相关关系。应用Apriori关联规则算法,首先扫描多个数据库,然后生成大量常用的候选对象,从而使得Apriori 算法具有时间和空间上的复杂性[2]。其在挖掘大量数据时,性能有待完善。在大数据时代,传统的时间—空间轨道数据关联的方法,已无法适应对数据的快速关联和数据挖掘的要求,同时也存在着较大的不足。为此,提出了基于改进DTW 算法的高维时空数据关联挖掘方法。
1 高维时空数据关联性判断
1.1 空间数据关联性判断
从空间梯度特征来看,电网节点间的空间关联性通常是,在某一时刻邻近节点之间的感知数据相同或相似。在对簇头和簇内部数据进行拟合时,其错误率低于所规定的阈值[3]。利用两个节点的历史感知数据挖掘出两个节点关系,可以判断出簇内的节点与簇的空间关联[4]。该方法无须传输节点的感知数据,只需将相关模式发送给聚集节点,即可在不进行节点感知数据的前提下,将感知到的数据恢复到集群中。
为了保证在一定时间序列下,簇头节点oi和簇内节点sj均为连续的历史数据,这两个节点空间相关性判断步骤为:
步骤1:计算两个节点形成的差值序列,公式为:
由式(1)可确定,簇头节点oi和簇内节点sj产生的差值序列[5]。
步骤2:根据式(1)计算两个节点差值序列,构造簇节点的原始序列,可表示为z;
步骤3:根据均值分析两个序列拟合误差,公式为:
式中,m表示计算次数。
步骤4:如果拟合误差小于给定的误差阈值,则判定两个节点的数据存在空间关联性[6];反之,则不存在关联性。
1.2 时间数据关联性判断
高维时空数据具有周期性变化规律,从单一节点获得的感知数据,可以作为基于采样时间的自变量,而由变数分段线性关系得到的感知数据,可以视为以采样时间为基础的因变量[7]。
在拟合回归线附近,将感知数据按时间序列分布。利用线性回归方法,建立了一种基于线性回归的时间数据关联性判断模型,如图1 所示。
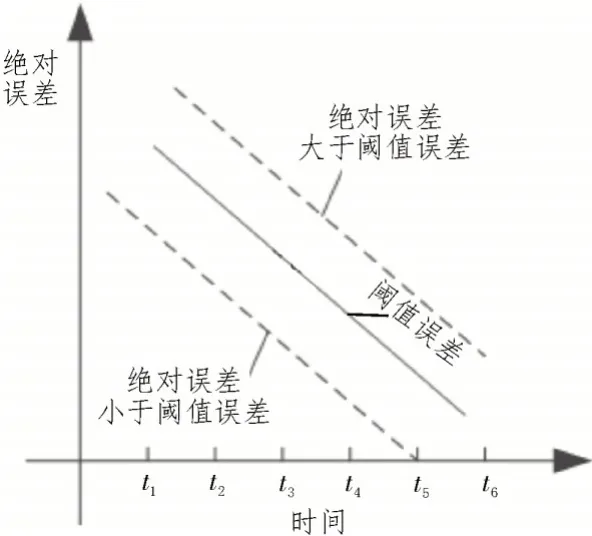
图1 基于线性回归的时间数据关联性判断模型
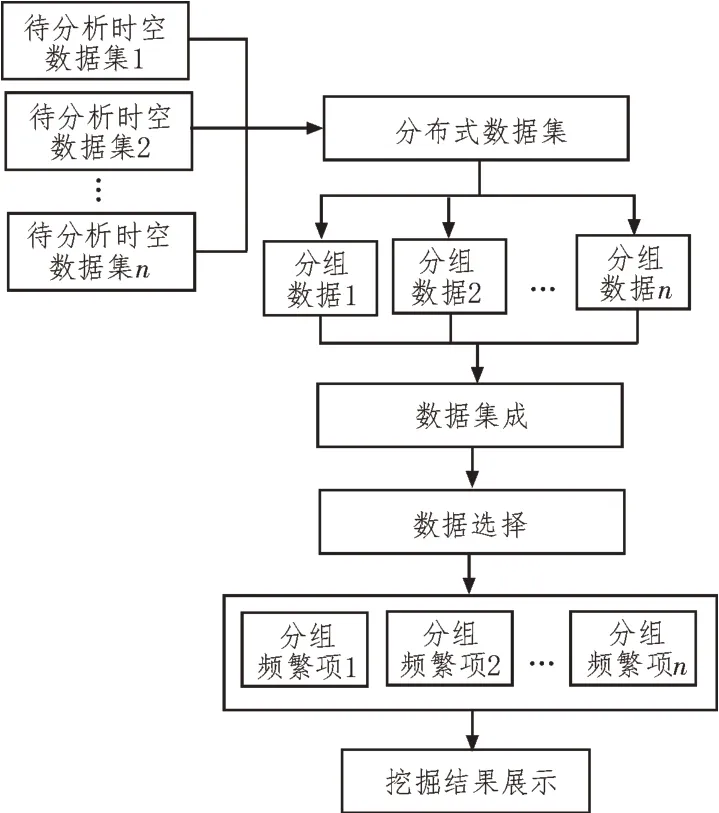
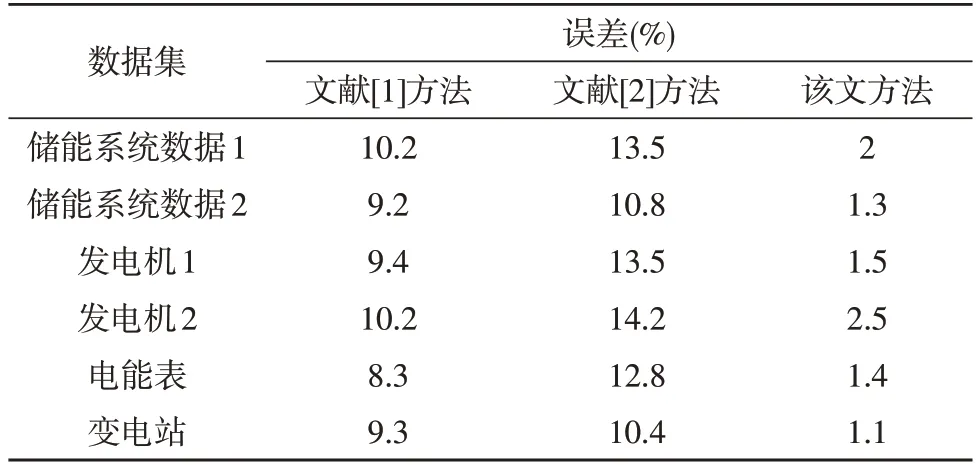
图1 中,设节点的感知数据与实际数据绝对误差为μ,阈值误差为e,如果μ 利用改进的DTW 算法对高维时空数据进行离散,获得多个层次的模糊集合,并建立了一个模糊数据库[10]。采用改进DTW 算法生成频繁项集,以此为依据挖掘高维时空数据关联性。 对于需要预处理的高维空间数据,利用该数据作为参考依据,使用改进DTW 算法实现了等距离同步处理[11]。详细步骤为: 在同一维度上,计算空间数据L1和时间数据L2之间的距离,公式为: 式中,wi表示两组数据间的欧氏距离值[12]。 在搜索区间内,依次计算出距离矩阵累计结果,其公式如下: 式中,i、j分别表示第i个和第j个采样。根据计算结果继续搜索,选择其中最小值,并将其对应的数据依次标记,获取高维时空数据预处理结果。 在高维时空数据挖掘中,可以通过时间与空间的关系生成频繁项目集,通过最小集合周期生成频繁项目集[13]。然后对DTW 方法进行修改,以进一步提升数据挖掘的准确性。详细关联挖掘过程如图2所示。 图2 关联挖掘过程 由图2 可知,结合改进DTW 算法,极大提升了高维时空数据关联挖掘速度,详细步骤如下所示: 步骤1:构建高维时空数据集 由于改进的DTW 算法在关联挖掘过程中需要经过大量的计算步骤,占用了大量的存储空间[14-15],因此,为了解决这一问题,设计了高维时空数据关联挖掘路径,如图3 所示。 图3 关联挖掘路径 如图3 所示,将高维数据分为三维,分别是一维[1,x1]、二维[x1+1,x2]、三维[x2+1,x3]。对于x1和x3值的计算可表示为: 式中,r表示采样点数;α表示平行四边形相邻两边一侧的斜率;β表示平行四边形相邻两边另一侧的斜率。当挖掘数据不在平行四边形内部时,说明这些数据不具有关联性,无需挖掘;反之,则具有关联性,可以挖掘。根据挖掘结果,集合高维时空数据集[16]。 步骤2:扫描所有的数据集,并记录每次数据出现的次数。依据需求定义,判定时间和空间数据是否处于相同的维度,若存在,则将其记录于项头表中; 步骤3:循环数据集,删除不在项头表中的数据,并按项头表的增加次序排列数据。重新循环数据集后,在产生的频繁模式树中,所有的节点都表示高维度的空间和时间数据,而树枝表示高维时空数据出现的次数; 步骤4:在循环项头表中,按递减次序的条目,查找经常模式树中的条目和条目的树叶节点,并剔除重复节点数据,获得一个单独的树结构数据集,此时的数据集就是一个具有关联性的集合[17]。 步骤5:将所有单一路径的树状结构数据集输出,构成最终结果集。 步骤6:将上一步骤的最终结果集作为模糊属性集,基于原始数据库建立模糊数据库。设空间数据为空间数据L1的支持度,时间数据为时间数据L2的支持度。规则L1⇒L2在数据库K中的支持度可表示为: 由式(6)可知,在模糊关联关系中计算模糊支持度,即蕴涵度,能够有效减少挖掘步骤,缩短挖掘所用时间。第h个数据蕴涵度可表示为: 式中,FIO 表示蕴涵度算子。 通过计算支持度,能够确定频繁项集,该结果即为高维时空数据的关联挖掘。 为了验证基于改进DTW 算法的高维时空数据关联挖掘方法的有效性,在Matlab 平台上通过Unix操作系统进行实验测试。 为了使实验结果更加明显,以某电网数据为例,对每个时间序列进行了扩充,得到6 组时间序列,并且从序列第一个数据点开始采集,采集变电站、发电机、储能系统和智能电表等不同时空节点数据。在数据集中,对时空序列依次进行相似度检索,为实验提供数据支持。 关联挖掘误差计算公式如式(8)所示: 式中,d表示挖掘次数;vc表示数据未被搜索到的信息。该计算结果值越大,说明高维时空数据关联挖掘结果越精准。 分别使用电网节点时空关联特性评估方法(文献[1]方法)、基于Apriori关联规则算法(文献[2]方法)和基于改进DTW 算法的关联挖掘方法(该文方法)进行数据挖掘。三种方法的挖掘误差结果如表1所示。 表1 数据挖掘误差对比分析 由表1 可知,文献[1]方法的平均挖掘误差为9.4%,文献[2]方法的平均挖掘误差为12.5%,该文方法的平均挖掘误差为1.6%。因为该文方法在数据预处理过程中先明确了数据距离矩阵累积结果,并计算空间数据和时间数据的支持度并与设定的阈值对比,从而降低了数据关联挖掘误差。 文中提出的基于改进DTW 算法的高维时空数据关联挖掘方法,通过计算蕴涵度确定数据之间的支持度,结合改进DTW 算法挖掘高维时空数据关联性。通过实验证明,该方法可以有效提高数据挖掘的完整性,减少误差。然而该研究仍处于单层关联性方面,为了扩展该方法的应用领域,后期将致力于多层关联性的研究应用。2 改进DTW算法下高维时空数据关联挖掘
2.1 高维时空数据预处理
2.2 高维时空数据关联挖掘过程

3 实 验
3.1 实验数据集
3.2 实验指标确定
3.3 实验结果与分析
4 结束语

