考虑行进避障的巡检机器人编队队形自动控制方法
朱玺
(国网上海市电力公司信息通信公司,上海 200040)
机器人的编队控制是保证其正常运行的首要技术机制,不仅能应用于日常行走、侦察,还能进一步进行空间探测、搜救、巡逻等高难度工作。但由于日常作业涉及的数据量过于庞大,且天气、人为以及障碍物影响等意外因素过多,导致编队队形难以实现有效精准的控制。
文献[1]采用深度学习方法建立奖励值模型,采集现场数据作为模型的初始输入值,根据不同的编队理念构建不同的神经网络结构,在不同的任务场景下,求解输出最优的控制函数,完成控制。该方法所需的数据量较大、耗用量较高,整体实用性不强。文献[2]分析现场多传感信息数据,选择存在障碍和不存在障碍另种编队数据集,融合数据集同种特征数据,求得相关控制参数。该方法进行特征融合时,容易忽略噪声因素影响,导致控制值和实际值差值过大,控制效果较差。针对上述问题,提出了一种考虑行进避障的巡检机器人编队队形自动控制方法。
1 机器人运动学模型构建
要提高巡检机器人编队队形自动控制方法的精准性,需要对机器人的运动模型进行分析,了解其运动模式、正常行走的状态向量以及运行速率等参数,这些参数可以作为后续自动控制的参照,尽可能降低判定误差。将机器人的运动作为一种空间内的二维运动,将三维运动抽象为二维运动,采用二次积分模型[3],对机器人运动学涉及的各个参数进行描述,表达公式为:
式中,x表示机器人R的初始位置;v表示机器人R的速度值,v∈R;x′表示抽象表达[4]后的位置值;m表示机器人质量。将机器人在二维方向上检测到的障碍物质点抽象为具有单位质量的质点[5],此时,机器人R的实时状态向量值为:
推导求得机器人R的状态方程为:
式中,O、I分别表示对应维度的单位矩阵和零状态矩阵。
一般情况下,由于机器人自身存在驱动约束[6],运动速度也存在上限值,在出现意外情况时能保证机器人的有效制动。参考这种情况,计算机器人行进速率上限值和编队队形的速率均值[7],求得二者之间的均值v′作为自动控制的参照值,提升自动控制精准度,计算公式为:
式中,a(t)表示时间参数;vmax表示机器人的最大速率值。
2 运动稳定性分析
如何在编队过程中保证机器人的稳定,也是自动控制算法需要考虑的重要因素之一。该文针对该问题,参考机器人的稳态运动理论,进行相关讨论如下:
设机器人的参考节点为M,跟随机器人的运动特点,采用线性的方式将其运动特点描述为:
式中,f表示线性参数[8];k1表示稳定点;k2表示动态变换点;γ表示直线运动点;λ表示曲线运动点。结合机器人直线和曲线的两种运动状态,得到平衡点的计算公式为:
式中,e表示收敛系数[9];表示编队队形的平衡差
3 机器人编队队形自动控制实现
考虑到机器人在编队过程中容易受到的障碍物碰撞影响,提出结合惩罚因子[10]的概念来设计编队队形的自动控制方案。惩罚因子属于约束队形路径长度的系数,计算公式为:
式中,β代表惩罚因子;d0代表巡检机器人与障碍物之间的标准安全距离[11];d′代表巡检机器人与障碍物间的距离最小值;ρ0代表编队队形涉及的最大范围,π 表示编队中心运动轨迹。
假设编队队形的最短路径长度[12]为l,考虑行进避障的情况,得到最为安全的编队路径长度o为:
当0 ≤d′<ρ0+d0时,说明编队路径与障碍物之间的距离较近,不在安全距离内,此时,编队路径选择为不安全路径,惩罚因子β的数值变大,l变大;当0 ≥ρ0+d0时,代表编队路径与障碍物之间的距离较远,属于安全距离内,此时,惩罚因子β数值变小为0,l也随之变小。将上述关系通过图像进行描述,如图1 所示。
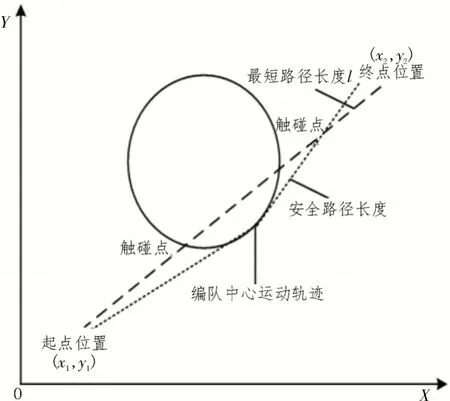
图1 机器人编队中心运动轨迹
从图1 中可以看出,x2>x1,障碍物的位置坐标为(a,b),编队路径关系为0 ≤d′<ρ0+d0,公式为:
式中,(x1,y1) 表示编队路径起始位置;(x2,y2)表示编队终点位置。计算两点间最短的编队路径长度l为:
在实际应用中,可将路径问题直接转换为编队中心与障碍物之间的安全距离()ρ0+d0问题,求得与障碍物之间的交点坐标值[13]为:
式中,a、b均表示机器人样本集。当整个机器人编队到达目标点时,此时与障碍物之间的最短安全距离为:
得到惩罚因子β为:
为保证编队队形自动控制的精准性,根据上述过程求得的惩罚因子和避障的最佳路径建立目标函数为(l,l′) →0,(κ,κ′) →0,其中,l′表示避障路径自动控制系数;κ′表示最佳控制比例系数[14];κ表示控制变量[15-16],推导求得最终的自动控制函数为:
式中,κ(x)控制函数;μ表示线性控制变量系数。通过上述步骤,由此完成巡检机器人编队队形自动控制。
4 实验分析
4.1 实验设置
为了验证考虑行进避障的巡检机器人编队队形自动控制方法的有效性,在巡检机器人编队队形自动控制实验中,挑选六个巡检机器人在未知的环境中进行行进、巡检等运动,保证其在一段时间内能够维持队形运动至预先指定位置。在整个实验过程中,还设置了不同类型的障碍物,分别为扩散型障碍物、动态障碍物、狭窄通道障碍物以及复杂形态障碍物。将这些障碍物分别布置在测试环境中的不同位置处,以便检测编队控制算法避障能力[17-18]。
实验所用机器人预先设定的位置误差为3 cm,即进行测试时,实际与预期误差小于3 cm 时,则判定机器人在队形中。实验所需详细参数表示如表1所示。

表1 实验所需详细参数
4.2 巡检机器人编队队形自动控制效果对比分析
该实验的验证方法主要根据机器人的避障及编队控制问题进行验证,一方面检测编队控制算法的避障能力,另一方面检测算法的协调能力。为提高实验结果的参考能力,将设置三组实验分别为三种障碍物编队、菱形障碍物狭窄通道编队以及六边形障碍物编队,并与文献[1]方法、文献[2]方法进行对比分析。在Matlab 上搭建了测试平台,编队自动控制结果如图2 所示。其中,黑色实心的任意几何图形代表障碍物,空心圆圈代表机器人起始点和终点位置,各种线条代表不同方法的编队路径。

图2 编队自动控制结果
从图2 中可以看出,无论是在哪种障碍物环境中,所提方法的编队队形路径最短且与障碍物之间的误碰率最低,路径曲线平整度最高且没有出现过多的折叠弯曲现象,而另外两种方法都出现了故障碰撞现象。这说明,在进行编队队形自动控制时,所提方法控制效果较好,避障能力较强,可以保证机器人在整个运动过程中速度变化的平稳能力,避障轨迹较为平滑,即使在狭窄的菱形障碍环境下,也能在第一时间恢复队形,达到高效自动控制。
4.3 自动控制误差对比分析
进一步验证所提方法的巡检机器人编队队形自动控制误差,该误差值代表机器人在进行编队队形控制时,控制的实际点位与预期点位之间的距离差值,通过距离差值,实现自动控制有效性的精准判定。三种方法对于巡检机器人编队队形自动控制误差对比曲线如图3 所示。
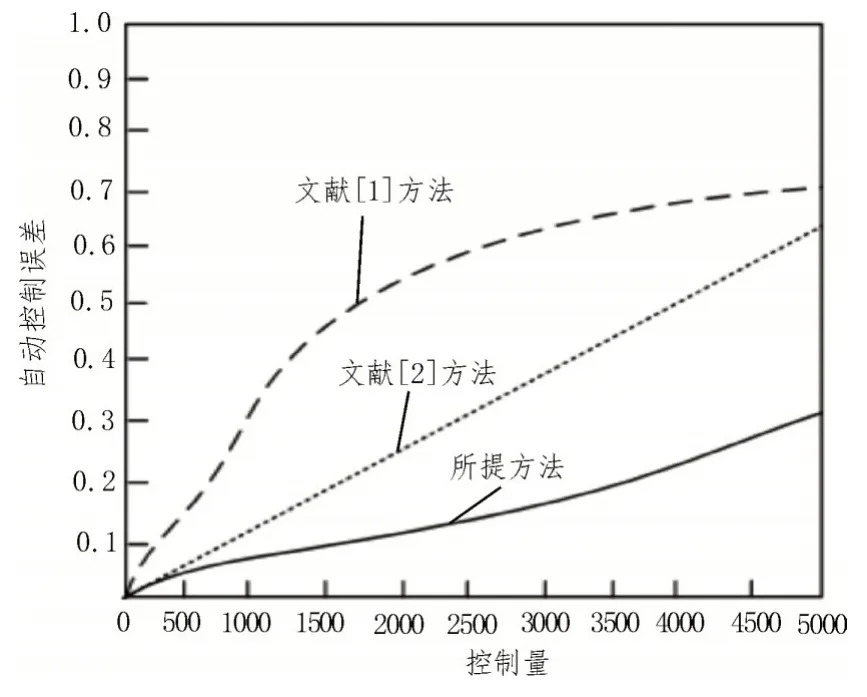
图3 三种方法自动控制误差对比曲线
从图3 中可以看出,所提方法的控制误差和曲线分布范围较低。随着控制量的增长,误差曲线没有出现大幅度上升。当控制量达到5 000 时,所提方法的自动控制误差为0.32。而另外两种方法的曲线分布明显较高,误差曲线上升幅度较大。当控制量达到5 000 时,文献[1]方法和文献[2]方法的自动控制误差分别为0.71 和0.63。由此可知,献[1]方法和文献[2]方法不能很好地消化较大的控制量,控制精准性较低,误差较大。
5 结论
针对巡检机器人环境干扰量过大导致的编队队形控制效果差、误差大的问题,提出了考虑行进障碍的机器人编队队形自动控制方法。对机器人的运动学模型进行了系统的分析,捕捉可能影响运行稳定性的关键参数。了解机器人遇见障碍物的特征因子,最大程度解决障碍影响问题。该方法的编队队形控制效果较好,确保控制质量,减小控制误差。

