大场景光学运动捕捉系统标定方法研究

罗豪龙，李建胜，邹丹平，杨子迪，李广云

（1 战略支援部队信息工程大学 地理空间信息学院，郑州 450001）

（2 上海交通大学 上海市北斗导航与位置服务重点实验室，上海 200240）

0 引言

光学运动捕捉系统是一种用于跟踪和捕获目标动作，并实时获取目标6 自由度运动信息的设备。随着室内高精度导航定位等技术领域的飞速发展，光学运动捕捉系统在医疗康复、运动检测、目标跟踪、场景动画、虚拟现实等方面发挥着越来越重要的作用［1-4］。目前主流的光学运动捕捉系统如Vicon 运动捕捉系统、Optitrack 运动捕捉系统等标称精度能达到毫米甚至亚毫米级，在室内导航领域为无人机、无人车导航感知提供真实的位置和姿态信息［5-7］。然而在实际使用中，由于场地震动、运动捕捉系统的相机数量、运动捕捉系统的空间分布和噪声等因素的影响，光学运动捕捉系统的实际定位精度往往远低于厂家的标称精度。尤其是大场景下，受到实际场地和空间布局的限制，光学运动捕捉系统的覆盖范围大，往往存在相机分布分散、共视区域的相机数量少、相机与目标距离远等诸多实际问题，导致光学运动捕捉系统的定位精度严重降低。如果光学运动捕捉系统的实际定位精度与标称精度相差过大，运动捕捉系统的性能将大打折扣，难以发挥运动捕捉系统的实际作用。因此，研究如何准确标定实际场景尤其是大场景下光学运动捕捉系统的定位精度，对于保证光学运动捕捉系统高效、准确、稳定的运行，根据实际场景选择配套方案的光学运动捕捉系统和拓展光学运动捕捉系统的应用场景具有重要价值和研究意义。

国外，针对光学运动捕捉系统定位精度的研究主要集中在医学生物领域。AURAND A M 长时间多次测量同一个点，利用重复定位精度评估光学运动定位系统的重复定位精度［8］；VAN DER KRUK E 对包括运动捕捉系统、实时动态（Real-Time Kinematic，RTK）载波相位差分定位系统、射频识别（Radio Frequency Identification，RFID）定位系统等17 种定位系统的研究进展进行了梳理总结［9］；WINDOLF M 在180 mm×180 mm×150 mm 小空间下对Vicon-460 的系统精度进行了检测，缺点在于检测范围过小，难以反映实际场景中系统的定位精度［10］。国内，杨治铎利用地面网格作为真实值对光学运动捕捉系统的定位精度开展研究，但是地面网格的精度难以保证［11］；谭菁华利用千分尺通过距离测量的方式检测光学运动捕捉系统的定位精度，存在的问题在于千分尺的测量范围太小，不能用于实际场景中光学运动捕捉系统的精度检测［12］。此外，国内学者更多是将光学运动捕捉系统的定位结果作为真实值对其他定位系统进行标定［13-14］。如刘智伟利用光学运动捕捉系统实现了超宽带（Ultra Wide Band，UWB）系统的精度标定，但是对光学运动捕捉系统本身的定位精度检测缺乏研究［15］。

目前学者主要在小空间内检测光学运动捕捉系统的定位精度，且往往采用重复轨迹精度的方式评估系统的定位精度，不能真实反映实际场景尤其是大场景下光学运动捕捉系统的实际定位精度［16］。因此，为了获取实际场景尤其是大场景下光学运动捕捉系统的实际定位精度，本文提出一种大场景下光学运动捕捉系统的标定方法。利用全站仪和光学运动捕捉系统进行公共点测量获取公共点的真实值和测量值，基于罗德里格矩阵的抗差最小二乘迭代方法进行公共点转换，实现光学运动捕捉系统的精度标定。同时，基于该方法实现了不同光学运动捕捉系统间的外参标定。

1 光学运动捕捉系统定位原理

1.1 系统构成

光学运动捕捉系统由多个发射红外光的高速摄像机组成，光线经反光标记（marker）球反射红外光并获取其二维图像，利用三维重建原理计算marker 球的三维空间坐标数据。多个marker 球与跟踪目标固连建立刚体，可以实时获取刚体的6 自由度位置和姿态。本文所用的光学运动捕捉系统为英国Oxford Metrics Limited公司生产的Vicon 光学运动捕捉系统，Vicon 光学运动捕捉是目前主流的光学运动捕捉系统之一，具有低延迟、采样精度高等优点。Vicon 系统包括光学摄像机、Vicon Tracker 运动捕捉软件、数据采集器、信息转换盒、T 型校正架、L 型标定直角尺和专用连接线等。镜头间采用并联连接方式保证单个镜头独立工作，确保单镜头出现故障时不影响系统正常工作。某高校大型测试场布设的光学运动捕捉系统相机配置如表1 所示。

表1 Vicon 系统相机配置Table 1 Vicon system camera configuration

1.2 定位原理

Vicon 运动捕捉系统由多个相机组成的定位系统，系统定位原理为立体视觉的三维空间定位原理。图1所示为世界坐标系Ow-XwYwZw、相机坐标系Oc-XcYcZc、图像坐标系Oi-xy和像素坐标系O-uv的对应关系，其中Ow、Oc、Oi和O分别为三个坐标系的原点。

图1 坐标系对应关系Fig.1 Coordinate system correspondence

图2 所示为双目立体视觉的三维空间定位原理。假设空间三维点Pw（xw，yw，zw）在左右目相机的像素坐标系下坐标分别为（u1，v1）和（ur，vr）。根据坐标系间的转换关系［17］，有

图2 双目立体视觉的三维空间定位原理Fig.2 Three-dimensional spatial positioning principle based on binocular stereo vision

式中，Κl，Kr为左右目相机内参，Tl，Tr为世界坐标系下左右目相机系的位姿，zl，zr表示点在左右目相机坐标系下的Z轴方向坐标。根据式（1）、（2），可以解算空间点Pw的三维位置坐标。

2 光学运动捕捉系统标定原理

本文利用全站仪进行光学运动捕捉系统的精度标定。测量原理为全站仪和光学运动捕捉系统测量若干公共点，全站仪的测量结果作为真实值，光学运动捕捉系统的测量结果作为测量值，通过公共点转换的方式实现二者系统坐标系的统一，并计算光学运动捕捉系统的实际定位精度。光学运动捕捉系统的定位精度标定原理如图3 所示。

图3 光学运动捕捉系统标定原理Fig.3 Calibration principle of optical motion capture system

2.1 全站仪测量原理

全站仪是一种由电子经纬仪、光电测距仪和数据处理系统所组成的高精度测量仪器，它将光学、机械和电子技术相结合，集成水平角、竖直角、距离和高差等多个测量功能于一身。全站仪采用光学测量原理，利用激光束对目标点进行测量，通过接收反射回来的信号，测量目标点与全站仪之间的水平角度、垂直角度和距离等信息，并借助内部软件计算出目标点的三维坐标。目前，全站仪广泛应用于地形测量、矿山勘探、变形监测等多个领域。本文所用的全站仪为Leica MS60 全站仪，Leica MS60 具有测量、扫描和自动照准的功能，技术参数如表2 所示。

表2 全站仪技术参数Table 2 Technical parameters of total station

全站仪的测量原理如图4 所示。全站仪记录水平角和垂直角和测站点到目标点的距离S，根据测量的水平角α和垂直角θ，计算得到目标点的三维坐标为

图4 全站仪测量原理Fig.4 Measuring principle of total station

2.2 公共点测量原理

光学运动捕捉系统的测量区域均匀选取若干测量点作为公共点，全站仪和光学运动捕捉系统分别对公共点进行观测，光学运动捕捉系统测量的公共点坐标作为观测值，全站仪测量的公共点坐标作为真实值，通过坐标系统一并计算光学运动捕捉系统的实际定位精度。然而，由于光学运动捕捉系统测量的为maker 球球心，全站仪测量的是棱镜几何中心，二者测量的点非共心，即非公共点。因此，如何选取合适的测量装置，实现两个系统的公共点统一是测量的难点。为解决测量点不一致的情况，利用Leica 系列半径为19.05 mm的CCR1.5 靶球和同尺寸半球形摄影测量反光工件分别替代全站仪的常规棱镜和光学运动捕捉系统的marker 球。由于摄影测量反光工件和全站仪靶球半径相同，且摄影测量反光工件球心和全站仪靶球球心重合，因此全站仪测量的靶球球心和光学运动捕捉系统测量的摄影测量反光工件球心是相同测量点，达到了两套系统测量公共点的目的。公共点测量装置如图5 所示，图5（a）为光学运动捕捉系统的常用的反光marker 球，图5（b）为全站仪棱镜，图5（c）为半球形摄影测量反光工件，图5（d）为全站仪靶球。

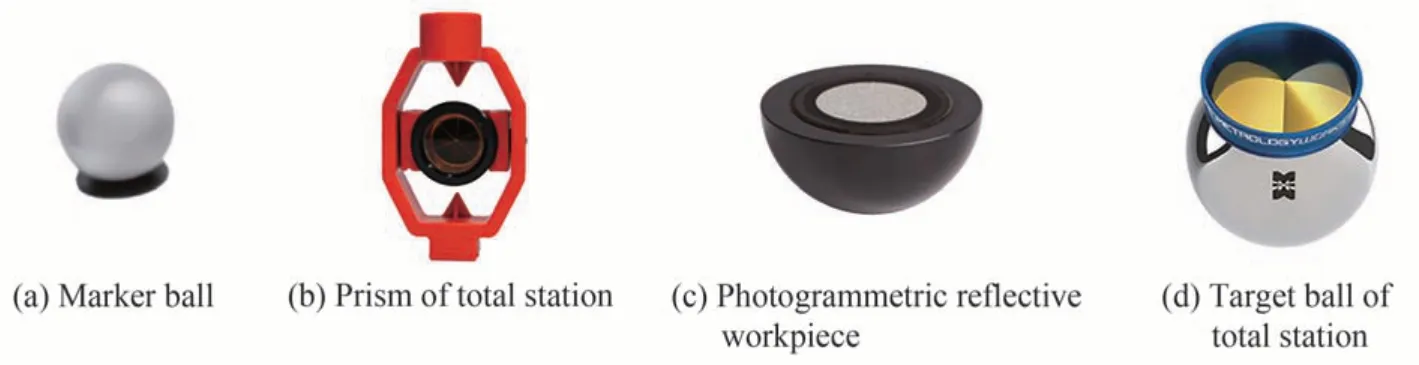
图5 公共点测量装置Fig.5 Device for measuring common points

图6 所示为公共点布设方案，根据光学运动捕捉系统的相机空间分布在四个分区域分别均匀布设若干公共点。公共点的测量过程为：1）全站仪靶球放置在公共点A位置处，全站仪测量公共点A的位置坐标；2）基座保持不动，半球形摄影测量反光工件替代全站仪靶球，光学运动捕捉系统测量公共点A的位置坐标；3）移动靶球到公共点B处，全站仪与光学运动捕捉系统依次测量公共点B的位置坐标；4）每个公共点测量三次取平均值，循环依次测量所有公共点空间位置。公共点测量原理如图7 所示。

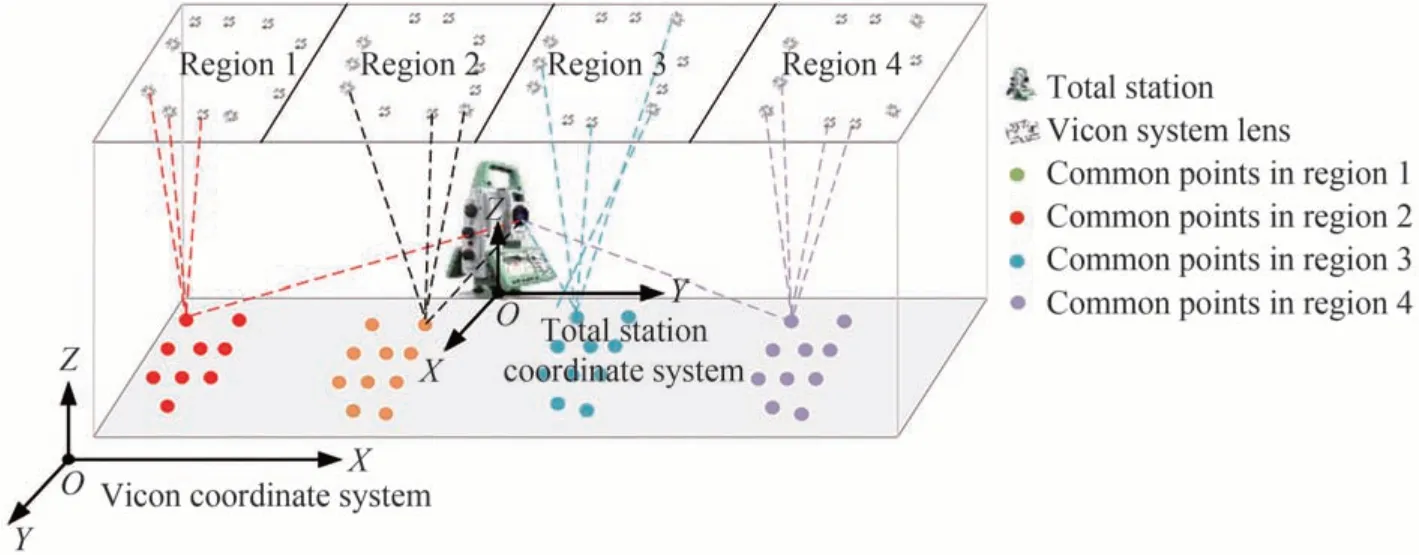
图6 公共点布设方案Fig.6 Common point layout scheme

图7 公共点测量原理Fig.7 Principle of measuring common points

2.3 坐标系转换原理

由于全站仪和光学运动捕捉系统的测量结果分别在全站仪坐标系和运动捕捉系统坐标系，二者坐标系并不统一，无法将全站仪的测量结果与运动捕捉系统的测量结果直接计算。因此，需要实现全站仪坐标系和运动捕捉系统坐标系的统一，即确定运动捕捉系统坐标系到全站仪坐标系的位姿变换矩阵。

罗德里格矩阵是由三个独立的元素组成一个矩阵，避免了象限判断的问题，利用罗德里格矩阵求解坐标系转换矩阵具有计算简单和精度高等优点［18-19］。此外，引入抗差的方法尽可能减少测量粗差对计算结果的影响，提高坐标系转换精度［20-21］。因此采用基于罗德里格矩阵的抗差最小二乘迭代方法求解坐标系转换矩阵，即运动捕捉系统坐标系到全站仪坐标系的位姿变换矩阵。罗德里格矩阵的定义为

1）引入反对称矩阵S，其中元素a，b，c相互独立。

2）定义I为三阶单位阵，则R=(I+S)(I-S)-1正交矩阵。将R展开后得到

假设某一公共点在全站仪坐标系和运动捕捉系统坐标下的坐标分别为(xi，yi，zi)T和(ui，vi，wi)T，建立二者的坐标系转换关系为

式中，R为由罗德里格矩阵表示的旋转矩阵，T为平移矩阵。

公共点作差得到

式（7）同时左乘(I-S)化简得到

令kij=ki-kj，式（8）化简为

将I、S代入，经整理得到

对于Ax=B的形式中，由于A为奇异阵，因此至少2 个方程组才能解算出a，b，c。因此，当有n个公共点时，可以得到一个3(n-1)×3 维的方程组

通过最小二乘原理计算未知数初值a0，b0，c0，根据式（5）、（6）得到旋转矩阵的初始值R0和平移矩阵的初始值T0。

由式（5）、（6）得到

线性化得到

由此得到误差方程为

其中

为避免测量粗差对参数估计的影响，引入基于IGG3 的抗差估计进行最小二乘迭代计算［22］。基于IGG3的抗差估计方法可以处理非线性、异方差等复杂情况的数据，并具有良好的鲁棒性和计算效率。该方法通过对每次观测赋予权重，并在迭代过程不断调整权重和估计参数，以减少异常值对结果的影响，达到抗差的目的。

由式（14）得到

Pi为每次观测的权因子系数，取为1。根据IGG3 中的定义，wi的形式为

式中，k0一般取1.0～1.5，k1一般取3.0～4.5，v为残差量vi与标准化残差的比值σvi。其中，标准化残差的计算方程为

式中，σv0为单位权中误差，qvi为协方差矩阵对角线上的第i个元素。单位权方差的计算公式为

式中，V表示误差项，P表示权重矩阵，m表示方程组的行数3(n-1)，t表示待估计的参数个数，取为6。

利用抗差最小二乘迭代算法计算旋转矩阵参数a，b，c和平移矩阵参数Tx，，Ty，Tz，解算得到光学运动捕捉系统坐标系到全站仪坐标系的旋转矩阵R和平移矩阵T。

2.4 光学运动捕捉系统精度检测

根据2.3 中的方法得到光学运动捕捉系统坐标系到全站仪坐标系的位姿变换矩阵和，利用式（19）将光学运动捕捉系统的测量值PV转换到全站仪坐标系下得到Pl，通过式（20）与全站仪测量的真实值PL作差得到光学运动捕捉系统在每个公共点X、Y、Z三轴方向上的测量误差，根据式（21）计算光学运动捕捉系统的点位均方根误差。

3 动捕系统外参标定方法

Vicon 运动捕捉系统和度量运动捕捉系统（NOKOV）是出自不同厂家且相互独立的光学运动捕捉系统。两个系统的空间布局如图8 所示，两个系统的相机非共视。

图8 Vicon/度量系统空间分布Fig.8 Spatial distribution of Vicon system and NOKOV system

由于室内无人机导航感知的任务要求，需要获取两套系统的外参，即实现两套运动捕捉坐标系的坐标系统一。由于度量系统和Vicon 系统的测量区域非共视，因此无法直接测量公共点计算两套系统的外参。采取的方式为利用全站仪建立统一坐标系的方法，即全站仪固定不动，利用全站仪分别在度量运动捕捉系统与Vicon 运动捕捉系统的观测区域测量若干公共点，利用2.3 中的坐标系转换方法分别计算Vicon 运动捕捉系统到全站仪坐标系的位姿变换矩阵和度量运动捕捉系统的位姿变换矩阵，进而计算Vicon 动捕系统和度量动捕系统的位姿变换矩阵，实现两套系统的外参标定。

4 实验与结果分析

图9 所示为某高校大型测试场，测试场的空间约为12 m×40 m×8 m。测试场布设一套由34 个相机镜头组成的Vicon 光学运动捕捉系统，镜头均匀分布在测试场的四个平行区域，相邻区域间包含若干个具有共视区域的相机，整个测试场组成一套完整的Vicon 运动捕捉系统。Vicon 系统软件中的俯视示意图如图10所示。在室内无人机避障导航、车机协同定位、多机协同作业等实际任务中，要求Vicon 光学运动捕捉系统为目标提供可靠的高精度定位坐标。一方面Vicon 光学运动捕捉系统为目标提供高精度定位坐标辅助目标执行导航避障等任务；另一方面Vicon 光学运动捕捉系统为目标提供高精度定位真值以验证定位导航的算法精度。然而，大场景下受Vicon 光学运动捕捉系统相机分布、相机数量以及场地振动等因素的影响，Vicon系统的实际定位精度与厂家标称的定位精度往往不符。因此，需要检验大场景下Vicon 运动捕捉系统的实际定位精度。为标定光学运动捕捉系统的定位精度，采用分区域标定和整体区域标定的方案，即分别计算四个分区域下光学运动捕捉系统的定位精度和整体区域下光学运动捕捉系统的定位精度。

图9 Vicon 系统测试场Fig.9 Vicon system test field

图10 Vicon 系统俯视图Fig.10 Vertical view of vicon system

根据Vicon 光学运动捕捉系统的分布，在Vicon 系统布设的四个区域分别均匀选取10 个空间点，Leica MS60 和Vicon 系统分别测量各区域10 个公共点的真实值和测量值，利用分区域公共点计算各分区域下光学运动捕捉系统的定位精度，利用所有公共点计算得到整体区域下光学运动捕捉系统的定位精度。图11 表示Vicon 系统标定实验，右侧上下插图分别表示全站仪靶球实验装置和半球形摄影测量反光工件实验装置，图12～16 表示系统定位精度结果。

图11 Vicon 系统标定试验Fig.11 Process of TCP calibration

图12 区域一VICON 系统定位精度Fig.12 Vicon positioning accuracy in the first area

图13 区域二Vicon 系统定位精度Fig.13 Vicon positioning accuracy in the second area

图14 区域三Vicon 系统定位精度Fig.14 Vicon positioning accuracy in the third area

图15 区域四Vicon 系统定位精度Fig.15 Vicon positioning accuracy in the fourth area

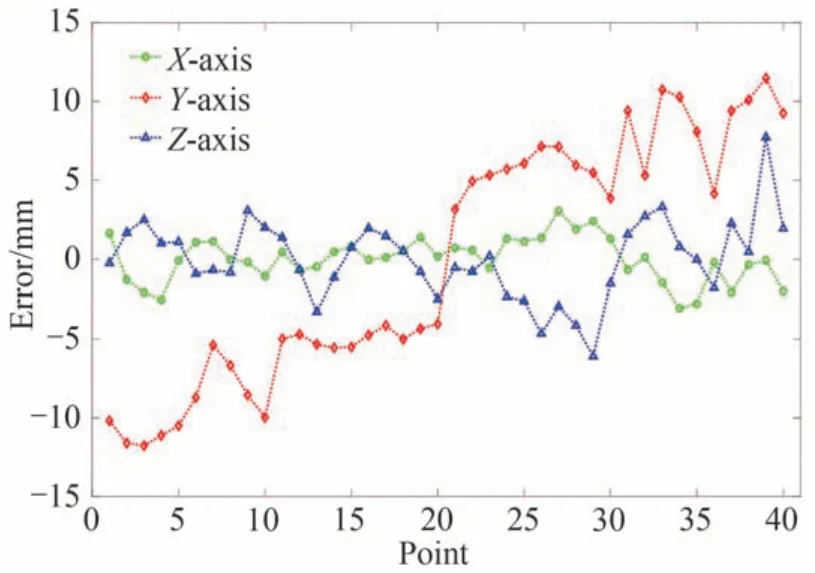
图16 整体区域Vicon 系统定位精度Fig.16 Vicon positioning accuracy in the whole area

从图12～16 中可以看出

1）各分区域下系统在X、Y、Z轴方向的定位精度多数在2 mm 以内，表明各分区域下光学运动捕捉系统的定位精度较高。

2）整体区域下系统在X轴方向和Z轴方向的定位精度多数在5 mm 以内；Y轴方向的定位精度较差，部分点在Y轴方向的误差超过10 mm。结合图6 和图10 分析，原因在于全站仪架站位置位于测试场中心附近，且测试场的长边与全站仪的Y轴近似平行。而整体区域是由沿Y轴方向的四个分区域组成，且靠近测试场中间区域共视相机的数量多，测试场边缘共视相机的数量少。因此，Y轴误差较大且呈现沿测试场中心向边缘逐渐增大的趋势。

3）整体区域下动捕系统的定位精度明显低于各区域下动捕系统的定位精度。原因在于整体区域由四个分区域的相机组成，区域间具有共视区域的相机数量少，相机与目标的距离远，以及场景振动等因素的影响，导致整体区域下光学运动捕捉系统的实际定位精度严重降低。

经过计算得到，四个分区域和整体区域下光学运动捕捉系统的定位均方根误差（Root Mean Square Error，RMSE）如表3 所示。

表3 系统定位精度Table 3 Target position

从表3 中可以看出：

1）区域一、区域二、区域三、区域四的点位RMSE 分别为2.385 mm、0.877 mm、1.787 mm 和2.890 mm。经分析区域一和区域四位于测试场边缘，区域二和区域三靠近测试场中心，因此区域二和区域三可观测到的相机数量多于区域一和区域四，因此定位精度稍优于区域一和区域四。

2）整体区域的点位RMSE 为8.126 mm，相较于各分区域下的定位精度明显降低。原因在于整体区域由四个分区域组成，且相邻分区域的共视相机数量较少，因此，当所有相机组成一个整体的视觉运动捕捉系统时，受相机数量和相机分布等因素的影响，整体区域下光学运动捕捉系统的定位精度明显降低。

实验二是Vicon 光学运动捕捉系统和度量运动捕捉系统的外参标定。由于两个系统之间的相机非共视，因此如何实现系统间的外参标定是面临的难题。基于Vicon 系统精度标定的思路，利用全站仪分别进行Vicon 区域和度量区域下的公共点测量，分别计算Vicon 坐标系到全站仪坐标系的坐标系矩阵和度量坐标系全站仪坐标系的坐标转换矩阵，最后计算度量系统到Vicon 系统的坐标系转换矩阵，实现Vicon 系统和度量系统的外参标定。图17 所示为度量系统的相机分布，Vicon 系统的相机分布如图9 所示，图18 为度量/Vicon系统外参标定实验。

图18 Vicon/度量系统外参标定实验Fig.18 External parameter calibration experiment between Vicon system and NOKOV system

实验过程中，利用全站仪在Vicon 系统的测量区域采集和度量系统的测量区域分别采集10 个公共点和15 个公共点。经过计算，得到Vicon 系统与全站仪坐标系的坐标变换矩阵为

度量系统与全站仪坐标系的坐标变换矩阵为

最终计算得到度量系统到Vicon 系统的坐标系转换矩阵为

由此，度量系统与Vicon 系统的外参标定完成。

5 结论

提出大场景下光学运动捕捉系统的定位精度标定方法。利用同尺寸同心靶球解决全站仪和运动捕捉系统测量点不一致的问题，基于罗德里格矩阵的抗差最小二乘迭代计算坐标系转换矩阵，针对大场景下Vicon 系统的相机空间分布提出分别计算分区域和整体区域下光学运动捕捉系统的定位精度方法。实验结果表明，大场景下光学运动捕捉系统的定位精度明显降低，系统在X轴、Y轴、Z轴和点位精度的RMSE 分别为1.393 mm、7.606 mm、2.496 mm 和8.126 mm。说明大场景下受相机分布、相机数量、场景振动等因素的影响，光学运动捕捉系统的实际定位精度可能严重降低。并利用该方法实现了Vicon 系统和度量系统的外参标定。验证了提出的大场景光学运动捕捉系统精度标定方法的有效性和可行性。随着对光学运动捕捉系统的应用需求和定位精度要求不断提高，提出的方法对未来大场景、复杂场景下光学运动捕捉系统的标定工作具有一定的启发和参考意义。