基于改进多目标粒子群算法的机器人轨迹规划研究

黄婷婷

(上海电子信息职业技术学院中德工程学院,上海 201411)

现代化物流仓储多采用中心化和立体化的管理模式[1]。物流仓储中心占地面积很大、分区较多,给商品管理和取放都带来巨大的困难。物流仓储机器人又被称为自动引导车(automated guided vehicle,AGV)[2],其采用激光引导或视觉引导等方式[3],选择最佳的行进路径运输货物,并通过最优路径的规划、选择提升效率和避免碰撞。文献[4]提出一种基于滤波惯性导航的轨迹规划方法,文献[5]提出一种基于即时定位与地图构建(simultaneous localization and mapping,SLAM)的地图信息融合与匹配算法,文献[6]提出一种基于人工势场的路径规划方法,文献[7]提出一种基于人工神经网络(artificial neural network,ANN)的机器人运动轨迹规划方法。上述算法从不同的视角解决了物流机器人的轨迹优化问题,但在最优路线选择、工作效率和多机器人避碰等方面都存在一定问题。针对现有物流机器人轨迹规划算法存在的不足,本文提出一种基于多目标粒子群算法的机器人轨迹规划方法,并基于二进制优化算法和模拟退火(simulated annealing,SA)算法对经典粒子群算法进行二次性能优化,提升全局寻优的性能,在确保路径轨迹经济的前提下,重点提高机器人的工作效率和实用性。

1 仓储环境建模与物流机器人定位

1.1 仓储环境建模

本文在对机器人轨迹进行规划前,先基于格栅法对仓储环境建模,将仓库环境分为自由格栅(用白色方格表示)和障碍格栅(用黑色方格表示),其中自由格栅表示区域内没有障碍物,机器人能够自由通过,而障碍格栅是机器人在工作中需要躲避或绕行的障碍物,图1为一个24 m×24 m的仓库规划格栅图。

图1 仓库格栅建模示意图

图1中黑色的方格表示存放物品的仓储货架,白色方格为通道,圆点表示货架的信标(每个信标包含唯一的空间位置信息)。每个黑色方格和白色方格均为边长1 m的正方形,机器人在白色方格内可以自由通行,但在工作中要避免与货架发生碰撞。

1.2 物流机器人的空间定位与纠偏

以世界坐标系为基础构建一个观测模型,用于物流机器人的定位,如图2所示。

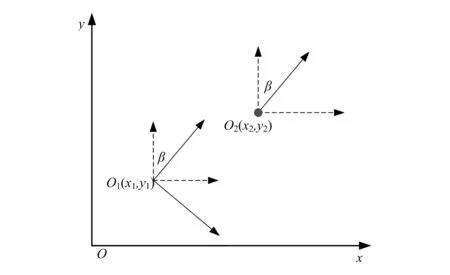
图2 物流机器人的空间定位示意图

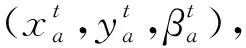
(1)

(2)

对机器人当前位置的精确定位和纠偏是优选行进轨迹的前提,如果不对位置偏差做实时跟踪,当机器人与多个信标进行通信时,就容易造成偏航或对轨迹寻优构成干扰。

2 基于改进多目标粒子群的轨迹规划

2.1 基于多目标粒子群算法的非劣解集筛选

(3)

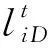
(4)

(5)

图3 多目标粒子群优化过程

由于种群中的多个粒子在目标寻优过程中存在多个局部范围内的最优解,因此本文基于适用的二次寻优规则,构建了一个临时存储非劣解的容器[10],并对整个种群进行二次寻优。基于二进制算法对多目标粒子群算法进行第一次优化,多目标粒子群算法的关键步骤是确定当前粒子的位置和运行速度,二进制优化的原理是采用二进制编码0和1限定粒子在局部和全局的位置,进而提升粒子在局部和全局寻优性能。二进制算法优化下第(t+1)时刻的粒子位置表示为:

(6)

式中:α1和α2为[0,1]之间的随机数,s()为适应度函数。具体表示如下:

(7)

2.2 多目标粒子群算法的二次改进

为进一步提升多目标粒子群算法的全局寻优性能,避免在非劣解集寻优时陷入局部最优解,本文基于SA算法对多目标粒子群算法进行二次优化。模拟退火的基本环节是设定初始温度、选择退温的方式并确定接受劣等解的概率函数P(x) 等。设定种群加温时的初始控制参数ξ0:

ξ0=s(lg)/lnn

(8)

式中:s为多目标粒子群算法的适应度函数,lg为全局最优位置,n为种群的粒子个体数量。引入模拟退火系数ζ作为升温过程中的重要调整参数,通过控制升温和降温的方式调整种群粒子的寻优性能。第(t+1)时刻的温度控制参数ξt+1表示如下:

ζt+1=ξ·ζt

(9)

式中:ζt为第t时刻的温度控制参数。

(10)

(11)

式中:γ为压缩因子。γ计算过程如下:

γ=2τ1τ2/[2-(κ1+κ2)-

(12)

引入模拟退火算法后,能够进一步提升全局优化性能,并最大限度地避免在非劣等解集寻优中再次陷入局部最优解。

3 基于改进粒子群的物流机器人轨迹规划与避碰

3.1 基于改进多目标粒子群的拥塞规划

仍旧基于格栅法建立机器人拥塞概率地图G,其中第j个机器人与其他机器人发生拥塞的概率表示为Pj,很显然发生拥塞的概率Pj与第j个机器人在同一地点停留的时间tstay及该地点周围机器人的数量m相关,即Pj是tstay和m的函数:

Pj=h(tstay,m)

(13)

由于影响Pj的因素较多,包括格栅的设置距离l、机器人的运行速度Vj、角速度ωj和转向角度θj等,因此需要将时间因素和数量因素分解(Pj分解为Ptstay(在同一地点停留的概率)和Ptm(周围存在其他机器人的概率)的乘积),再进行乘积表征以提升影响概率计算的准确性:

(14)

式中:ψ1、tm分别为概率控制参数和时间控制参数。

其中停留时间因素可以基于以下几个参数来表示:

(15)

式中:v为机器人的运行速度,θ为旋转角度,ω为角速度。如果t时刻机器人j所处位置为点O1(x1,y1),其下一目标点的拥塞概率(多机器人同时运动发生拥塞的概率)为PO1。如果当前位置没有发生其他拥塞,只存在基于多目标改进粒子群算法合理控制行进路径的拥塞,就能够有效避免机器人j与其他机器人之间发生拥塞。

3.2 轨迹规划中的避碰及路径冲突消解

不同机器人之间的路径冲突主要分为横向冲突和纵向冲突,通常发生路径冲突时后台控制系统给出的指令是挑选通道独占访问(路径已经确定的机器人具有优先权),其他干扰机器人会进入通道等待进而消解冲突。横向冲突的消解方案如图4所示。

图4中M1和M2分别表示同时作业中的两台物流机器人,由于M1先规划了路径,具有优先权,为了避免物流机器人发生碰撞,M2要通过等待或进入其他路径暂时躲避。图4(a)表示M1沿过道直行且具有优先权,此时M2根据后台系统指令及改进多目标粒子群算法规划的路径以及M1、M2目标位置,选择3种消解方案——原地暂停躲避、左转躲避和右转躲避;图4(b)表示M1右转,此时M2也有3种消解方案,即原地暂停躲避、左转躲避和右转躲避,M2根据总体路径规划选择最经济的行进方案;图4(c)中M1的路径是左转,此时M2为了防止与M1发生碰撞,依据后台系统传递的信息,并且根据改进多目标粒子群算法规划的路径选择左转躲避或右转躲避。

两台机器人纵向行进路径消解和避碰方案如图5所示。

图5 机器人纵向冲突的3种消解方案

由于仓储物流仓库的立体置物架多采用纵向排布方式,还要考虑到仓库边缘区域较为狭窄等因素的综合影响,因此选择了图5所示的物流机器人冲突消解方式。

4 实验

4.1 实验环境设置

选定一个空闲的仓库,并按照图1中的格栅来布置现场,单位格栅大小为1 m×1 m,整个仓库为24 m×24 m的方形场地,货架的布置和通道的宽度等参数与建模示意图一致。在每个货架对应位置布置一个高性能防水信标(C127042,工作主频为2.45 GHz)。测试用的物流机器人为MIR ABB1600型号,机器人的4个侧面都内置了LIDAR型号的高精度通信传感器,用于机器人定位、机器人之间及与信标传感器之间的通信,MIR ABB1600型物流机器人实物如图6所示,机器人相关参数见表1。

表1 MIR ABB1600型机器人的相关参数

图6 测试用MIR物流机器人实物图

实验过程中多目标粒子群算法相关参数见表2。

表2 多目标粒子群算法相关参数

4.2 实验结果与分析

4.2.1轨迹规划效果及机器人运行效率对比分析

在实验仓库区域内随机布置一点Q′,验证本文算法及4种传统算法(文献[4]～文献[7]算法)从起点Q到目标点Q′的路径规划情况,为模拟真实的物流作业情况,在仓库内随机增加了另外2台静止的机器人参与对比,各算法的路径规划情况如图7所示。

图7 各算法到目标点轨迹规划结果对比分析

由图可以看出,在存在障碍物的前提下,本文基于多目标粒子群的路径规划算法所选择的路径为最短路径。各算法规划路径的行进距离对比见表3。

表3 各算法规划路径的行进距离对比 单位:m

从单次随机样本抽样分析结果可知,基于改进多目标粒子群算法的路径规划距离最短,相较于其他算法具有一定优势。改进多目标粒子群算法通过机器人自带传感器与信标、其他静止的机器人进行实时数据交互,能够在全局范围内选择最优的路径。调整目标点Q′位置,以增加随机采样样本数量的方式,观测在多个样本环境下多目标粒子群路径规划算法的稳定性。本文选择的目标位置样本数量为10,测算结果见表4。

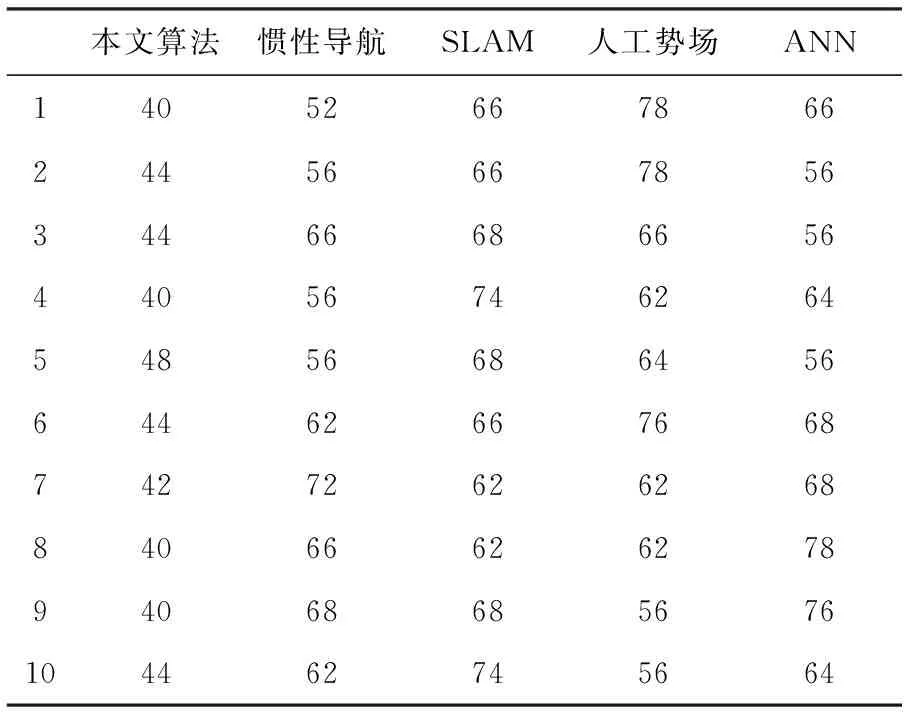
表4 多样本下各算法规划路径行进距离对比 单位:m

由表可知,在多样本环境下,本文基于改进多目标粒子群算法所规划的路径距离最短,并且能在全局范围内筛选最优的行进路径。与多个样本点路线距离均值对应的时间均值统计如图8所示。

图8 时间均值对比分析

由图可知,本文算法的物流机器人路径寻优耗时少于40 s,效率较高,远优于4种传统路径规划算法。物流机器人运动效率除了与距目标的距离相关以外,还与躲避障碍物(其他机器人)的能力关系密切。本文算法能够充分利用固定的信标数据和其他机器人的定位信息,实现在全局范围内的路径选择,提升了机器人的工作效率。

4.2.2多个机器人避障结果测试与分析

20个随机目标样本的时间均值对比如图9所示。

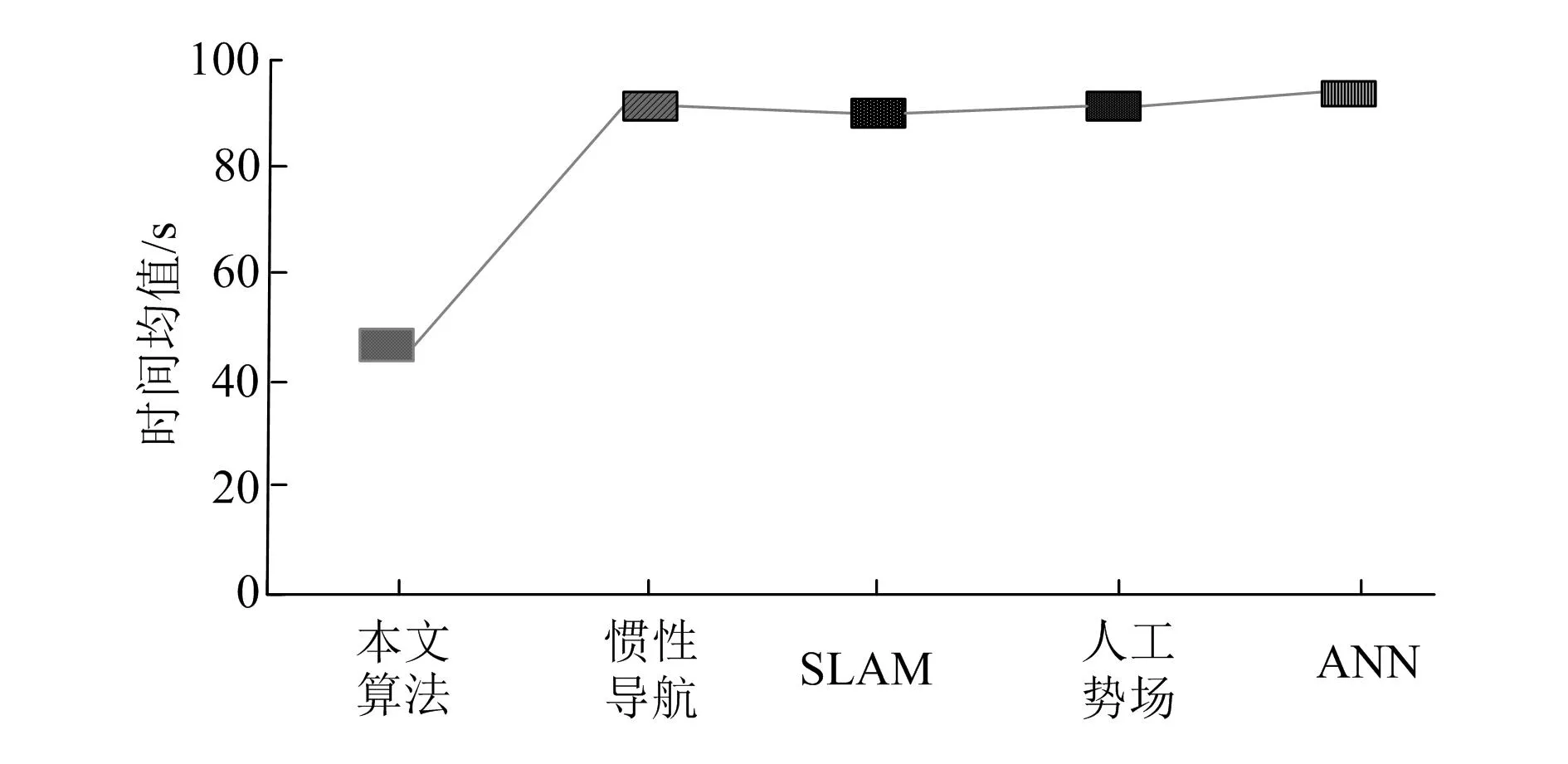
图9 机器人移动条件下时间均值对比分析

与距离增加类似,机器人移动条件下时间均值也有所增加,但基于效率视角分析,本文算法效率要更高,碰撞次数的统计见表5。

表5 各算法下机器人发生碰撞的次数

由表可知,在本文算法下,物流机器人之间并没有发生碰撞情况,而在其他规划算法下,均出现了少量的机器人碰撞事故。

5 结束语

本文设计了一种基于改进多目标粒子群的物流机器人轨迹规划算法,引入非劣解存储器改善局部寻优能力,利用SA算法对经典粒子群算法进行二次优化,提升了改进算法的全局寻优能力,并重点消解了多个物流机器人同时作业时出现的拥塞问题和碰撞风险。实验结果显示,在改进多目标粒子群优化算法的路径规划算法控制下,无论其他机器人处于静止还是移动状态,目标机器人都能筛选出全局范围内的最优路径,有效避免了碰撞事故的发生。