基于数据融合的高速电气化铁路牵引供电安全智能监测方法

于士伟

(中铁建大桥工程局集团电气化工程有限公司,天津 300300)

牵引供电系统能否正常工作,对列车的安全运行有很大的影响。由于目前的高速铁路密度大、交通量大,一旦发生故障,将会引发连锁效应,导致多条线路发生故障,从而造成重大的经济损失。与传统电力系统相比,牵引供电系统具有多样的形式和复杂的结构。列车负载处于流动状态,在运行过程中会受到接触网的开放性、滑动性等因素的影响。这些因素增加了牵引供电系统的复杂性,也增加了事故发生的风险。因此,牵引供电系统的设计、建设及维护需要高度关注安全性和可靠性,以确保列车的安全运行。为确保电力系统安全、可靠地工作,必须在发生故障时及时、准确地对故障产生的原因进行分析,以减少停电面积,快速恢复电力供应。

随着电气化铁道的发展,牵引变电站的数量不断增加,且电力监控系统的集成化和自动化水平也在不断提高,一旦牵引供电系统出现故障,将会产生大量的报警和监控数据,工作人员需要适应和利用现代化的信息处理和分析工具,以便更高效地处理和解决故障,进一步提升电力安全智能监测系统的效能。文献[1]提出了一体化铁路管型母线智能监测预警方法,在管型母线出现问题时准确发出预警信息。但是该方法进行监测时所花费的时间较长,并且监测效果较差。

数据融合技术是一种信息处理技术,它通过计算机对已有的多个观测资料进行实时分析和综合处理[2]。本文针对电力系统监控数据量大的特点,提出基于数据融合的高速电气化铁路牵引供电安全智能监测方法,以期解决目前电力系统监控效率较低的问题。

1 高速电气化铁路牵引供电安全智能监测方法设计

引起电气化铁路牵引供电系统故障的主要原因可以分为两个方面:一是该系统自身的可靠性问题,二是自然环境、自然灾害等外在条件的改变[3-4]。系统的内部要素是可以控制的,应该在系统的设计中加以解决,即在系统设计时,通过优化设计方案来满足特定的项目需求,提高设计质量,包括改善设备的选用、质量控制和设计方法等。这些措施旨在确保系统的安全可靠性,并提高其性能和效率。而外在因素是指无法预测或直接控制的因素,这些因素可能对系统的运行产生影响。尽管目前无法完全控制这些外部因素,但可以通过合理的系统设计和决策来减轻其影响,并采取适当的风险管理策略[5-6]。

1.1 高速电气化铁路牵引供电安全智能监测数据压缩

在安全智能监测过程中,由于数据较多,因此需对数据进行压缩。数据压缩主要是指在不丢失有用信息的前提下,按照一定算法对数据重新组织、去除冗余信息的一种方法。假设采集到的高速电气化铁路牵引供电安全监测的信息源由Q个事件组成,每个事件出现的概率均为q(ai),则将概率空间表示为:

(1)

式中:X表示概率空间中的一个事件集合,q(X)表示事件集合X的概率,ap表示一个特定的事件。

假设事件ai已经发生,则将该事件含有的信息量记作自信息,将其定义为:

(2)

式中:I(ai)表示事件的自信息。

将自信息的数学期望值称为信息源的熵,表示事件概率分布条件,记作:

(3)

式中:H(q)表示信息源的熵,H(q1,q2,…,qq)表示联合概率分布q1,q2,…,qq下的联合熵。

当信号源呈等概率分布时信息熵会达到最大值,将其记作:

(4)

信息源的冗余度R可以通过熵来计算:

R=Hmax(X)-H(X)=log2q-

(5)

式中:H(X)表示事件集合X的熵,Hmax(X)表示事件集合X熵的最大值,g表示X的概率分布。

通过上述计算,可对原始监测数据进行建模和量化处理,从而更有效地实现数据的压缩。

1.2 高速电气化铁路牵引供电安全智能监测指标分析

在安全智能监测过程中,根据设备当前的运行情况进行状态分类,并建立相应的监测指标,计算监测指标的可靠度[7]。设备状态分类如图1所示。

图1 设备状态分类

以电力系统的单机可靠性评估为例,对带电作业情况、调度停运设备、计划停运、检修停运、分计划停运等5项指标进行监测。

运行系数AF是电力系统单机可靠性评估中的一个重要指标[8-9],AF的计算公式为:

(6)

式中:AH为电力系统的可用时长,PH为电力系统的故障停运时长。

可靠性SF是一个用于评估系统或组件在规定时间内正常运行能力的指标,SF计算公式为:

(7)

式中:SH为统计时间内系统处于正常工作状态的时长,rH为统计时间。

计划停运系数POF计算公式为:

(8)

式中:POH为计划停运的时长。

由公式(7)和(8)可以计算出在统计时间内设备处于停机状态的可能性(即停机概率)[10]。计划停运率POR计算公式为:

(9)

式中:POT为计划停运次数,Z为统计时间内参与计划性停运的设备数量,M为统计时间内设备的总运行次数。

暴露率EXR计算公式为:

(10)

在电力系统监测过程中,接触线张力是重要的监测参数之一,用于评估牵引供电的安全状态。接触线张力是指供电系统中接触线所受到的张力大小,其变化会直接引起其他动态参数变化,从而影响安全监测结果,因此要对其进行监测[11]。柔性悬挂系统是指能够在多个方向上具有较大位移或变形能力的系统。柔性悬挂系统对于减震、吸收冲击和提供舒适性具有较好的效果。本文主要针对柔性悬挂系统进行分析[12]。由于接触线是柔性的,当受到外力影响时,其会发生形变,进而引起接触线末端张力的变化。这种形变和张力变化可能会导致接触线明显振动,为此需要计算动态抬升量y:

(11)

式中:ρ为接触线的密度参数,C、v分别为振动波的传播速度和运行速度,l为线索长度,d为基础压力,t为接触时间[13]。

传播速度C计算公式为:

(12)

式中:ζi为第i阶振动波形的阻尼比,T为接触线张力,E为弹性模量,I为接触线的截面惯性矩。使用上述指标可反映设备的实际运行状况[14-15]。

1.3 基于数据融合的牵引供电安全智能监测

为了提高监测结果的稳定性,采用D-S证据推理的数据融合方法对数据进行融合处理,融合过程如图2所示。

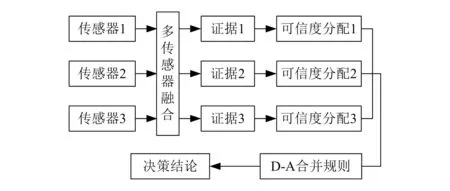
图2 数据融合过程

将识别框架记作Θ,Θ={θ1,θ2,…,θn},θn代表识别框架中的一个特定识别框。一个识别框表示一个样本区域,包含位置和边界信息。基于基本概率赋值函数m的计算规则可以获得关于不同假设或事件的置信度和可信度度量。这些度量可用于进行识别和分类任务,有利于根据可信程度进行推理并得出准确的识别结果。识别公式为:

(13)

式中:m(A)为命题A的基本概率分配函数。

由于有多个信任函数,因此建立分配框架,公式如下:

(14)

式中:Ak为第k个信任函数对应的基本概率分配函数,mk为融合后的基本概率分配函数。

由此实现了监测数据的融合,完成了基于数据融合的高速电气化铁路牵引供电安全智能监测。

2 实例分析

为验证本文提出的基于数据融合的牵引供电安全智能监测方法的有效性,进行实例分析。

2.1 实验对象

实验主要分为两部分:第一部分,对历史数据监测,将2015年京沪高速铁路区段作为实验对象,主要分析故障供电牵引网不可用时长、平均连续可用时长;第二部分,对京沪高速铁路进行在线监测,主要验证高速电气化铁路牵引供电安全在线监测时长和精度。

2.2 故障供电牵引网不可用时长分析

采用本文方法和文献[1]方法对相关信息统计与分析,监测出该牵引网内不可用的时长,对比结果见表1。

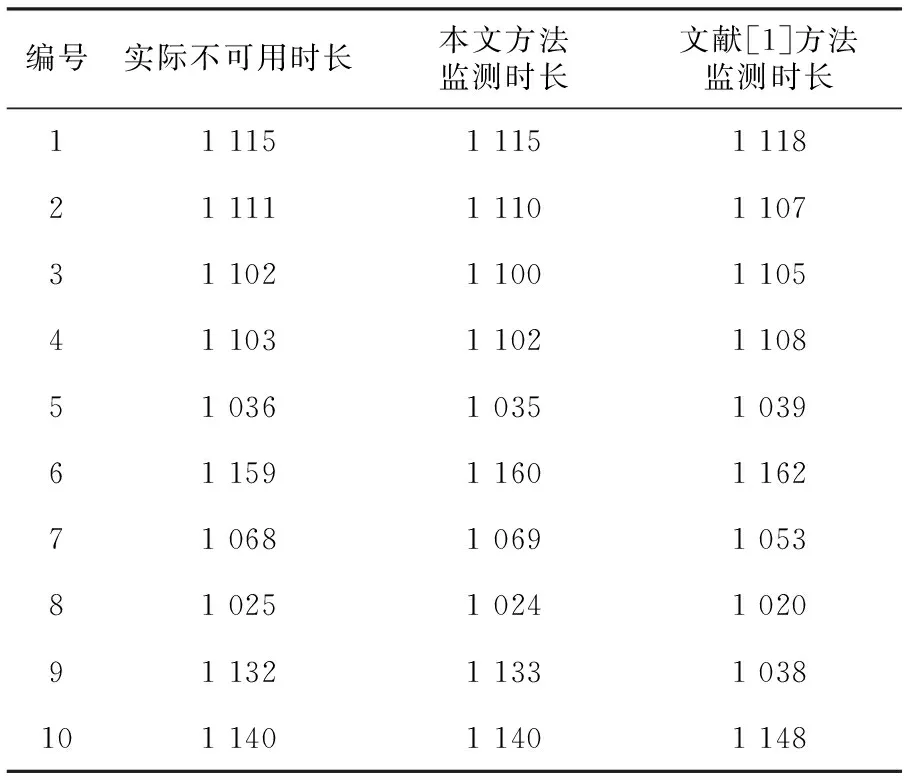
表1 故障供电牵引网不可用时长分析 单位:min

由表可知,本文方法监测时长与实际不可用时长最大相差约2 min,差距较小,说明本文方法能够较为准确地监测牵引网的不可用时长,而文献[1]方法监测的不可用时长与实际不可用时长相差较大。

2.3 平均连续可用时长分析

将本文方法和文献[1]方法监测到的平均连续可用时长与实际平均连续可用时长对比,结果见表2。

表2 平均连续可用时长分析 单位:min

由表可知,本文方法获得的时长与实际值相差较小,文献[1]方法获得的时长与实际值相差较大,由此验证了本文方法的有效性。

2.4 监测时间分析

采用本文方法和文献[1]方法,对高速电气化铁路牵引供电安全在线监测所用的时间进行对比分析,结果如图3所示。

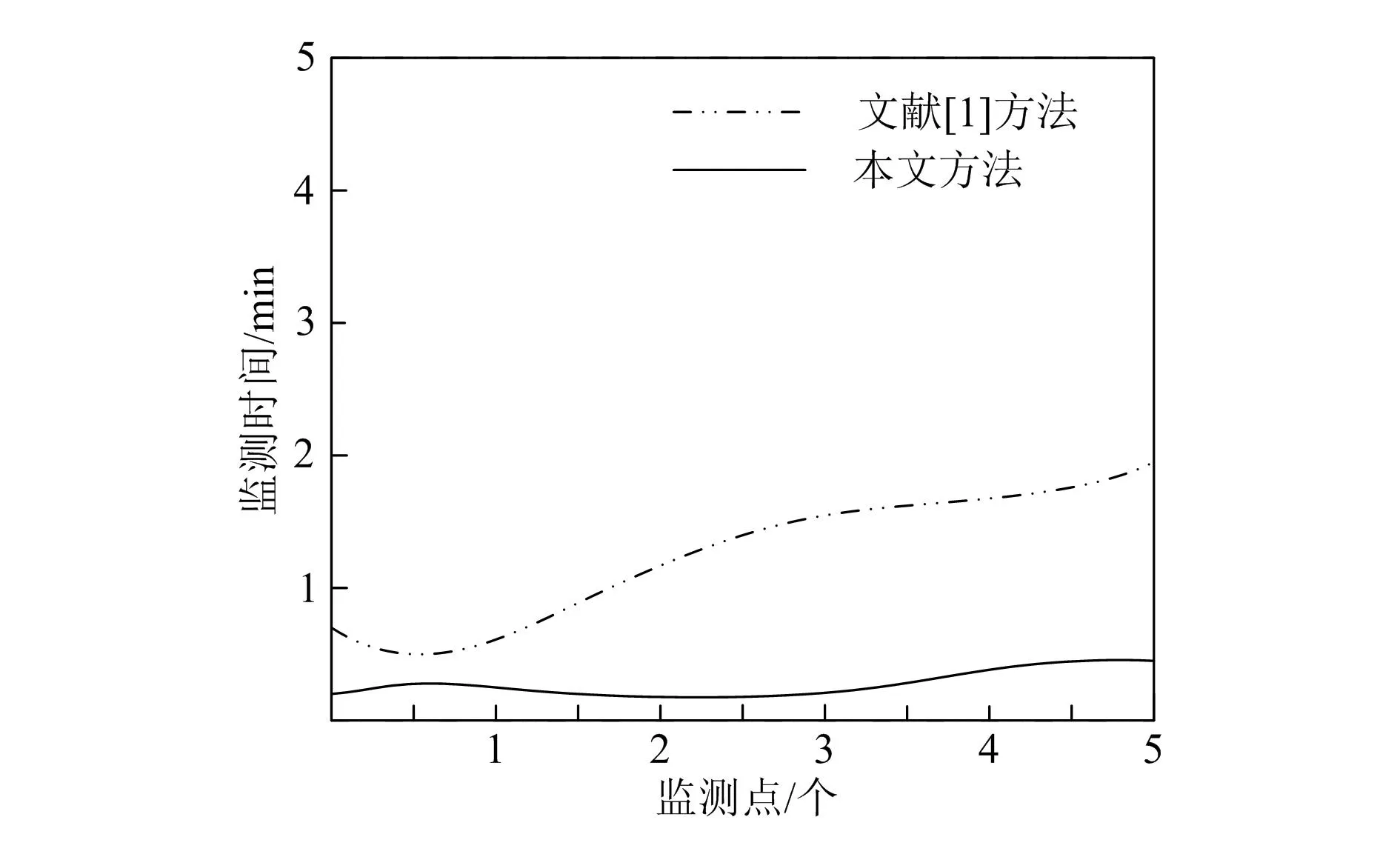
图3 监测时间对比

由图可知,本文方法监测所用的时间明显少于文献[1]方法监测所用的时间,具有一定的实用性。

2.5 监测精度分析

采用本文方法和文献[1]方法,对高速电气化铁路牵引供电安全在线监测精度进行对比分析,结果见表3。

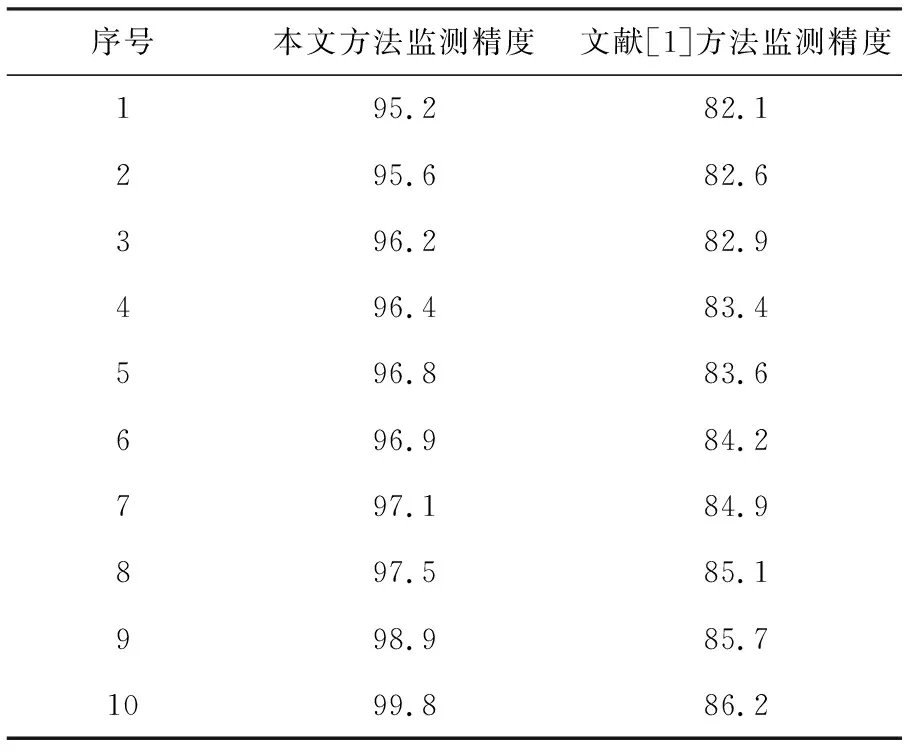
表3 两种方法的监测精度对比结果 %

由表可知,本文方法监测精度最高可达99.8%,而文献[1]方法最高只有86.2%,证明本文方法监测效果较好。

为进一步验证本文方法的精度,采用本文方法和文献[1]方法对接触网电压值进行监测,并将监测结果与实际值进行电压误差对比,结果如图4所示。

图4 接触网电压值误差对比结果

由图可知,本文方法监测到的电压值波形与实际输出的波形基本一致,在03:00时出现一次波动,虽然波动较小,但仍然能准确监测出接触网的电压值,准确性较高,而文献[1]方法监测到的电压值波形与实际输出的波形相差较大,说明本文方法的监测精度较高。

3 结束语

本文提出了一种基于数据融合的高速电气铁路牵引供电安全智能监测方法,实验结果表明,该方法具有较高的监测准确性以及监测效率。通过建立监测指标,反映设备的实际运行状况;通过数据压缩算法,对采集的数据进行了压缩处理,并去除冗余数据,有效提高了后续数据处理的速度。然而,在实际的高速电气铁路牵引供电安全监测过程中,监测效果还可能受到其他因素的影响,所以在后续研究中,还需要重点研究影响因素,以进一步提高牵引供电安全智能监测效果。