障碍物环境下机械臂避障轨迹检测研究
别红玲,周 波
(1.上海城建职业学院人工智能应用学院,上海 201415) (2.浙江交通职业技术学院海运学院,浙江 杭州 311112)
随着机器人技术的不断发展和应用,机器人在工业生产、服务领域等方面有着广泛的应用前景[1]。作为机器人的组成部分[2],机械臂在操作过程中经常会面临障碍物的干扰,这给其在复杂环境下的运动与避障带来了挑战[3-4]。
许多学者对机械臂避障路径规划进行了研究,如杨英浩等[5]通过运动学分析了机械臂的运动且对快速扩展随机树(randomized rapidly-exploring tree,RRT)算法进行了改进,利用B样条曲线拟合以及能量最小逆解法优化路径,实现了最佳的避障路径规划;朱战霞等[6]对障碍物以及机械臂运用包围盒以及空间叠加思想进行了简单描述,将机械臂视为多个直线段,障碍物视为球体,根据二者相对位置检测是否碰撞,将机械臂的关节参数进行参数化,通过粒子群算法得出最佳的机械臂避障路径;熊志金等[7]利用动力学模型对机械臂关节运动添加了约束,应用RBF神经网络减少逼近控制器的误差,并减少机械臂冗余动作,使机械臂获得最佳的避障路径。上述方法虽然能够完成机器人机械臂的避障路径规划,但是也存在着一些不足,如对障碍物进行简化建模虽然可以节省空间,但简化建模的障碍物体积过大,导致模型中存在大量机械臂能够移动的空间,进而使模型不够精确;规划的路径并非最优路径;路径规划失误的比例较大等。
本文采用C-空间建模方法设计障碍物环境下机械臂的避障轨迹检测方法。首先对机械臂进行建模,并对障碍物进行简化建模,将建立的模型映射至C-空间中,然后在C-空间内采用改进的A*算法进行路径规划,得出最佳的避障轨迹。
1 机械臂避障轨迹
1.1 机械臂运动学建模
笛卡尔空间是一个三维空间,其中坐标系的3个坐标轴分别对应x、y和z方向。机械臂在笛卡尔空间中的位置和姿态可以通过其关节角度和旋转角度来描述。在D-H参数法中,使用这些参数来描述机械臂不同关节间的相对运动关系[8-9],并计算出不同关节间的运动矩阵[10]。以某机械臂为例[11],根据D-H参数法建立的运动学模型如图1所示,其中(xi,yi,zi)为机械臂关节点Oi的三维坐标。根据机械臂运动学模型得到机械臂的D-H参数,见表1。

表1 机器人机械臂D-H参数
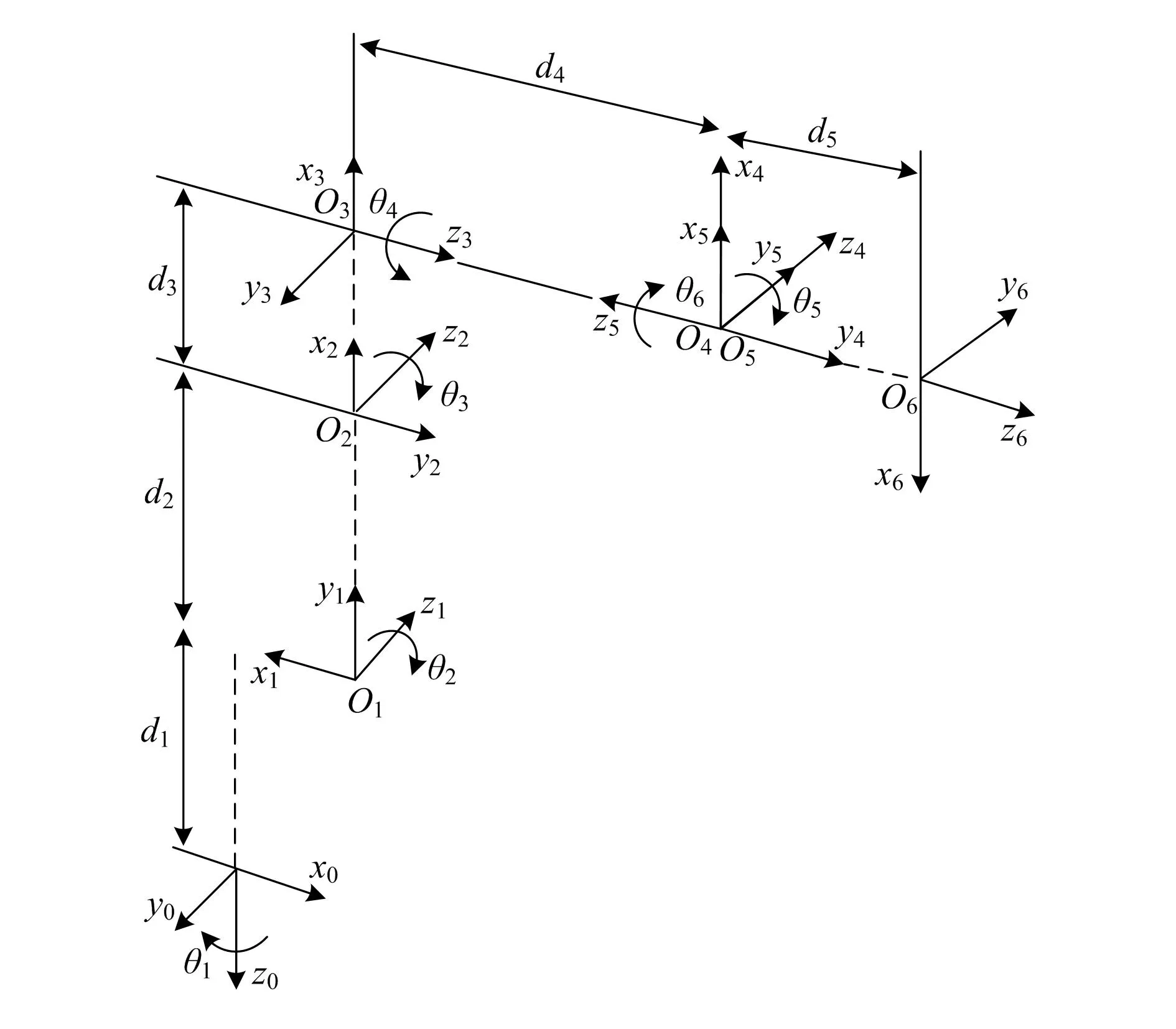
图1 机械臂运动学模型
(1)
式中:c表示cos,s表示sin。
1.2 障碍物简化建模
机械臂夹持器在O4位置,该点的位置向量(px,py,pz)用公式表达为:
(2)
式中:a1、a2、a3为相对位置。
由式(2)可以看出,机械臂夹持器的位置O4由θ2和θ3确定,且机械臂夹角θ2与位置向量px、py和pz没有关系。基于此,可以将以z轴为中心旋转形成的立体图形近似为障碍物。如图2所示,使该障碍物在平面内的投影位于扇形环内,且该扇形的圆心位于坐标系原点,圆心到扇形环内边缘最短距离为rmin,圆心到扇形环外边缘最长距离为rmax。障碍物在该坐标系yOz、xOz平面内的投影与z轴的最大距离为zmax,其与在xOy平面内的投影距离为h。若存在某一障碍物,将该障碍物近似为一个三维扇环,则图2中截面ABCD的数学模型为:
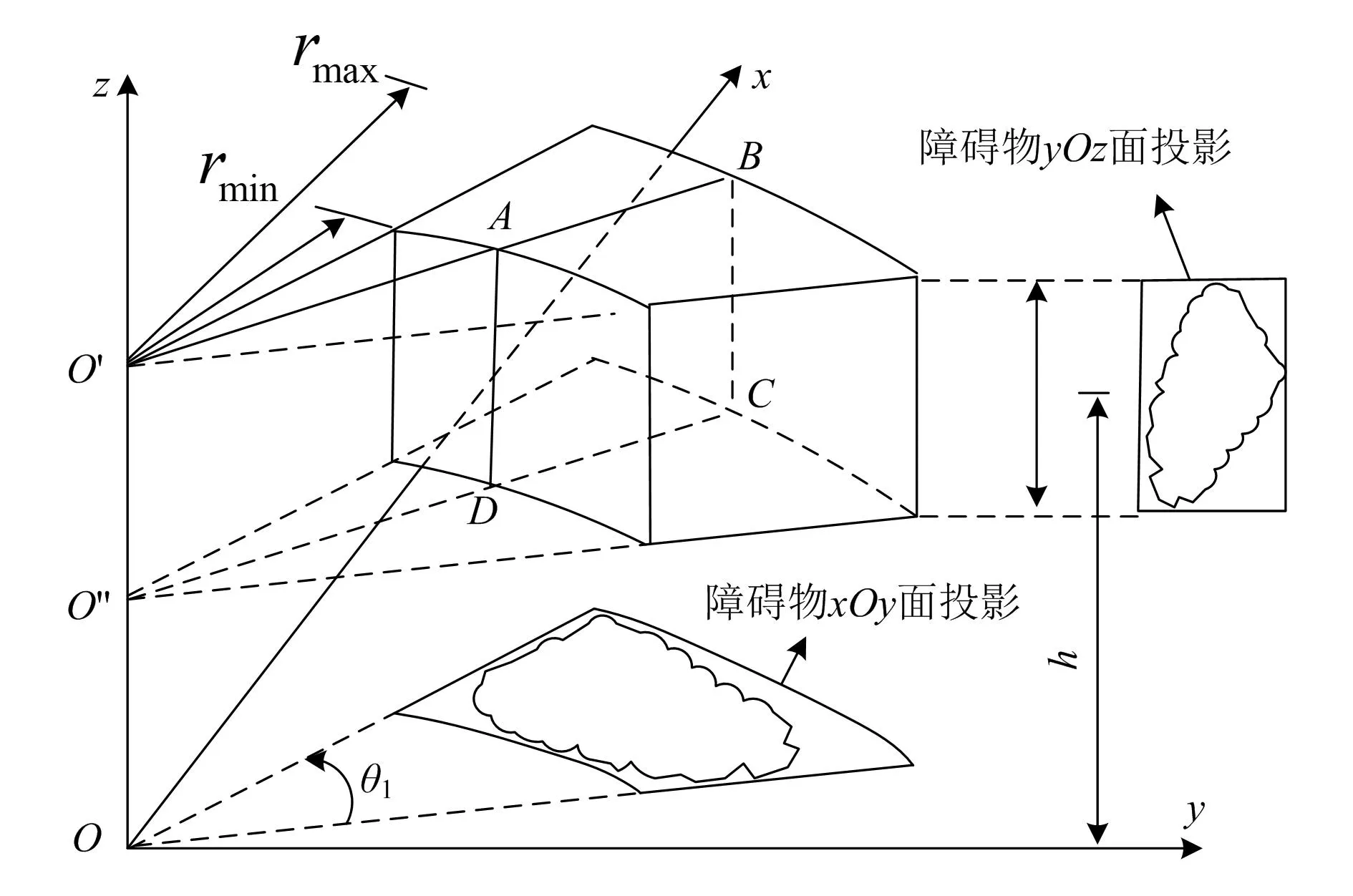
图2 障碍物建模示意图
(3)

若将该障碍物近似为轴截面为圆的三维扇环,则该障碍物的数学模型为:
(4)
(5)
式中:r*为该障碍物近似的截面圆的半径。将两个模型进行组合,可以描述更加复杂的障碍物。
采用上述方法,虽然增加了障碍物建模量,但简化了问题,只需考虑θ2、θ3的变化便可以完成避障路径规划。
1.3 C-空间计算
机械臂的路径规划在考虑夹持器避障的同时也需要考虑其手臂的避障。将机械臂的关节轴视为坐标系,进行C-空间的建立[12],并将障碍物映射到C-空间中,C-空间中障碍补集便是机械臂的运动空间。由于只需考虑θ2、θ3的变化,因此问题便成了对2D-RR的机械臂避障路径规划[13],只需要计算θ2、θ3,躲避C-空间障碍物即可。杆(O2,O3)、杆(O3,O4)和θ2、θ3的方向如图3所示。
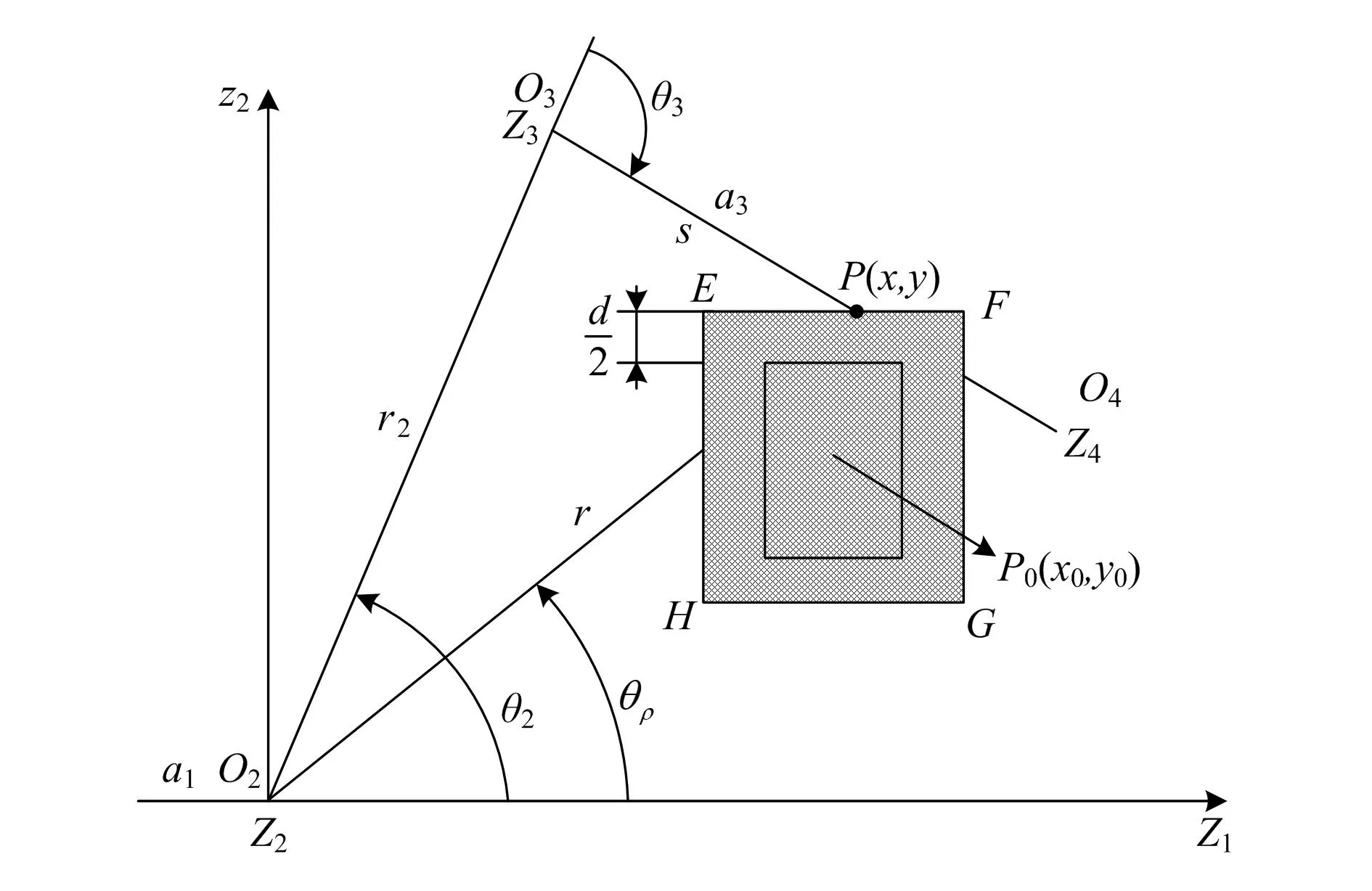
图3 R-R机械臂C-空间障碍计算
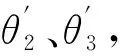
(6)
(7)
式中:θρ=arctan(x/z),r2为杆(O2,O3)的长度。
通过式(6)、(7)便可以计算出机械臂的活动空间,降低算法复杂程度。
1.4 基于改进A*算法的机械臂避障轨迹
在计算出C-空间障碍物的位置以及机械臂可活动的空间后,便可以进行避障路径规划,实现机械臂避障轨迹检测。
1.4.1改进A*算法的避障路径规划
返回出发点或规避障碍物前行是行进中遇到障碍时所给出的两种决策。规划一条两点间的最优路径是A*算法的作用。但在未改进的A*算法中,分别采用统一成本搜索和贪婪搜索算法并不是一种最佳方法[14],因此将统一成本搜索和贪婪搜索算法相结合,借助二者优点实现路径规划。改进后的A*算法不但减少了对存储空间的要求,而且与未改进前相比增加了路径计算的深度,提高了计算速度。在本文中对A*算法进行了改进,机械臂优先对目标点的位置进行象限判断,确定其所在象限后跳过对其他象限的搜索,直接向目标前进,同时在到达目标位置前持续迭代计算。由于排除了其他3个象限,因此能够大幅度减少路径规划的时间,找到最佳路径。
通过如下方法确定机械臂所在象限。机械臂的初始坐标为(Mx,My,Mz),设定目标点坐标为(Tx,Ty,Tz),通过对二者坐标作差Dx=Tx-Mx,Dy=Ty-My,Dz=Tz-Mz,可以确定目标点位于机械臂的某象限内。机械臂需要确定目标点与起始点在三维空间内的相对位置,根据Dx,Dy,Dz的大小,机械臂可以判断目标点相对于起始点的位置。当Dx=0,Dy=0,Dz>0时,机械臂仅需要沿z轴正方向运动,反之,Dx=0,Dy=0,Dz<0时则向反方向运动。以此类推,当Dx=0,Dy≠0,Dz=0时,机械臂沿y轴方向移动;当Dx≠0,Dy=0,Dz=0时,机械臂沿x轴方向移动。最终,当Dx=0,Dy=0,Dz=0时,机械臂便到达了目标位置。
机械臂在第l次由一个位置运动到下一个位置时需要计算成本函数f(l):
f(l)=g(l)+h(l)+p(l)
(8)
式中:g(l)为机械臂由当前位置移动到下一位置时消耗的成本,h(l)为启发式成本,p(l)为机械臂由当前位置移动至下一位置转弯成本。
启发成本为从当前位置移动到停止位置时距离目标点位置的欧几里得距离,即启发函数,此即为A*算法的目标函数,计算公式如下:
(9)
式中:(x1,y1)为当前状态节点的位置,(x2,y2)为目标状态节点的位置。
在取得全部路径点后采用贝塞尔曲线对路径点进行平滑优化,贝塞尔n阶曲线公式如下:
(10)
(11)
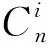
B(t)=(1-t)2P0+2t(1-t)P1+t2P2,t∈[0,1]
(12)
通过式(12)的二阶贝塞尔曲线对A*算法完成路径规划后得到的多个点坐标进行连接,便可得到一条平滑的路径。
1.4.2改进A*算法的机械臂避障轨迹检测实现步骤
1)建立搜索图G,以初始位置节点S为基础,在OPEN表中添加初始位置节点S,令OPEN=f(S),CLOSED=(),其中CLOSED为空,f(S)=0+h(S),其中h(S)为初始化节点S到当前节点的代价值。
2)进行循环判断OPEN表是否为空,若该表为空,则表明无法寻找到目标,结束路径规划;若表不为空,进行路径规划直至到达目标位置。
3)选择f值最小的一个节点进行标记,若该节点未在OPEN表中返回第一步,且该节点存在,则把OPEN表中该值删除,存入CLOSED表。
4)若最佳节点为目标点,表明路径规划成功,算法结束,检测初始节点到目标点间的全部节点,形成最佳路径。
5)假如最佳节点m并非目标点,将最佳节点m进行扩展。扩展后的点形成点集M=(m),在该节点集中的节点不包含初始节点的子节点。该节点集中的节点为最佳节点m的子节点。
6)对M进行判断,若节点m不在OPEN表和CLOSED表中,将其添加到OPEN表中。
7)若在OPEN表中存在重复的节点w和k,而且两节点存在g(w) 8)查看CLOSED表是否重复。 9)将OPEN表中节点根据f值由小到大排序。 10)返回第2)步进行循环,直至获得最佳的机械臂避障轨迹规划结果,将最终输出的避障路径作为对避障轨迹的检测结果。 改进A*算法流程如图4所示。以公式(8)的成本函数f(l)作为目标函数,以1.4节运算过程的参数为变量,评估当前状态到目标状态的代价。 图4 改进A*算法流程 为验证本文方法的应用效果,以某6自由度采摘型机械臂为实验对象,其臂展长为13 700 mm、质量为130 kg、重复精度为0.08 mm、最大负载为6 kg。在实验室内模拟该机械臂应用本文方法后的避障轨迹检测效果。 设置一个模拟的果园环境,包括植物、树木、地形等元素,为了便于实验,将其用矩形、圆形、扇形、梯形和不规则形状替代,以测试机械臂的避障能力。采用S2L激光雷达传感器感知和检测机械臂周围的障碍物。传感器的具体参数为:测量半径0.05~18.00 m,采样频率32 kHz,扫描频率10 Hz,角度分辨率0.12°。设置地图网格分辨率为0.01,启发式函数权重参数为0.25,障碍物网格的代价为0.3,网格连接性为四邻域,运动代价为0.24。 为验证本文方法使障碍物映射到C-空间的结果,对某障碍物利用本文方法进行计算,得出障碍物映射到C-空间的结果如图5所示。由图5可以看出,实际障碍物映射到C-空间后在(0,0)位置呈现旋转对称状态,这是由于R-R机械臂沿y轴运动时根据障碍物的位置进行了一定角度的旋转所造成的。y=1 000表示在C-空间中机械臂的y坐标为1 000。 图5 障碍物C-空间映射结果(y=1 000) 改变y轴与障碍物的位置,障碍物在C-空间映射的结果如图6所示。由图6可以看出,随着障碍物与坐标原点的距离越来越小,在C-空间映射的障碍范围则越来越大,机械臂能够活动的空间则越来越小,这与实际情况一致。 图6 障碍物C-空间映射结果 在机械臂抓取范围内设置矩形、圆形两种障碍物,并设定机械臂目标点,进行机械臂避障测试。设定障碍物位置及机械臂初始位置和目标位置,机械臂避障移动中,关节角度变化如图7所示。由图7可以看出,机械臂从初始位置移动到目标位置过程中,检测到θ2、θ3两个角度经过了多次微小的角度变化,可以看出,本文方法能够有效实现机械臂避障轨迹检测。 图7 机械臂关节角度变化 为验证本文方法实际应用效果,多次更换障碍物并改变障碍物位置,统计机械臂是否能顺利到达目标位置,结果见表2。由表2可以看出,运用本文方法进行避障轨迹检测能够顺利地完成机械臂的避障,虽然在第五次试验中,机械臂手臂与障碍物有接触,但是并未对机械臂造成任何伤害,二者接触后机械臂便立刻停止了运动。 表2 不同情况下机械臂避障效果 为验证本文方法的避障效率,运用文献[5]~[7]方法分别进行了100次3种障碍物的避障测试,与本文方法测试结果进行对比,结果如图8所示。由图8可以看出,避障路径规划开始20次时文献[7]方法路径规划的成功率高于文献[5]和文献[6]方法,但随着实验次数的增加,文献[7]方法避障路径的规划成功率反而逐渐降低,文献[5]和文献[6]方法的路径规划成功率逐渐上升,到实验结束时,文献[6]方法的路径规划成功率高于其余两种方法。而本文方法在实验全过程中路径规划成功率均高于其他3种方法,虽然路径规划的成功率有一定的波动,但一直大于98%。 图8 不同方法的避障结果 通过实验可以看出,采用C-空间进行障碍物映射可以真实地反映障碍物的形状,即距离越近障碍物越大。使用改进后的A*算法能够更加准确地进行路径规划,在存在多种类型障碍物无阻挡的情况下机械臂也能顺利到达目标位置。在确定起始位置和目标位置后,能够准确获得机械臂的移动角度测量结果。
2 仿真实验
2.1 实验准备
2.2 机械臂C-空间映射验证
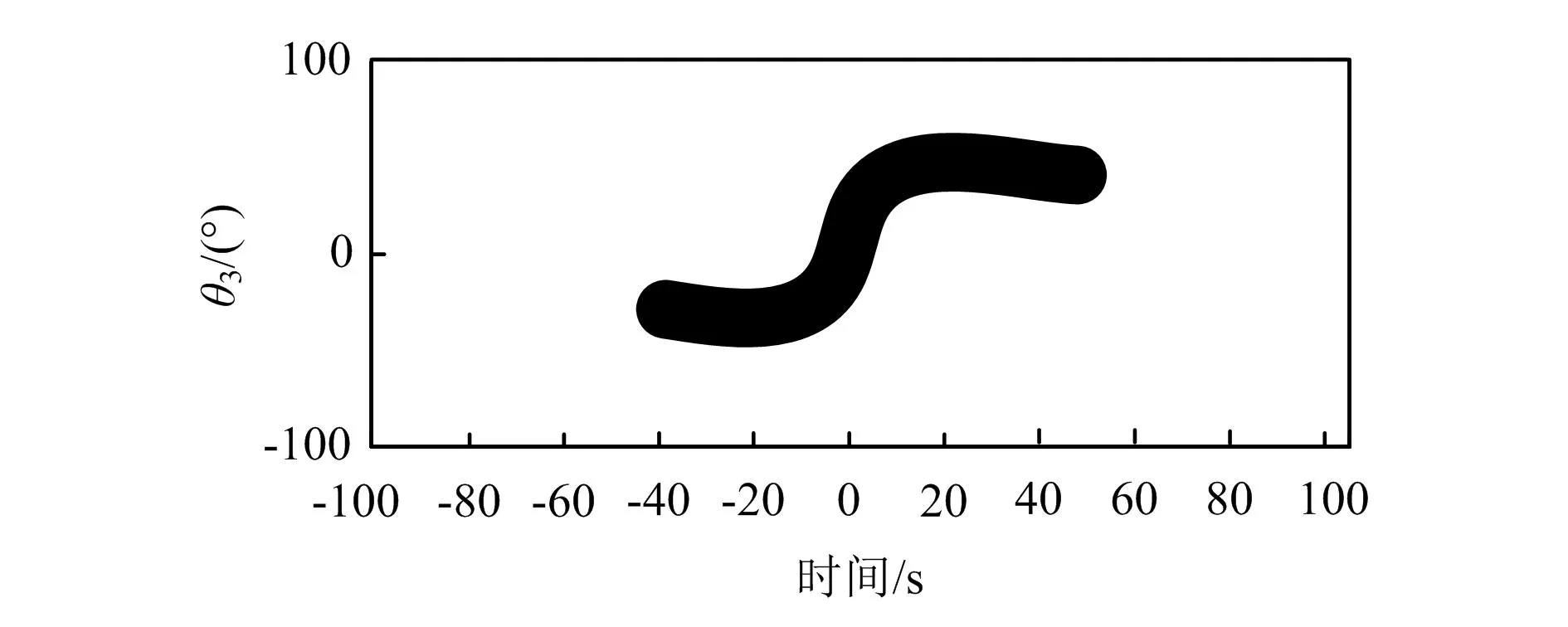

2.3 轨迹检测
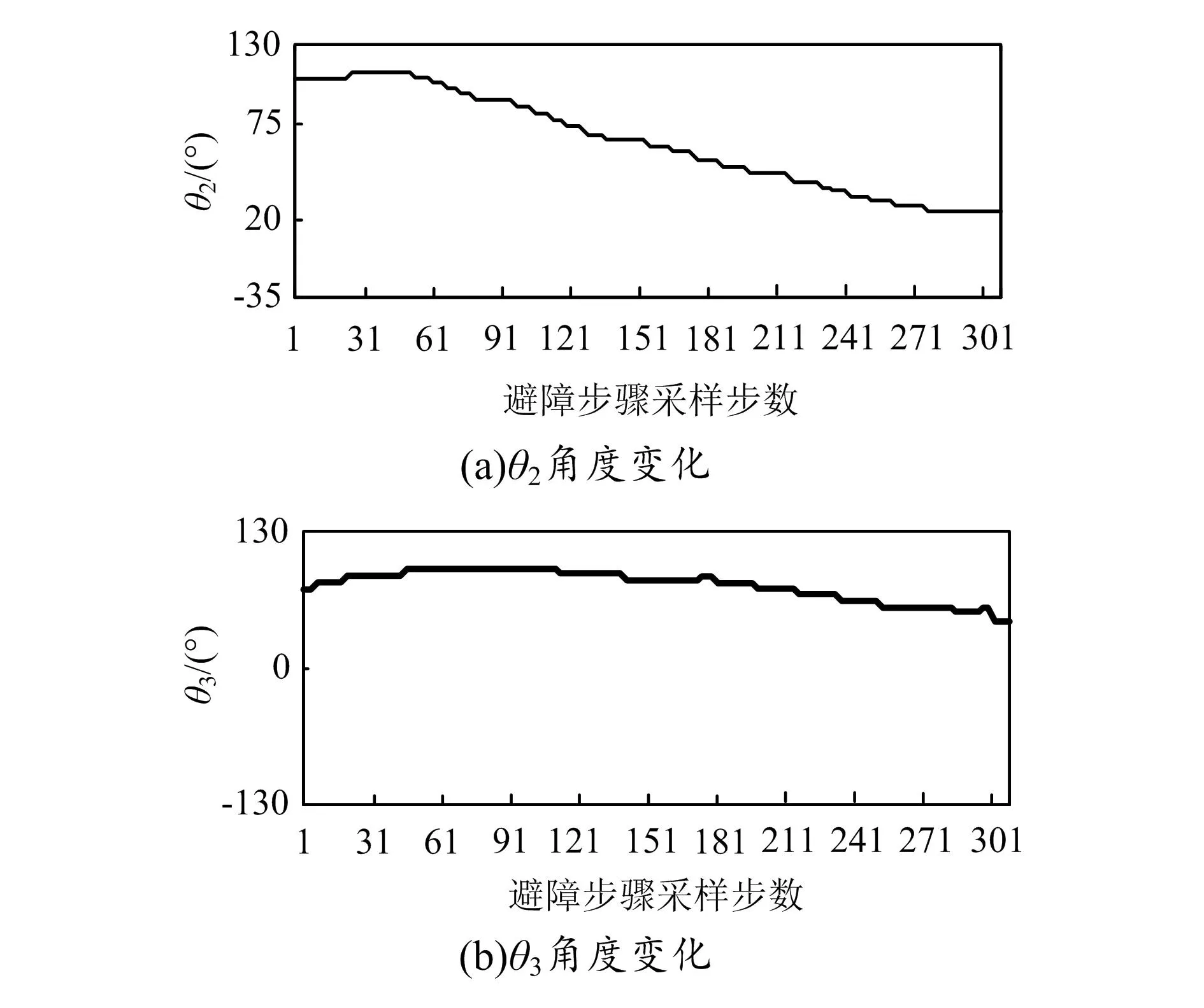
2.4 避障效果

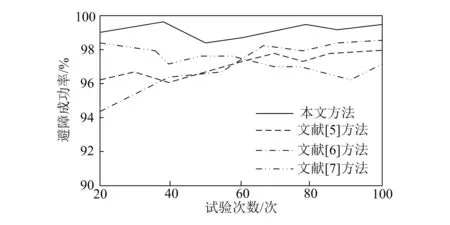
2.5 避障效率
3 结束语

