核心素养导向下的高中数学大单元作业设计*

吴湘芸

⦿ 江苏省宜兴市丁蜀高级中学

崔成林教授认为:作业要关注课堂教学无法达成的需要,作业目标要倡导素养立意,其终极指向高阶目标,即问题解决与应用、思维迁移与创造.单元作业设计是围绕某个单元主题设计的系列作业,使学生结合生活实际,围绕某个数学主题开展深层探究学习,在实践中促进多元化发展.

1 作业设计理念

作业设计的理念是坚持践行“立德树人”的任务,发展数学学科核心素养,以大概念为导向巧妙设计课内外的学习活动,整合交互课堂教学和课外作业,精读课标,尝试自主设计,注重作业质量,实现真正意义上的“减负增效”.

2 作业类型划分

根据属性分类:课堂作业、实践(项目)作业、预习作业、拓展作业、课后作业等.

根据形式分类:阅读作业、活动作业、背诵作业、书面作业等.

根据题型分类:客观题(单项或多项选择题、填空题)、主观题(解答题).

按难度划分:基础题、巩固题、拓展题等.

按时间划分:课时作业、单元作业、周末作业、假期作业等.

按人员划分:个人作业、小组作业、集体作业等.

按呈现方式划分:文字作业、图画作业、视频作业、语音作业、表演作业、演讲作业等.

3 单元作业实例

以人教A版普通高中教科书数学必修第一册“5.4三角函数的图象与性质”为例.课时内容为正弦函数、余弦函数、正切函数的图象与性质.

3.1 单元目标

(1)借助单位圆,精确地画出正弦、余弦、正切曲线,掌握描点法、五点法.

(2)体验绘制余弦函数、正弦函数、正切函数图象的过程,感受图象的具体变换.

(3)结合函数图象对函数性质进行分析探索,掌握余弦函数、正弦函数、正切函数的性质.

3.2 作业实例

本单元作业分自助选题、开放编题、知识导图、探究发现四个任务给出.

3.2.1 任务一:自助选题

(一)必做题

A.基础题

(2)周期函数f(x)(x∈R)的最小正周期是2.当x∈[0,2]时,f(x)=(x-1)2,求f(3)的值.

(3)求函数y=tan 3x的定义域.

B.巩固题

(1)下列函数中,哪些是奇函数?哪些是偶函数?

①y=1-cosx; ②y=-sinxcosx.

(2)观察正弦曲线、余弦曲线和正切曲线,写出满足如下条件的x所在的区间:

①sinx>0; ②cosx<0; ③tanx=0.

(3)求下列函数的最大值、最小值,并求取得最值时自变量的集合.

①y=2sinx,x∈R;

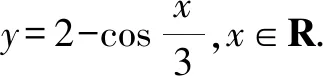
(二)选做题

C.发展题

A.0个 B.1个 C.2个 D.3个 E.4个

(2)在不求值的情况下,比较下列各组三角函数值的大小.

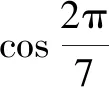
②tan(-52°)与tan(-47°).

(3)求下列函数的周期:

设计意图：自助选题作业分为必做与选做题,必做题中又分为A,B两类,A类巩固新知,B类借助图象加深对函数性质的理解,C类培养思维的灵活性与深刻性.可通过智学网统计错题,根据数据选取分析角度,确定讲评方法,形成错题题库.数学的分层作业,可让学生根据自己的需求自由选择组合,提高完成作业的积极性,体会到作业完成的快乐,让不同的学生得到不同的发展.学生在完成作业的过程中复习知识点,记录看不懂的问题及一些疑问,培养反思归纳能力.把解答过程完整写出来,交由教师审阅.当然,也可以自评或生生之间互评.随后反思错因或不同解法,并提出自己的观点及新问题的引申.

3.2.2 任务二:开放编题

(一)请你根据复习内容,自主出题或改变题目并解答,与同学相互交流.

设计意图：设置一题多变、一题多解、多题一解问题,比较不同的解法,让学生从不同的角度理解问题,寻求不同的解决途径,注重通性通法,找到不同表述方式的真正内涵,有层次地推进教学.回顾典型错误,勤于总结,激活学生思维,激励学生钻研.

(二)挑选开放性问题,注意与其他知识的综合.

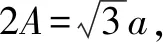
设计意图：适当植入开放性问题,为学生提供多元化选择,让他们在广阔的思维空间中获得对知识的深层理解.选择有把握的条件进行解答,勇于尝试,学会思考.设置问题时可开放情境,与生活内容接轨;开放内容,让学生善于选择.

3.2.3 任务三:知识导图

阅读课本,画出本节知识结构框图.

作业成果:(举例,如图1所示.)

图1

设计意图：学生按照自己的思维方式深入理解知识,从不同的角度多方位整理知识结构,快速理清思路,优化学习,促进知识的纵深发展.学生不断联想迁移,产生多种想法,培养思维习惯,相互交流,加深印象.

3.2.4 任务四:探究发现

探究1探讨函数y=Asin(ωx+φ)及函数y=Acos (ωx+φ)的周期(阅读课本第203～204页).

思考:(1)如何表示上述函数的周期?

(2)求周期的方法是否能推广到求一般周期函数的周期?

(3)求函数y=Atan(ωx+φ)的周期.

探究2紧扣单位圆的性质,进一步探讨余弦函数、正弦函数的性质(阅读课本第208～209页).

思考:结合单位圆,我们可以快速得出三角函数的定义,那么可以再次结合单位圆的性质,探析余弦函数、正弦函数的性质吗?查阅书籍或上网搜集相关资料,将你的研究方案和研究结果写下来.

设计意图：要求学生阅读教材,自我梳理归纳.换个角度认识性质,加深对函数性质的理解,通过探索提升学生发现和提出问题、分析和解决问题的能力,以及收集整理资料的能力.

4 结语

在设计高中数学大单元作业时,必须关注学生与学生之间的差异,紧扣单元重点,设计出多类型分层次的作业.同时,配套使用作业评价方式,持续延展学生学习空间,促进学生学习能力的提高.教师也需要不断学习,思考作业设计的意义,提高作业设计的水平,优化作业设计的路径,寻求作业设计的突破,让学生在作业中得到提升和收获.Z