融合注意力机制和LSTM的跳频抗干扰智能决策

靳 越,吴晓富,张剑书,2

(1.南京邮电大学 通信与信息工程学院,江苏 南京 210003;2.南京工程学院 计算机工程学院,江苏 南京 211167)

0 引言

随着通信对抗技术的快速发展,无线通信更易受到有意的干扰攻击,因此抗干扰通信一直是近几年通信领域的一个活跃研究课题[1]。在通信对抗中,对抗双方都需要动态做出决策来调整通信或者干扰策略,从而获得最大化的对抗收益。本文研究了抗干扰方的通信决策问题,目标是通过动态决策优化通信抗干扰的能力。

目前主流的通信抗干扰技术为直接序列扩频技术(Direct Sequence Spread Spectrum,DSSS)与跳频扩频(Frequency Hopping Spread Spectrum,FHSS)。其中,跳频通信由于其较强的抗干扰能力以及信号难以截获的特点,被广泛应用于抗干扰通信领域。

近年来,博弈论作为研究对抗性游戏的数学工具也在通信对抗中得到了广泛应用。博弈论主要研究具有竞争性质的不同个体间的相互作用过程,考虑竞争过程中个体间的预测行为和实际行动,制定相应的优化策略。随着人工智能以及通用无线电外设(Universal Software Radio Peripheral,USRP)的高速发展,干扰方可以动态发起更为智能的干扰攻击[2],然而博弈论对动态决策并不是非常适合。

在人工智能领域,强化学习(Reinforcement Learning,RL)被认为是解决动态决策的有效工具。目前,强化学习中的Q网络技术是解决该动态环境下决策问题的有效方法,并且已经广泛应用于各种抗干扰通信决策问题。文献[3]利用Q网络算法研究了单个用户模式下的通信抗干扰问题。Q网络一般用于处理状态数受限的决策问题, 鉴于通信抗干扰的基于频谱瀑布的状态定义涉及的状态数不受限,因此Q网络一般不能直接处理抗干扰通信决策中的频谱瀑布输入问题[4-5]。

近年来,强化学习与深度学习相互融合取得了里程碑式的结果,即深度强化学习(Deep Reinforcement Learning,DRL)。2013年,谷歌团队提出了第一个DRL算法,即深度Q网络(Deep Q Network,DQN)算法。该算法通过引入深度神经网络来近似Q网络,在多个Atari游戏中获得优异的成绩。DQN算法作为DRL的经典算法,受到了国内外学者的广泛关注。文献[6]提出了深度双Q网络(Double DQN,DDQN),解决了DQN算法中Q值高估的问题。文献[7]提出了竞争Q网络 (Dueling DQN)算法,通过改变决策神经网络,将Q值拆分为状态价值函数与相关状态下特定动作的优势函数之和,提高了Q值预测的准确性。文献[8]提出了包含噪声的深度Q网络(NoisyNet DQN)算法,在网络中加入噪声网络,提高了算法的稳定性和探索性。此外,还有其他系列的改进方法,包括优先经验回放、DRQN、Rainbow算法等[9-11]。

基本的DQN算法具有模型简单易于实现的优点,但对于动态决策而言决策网络的模型收敛速度过于缓慢。针对这种情况,本文提出通过注意力机制与长短时记忆(Long Short-Term Memory,LSTM)层的有效结合来解决抗干扰通信背景下的时频特征高效提取与学习问题。此外,除了静态干扰模式,本文也从实际角度考虑,设置了动态干扰模式。因此本文提出的基于注意力机制和LSTM结合的DQN通信抗干扰算法,在原始DQN算法基础上,考虑了干扰信号频谱瀑布的分布规律与时间特征,从而通过注意力模块与LSTM网络更加全面地获取信息,极大地加快了模型收敛的速度[12-13]。

1 系统模型

1.1 信号传输模型

如图1所示,在t时刻,考虑一个合法通信用户对(发送方与接收方)受单个干扰机影响的场景:t时刻,在Agent的引导下,合法通信用户对的发送方可以选择一个频点(用f(t)∈[fL,fU]表示,其中fL、fU分别表示用户通信频段的起始和终止频率),以pu表示发送信号功率。

图1 信号传输模型Fig.1 Signal transmission model

用户与干扰机通过电磁环境持续进行交互,利用环境反馈结果并结合通信抗干扰决策算法持续更新算法模型参数直至模型完全收敛,考虑到干扰信号和合法通信用户对信号以及噪声的共存,设Agent在时间间隔[t,t+Δt]接收信号的短时信号功率谱密度(Power Spectral Density,PSD)函数可表示为:

(1)

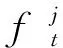
考虑到在实际的频谱感知中,Agent感知并计算短时离散PSD,即:

(2)

式中:Δf为频谱分析的分辨率。

1.2 通信抗干扰决策的深度强化学习建模

由于电磁环境本身叠加了合法用户信号、干扰信号以及多径传输等影响,Agent感知的电磁频谱信号很难直接用于通信抗干扰决策。而深度强化学习具有从电磁频谱中学习干扰对抗态势的能力,在单智能体假设下可以将通信抗干扰决策问题建模为马尔可夫决策问题(Markov Decision Processes,MDP),而强化学习则是求解该MDP问题的利器[14]。

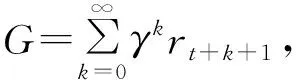
强化学习的目标是:找到一个最优策略π*,使得该策略下的累计回报G期望最大。

深度强化学习是指通过深度神经网络来拟合决策函数π并通过深度学习方法解决最优策略π*的求解问题。

令gu表示从发射机到接收机信道功率增益,gj表示从干扰机j到接收机的增益。则合法用户的接收SINR可以表示为:

(3)

令βth表示成功传输所需的SINR阈值,归一化的传输率可以表示为μ(ft)=δ(β(ft)≥βth),若β(ft)≥βth为真,则μ(ft)=1,否则为0,即当接收SINR超过阈值时,μ(ft)=1表示信息成功传输,r为即时奖励函数,定义为:

r(at)=μ(at)-λδ(at≠at-1),

(4)

式中:λ表示用户中心频率的切换成本。

1.3 干扰信号模型与奖励函数

本文同时考虑了静态干扰和动态干扰。其中,静态干扰包括:① 梳状干扰——干扰机选择在2、10、18 MHz三个频率组成梳状谱干扰;② 扫频干扰——扫频速度为1 GHz/s。动态干扰包括:① 动态扫频/梳状随机干扰——干扰机以每100 ms周期等概率随机选择扫频干扰和梳状干扰模式;② 动态梳状干扰——干扰机以每1 000 ms周期等概率随机在2、6、10、14、18 MHz中选择三个频率组成梳状谱干扰。图2给出了两种动态干扰的短时时频图。

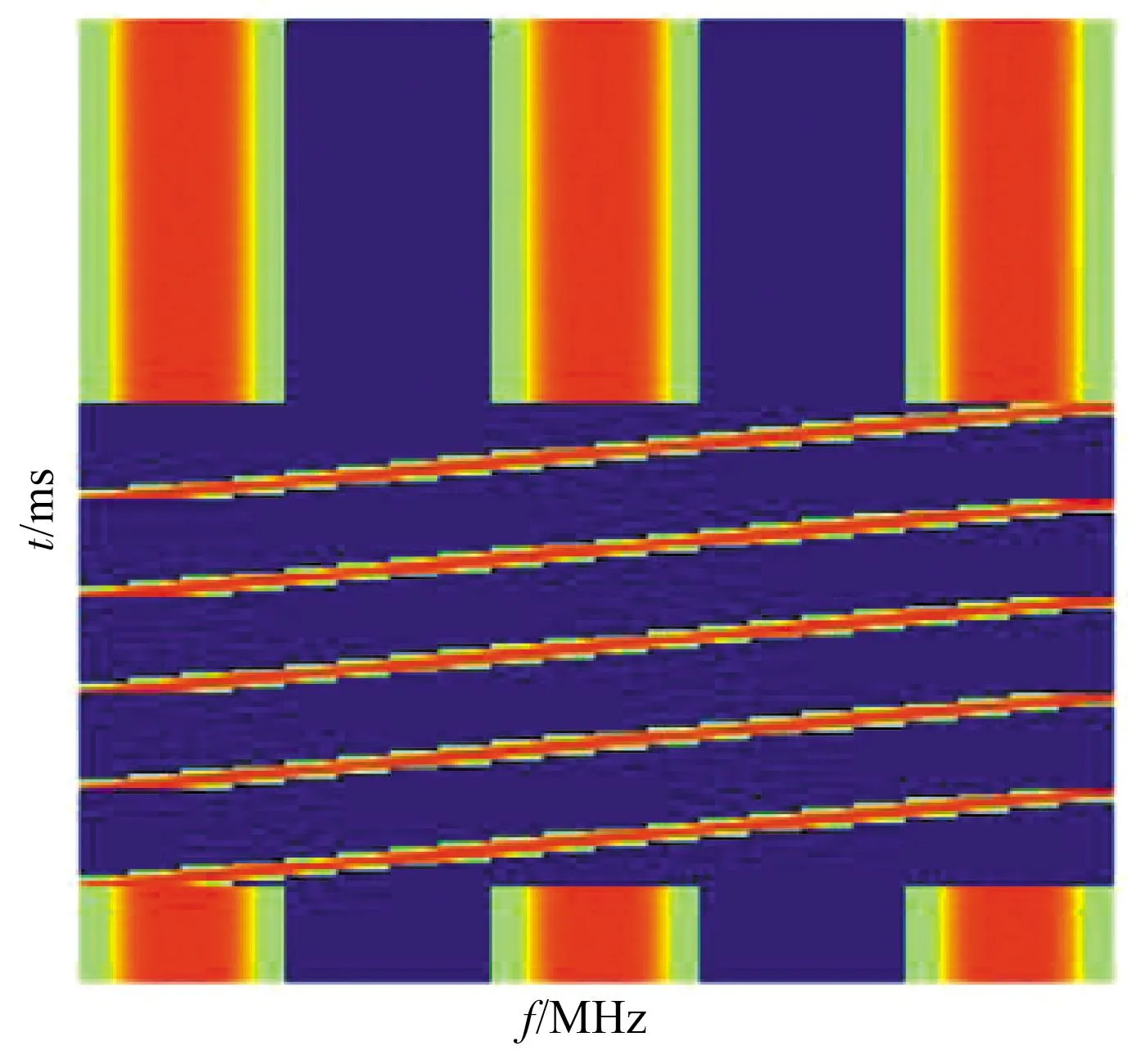
(a) 动态扫频/梳状随机干扰

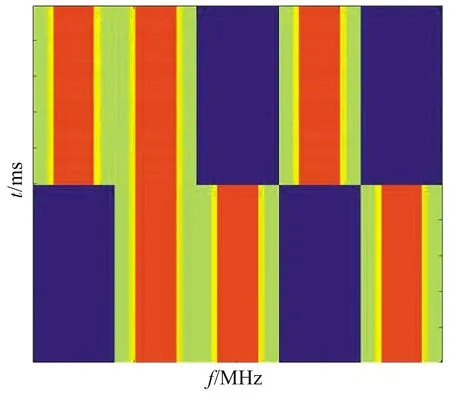
(b) 动态梳状干扰图2 两类动态干扰模式Fig.2 Two types of dynamic jamming modes

2 融入注意力机制和LSTM的决策网络设计

注意力机制已广泛运用于图像处理分析,本文考虑了三种注意力机制用于设计并进行了对比,包括SENet、通道注意力模块(Channel Attention Module,CAM)与空间注意力模块(Spatial Attention Module,SAM)。

2.1 注意力模块

从2014年起,注意力机制首先应用于机器翻译领域并随后在计算机视觉领域被广泛使用并以此提高深度神经网络的性能。注意力机制具有类似人类视觉的功能:人类视觉更倾向于图像中有助于判断的部分信息而忽略其他无关信息。如对图片中的物体进行分类,占据图片大部分面积的背景部分被视为无关信息。应用于计算机视觉领域的注意力机制一般分为通道域注意力、空间域注意力和混合域注意力。

2.1.1 SENet

SENet中通过SE模块来实现特征重标定,该模块包含以下三个操作:Squeeze、Excitation、Scale。SENet结构如图3所示[16]。

图3 SENet结构Fig.3 SENet structure

设该模块的输入为X,通过一系列卷积实现特征变换Ftr,即:

Ftr：X→U,X∈RH′×W′×C′,U∈RH×W×C。

(5)

设V=[v1,v2,…,vc]表示一系列卷积核,其中vc为第c层卷积的参数,则输出特征U=[u1,u2,…,uc]可由式(6)表示:

(6)

输出特征U进入 Squeeze操作,即平均池化:

(7)

式中:下标c表示第c维。因此将H×W×C的输入转换成1×1×C的输出,对应Squeeze操作。

运用SE模块中的Excitation操作来全面捕获通道依赖性,学习到通道之间的非线性关系,因此在Excitation操作中采用了Sigmoid形式的门控机制,通过W来为特征图的每一个通道生成相应权重:

s=Fex(z,W)=σ(W2δ(W1z))。

(8)

采用了参数分别为W1和W2的两个全连接层来提升网络的泛化能力,将得到的1×1×C的实数结合原始特征图通过SE模块中的Scale进行输出,即:

(9)

2.1.2 通道注意力

CAM结构如图4所示,其与SENet的不同之处是加了一个并行的最大池化层,提取到的高层特征更全面,更丰富[17]。

图4 CAM结构Fig.4 CAM structure

给定输入特征F,CAM做以下运算:

Mc(F)=σ(MLP(AvgPool(F))+MLP(MaxPool(F)))=

(10)

式中:MLP为全连接层,AvgPool表示平均池化,MaxPool表示最大池化,W1、W2为全连接层权重。

输入特征F经过两个并行的最大池化层和平均池化层,将特征图从H×W×C变为1×1×C的大小,然后经Shared MLP模块,在该模块中,先将通道数扩张为原来的r倍,再压缩到原通道数,经过ReLU激活函数得到两个激活后的结果。将这两个输出结果进行逐元素相加,再通过一个Sigmoid激活函数得到通道注意力的输出结果,再将这个输出结果乘以原图尺寸,得到大小为H×W×C的输出。

2.1.3 SAM

单纯的SAM比较简单,其实现以下功能:

Ms(F)=σ(f7×7([AvgPool(F);MaxPool(F)]))=

(11)

SAM结构如图5所示,输入特征F通过最大池化和平均池化可以得到两个H×W×1的特征图,然后经过连接操作对两个特征图进行拼接,通过7×7卷积变为1通道的特征图,再经过一个Sigmoid得到空间注意力的特征图,最后将输出结果乘原尺寸变回H×W×C大小。

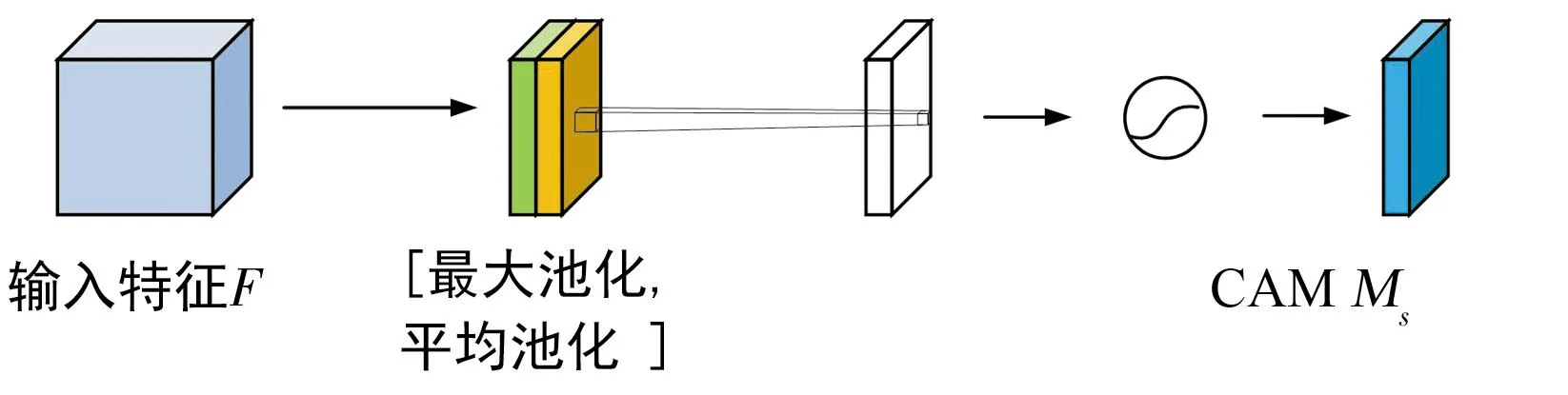
图5 SAM结构Fig.5 SAM structure

2.2 LSTM模块

循环神经网络 (Recurrent Neural Network,RNN) 是一类用于处理序列数据的神经网络。然而RNN在训练时会产生梯度消失或梯度爆炸问题。为了解决这个问题,LSTM应运而生[18]。LSTM结构是一种特殊的循环神经网络结构,通过“门”来控制信息的增加或丢弃,LSTM结构可以处理序列信息并且提取时间特征,解决了长时间序列的信息传递问题,使其具备长期记忆功能。LSTM模块如图6所示,数学原理如式(12)。

图6 LSTM模块Fig.6 LSTM module

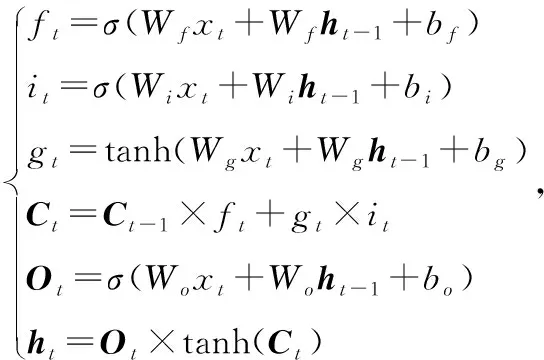
(12)

式中:W均为权重,b均为偏置,Sigmoid与tanh为激活函数。

LSTM有三个Sigmoid门,自左向右依次是遗忘门(f)、输入门(i)、输出门(o)。由于Sigmoid函数将输入映射到(0,1)区间的特点,这三个门分别决定了长期记忆流的保留程度、输入单元的嵌入程度和短期记忆流的呈现程度。其原因很容易理解,如果Sigmoid输出为1代表信息完全保留,输出为0代表信息完全丢弃,而在0和1之间则代表了信息不完全保留而有所丢弃。

LSTM中还有按位乘法与加法两种操作。按位乘法操作也就是遗忘门所执行的操作,用于丢弃部分信息;具体操作为:Sigmoid函数和细胞状态Ct-1执行按位乘操作。Sigmoid函数的输出为0～1的向量x′。使用向量x′去按位乘Ct-1向量,显然会使得Ct-1向量的每一位置的值不同程度变小。从这样的角度来看,Ct-1向量的部分值变小,就相当于“信息”被丢弃了。而“加法”操作,可以用于添加新的信息。具体操作为:使用一个Sigmoid函数,用此函数来按位乘隐藏状态、输入x的拼接向量[ht-1,x],此时Sigmoid函数的作用是选择性的获取隐藏状态和输入x中的信息。随后的加法操作则是将这部分信息加入到了细胞状态的向量中。

2.3 融入注意力和LSTM的DQN设计

为具体起见,设抗干扰决策场景的跳频范围为20 MHz,感知周期为200 ms,故将尺寸为200×200的频谱瀑布图作为决策输入。

本文提出的Attention+LSTM+DQN网络模型如图7所示。

步骤1:将200×200的矩阵再次以频率轴分割,转化成200个尺寸为200×1的时间序列向量作为LSTM模块输入。输出为经过LSTM模块处理后的200×300的矩阵。

步骤2:将大小为200×300的频谱瀑布图通过CAM模块,经过平均池化与最大池化后经过Shared MLP模块输出为1×1×C,再将该输出乘以原图尺寸,得到1×200×300的输出。

步骤3:将步骤2中输出的三维tensor展平至一维数据,再经过两个全连接层,得到输出是大小为9的向量。网络参数如表1所示。

表1 网络参数Tab.1 Network parameters

3 仿真实验

3.1 实验流程

所设计DQN的训练和测试均在Linux服务器上进行,语言环境为Python3.7,CPU为Intel(R) Xeon(R) Silver 4210 2.80 GHz,GPU为NVIDIA Corporation GK210GL [Tesla K80]。

3.2 仿真条件

本文实验基于Pytorch深度学习架构进行系统仿真和实验分析。实验中的场景是前文中的干扰模型。将三种抗干扰决策方法进行对比:DQN、LSTM+DQN与本文提出的Attention+LSTM+DQN。实验参数设置如表2所示。

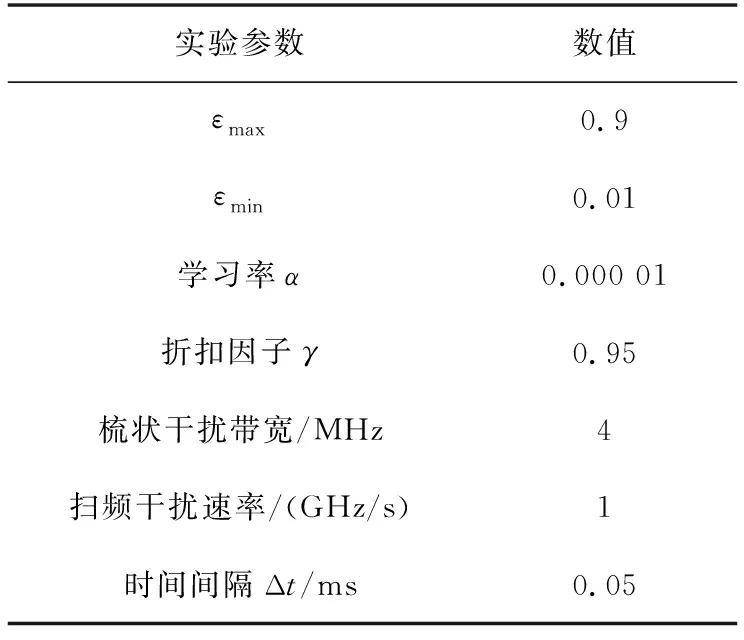
表2 实验参数Tab.2 Experimental parameters

3.3 仿真结果与分析

为评估决策网络的训练收敛能力,实验中网络训练一轮后,立即用当前模型进行评估,这样设置可以实时看到模型的在线训练效果以及收敛速度。

选取SENet+LSTM+DQN、SAM+LSTM+DQN和LSTM+DQN作为CAM+LSTM+DQN的对比模型。其中SENet+LSTM+DQN与SAM+LSTM+DQN为图7模型中将CAM注意力层替换为SENet注意力层与SAM注意力层构成的模型;LSTM+DQN为图7中去除CAM注意力层后构成的模型。

本文将5次独立实验的结果取平均得到实验对比图。对于较为简单的梳状干扰与扫频干扰,设置了8轮训练与评估,对于较为复杂的动态干扰,设置了20轮训练与评估。

3.4 抗干扰性能分析

本文利用归一化的吞吐量来衡量网络的性能。在仿真中Epoch定义为深度决策网络迭代训练100次,具体操作过程如下:第一步训练神经网络:神经网络训练一个Epoch;第二步保存神经网络权重;第三步测试神经网络:利用第二步保存的神经网络权重在相同的干扰模式下验证一个Epoch,并计算归一化吞吐量Tall。

在一轮评估中,归一化吞吐量Tall等于这一轮评估中奖励值大于0的总次数除以这一轮评估的总次数,即:

Tall=Nreward/Nall,

(13)

式中:Tall为归一化吞吐量,Nreward为奖励值大于0的次数,Nall为评估总次数。在实验中设置Nall=100。

三种干扰场景下不同抗干扰算法的性能对比如图8所示,可以看出,没有加入LSTM层处理的DQN的算法性能最差,以梳状干扰为例,在训练8个Epoch后模型才达到收敛,而仅加入了LSTM层的LSTM+DQN与Attention+LSTM+DQN在一轮训练后就已经到达收敛。

(a) 梳状干扰

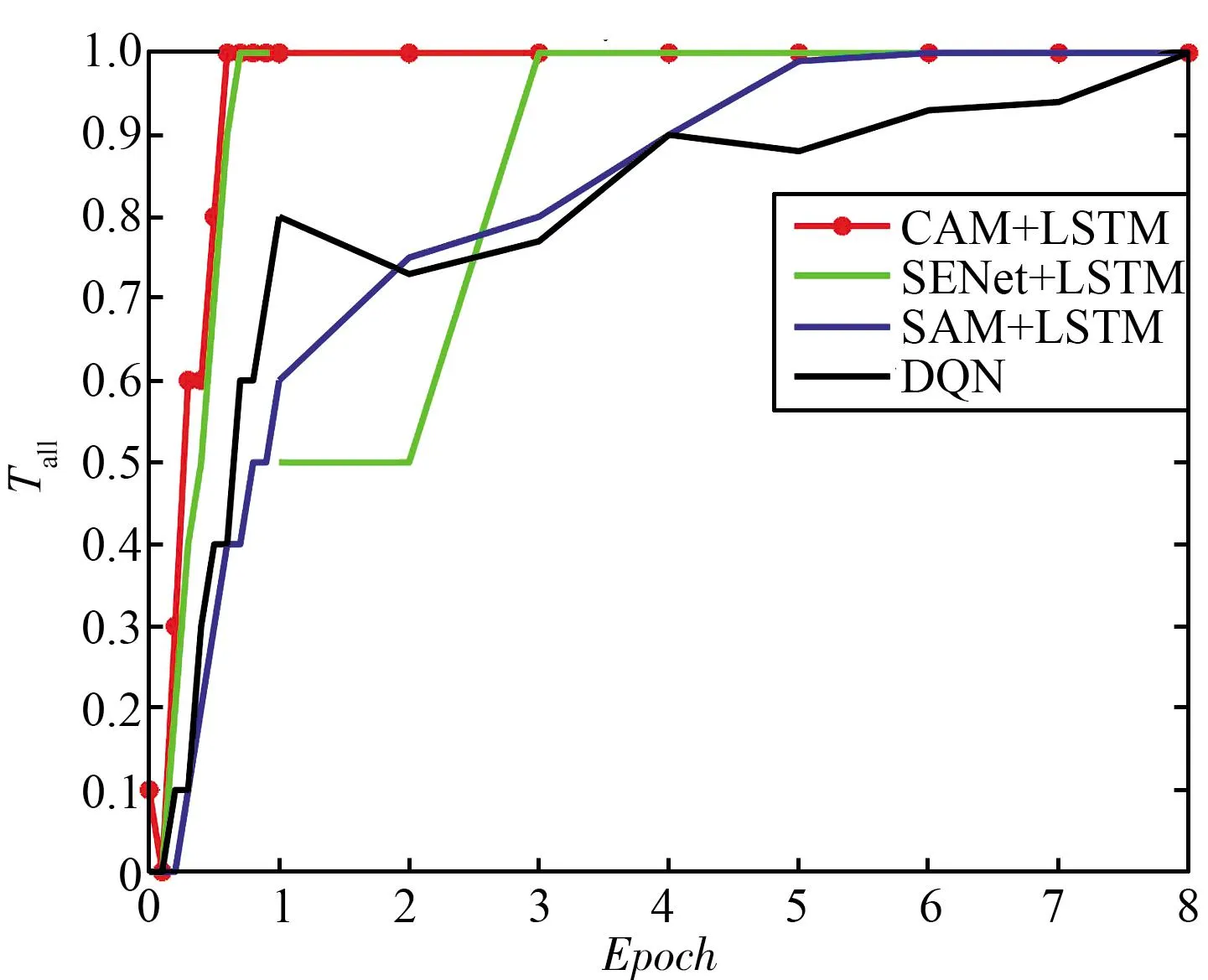
(b) 扫频干扰图8 静态干扰下不同抗干扰决策网络的性能对比Fig.8 Performance comparison of different anti-jamming decision networks under static jamming

图8中的干扰环境处于静态模式下,在实际中,干扰并不是一成不变的。图9中的干扰均为动态干扰模式,对于动态扫频/梳状干扰,本文提出的决策网络在1轮训练后已经达到了较高的吞吐量,完成了收敛。而LSTM+DQN算法与DQN算法则分别需要5轮训练与10轮训练,对于动态梳状干扰,可以看出Attention+LSTM+DQN算法仍然优于所有其他算法。综上可以看出所设计决策网络具有最快的收敛速度,证明了该算法在复杂动态场景下也具有较好的性能,具有鲁棒性。

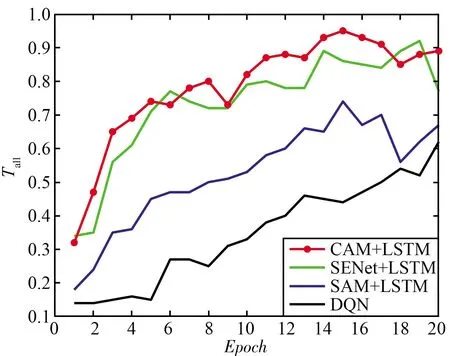
(a) 动态扫频/梳状干扰

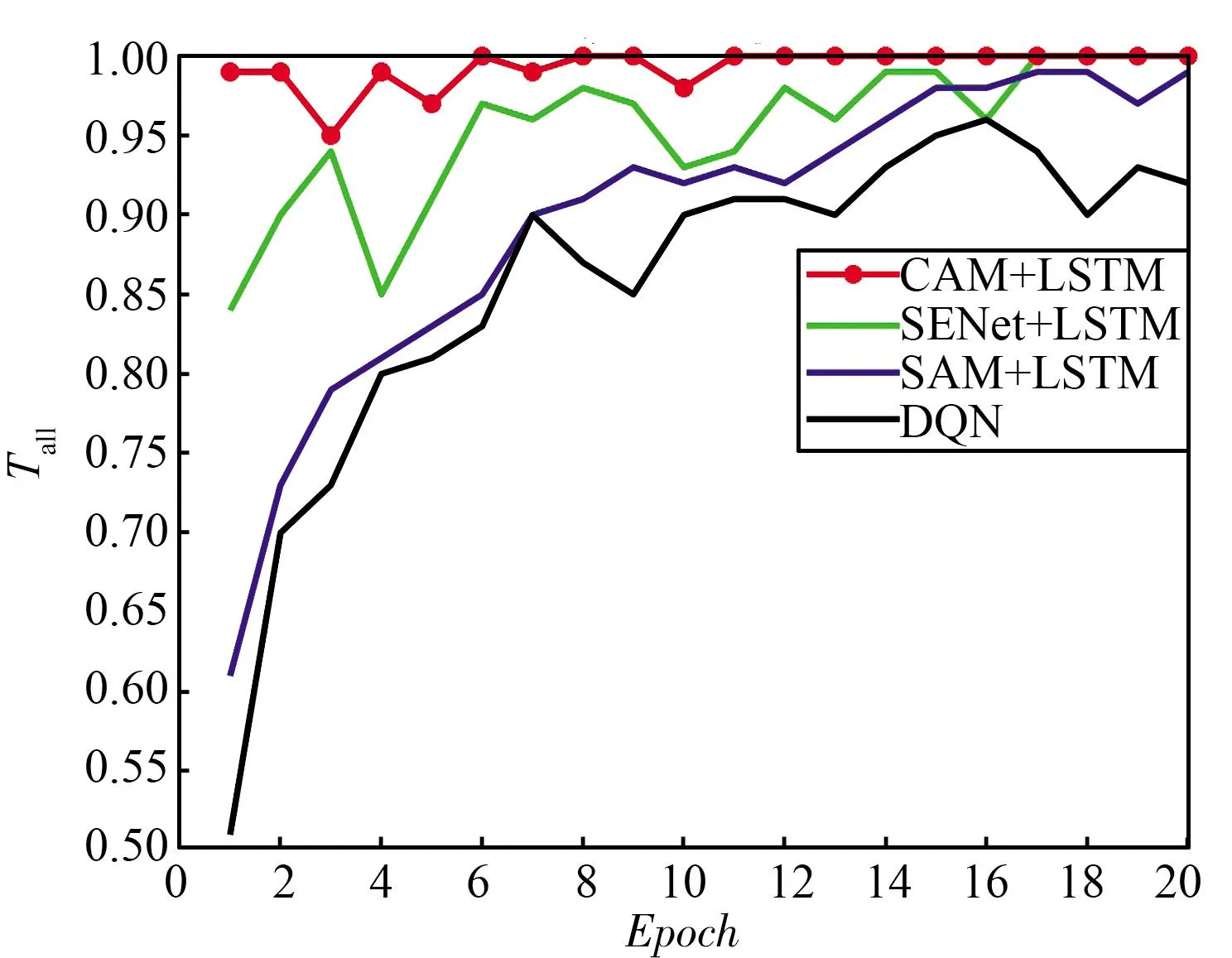
(b) 动态梳状干扰图9 动态干扰下不同抗干扰决策网络的性能对比Fig.9 Performance comparison of different anti-jamming decision networks under dynamic jamming

此外评估中的奖励值也可以评估算法是否优秀。强化学习模型的训练以最大化累积奖励为目标,累积奖励越大,模型的性能越好。评估总奖励对比如图10所示,可以看出,所提出的决策网络较其他两种网络均有较高的累积奖励,说明其性能最佳。

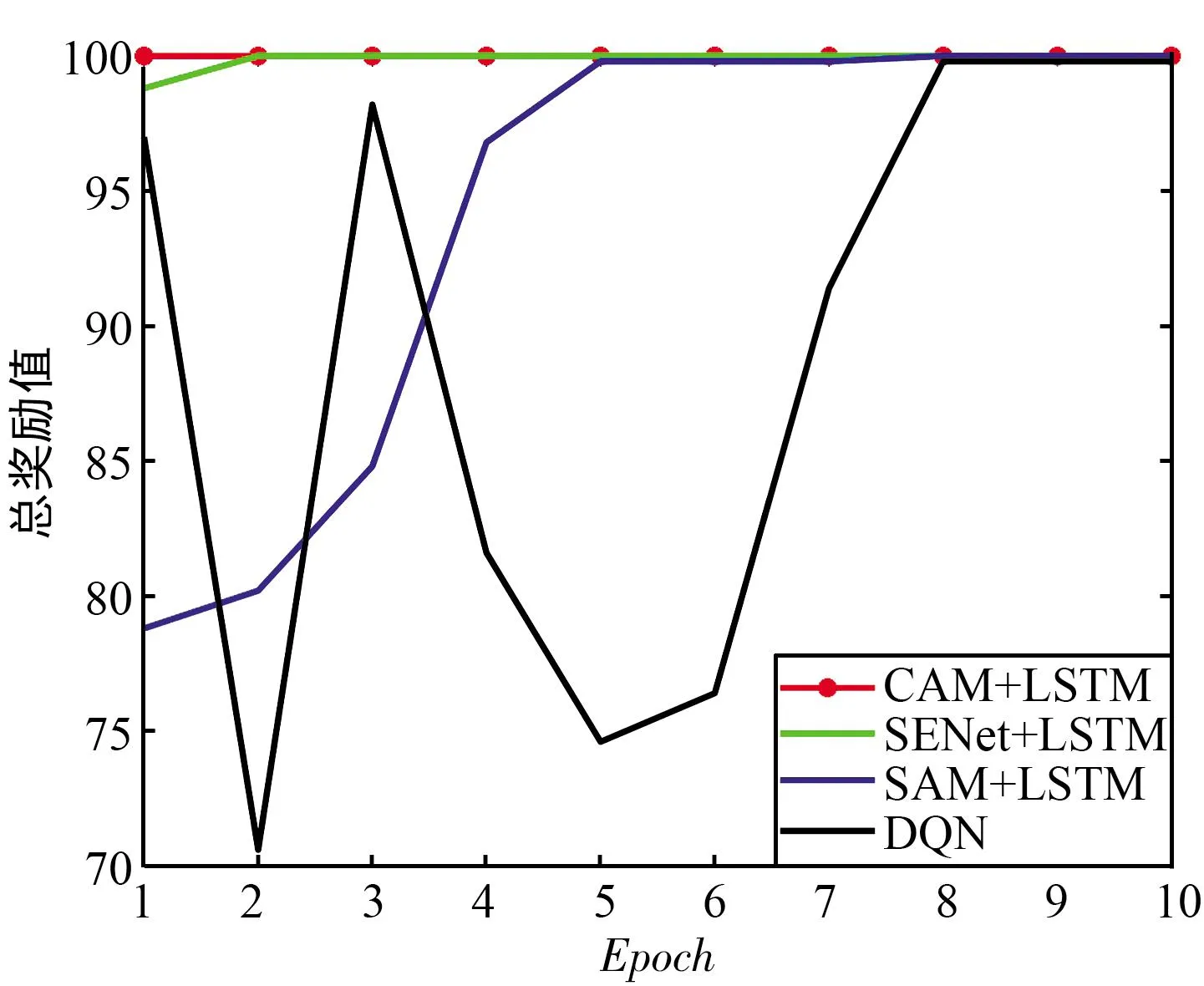
(a) 梳状干扰奖励值

(b) 扫频干扰奖励值图10 评估总奖励对比Fig.10 Comparison of total rewards for evaluation

4 结论

本文主要研究跳频场景中的抗干扰决策网络设计问题。通过融入注意力模块与LSTM模块,所设计的深度决策网络适用于多种干扰模式下的抗干扰跳频决策。仿真结果表明,在不同的干扰模式下,该算法表现出优异的在线收敛速度以及收敛性能,有利于在动态干扰环境下进行快速决策。