压力容器中边缘应力和局部高应力叠加影响研究

欧金藩

（湖南化工设计院有限公司，湖南长沙 410007）

筒体和封头都是压力容器中的重要组成部件，筒体和封头连接时的边界效应会产生分布复杂的边缘应力[1]。另外，压力容器中一般都存在壳体开孔结构，开孔接管与筒体相贯区会出现局部高应力。在设计中，时常会出现开孔离筒体和封头连接处很近的情况，比如热交换器中封头管箱的开孔；筒体和封头连接处边缘应力和开孔接管与筒体相贯区局部高应力会相互影响。为了避免两种应力的叠加影响，相关文献中提出开孔边缘和筒体与椭圆形封头连接处的最小距离W宜取和3δn两者中的较大值（其中：Dn为容器公称直径，δn为容器壳体名义厚度）[2]。本文将采用有限元应力分析法，对不同的模型（开孔率不同，开孔和筒体与封头连接处距离不同）应力强度情况进行计算和对比，探究筒体与封头连接处边缘应力和接管与筒体相贯区局部高应力叠加影响情况。

1 设计参数及结构尺寸

设计参数及壳体尺寸：设计压力1.1MPa，设计温度50℃，内径600mm，名义厚度6mm，材料为S30408。壳体厚度不考虑厚度附加量，文献[2]中所提最小距离W为150 mm。

结构几何简图如图1。按开孔接管公称直径为DN100、DN150、DN200、DN250、DN300五种规格，每种开孔接管规格的结构又分W＇＜W和W＇＞W两种情况（其中W＇如图1所示），分别建立模型进行有限元应力分析。

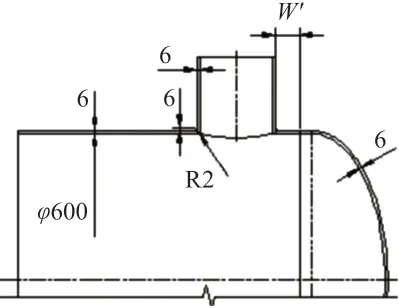
图1 结构简图

2 有限元分析计算

2.1 计算模型

由于模型结构和载荷均具有对称性，取整体结构的1/8作为分析模型。

模型网格划分如图2所示。

图2 模型网格划分

2.2 载荷和边界条件

在筒体端部横截面施加轴向位移为零的约束，在对称面施加对称约束。容器内表面施加1.1 MPa 的压力，接管端面施加内压对应的等效平衡载荷p1，p1按下式计算。

其中，p、di、δnt分别为容器内压、接管内径及接管壁厚。

2.3 计算结果

不同开孔接管公称直径和不同W′值的计算模型（共10种）的有限元计算应力云图如图3~图7。从图中可以看出，同一开孔直径的两模型对比，W'值小的，应力强度更大；且随着开孔直径的增大，W'值不同时，应力强度相差越大。

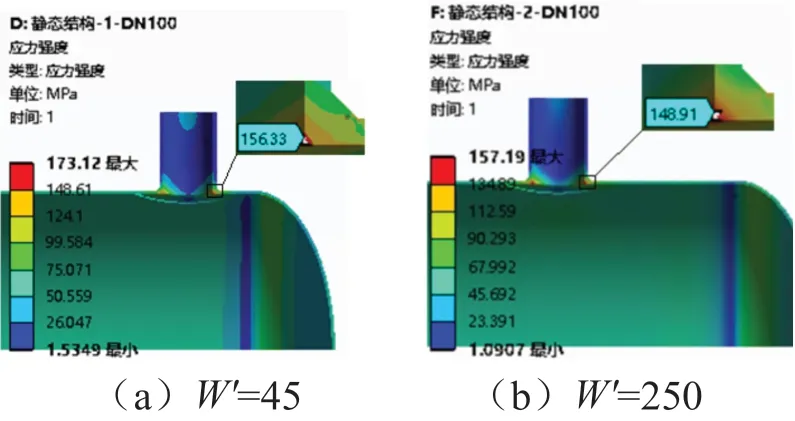
图3 开孔接管为DN100，两种W′值的应力云图

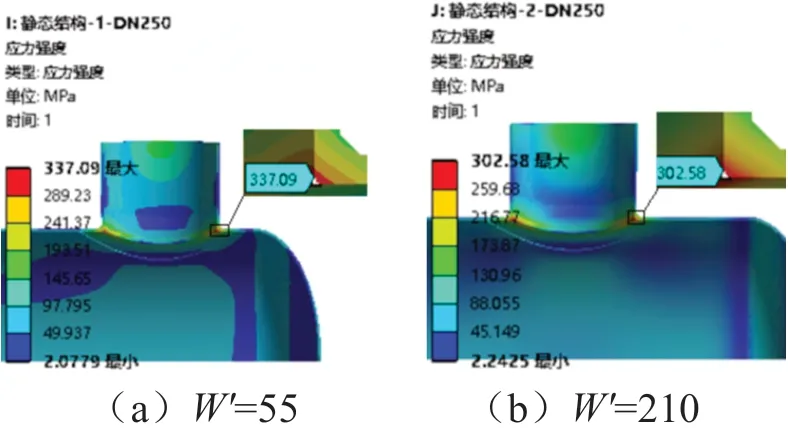
图6 开孔接管为DN250，两种W′值的应力云图

图7 开孔接管为DN300，两种W′值的应力云图

3 应力等效线性化及应力强度分析

应力分类参照JB 4732—1995（2005年确认）《钢制压力容器分析设计标准》。应力等效线性化的路径选取原则为：对分析部位，沿厚度最小方向取路径。

计算结果中有些模型最大应力出现在焊缝与筒体外壁连接处，该处峰值应力占比较大，故本文对该处不作讨论。对每个模型按图8所示的四条路径进行应力等效线性化处理。由于考察的是静载荷作用下的应力强度，表1中列出了每个模型各路径上一次局部薄膜应力强度SⅡ和一次局部薄膜应力加二次弯曲应力强度SⅣ。

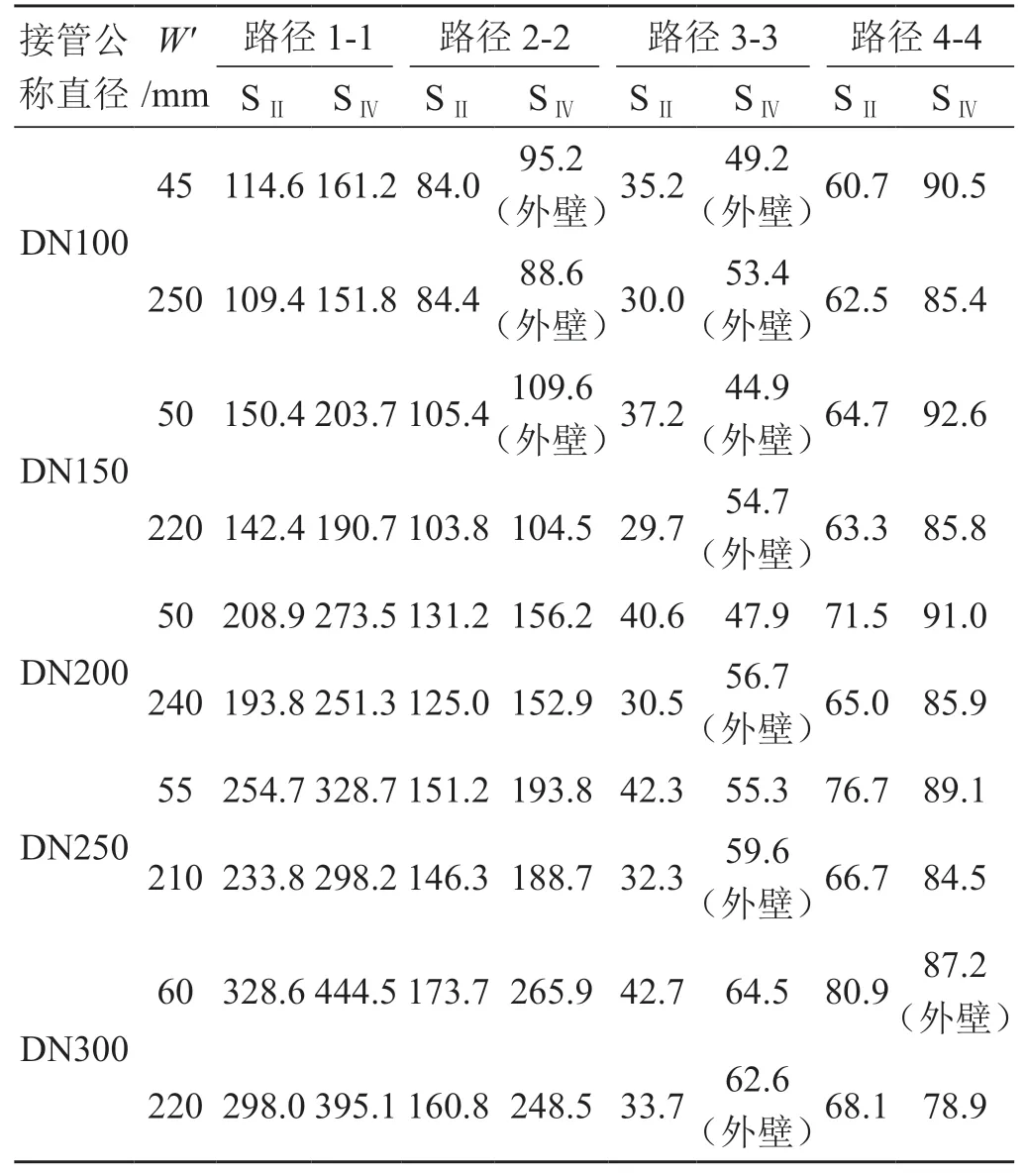
表1 各路径上的应力强度

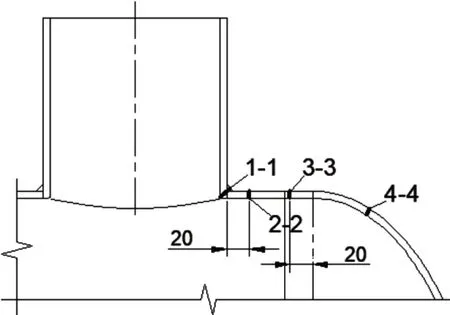
图8 应力等效线性化路径

下面探讨同一开孔直径（开孔率）时W′＜W和W′＞W两种模型各路径上SⅡ的相差百分比δ，以及相差百分比δ的值随着开孔率变化的规律。如图9所示。从图9可以看出，随着开孔直径的增大（开孔率增大）W′＜W的模型的应力强度SⅡ超出W′＞W的模型的应力强度SⅡ的百分比逐渐增大。

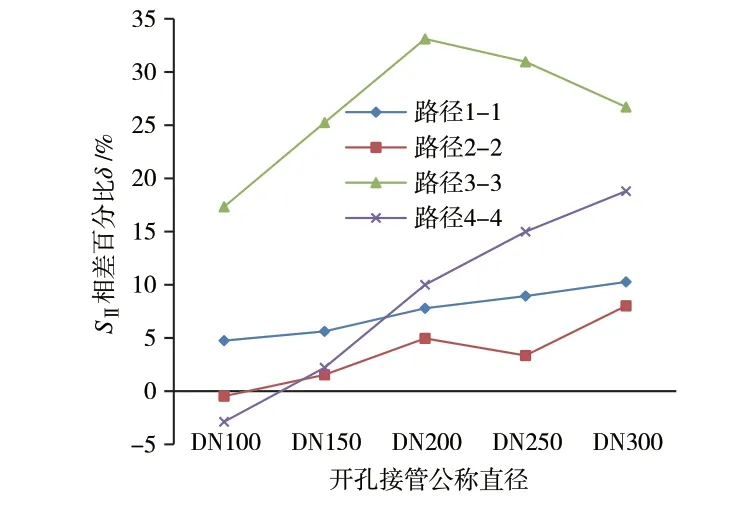
图9 SⅡ相差百分比δ随开孔率变化情况

从图9还可以看出，路径3-3处的SⅡ相差百分比δ的值一直处于比较高的水平，即筒体上开孔距离筒体与封头连接处较近时对路径3-3处的应力强度有明显的影响，但是路径3-3处应力强度水平较低，所以此处应力强度的增大并不会对壁厚的取值形成影响。路径2-2处SⅡ相差百分比δ处于比较低的水平，即筒体与封头连接处的边缘应力对开孔壳体补强区域应力强度的影响较小。路径1-1和路径4-4处SⅡ相差百分比δ随着开孔接管直径由DN100逐次增大到DN300（开孔率ρ由0.16逐次增大到0.52）逐渐增大，即开孔率越大，筒体与封头连接处的边缘应力对接管与筒体相贯区应力强度的影响越大，以及接管与筒体相贯区局部高应力对封头过渡区应力强度的影响越大。

4 结论

1）筒体与封头连接处的边缘应力和接管与筒体相贯区的局部高应力会叠加影响，开孔率越大，相互影响越大，当开孔率ρ达到0.52时，接管与筒体相贯区的一次局部薄膜应力SⅡ受筒体与封头连接处边缘应力的影响会增大10.27%，封头过渡区的一次局部薄膜应力SⅡ受接管与筒体相贯区高应力的影响会增大18.8%。

2）在常规设计中，开孔边缘和筒体与封头连接处的距离尽量大于文献0中提出的最小距离W。在无法保证该距离大于W时，开孔补强面积及封头厚度应保有足够的裕量。