Gaussian和Multiwfn软件在计算制冷剂介电常数中的应用*

马 跃，吴学秋，杨 敏，宋卫余

(中国石油大学(北京)理学院，北京 102249)

物理化学是在物理和化学基础上发展起来的一门学科。它以丰富的化学现象和系统为对象，吸收大量物理学的理论成果和实验技术，探索、总结和研究化学的基本规律和理论，形成化学科学的理论基础[1-3]。物理化学的主要研究内容之一是化学体系的微观结构和性质，研究分子、分子簇和晶体的结构，以及结构与物理性质之间的关系和规律。

随着量子化学计算的发展，越来越多的计算化学技术应用于研究与教学中[4-6]。与传统的物理化学课堂教学相比，计算化学辅助物理化学教学模式允许学生自主参与和操作。物质的性质取决于其分子的性质，我们对分子的性质了解得越多，就越能理解该物质表现出的特征和现象。分子可视化和量子化学计算软件的发展提供了一个巨大的优势，它能够将分子的立体构型、电子轨道等化学信息具象化。传统模式下知识的讲解比较抽象，学生借助分子可视化软件，可以直接操作模拟，以拓展理论知识的深度。同时，物理化学与量化计算的有效结合，可以使学校教学资源得到更充分、更合理的利用。

氢氟碳化合物(HFCs)是一类强效温室气体，具有很高的全球变暖潜能值(Global warming potential，GWP)，目前被用作空调系统的制冷剂。全球升温潜能值的不断增长和人们对制冷剂的需求之间日渐矛盾，促使人们转向对“第四代”制冷剂的研究[7]，包括天然制冷剂[8]、不饱和氟化烯烃[9]和混合制冷剂[10]。我国的制冷剂发展方向是开发零ODP、低GWP值制冷剂和低GWP值HFCs，并且积极寻找HFCs的新应用，加强新一代环境友好制冷剂的原创力度。尽管新型制冷剂在低环境影响方面前景看好，但其热物理性质的广泛表征对于有效地将其应用于现有系统和优化新设计非常重要[11]。

在物理化学中，液体的介电常数是一个重要的物理特性，可以表示出溶剂化能力[12]，是评估制冷剂的主要参考值。传统意义上，介电常数(ε)定义为与给定系统的势能(V)相关的常数，与一个孤立的点电荷q1和另一个试验电荷q2的电荷值相关，由两个电荷的径向距离r分隔[13]：

(1)

相对介电常数εr是材料介电常数与真空介电常数之比[14]：

(2)

介电常数越大的液体，溶剂化能力越强。在测量介电常数的实验中，通常采用电容法，通过处理电路将电容的变化转为和液体相对介电常数有线性关系的电压值，变为直流电压后显示在电压表中[15]。但实验设计中，检测装置往往比较复杂。对制冷剂的性质测量，高电阻和介电常数测量的巨大灵敏度也具有挑战性[16]。特别是介电常数对外部影响(如局部电容、杂质)非常敏感。另一方面，用于计算介电常数的电容检测需要交流电。因此，必须根据所需的实验参数重新设计测量单元，包括：两个电极的热控制(-30～90 ℃)和耐压性(制冷剂压力高达80 bar)。

对于原子或低极性的分子，Clausius-Mossotti关系可以描述介电常数与分子极化率体积的关系：

(3)

式中：M表示摩尔质量，ρ表示密度，NA表示阿伏伽德罗数，α’表示物质的极化率体积。因此，如果材料的密度已知，通过密度泛函理论(DFT)计算估计的极化率体积可以预测分子的介电常数。

本文以计算制冷剂氟化液分子的介电常数为例，简述Gaussian和Multiwfn软件的计算原理和过程，探究量子化学计算在物理化学教学中的实践与应用。

1 Gaussian和Multiwfn软件简介

Gaussian是使用最广泛的量子化学软件[17-19]，可以用于研究许多化学领域的课题：分子能量和结构，过渡态的能量和结构，化学键以及反应能量，分子轨道，偶极矩和多极矩，原子电荷和电势，振动频率，红外和拉曼光谱，NMR，极化率和超极化率，热力学性质，化学反应机理，势能曲面和激发能等。

Multiwfn是一个多功能的波函数分析程序[20]，主要功能有计算和可视化真实空间函数，轨道组成分析，绘制状态密度和光谱等。还提供了量子化学研究中涉及的一些其他有用的实用程序。内置图形模块可直接绘制波函数分析结果或导出为高质量图形文件。程序界面非常友好，适用于研究和教学目的。Multiwfn的代码得到了充分的优化和并行化。其效率明显高于具有相同功能的相关程序。

2 介电常数计算的实验步骤

本文使用Gaussian 09软件包[21]，选择使用B3LYP杂化密度泛函[22]，为了考察不同基组预测介电常数结果的精确性，我们考虑了三种不同的基组6-311G，6-311+G和6-311G(3df，2p)，选择三个不同的氟化液分子进行测试。表1中给出了三个氟化液分子介电常数的实验值与其在不同基组下的计算值。通过比较发现，B3LYP/6-311+G(3df，2p)基组下的计算值偏差相对最小。

表1 三种氟化液分子介电常数的实验值和不同基组下的计算值

(1)构建分子模型。以全氟正戊烷(商品名FC-87)为例，学习使用GaussView构建全氟正戊烷分子模型，将结构文件保存为FC-87.cif格式。

(2)结构优化。采用Gaussian 09中B3LYP/6-311+G(3df，2p)密度泛函方法进行计算。计算是在孤立分子上进行的，没有使用周期性边界条件。对全氟正戊烷分子进行计算时的输入文件和说明如下所示。主要定义了计算的内存、核数、节点数以及chk文件的存储路径；计算使用关键词opt和freq，其中opt表示对相应的分子进行结构优化，freq指对分子进行频率分析；本案例的作业名称FC-87；全氟正戊烷分子的电荷数和自旋多重度以及元素类型和坐标。对分子几何结构进行优化，使其收敛到最小能量状态。当计算结束后，将获得输出文件FC-87.out。

%chk=FC-87.chk //checkpoint 文件

%mem=20GB //内存设置

%NPROC=24 //并行CPU数

#b3lyp/6-311+G(3df，2p)opt freq //计算执行路径行

//空白行

FC-87 //标题行

//空白行

0 1 //电荷与多重度

C -1.36939919 2.12865942 4.88066734

C-0.69162716 2.91905593 3.74598747

C-1.02042488 2.2597723 2.39364241

C-0.50193211 0.80968554 2.38994949

C-0.83072983 0.15040191 1.03760443

F-1.14615004 4.19023589 3.74922477

F-1.08116742 2.70660287 6.06616463

F-0.91487631 0.85747947 4.87743004

F0.6452783 2.91869949 3.93356055

F-0.42627407 2.95265236 1.39895551

F0.83497335 0.80932909 2.57752257

F-1.09608292 0.11680548 3.38463639

F-0.23657902 0.84328197 0.04291753

F-0.37620695 -1.12077805 1.03436713

F-2.35733034 2.26012875 2.20606933

F-2.16763529 0.15075835 0.85003135

F-2.70630465 2.12901587 4.69309426 //分子结构

(3)极化率计算。通过GaussView打开FC-87.out文件，选择能量最低结构，保存分子模型文件为FC-87_polar.cif。对优化后的全氟正戊烷分子再次计算时的输入文件和说明如下所示，关于极化率计算的原理及详细公式可以参阅Multiwfn说明书[23]。计算使用关键词polar以得到极化率。当计算结束后，将获得输出文件FC-87_polar.out。

%chk=FC-87_polar.chk //checkpoint 文件

%mem=20GB //内存设置

%NPROC=24 //并行CPU数

#b3lyp/6-311+G(3df，2p)polar //计算执行路径行

//空白行

FC-87_polar //标题行

//空白行

0 1 //电荷与多重度

C 2.25775100 -0.61584400 0.11472800

C1.43220700 .65673800 -0.25428400

C-0.06062500 0.73860600 0.23773400

C-1.01350400 -0.43003900 -0.17370500

C-2.53700700 -0.13177400 0.03113600

F2.05817000 1.71187100 0.29997800

F3.53166100 -0.40634000 -0.21015800

F1.81641600 -1.67518600 -0.56137500

F1.46119700 0.79338300 -1.58955200

F-0.54949300 1.88750100 -0.27027000

F-0.83367200 -0.72779000 -1.47242800

F-0.70913100 -1.50844000 0.57064200

F-2.96618500 0.77734500 -0.83854800

F-3.21661100 -1.26102200 -0.16447800

F-0.05540400 0.83070200 1.57759800

F-2.77208200 0.30158600 1.26857500

F2.18258600 -0.86873500 1.41961100 //分子结构

(4)Multiwfn解析polar输出。Gaussian的许多输出信息难以直接分析，Multiwfn程序可以解析polar关键词产生的(超)极化率，使输出结果简洁易懂。我们使用的为Multiwfn 3.8版本，首先输入Gaussian的polar计算任务的输出文件的路径，例如：C： FC-87_polar.out，进入主功能200，输入7，解析Gaussian的(超)极化率的计算输出。由于我们使用的是B3LYP杂化密度泛函，故这里在界面里选择1 "Polar"+analytic 3-order deriv. (HF/DFT/Semi-empirical)，输出结果如下所示，极化率体积由各项同性平均极化率体积来表示。

Static firsthyperpolarizability：

XXX=10.21520

XXY=1.42486

XYY=-3.82634

YYY=2.33057

XXZ=-3.17366

XYZ=0.82783

YYZ=-2.41357

XZZ=-0.38349

YZZ=1.25583

ZZZ=2.77196

Beta_X=6.00537 Beta_Y=5.01126 Beta_Z=-2.81527

Magnitude of firsthyperpolarizability：8.31282

Projection of beta on dipole moment：-7.45932

Beta ||：-4.47559

Beta ||(z)：-1.68916

Beta _|_(z)：-0.56305

图1 介电常数计算流程图

3 结构分析与讨论

我们一共选择了5种氟化物进行研究，FC-87，FC-72，FC-3283，FC-43和PF-3284均为良好的制冷剂材料，并且已经实现商业化。优化后的分子结构式如图2所示。表2给出了分子的名称以及必要的物理和化学性质。

图2 5种制冷剂分子的优化结构

表2 制冷剂对应的分子名称，密度及摩尔质量

表3中报告了5种物质的实验介电常数以及根据DFT计算的极化率体积和实验密度计算得出的介电常数。随后将这些计算值与实验值进行比较，实验值由浙江化工研究院有限公司提供。5个分子的介电常数计算值均小于实验值，相对误差在10.4%到14.0%，平均误差为12.0%。

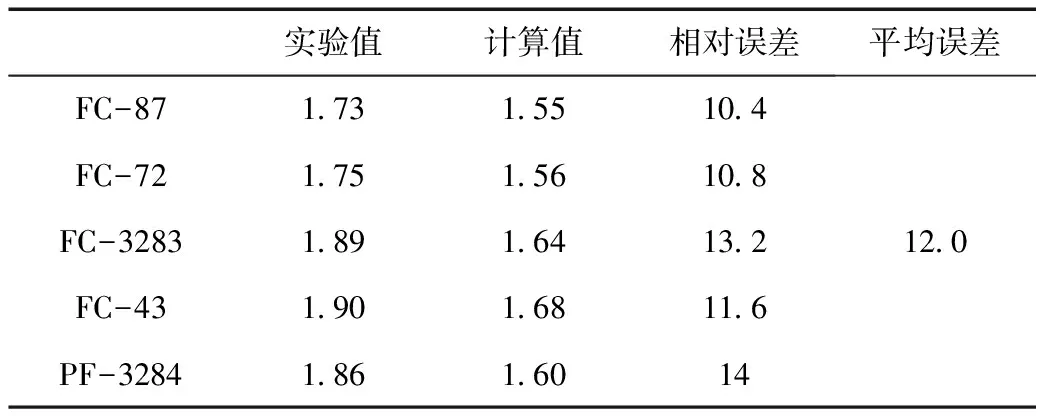
表3 制冷剂介电常数的实验值，计算值与误差

图3进一步显示了使用B3LYP/6-311+G(3df，2p)研究的每个分子的实验值和计算值的比较。普遍意义上，这种方法稍稍低估了介电常数的真实值，但仍然能够给出相应的介电常数的相对趋势，足够在物理化学教学实验中通过量子化学的模拟手段来预测制冷剂材料的介电常数值。

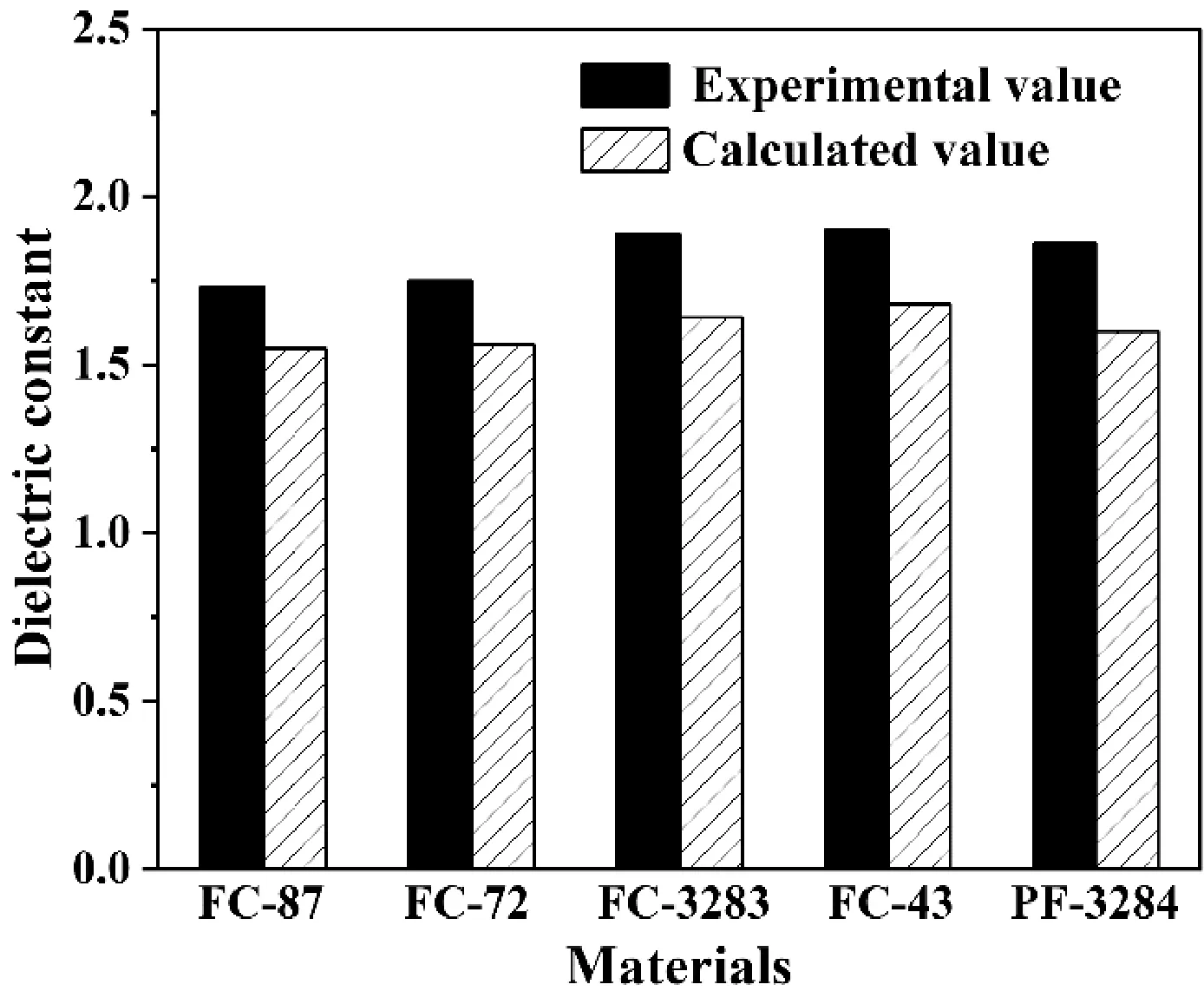
图3 介电常数计算值与实验值的比较

4 结 语

本文利用量子化学计算预测制冷剂材料的介电常数。计算方法具有准确性、相对快速性和易于执行的优点。一方面可以免去做实验所需要的设备，以及回避了某些药品的限制，另外一方面可以增加学生对介电常数相关物理化学内涵的理解，提高化学教学课堂的生动性，能够更加合理的分配教学时间，将物理化学学课内容与量子计算手段有效结合，帮助同学们加深介电常数其物理化学含义的理解。