基于有效降雨量的滑坡位移-降雨相关性研究
朱智杰,卢书强,梅 军
(1.三峡大学 湖北长江三峡滑坡国家野外科学观测研究站,湖北 宜昌 443002; 2.三峡大学 土木与建筑学院,湖北 宜昌 443002)
0 引 言
降雨型滑坡的发生通常与临界降雨量有关,若超过此雨量界限,可能会发生滑坡[1-2]。临界降雨量可以根据物理参数或统计分析来定义,并可用于滑坡预警模型研究[3-4]。还可根据降雨的短期效应与瞬时降雨事件相关的参数来确定临界降雨量[5],这表示降雨事件与位移事件存在一定统计学规律,因此,可采用统计学方法分析位移与降雨量的相关性,得到诱发滑坡发生的降雨阈值曲线及临界降雨量[6],进而计算出发生降雨诱发滑坡的概率[7]。
国内外学者对滑坡位移与降雨进行相关性分析,取得了显著成果。例如对土质滑坡坡体位移与降雨量关系曲线进行非线性回归分析,得出降雨量与位移关系服从幂函数分布[8];利用偏相关系数表示滑坡位移次数与降雨量的相关度以及相关系数表示滑坡位移次数与降雨强度的相关度[9];用Logistic回归方法对位移-降雨量数据集进行拟合,得到不同的概率阈值,再通过ROC特征分析确定最佳阈值[10]。
虽然上述成果都探究了位移-降雨之间的相关性。但在降雨过程中,并非所有降雨量都对滑坡变形产生作用[11]。因此,降雨事件中的有效降雨量,对于降雨型滑坡预测预报非常重要,这使有效降雨量相对于日降雨量在滑坡变形分析中更具有实际意义[12]。
结合上述理论及前人研究,本文以“多次连续降雨构成的有效降雨量组成”为模型基础,再利用Pearson方法,对滑坡降雨量和位移量进行相关性分析,建立在不同衰减系数下相关系数和位移的Logistic回归模型。得到滑坡进入加速破坏状态时衰减系数的最佳取值,并通过调整判定系数和残差平方和等参数对模型进行评价。对降雨诱发型滑坡有效降雨量计算中的衰减系数取值问题提供一种新的研究思路。
1 降雨量模型简介
1.1 日降雨量模型
这种降雨量模型需要对诱发滑坡变形发生的降雨量通过简单计算或统计,确定区域群发滑坡或者单体滑坡发生之日的临界降雨量,从而进行滑坡灾害预警。它只需考虑单日的降雨量数据,通过累加小时降雨量计算日降雨量的上下限[13]。日降雨量模型可以用式(1)表示。
(1)
式中:R0为日降雨量(mm);RH为1 d中第H小时降雨量(mm);H为经过的小时(h)。
1.2 前期降雨量模型
前期降雨量模型用来统计滑坡发生位移之前的降雨量,通过简单累加关系,计算出滑坡发生位移前期一定时间段内日降雨量的累计值,在一次滑坡事件中,前期降雨量可以作为滑坡预警阈值的参考[14]。即达到统计得出的滑坡阈值前期降雨量,就有一定概率诱发滑坡事件发生[15]。前期降雨量模型可以用式(2)表示。
(2)
式中:RL为前期降雨量(mm);Ri为第i日降雨量(mm);n为经过的天数(d)。
1.3 有效降雨量模型
为了更好地反映日降雨量和前期降雨量对地质灾害的作用,需要考虑前期降雨量的衰减作用。定义在衰减周期内第1次降雨至滑坡开始变形的时间区间为“一次降雨有效作用期”,在此基础上,引入“多次连续降雨构成的有效降雨量构成”[16],如图1所示。

图1 多次连续降雨构成的有效降雨量构成
如图1所示的“有效降雨量”即为经过衰减作用计算得到的前期降雨量+滑坡发生变形当日降雨量[17],有效降雨量模型可以用式(3)表示。
(3)
式中:Rc为对滑坡变形发生起作用的有效降雨量(mm);R0为滑坡事件日的降雨量;αi为衰减系数。
由于滑坡在不同降雨时间间隔内,衰减系数取值存在一定差异。因此,在考虑时间间隔对衰减系数的影响作用下,参考区域降雨型滑坡衰减系数取值公式,笔者采用式(4)计算滑坡有效降雨量模型中的衰减系数αi。
(4)
式中t为前次降雨距离当次降雨的时间(d)。
2 小岩头滑坡变形特征
2.1 小岩头滑坡概况
该滑坡前缘高程300 m,后缘高程360 m,滑坡体纵长约120 m,横宽70~80 m,面积约9 000 m2,滑坡体厚度5~15 m,体积约9×104m3。本次滑移区范围纵长约100 m,横宽约40 m,体积约4×104m3;滑移牵引区位于滑移区两侧及后缘,体积约5×104m3。滑坡全貌如图2所示。
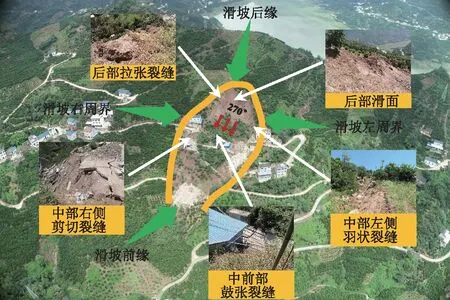
图2 小岩头滑坡全貌
在滑坡体中后缘及两侧边界上安置监测设备,构成一纵一横纵剖面(Ⅰ-Ⅰ’)与滑坡主滑方向一致,布置于滑坡体中轴线位置和滑坡左、右侧边界位置,横剖面与横穿该滑坡的公路大致平行[18]。在该滑坡上共布设4个裂缝自动监测仪器,各裂缝监测点布置平面图见图3(a)。
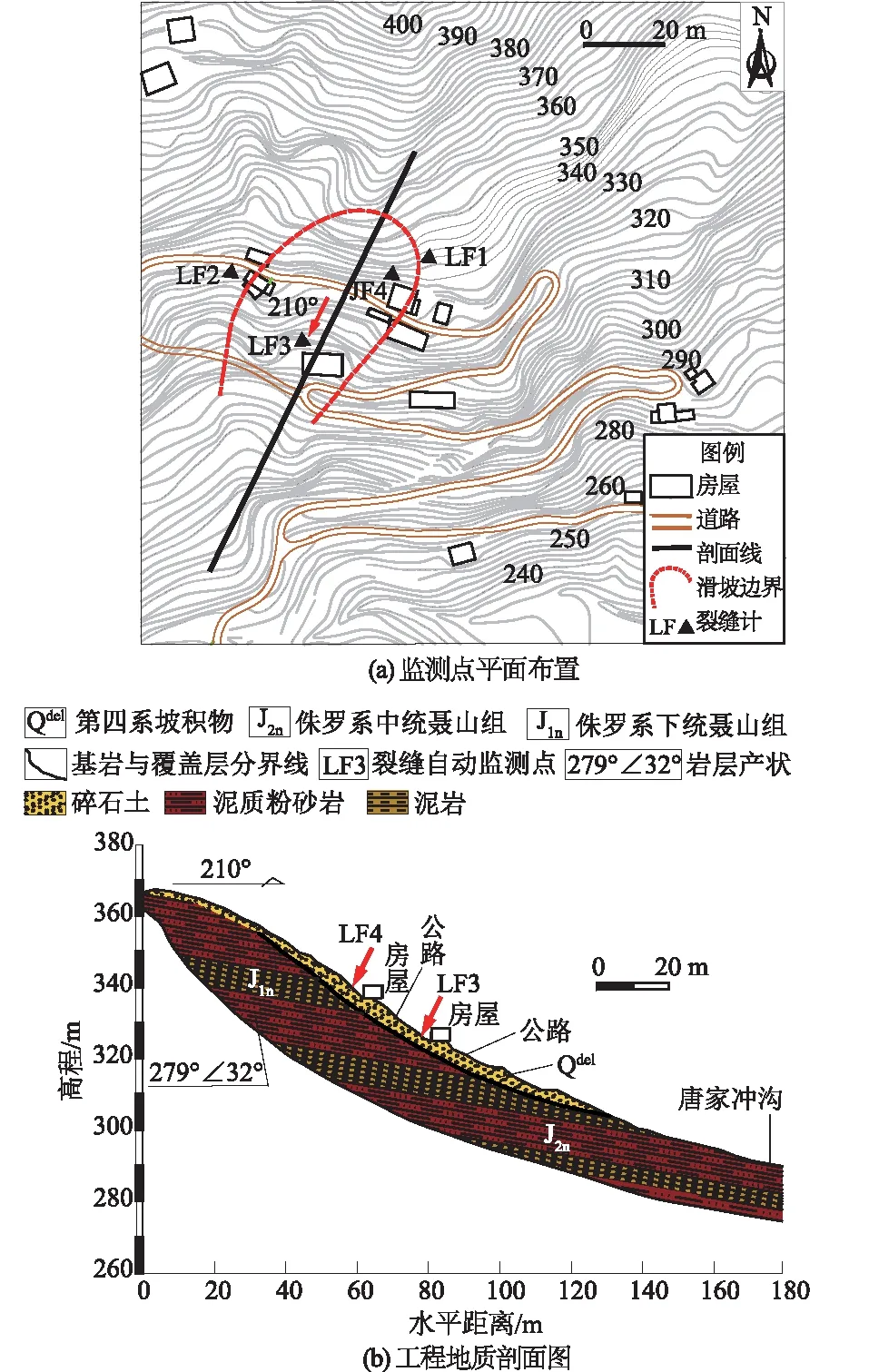
图3 监测点平面布置及工程地质剖面图
滑坡表面上覆土层为紫红色夹灰黄色残坡积黏土夹碎石土,成分为泥岩、粉砂岩,厚度不均,一般厚1~3 m。下伏地层为侏罗系中、下统聂家山组(J1-2n)紫红色泥质粉砂岩夹灰绿色泥岩等,岩层产状279°∠32°,坡体结构类型为斜向坡。小岩头滑坡的工程地质剖面图见图3(b)。
2.2 滑坡监测数据分析
由于小岩头滑坡LF2监测点位移变化不明显,LF1、LF3和LF4在2021年8月发生同步变形,故主要选取在滑坡变形较大时间段内产生位移的LF1和LF4的裂缝计监测位移数据,统计分析结果如表1。

表1 小岩头滑坡诱发“阶跃”特征统计
地表裂缝位移-降雨量-时间曲线分别在2020年10月、2021年7月和2021年8月呈现3个变形加速期,第1个跃升期为LF1监测点在连续3 d高雨强作用下的变形加剧,第2个跃升期为LF4监测点在连续6 d低雨强作用下的变形加剧,第3个跃升期为LF1监测点在连续2 d高雨强作用下的变形加剧,直至滑坡滑动。
把监测点裂缝位移曲线划分如下: A(2020年10月3—11日)为第1次“激发阶跃”阶段、B(2021年7月8—25日) 为第2次“激发阶跃”阶段、C(2021年8月26—28日) 为第3次“加速破坏”阶段[19]。
根据监测数据的分析结果,可以发现小岩头滑坡3个“阶跃”阶段的前次降雨与滑坡发生位移日的降雨有效作用期t都没有超过 7 d,即当有效作用期超过 7 d时,可以认为超过部分的降雨对滑坡位移的影响近似忽略不计[20]。在这种情况下,笔者取前次降雨最大有效作用期为 7 d。
2.2.1 第1次“激发阶跃”阶段
由图4(a)可知,2020年10月4日降雨后 7 d,LF1的变形才基本停止,此次为连续3天的集中降雨过程。降雨模式为前期降雨+当日降雨,确定降雨有效作用期t为3 d,变形阶段最大位移速率为12.62 mm/d,为典型的“多次连续降雨构成的有效降雨构成”,由式(1)、式(2)计算得当日降雨量为52.3 mm,前期降雨量为57.6 mm,根据式(3)计算得到在当前降雨模式下有效降雨量为109.9 mm[21]。

图4 LF1、LF4位移数据-降雨量曲线
2.2.2 第2次“激发阶跃”阶段
由图4(b)可知,2021年7月8日降雨后,滑坡变形至2021年7月15日才逐渐停止,2021年7月8日之前的降雨由5次不连续降雨组成。降雨模式以当次降雨为主,确定降雨有效作用期t为5 d,变形阶段最大位移速率为1.49 mm/d,为典型的“多次连续降雨构成的有效降雨构成”,由式(1)、式(2)计算得到日降雨量为34.8 mm,前期降雨量为72 mm,根据式(3)计算得到在当前降雨模式下有效降雨量为106.8 mm。
2.2.3 第3次“加速破坏”阶段
由图4(c)可知,2021年8月26日降雨后,滑坡变形速率开始急剧增大,至2021年8月28日整体滑动前1 d最大位移速率为2.31 mm/d,降雨模式为前期降雨+当次降雨,确定降雨有效作用期t为 2 d,根据“多次连续降雨构成的有效降雨构成”,由式(1)、式(2)计算得到当日降雨量为51.8 mm,前期降雨量为65.1 mm,根据式(3)计算得到在当前降雨模式下有效降雨量为116.9 mm。
3 位移-降雨关系研究
3.1 位移-降雨相关性
降雨时间相对集中、降雨强度大及降雨量多都是典型降雨诱发滑坡所具有的特点。这些特点表明无论是降雨时间、降雨强度还是降雨量,都与降雨型滑坡位移频次之间存在一种正向关系,这证明了滑坡位移与其变形前降雨相存在一定相关性,为进一步定量研究滑坡位移与降雨之间相关关系奠定了基础[22]。
采用Pearson相关系数公式分别计算累计位移与日降雨量相关系数r0、累计位移与前期降雨量之间的相关系数rl、累计位移与有效降雨量之间的相关系数rc,计算公式如(5)。
(5)
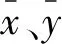
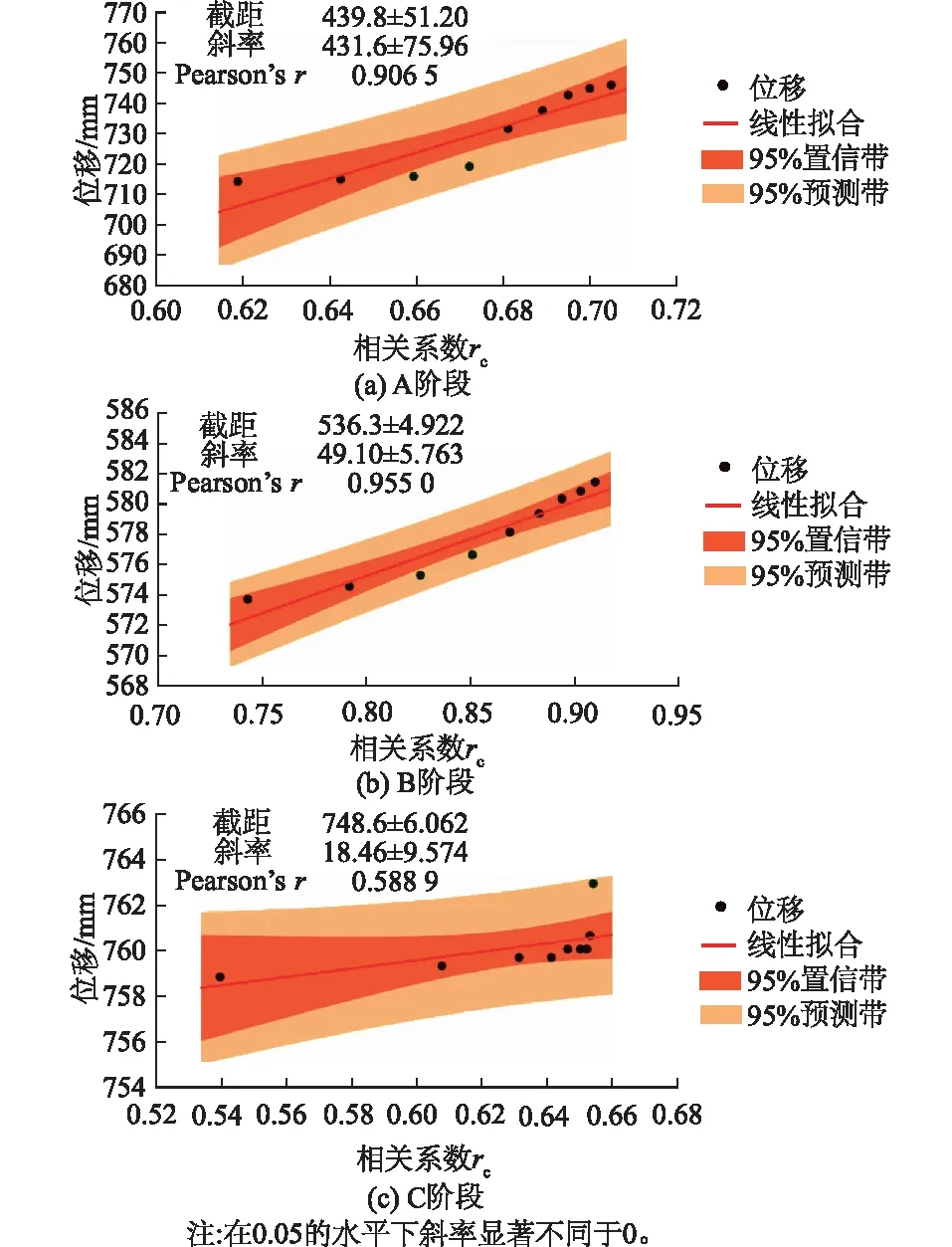
当r<0.2时,x、y相关度极弱,可视为不相关;当0.2≤r≤0.4时,x、y为弱相关;当0.4 3.1.1 位移-日降雨量 由式(1)分别计算得到A、B、C 3个阶段的日降雨量,对累计位移和日降雨量进行描述统计和Pearson相关系数计算,数据取变形前7 d+变形持续时间9 d,个案数共计16,其中累计位移平均值为722.786 mm,日降雨量平均值为8.619 mm,标准偏差分别为13.494和18.369,雨量时空分布不均匀,为雨强集中型降雨[24]。相关性系数r0按阶段划分所得结果如表2所示。 表2 位移-日降雨量相关性 A阶段两者的Pearson相关系数为-0.310,B阶段Pearson相关系数为-0.376,C阶段Pearson相关系数为-0.243。相关系数均为负值,证明累计位移和日降雨量呈负相关,且此类相关系数分布于0.2和0.4之间,可知两者相关度低,为弱相关。 3.1.2 位移-前期降雨量 由式(2)分别计算得到A、B、C3个阶段的前期降雨量,数据取变形前7 d+变形持续时间18 d,个案数共计25,其中累计位移平均值为578.845 mm,日降雨量平均值为6.392 mm,标准偏差分别为4.356和10.608,降雨分布较均匀且雨强分散。相关性系数rl按阶段划分所得结果如表3所示。 表3 位移-前期降雨量相关性 A阶段两者的Pearson相关系数为0.7,B阶段Pearson相关系数0.895,C阶段Pearson相关系数0.631。相关系数均为正值,证明累计位移量和前期降雨量呈正相关,且此类相关系数分布于0.6和0.9之间,可知两者相关度高,为强相关-极强相关。 3.1.3 位移-有效降雨量 在滑坡变形开始后,降雨渗流逐渐沿地表裂缝等入渗途径下渗,致使入渗过程中的土体颗粒由不饱和状态变为相对饱和状态[25],此时的衰减系数取值相对于式(4)中的衰减系数必然有所不同。 因此,为研究滑坡变形过程中有效降雨量计算的衰减系数取值问题,笔者取αi=0.1,0.2,…,0.9,由式(3)、式(4)求出小岩头滑坡在每个“阶跃”时间段内有效降雨量。数据选取变形前7 d+变形持续时间3 d,个案数共计10。在衰减系数不同的情况下,得到滑坡位移和有效降雨量的相关系数rc见表4。各变形阶段相关性系数与位移关系如图5所示。 表4 不同衰减系数下位移-有效降雨量相关性 图5 不同衰减系数下相关系数与位移的关系 如图5所示,A、B、C 3个时间段有效降雨量都远大于累计降雨量与日降雨量,通过有效降雨量模型计算得出的相关系数远高于由日降雨量计算的相关系数。裂缝位移与日降雨量并没有很强的关联性,由日降雨量直接计算出的相关系数都呈负值。各阶段位移与前期降雨量相关系数分别为0.700、0.895、0.631,位移与有效降雨量最大相关系数分别为0.705、0.910、0.656,相比之下,有效降雨量与位移的相关程度最高。 当衰减系数αi取0.4时,位移-降雨相关系数取值位于A阶段位移-有效降雨量“斜率最大拐点”,有效降雨量与LF1位移的相关系数为0.672,表明该时间段有效降雨量与滑坡位移呈现出强相关性;当衰减系数αi取0.4时,位移-降雨相关系数取值位于B阶段“斜率最大拐点”,有效降雨量与LF4位移的相关系数为0.851,证明该时间段有效降雨量与滑坡位移为强相关;当衰减系数αi取0.7时,位移-降雨相关系数取值位于C阶段“斜率最大拐点”,有效降雨量与LF1位移的相关系数为0.654,即有效降雨量与滑坡位移表现强相关性。 从相关性的总体变化趋势上看,A、B、C阶段位移和降雨的相关系数r都随降雨衰减系数αi的增大而增大。说明衰减系数取值越大,滑坡位移和降雨的相关性越强。当相关系数-位移曲线斜率越大时,位移随衰减系数增减而产生的变化就越明显,表明衰减系数的取值越准确。 A、B阶段滑坡均未产生大规模滑动,但C阶段中,相关系数在“斜率最大拐点”处产生突变,而此时的相关系数却小于A、B阶段,随后滑坡整体滑动破坏。由此,根据衰减系数和相关系数的变化可判定滑坡是否进入加速变形破坏阶段。 为进一步研究不同衰减系数αi下相关系数和位移的内在联系,笔者对数据集进行线性回归以求得拟合模型,并使用Anderson-Darling统计量对残差进行正态检验。运用线性逻辑回归方程如式(6)所示[26]。 y=β0+β1x+ε。 (6) 式中:β0、β1为回归参数;x为自变量;y为因变量;ε为误差项。 用带残差的Logistic回归模型对数据集进行拟合得到回归方程如表5,拟合曲线如图6。 表5 回归方程 图6 各阶段拟合曲线 通过线性回归方程得到R2(调整判定系数)、SSR(回归平方和)和SSE(残差平方和)。拟合优度检验成果如表6,方差分析如表7。分析后可知: 表6 拟合优度检验 表7 方差分析 (1)A阶段R2=0.822,SSR=1 255.382,SSE=272.159,P=7.489×10-4<0.05,在0.05置信水平下,变量间具有强相关性且回归方程显著。 (2)B阶段R2=0.912,SSR=60.588,SSE=5.844,P=6.09×10-5<0.05,在0.05置信水平下,变量间具有极强相关性且回归方程显著。 (3)C阶段R2=0.347,SSR=3.870,SSE=7.288,P=0.095>0.05,在0.05置信水平下,数据相关性弱且不具有正态分布特征。 综上,A、B阶段的置信区间和预期区间相对较窄,说明这两个阶段的模型解释能力最好,自变量对因变量的解释度越高,回归方程的拟合优度越大,此时衰减系数αi取值为0.4,滑坡处于匀速变形阶段。C阶段的回归方程不显著,位移-有效雨量数据相关性差,此时的衰减系数αi取0.7时,滑坡处于加速变形破坏阶段[27]。 (1)小岩头滑坡在3个“阶跃”时间段内,降雨模式为“前期降雨+当日降雨”,有效降雨量分别为109.9、106.8、116.9 mm。即有效降雨量>116.9 mm时,滑坡“阶跃”现象出现。降雨停止后,滑坡变形在 7 d之内恢复正常,可以确定小岩头滑坡的降雨时间间隔阈值为 7 d。 (2)在小岩头滑坡变形前的每个“阶跃”阶段,可以通过Pearson方法简单分析滑坡位移序列-降雨序列的相关性,再利用每个阶段所建立的位移-降雨线性回归模型,可得出此阶段的相关系数。最后通过参照不同衰减系数下有效降雨量-位移相关性表,获取此阶段的衰减系数αi,进而可求得每个“阶跃”阶段有效降雨量Rc,可使雨量监测预警模型的精确度提高。 (3)小岩头滑坡A、B、C阶段位移和降雨的相关系数r都随降雨衰减系数αi取值的增加而增加。当相关性系数处于“斜率最大拐点”时,位移随衰减系数增减而产生的变化就越明显,表明衰减系数的取值越准确。当位移-降雨数据相关系数突然变小,衰减系数突然增大时,可判定滑坡进入加速破坏变形阶段。 (4)不同区域内的滑坡,降雨衰减系数不尽相同。同一滑坡,选取不同变形时间段,滑坡体的降雨入渗系数也不同,衰减系数也有较大差异,此类滑坡在有效降雨量计算过程中的衰减系数取值问题有待深入探讨。



3.2 位移-相关系数回归模型
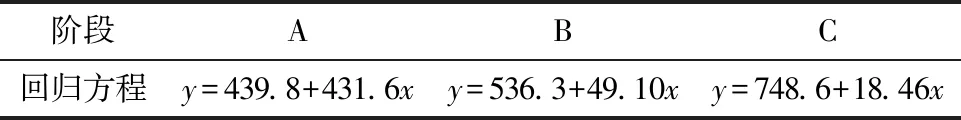


4 结 论

