一种改进的随机向量函数链接网络集成模型

季洋洋, 王士同

(江南大学人工智能与计算机学院, 江苏 无锡 214122)

神经网络训练通常采用反向传播算法(back propagation, BP), 易出现陷入局部最小值、对学习率敏感以及收敛速度较慢等问题．为了解决这些问题, 随机向量函数链接网络[1](random vector functional link network, RVFLN)应运而生．RVFLN是一种单层前馈神经网络, 其隐藏神经元参数(输入权重和偏置)是在一个合适的区间内随机生成, 而输出权重则是通过简单的闭式解得出．RVFLN通过特征复用或直接链接将原始数据传到输出层, 修正正则化参数, 故比其他同类网络更加轻量化和简单化．

传统RVFLN中的直接链接仅作简单线性变换, 即使存在随机权重,单个RVFLN之间的多样性差异也很小．而神经网络为不稳定算法, 训练过程中包含多个随机化操作, 即使随机种子变化很小, 其性能差异也可能较大, 从而形成了单个神经网络之间的多样性．通过使用不同的超参数和直接链接模型, 再利用相对投票法、加权投票法和学习法进行集成, 可有效降低错误率．

集成学习通常分为同质集成和异质集成, 每个基分类器之间具有一定的差异性．常见的集成算法有Bagging、 Boosting以及Stacking等, 在实际应用中备受关注．Yu等[2]使用Bagging算法集成RVFLN, 完成石油价格的预测; Zhang等[3]利用Boosting加速集成RVFLN, 建立温度预测模型; Tahir等[4]提出了一种Stacking集成RVFLN的新型算法, 用于多通道跌落检测．上述方法可在一定程度上提升RVFLN的预测能力, 但由于神经网络中直接链接逆矩阵的计算复杂, 随机权重的简单初始化使得各神经网络之间的差异性较小, 导致RVFLN的训练速度和集成多样性有限, 进而影响模型的泛化能力及预测精度．针对以上问题,本文拟提出一种以改进随机向量函数链接网络为基分类器的集成模型,采用6种简单回归替换传统RVFLN中计算复杂的直接链接, 并利用高斯过程回归(Gaussian process regression, GPR)方法初始化隐含层参数, 优化隐含层随机权重, 增加单个基学习器之间的多样性, 最终集成6个具有差异性的基分类器得到预测模型, 旨在提高预测精度的同时增强模型的鲁棒性和泛化能力．

1 随机向量函数链接网络

RVFLN的基本网络结构如图1所示．RVFLN中输出层由隐藏层的非线性变换H和原始输入特征X组成．由于隐藏层参数μk和σk是随机生成并在训练过程中保持不变, 因此仅计算输出权重矩阵βk, 其优化问题可表示为arg min(‖Dβk-Y‖2+λ‖βk‖2),其中D为隐藏特征和原始特征的级联矩阵,D=[HX];λ为正则化参数;Y为标签矩阵．通常采用Moore-Penrose伪逆(λ=0)或岭回归(λ≠0)的闭式解求得输出权重．Moore-Penrose伪逆方法中,βk=D†Y; 使用正则化的最小二乘法(即岭回归)时, 原始空间βk=(DTD+λI)-1DTY, 对偶空间βk=DT(DDT+λI)-1Y, 其中I为单位矩阵．

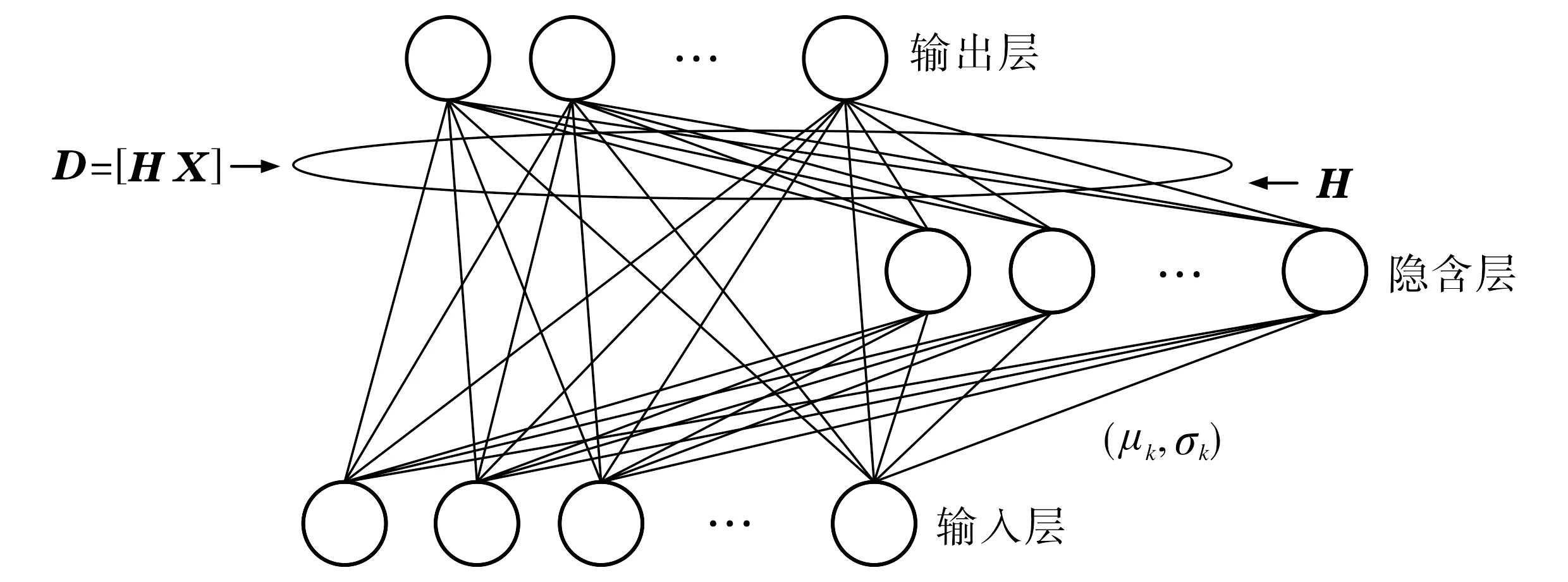
图1 RVFLN网络架构

2 改进的随机向量函数链接网络

2.1 简单回归模型

假设数据集(yi,xi),i=1,2,…,n, 其中xi=(xi1,…,xip)是p维的预测变量,yi是对第i个观察值的响应．回归模型f对输入向量x进行预测,得到预测值

(1)

本文采用简单回归模型

(2)

替换传统RVFLN中的直接链接, 其中αj为启发式选择权重, 独立于位置参数β0和比例参数γ．预测变量的组合或选择取决于加权和, 参数β0和γ分别确定了加权和的位置和尺度．

2.1.1 平均预测模型

平均预测模型是最简单的线性模型, 常用于预测训练集响应变量的平均值．模型预测公式为

(3)

此模型通常用于无法取得响应变量的数据集, 并不适合监督学习, 但仍可作为一个基准．

2.1.2 随机权重模型

当数据进行标准化和定向后, 每个预测变量会与一个随机权重相乘, 该随机权重从某一均匀分布的数据中取得．模型可表示为

(4)

其中输入向量权重ωj～u(a,b),a和b的取值不固定, 本文令a=0,b=1．

2.1.3 等权模型

等权模型将所有标准化预测标量进行同等加权, 即

(5)

在所有预测变量都是有向的假设下, 等权模型只有位置和尺度两个自由参数．

2.1.4 关联权重模型

关联权重模型通过计算预测变量和响应变量的相关性,对所有预测变量进行加权, 即

(6)

其中ryxj为预测变量xj与响应变量y之间的关联系数, 关联权重须估计p+2个参数．

2.1.5 单线索回归模型

单线索回归模型仅考虑与所有预测变量拥有最高相关性的预测变量．模型表达式为

(7)

其中x1为与响应变量y具有最高关联度的预测变量, 计算所有预测变量和响应变量之间的相关性, 取最大绝对值．

2.1.6 关联等级排名模型

关联等级排名模型无须确定关联程度的确切值, 只计算等级排名, 即相对顺序．模型公式为

(8)

其中ρj=rank(ryxj)．预测变量中, 关联程度最低的等级为1, 最高等级为p, 相同关联性使用平均排名, 例如向量(7,4,4,2)的等级排名为(4,2.5,2.5,1)．关联程度排名比关联权重更易于估计, 且鲁棒性更强．

2.2 GPR方法

为保证投影后的信息损失最小, 采用GPR方法[5]初始化隐含层参数．隐含层权重

(9)

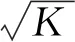
2.3 集成策略

传统RVFLN表达式可改写为

(10)

其中参数βk通过训练集的训练得出,

βk=H†Y,

(11)

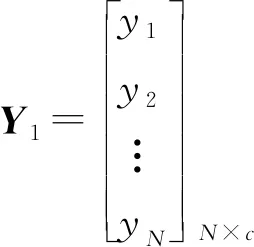
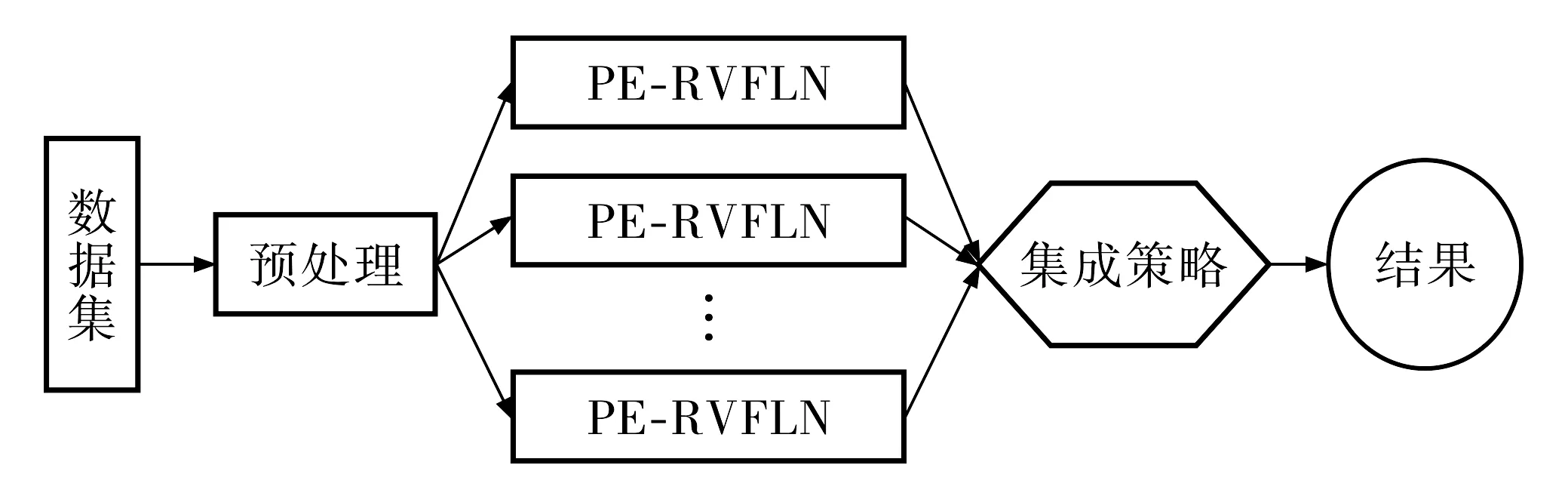
图2 集成PE-RVFLN

在改进的随机向量函数链接网络PE-RVFLN中, GPR方法的时间复杂度为O(N), 隐含层输出的复杂度为O(Nzn), 其中n为隐含层节点数量,z为属性数量, 最后利用伪逆矩阵计算出参数βk的复杂度O(z3)．

3 实验结果与分析

3.1 数据集

选取UCI和KEEL数据库[8]中16个不同领域的数据集进行测试实验, 所选数据集的基本信息如表1所示, 其涵盖了大、中、小规模的二分类以及多分类任务．实验硬件环境为AMD Ryzen 9 5900HX@ 3.3 GHz, 运行内存为16 GB, 集成开发环境为PyCharm 2021.2.4．

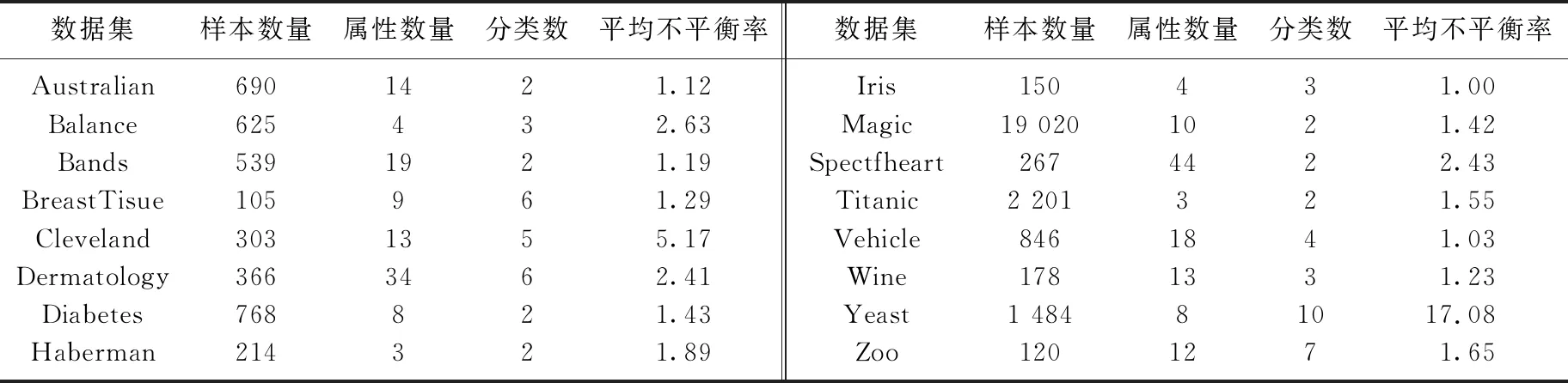
表1 数据集基本信息

3.2 实验设计

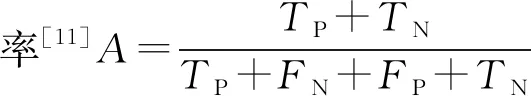
3.3 结果分析

表2为集成随机向量函数链接网络与其他5种算法在16个数据集上的准确率和标准差．由表2可知, 本文所提集成模型的准确率比基分类器BaseClassifier高4.80%,比传统算法SVM高4.17%, 比集成模型RandomForest和Bagging分别高2.46%和2.60%,比传统RVFLN高1.73%; PE-RVFLN的标准差比基分类器BaseClassifier低3.97%,比传统算法SVM低22.91%,比集成模型RandomForest和Bagging分别低23.06%和20.86%,比传统RVFLN低11.24%．综上得出,改进的随机向量函数链接网络具有明显优势, 较传统集成算法和RVFLN的精确度和稳定性均有所提升,同时具有良好的泛化性能．

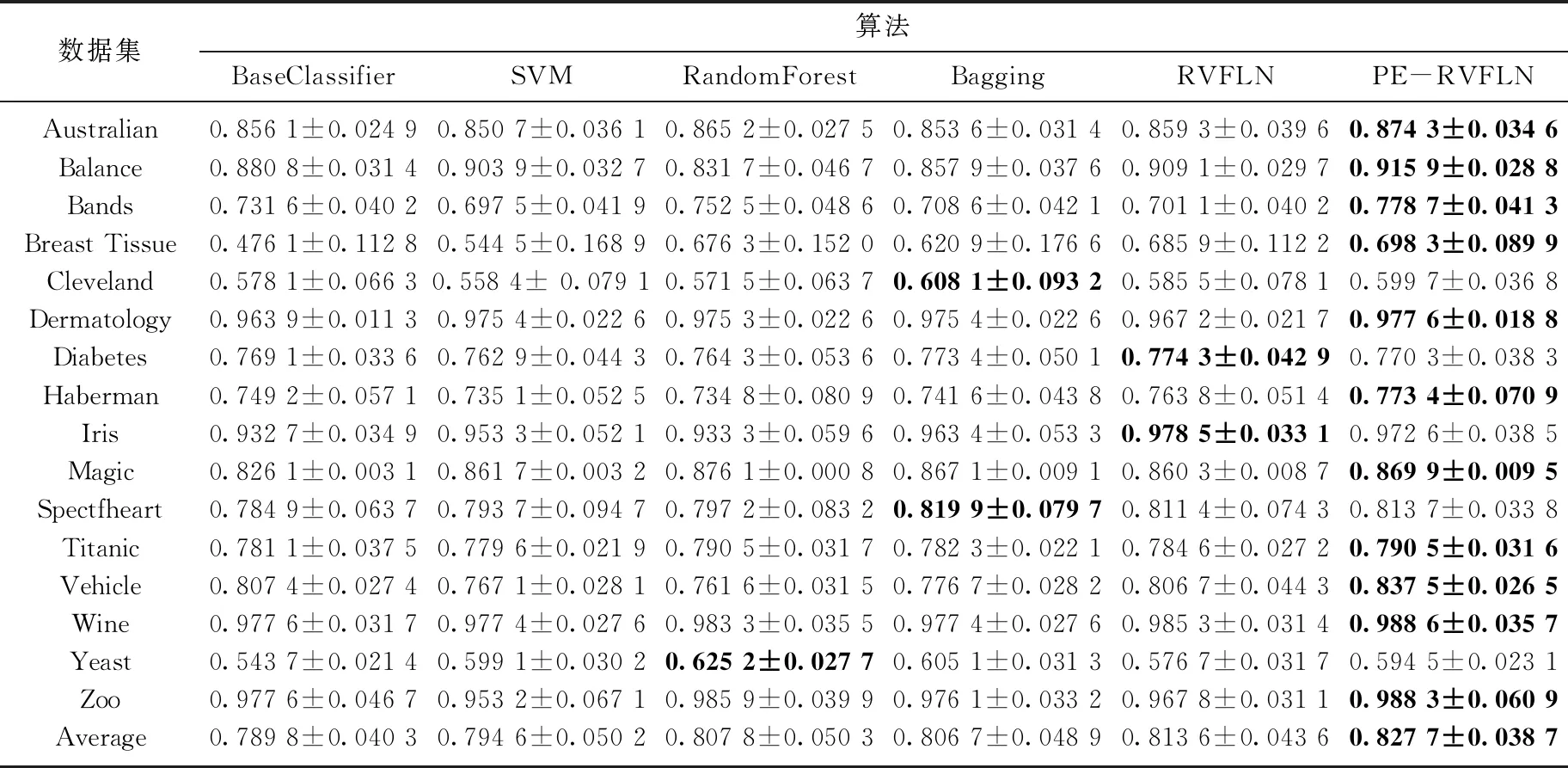
表2 各算法在不同数据集上的准确率和标准差

4 结论

本文提出了一种改进的随机向量函数链接网络集成模型,采用6种不同的简单回归模型代替传统随机向量函数链接网络的直接链接,优化隐含层的随机权重取值, 并使用正则项降低信息损失．实验表明改进的集成模型能够显著提升预测精度,且具有良好的泛化能力和鲁棒性,既保证了基分类器的多样性,又提升了集成学习的效果．