一种改进启发函数的A*算法

樊康生, 杨光永, 黄训爱, 陈旭东, 徐天奇

(云南民族大学电气信息工程学院, 昆明 650500)

路径规划是轮式移动机器人领域的研究重点[1]. 根据已知环境信息可将路径规划分为局部规划和全局规划, 全局路径规划算法主要有Dijkstra算法[2]和A*算法[3-4]等, 其中A*算法因其规划路径短和计算速度快而得到普遍应用. 然而, 传统A*算法存在规划路径搜索节点多和转折角度大等缺点[5], 故为了提升A*算法的性能, 诸多学者提出了改进方法．赵晓等[6]使用跳点搜索策略, 加快了搜索速度, 但优化后的路径存在大角度的拐点; Tang等[7]将几何思想引入算法中,缩短了路径长度, 但增加了搜索时间; Shang等[8]通过删除边生成更短的k倍路径, 提高了搜索效率, 但增加了寻路时间; Mi等[9]基于快速搜索随机树(rapidly-exploring random tree, RRT)和跳点搜索(jump point search, JPS)改进A*算法, 有效减少了无用扩展节点, 提高了搜索效率和路径平滑度, 但增加了路径长度; Zhang等[10]提出了一种包含双向扇区扩展和变步长搜索策略的改进A*算法, 提高了搜索效率,但路径较长; Zhang等[11]采用混合蚁群算法改进A*算法, 提高了规划路径的安全性,但搜索效率较低; Sui等[12]利用粒子群算法改进A*算法, 获得较短的优化路径,但算法复杂度较高且不稳定; Dong等[13]提出几何A*算法, 有效缩短了规划路径,但搜索效率较低; Sang等[14]采用混合人工智能改进A*算法, 有效提高了算法搜索效率,但路径转折拐点较多; Liu[15]和Lai[16]等利用Bézier曲线获得了较为平滑的路径, 但增加了路径长度; Zhang[17]和Bai[18]等改变邻域搜索策略,有效提高了搜索效率,但路径拐点较多．针对以上问题, 本文拟提出一种改进启发函数的A*算法, 通过改进启发函数的表达式, 引入动态权重因子调整启发函数, 并在累积代价函数前引入权重因子, 以期提高算法搜索效率, 减少算法搜索节点和拐点, 减小路径累积转折角度．

1 改进启发函数的A*算法

1.1 A*算法

A*算法采用总代价评价并选择后续节点的搜索方向, 总代价函数表达式为

f(n)=g(n)+h(n),

(1)

其中g(n)为起始节点n0至节点ni的累积代价; 启发函数h(n)为节点ni至目标节点nt的距离, 提供了对当前状态到目标状态的估计代价或优先级信息, 使算法能够更加有针对性地搜索潜在路径．本文采用欧几里德距离表示启发函数

(2)

其中nix为当前节点横坐标,niy为当前节点纵坐标,ntx为目标节点横坐标,nty为目标节点纵坐标．

1.2 改进A*算法

1.2.1 改进启发函数表达式

为了更好地引导算法搜索方向, 提高算法搜索效率,本文引入子节点(当前节点通过移动、旋转或转换等一步操作即可到达的相邻节点)坐标信息计算启发函数

(3)

其中n(i+1)x为子节点横坐标,n(i+1)y为子节点纵坐标．改进的启发函数可使A*算法借助启发函数信息优先选择潜力更大、更接近目标的路径进行搜索, 并且搜索过程中可略过代价过高或无效的路径, 从而提高搜索效率和缩小搜索空间, 使得算法能够更快地找到最优路径．

1.2.2 动态权重因子调整启发函数

传统A*算法中若当前节点到目标节点之间没有障碍物, 则h(n)与实际路径距离相等, 算法搜索速度快、准确率高, 但实际情况下往往存在障碍物, 路径实际距离大于h(n), 致使算法搜索空间变大, 搜索效率降低．当h(n)→0,f(n)=g(n), 即为Dijkstra算法; 当h(n)≫g(n),f(n)=h(n), 即为广度优先算法(breadth first search, BFS)．若h(n)过小, 则算法扩展节点多, 搜索效率低; 若h(n)过大, 则难以保证所规划路径为最短路径．因此, 适当调整h(n)权重可提高算法性能．当障碍物较少时, 适当增大h(n)权重可缩小算法搜索范围,提高算法搜索效率; 当障碍物较多时, 适当减小h(n)权重可扩大算法搜索范围, 有利于算法寻找最优路径．

本文通过子节点到目标节点障碍物占地面积s1与子节点到目标节点地图总面积s2的比值ρ构造动态权重因子β,调整启发函数, 改进总代价函数

f(n)=g(n)+β·h′(n),

(4)

β=f(ρ)=g(s1,s2,α),

(5)

(6)

(7)

其中α为ρ的调和因子,α∈(0,1); Δnjx和Δnjy分别为横坐标和纵坐标的变化量．通过实验测试不同α值对算法搜索节点N和路径长度L的影响, 设置α的步长为0.01, 结果如表1所示．由表1可知, 当α∈[0.1, 0.57)时, 搜索节点和搜索路径长度均为最小值.本文取α=0.1．

表1 不同α值对应的搜索节点和路径长度

由s1和s2的定义可知,s1≤s2,ρ∈(0,1)．采用对数函数、线性函数、指数函数、sigmoid函数和正切函数构造h′(n)的动态权重因子, 进行仿真测试．图1为函数β=f(ρ)的仿真结果．由图1可知,β与ρ呈正相关,表示障碍物越多,h′(n)权重越大, 不符合算法设计要求．

图1 函数β=f(ρ)仿真结果

为了满足算法要求, 构造函数β=1-f(ρ), 其仿真结果如图2所示．由图2可知: 1) 对数函数的一阶导数β′=-ρ-1, 当ρ→0时,β′→-∞,β→+∞; 当ρ∈(0,1)时,β>1, 表明算法搜索效率有所提高, 但搜索范围小, 易陷入局部最优; 2) 指数函数中β<0, 不能有效引导算法搜索方向; 3) 正切函数中ρ→1时,β<0, 说明障碍物较多时不能正向引导算法搜索; 4) sigmoid函数中β随ρ的变化较小, 说明障碍物对算法搜索的影响不大, 与实际情况不符; 5) 线性函数中ρ→0时,β→1, 相当于传统A*算法;ρ∈(0,1)时,β<1, 相当于减小传统A*算法中启发函数的权重, 虽扩大了搜索范围, 有利于算法逃离局部最优解, 但搜索效率下降．

图2 函数β=1-f(ρ)仿真结果

为达到算法性能要求, 采用对数函数和线性函数构造动态权重因子

β=a0ρ3+a1ρ2+a2ρ+a3,

(8)

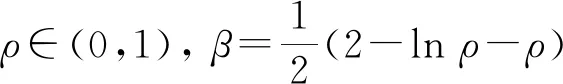
图3为函数β=a0ρ3+a1ρ2+a2ρ+a3的仿真结果．由图3可知: 当ρ∈(0,0.48]时,β>1, 有利于算法缩小搜索空间, 提高搜索效率; 当ρ∈(0.48,1)时,β∈(0,1), 有利于算法扩大搜索空间, 逃离局部最优解; 当ρ=1时,β=0, 表示该区域内全是障碍物, 没有可通行路径．综上, 该函数符合算法设计要求和实际应用场景．

图3 函数β=a0ρ3+a1ρ2+a2ρ+a3仿真结果

1.2.3 权重因子调整累积代价函数

为避免g(n)和h′(n)失去平衡, 本文引入权重因子μ调整累积代价函数, 进一步改进总代价函数

f(n)=μg(n)+βh′(n),

(9)

(10)

其中μ∈(0,1)．求μ的一阶导数

(11)

由此得出,μ′<0,μ为递减函数．当h′(n)为0～100时, 权重因子μ的变化曲线如图4所示．由图4可知: 早期h′(n)较大,μ较小; 随着子节点逐渐靠近目标节点,h′(n)逐渐减小,μ逐渐增大, 有利于提高算法搜索效率．故引入权重因子μ可有效减少算法搜索节点和拐点, 降低路径转折角度, 缩短路径长度．

图4 h(n)′与μ关系曲线

2 实验结果与分析

为验证本文算法的有效性, 选取Dijkstra算法、BFS算法、传统A*算法、调和A*算法和启发函数+B样条改进A*算法等5种路径规划方法与本文改进的A*算法在相同栅格地图中进行路径规划仿真实验, 路径规划结果如图5所示, 图中黑色栅格代表障碍物, 灰色栅格代表算法路径规划过程中的搜索节点, 起始位置标记为△,目标点位置标记为○．每种算法各设置10个实验组, 每组实验对应的平均寻路时间如图6所示．由图6可知, 本文算法的平均寻路时间最少, 且不同实验组之间的平均寻路时间差异较小, 表明该算法的搜索效率最高, 稳定性最好．

图5 不同算法路径规划仿真结果

图6 不同算法的寻路时间对比

为更好地验证本文改进后A*算法的性能, 对比不同算法的路径规划过程中搜索节点、寻路时间、路径长度、路径拐点数和路径转折角度, 结果如表2所示．由表2可知:与Dijkstra算法相比,本文算法搜索节点减少了85.17%, 寻路时间减少了109.648 ms,搜索效率提高了91.88%, 路径长度缩短了6.15%, 路径拐点数减少了28.57%,路径总转折角度减小了40.00%; 与BFS算法相比,本文算法搜索节点减少了18.32%, 寻路时间减少了5.689 ms, 搜索效率提高了37.00%, 路径长度缩短了15.59%, 路径拐点数减少了45.45%, 路径总转折角度减小了50.00%; 与传统A*算法相相比, 本文算法搜索节点减少了51.14%, 寻路时间减少了24.397 ms, 搜索效率提高了75.58%, 路径长度缩短了3.90%, 路径经过拐点数减少了50.00%, 路径总转折角度减小了53.85%; 与调和A*算法相比, 本文算法搜索节点减少了11.57%, 寻路时间减少了7.198 ms, 搜索效率提高了42.63%, 路径长度缩短了30.85%, 路径经过拐点数减少了61.29%, 路径总转折角度减小了73.91%; 与启发函数+B样条改进A*算法相比, 本文算法搜索节点减少了31.41%,寻路时间减少了7.198 ms, 搜索效率提高了42.63%, 路径长度缩短了4.21%, 路径经过拐点数减少了50.00%, 路径总转折角度减小了50.00%．综上得出, 本文改进的A*算法用于路径规划时,搜索节点更少,搜索效率更高, 搜索路径更短, 拐点数更少, 总转折角度更小, 故改进后A*算法具有更好的路径规划性能．

表2 不同算法的路径规划性能指标

3 结论

本文基于子节点到目标节点距离改进A*算法中启发函数的表达式,通过子节点到目标节点障碍物占地面积与子节点到目标节点地图总面积比值构造的动态权重因子调整启发函数, 并以启发函数构造累积代价函数的权重因子．实验结果表明, 改进后A*算法有效减少了搜索节点, 缩短了寻路时间和路径长度, 减少了路径拐点, 降低了路径转折角度, 具有较好的路径规划性能．