带收获率的Lotka-Volterra捕食者食饵趋化扩散模型的Turing不稳定性

张丽丽, 麻作军, 齐 渊

(陇东学院数学与信息工程学院, 甘肃 庆阳 745000)

自20世纪20年代Lotka和Volterra提出经典的捕食者-食饵模型以来, 生物数学家对生物数学进行了广泛深入的研究, 同时结合具体的生态背景和生物意义不断提出更合理的反应函数．在实际生产中, 为了兼顾物种的长期存活以及自然生物链的不间断和最大收获, 学者们建立了带有收获项的捕食者-食饵系统[1-4]．Gupta等[5]对带有Michaelis-Menten型食饵收获项的捕食者-食饵系统进行了稳定性和分支分析, 其他收获率捕食模型的研究参见文献[6-10]．本文拟考虑带收获率的Lotka-Volterra捕食者-食饵模型

(1)

其中u(t)和v(t)分别表示食饵和捕食者在t时刻的种群密度; 生命系数Γ,r,γ,h都是正参数, 分别表示捕食者的增长率、食饵的增长率、食饵的死亡率和收获率．根据Keller等[11]针对细胞向信号物质浓度高的区域聚集现象提出的趋化模型, 可得模型(1)的趋化模型为

(2)

1 模型的稳定性与趋化导致的不稳定性

(3)

对系统(3)在(0,0)处进行线性化处理,得近似方程

(4)

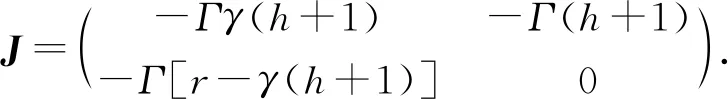
(5)

则系统(4)可转化为

(6)

λ2-T2(k)λ+H2(k2)=0,

(7)

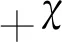
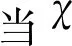
是H2(k2)=0的2个根．

注2由于trL2k≠0, 故该趋化系统不会出现Hopf分支．

2 数值模拟与讨论

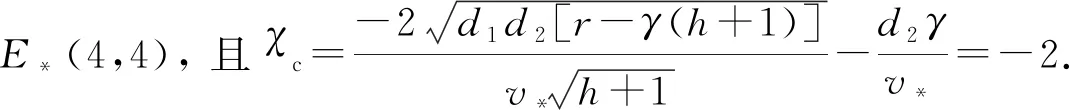
图1 食饵种群密度随时间和空间的变化趋势

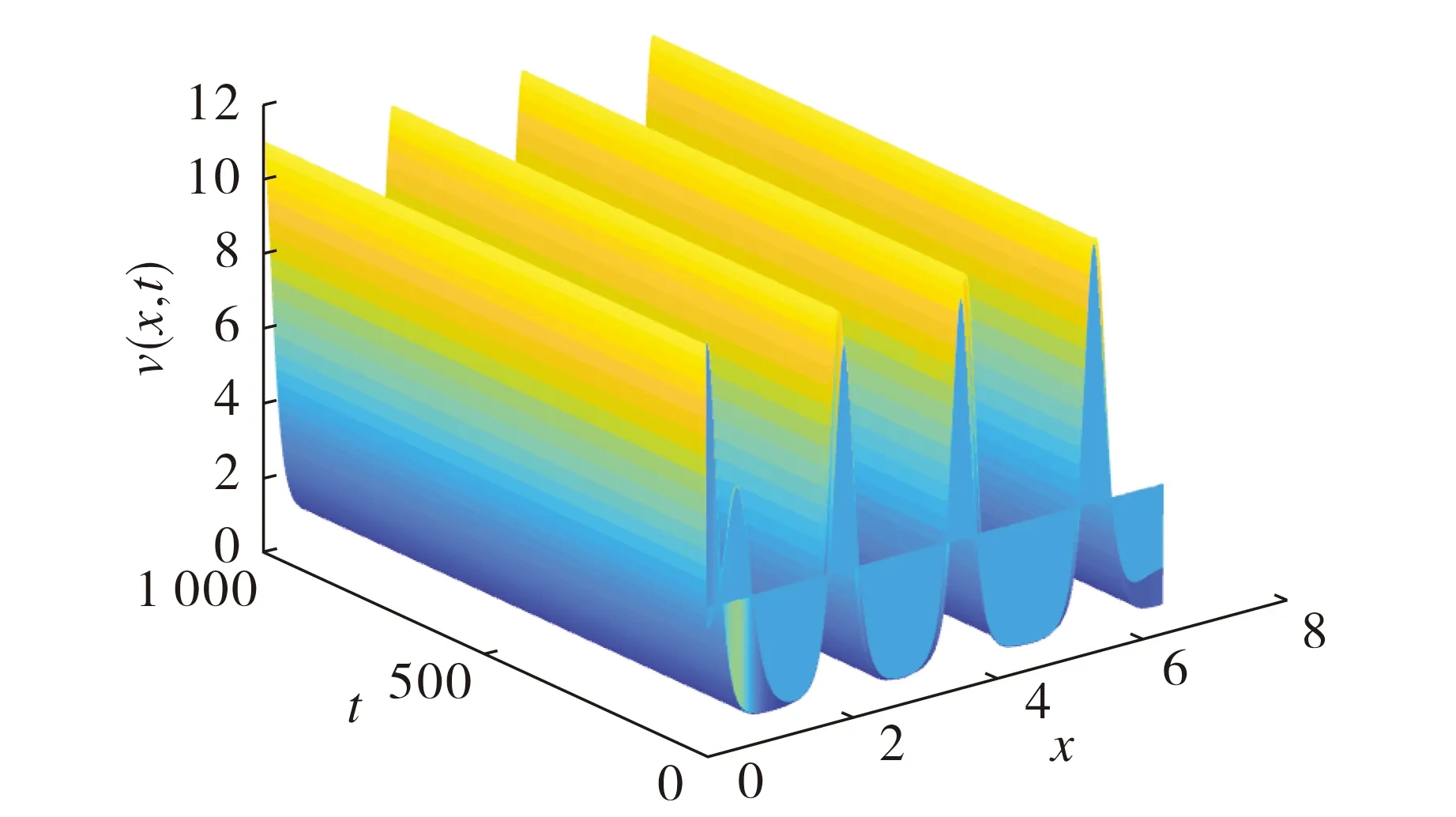
图2 捕食者种群密度随时间和空间的变化趋势