n-SG(,,)模

孔留贞

(南京工程学院数理学院, 南京 211167)

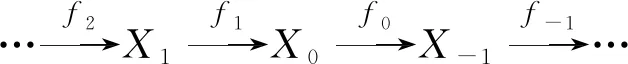
1 预备知识

文中所有的环R都有单位元, 所有的模都是左模,R-Mod为左R-模范畴．不特别声明时,X,Y,Z为R-Mod的加法满子范畴, 且X⊆Y,X⊆Z．

2) 设X·是模M的1个X-分解(或X-余分解), 若对任意的Y∈X, 序列HomR(Y,X·)(或HomR(X·,Y))是正合的, 则称X·是proper(或coproper)的[23-25]．

3) 如果R-Mod的1个子范畴X满足: 对任意的正合列0→X′→X→X″→0,X′∈X,X″∈X当且仅当X∈X, 则称X是epic-admissible正合[26]．如果X是epic-admissible正合且所有投射模均属于X, 则称X投射可解[27]．

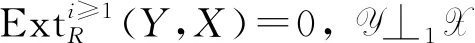
6)n和m的最大公因子记为(n,m)．

2 n-SG(,,)-模

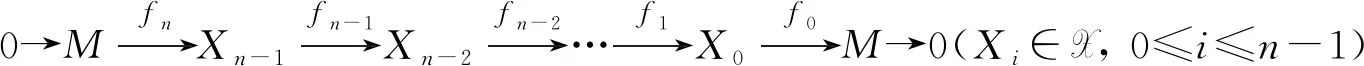
若X=Y=Z是投射/内射/平坦模范畴, 则n-SG(X,Y,Z)-模是n-强Gorenstein投射/内射/平坦模[20]．正合列具有如下性质:

定理2设Y⊥X,X⊥Z且⊥1X=X．对任意M∈R-Mod,n≥1, 下列结论等价:

1)M∈n-SG(X,Y,Z);

2) 存在1个正合列

(1)

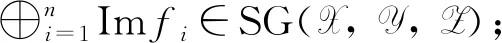
证明 1) ⟹2)．设M是1个n-SG(X,Y,Z)-模, 若存在1个正合列(1)满足HomR(Y,-)-正合和HomR(-,Z)-正合, 则可得正合列

类似地, 对所有的0≤i≤n-1,有正合列

其中λ′为嵌入, 故可得正合列

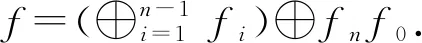
2)⟹3)⟹5)及2)⟹4)⟹5)是平凡的．

5)⟹1)．对任意的0≤i≤n-1,有正合列

0→Imfi+1→Xi→Imfi→0．

(2)

下面讨论m-SG(X,Y,Z)-模与n-SG(X,Y,Z)-模之间的关系．文献[21]例3.2说明当n不能整除m时,n-SG(X,Y,Z)-模不是m-SG(X,Y,Z)-模．但当n|m时, 则有下列结论．

引理3若n|m, 则n-SG(X,Y,Z)⊆m-SG(X,Y,Z)．

证明 设m=kn,k∈Z+,M∈n-SG(X,Y,Z)．存在1个正合列(1)满足HomR(Y,-)-正合和HomR(-,Z)-正合．2个这样的正合列相连接得到正合列

因该正合列满足HomR(Y,-)-正合和HomR(-,Z)-正合, 故M∈m-SG(X,Y,Z)．证毕．

为了给出m-SG(X,Y,Z)-模与n-SG(X,Y,Z)-模之间的关系, 有以下2个命题．

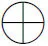
(3)

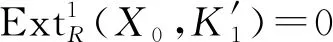
图1 X′0 →M与X0→M的拉回图

命题51) 若n|m, 则n-SG(X,Y,Z)∩m-SG(X,Y,Z)=n-SG(X,Y,Z);

2) 设Y⊥X且X在满同态的核下封闭．若n|/m,m=kn+j, 其中k∈Z+, 0

证明 1) 由引理3易得．

图2 Xkn→Kkn与MX→Kkn的拉回图

图3 D→MX与M→MX的拉回图

定理6n-SG(X,Y,Z)∩m-SG(X,Y,Z)=(n,m)-SG(X,Y,Z)．

证明 由命题5和辗转相除易证．

推论7n-SG(X,Y,Z)∩(n+1)-SG(X,Y,Z)=SG(X,Y,Z)．特别地, ∩n≥2n-SG(X,Y,Z)=SG(X,Y,Z)．

推论8[21]n-SG-Proj(R)∩m-SG-Proj(R)=(n,m)-SG-Proj(R), 其中Proj(R)记作投射R-模范畴．