四元数偏移分数阶傅里叶变换的性质及其应用

杨河河, 冯 强

(延安大学数学与计算机科学学院, 陕西 延安 716000)

分数阶傅里叶变换(fractional Fourier transform, FRFT)[1]是一种重要的时频分析工具. 由于FRFT有1个自由参数, 所以它比无参数的傅里叶变换(Fourier transform, FT)更加灵活, 并被广泛用于求解微分方程[2]、信号分析与处理[3-4]和图像处理[5-6]等．Hamilton[7]于1843年提出的四元数在数学、计算机与工程学等领域有重要的应用．近年来, 众多学者将经典的积分变换拓展到四元数域, 并取得了一系列研究成果．Cheng等[8]研究了四元数傅里叶变换(quaternion Fourier transform, QFT)的Plancherel定理、反演定理以及四元数傅里叶变换的一些重要性质; El Haoui等[9]研究了双边四元数傅里叶变换的Benedicks等不确定性原理; Tefjeni等[10]定义了右边四元数小波变换(quaternion wavelet transform, QWT), 研究了四元数小波变换的重要性质及相关的不确定性原理; Xu等[11]定义了四元数分数阶傅里叶变换(quaternion fractional Fourier transform, QFRFT), 并研究了QFRFT的可逆性、线性性质、奇偶不变性及可加性等性质, 推导出四元数分数卷积定理、四元数分数相关定理以及四元数分数乘积定理; 付志远等[12]在四元数域上定义了分数阶傅里叶变换, 研究了该变换的平移、调制和Plancherel定理等性质及其在微分方程中的应用; Li等[13]研究了双边QFRFT与帕塞瓦尔恒等式的一些微分性质; Mei等[14]定义了双边加窗四元数分数阶傅里叶变换(quaternion windowed fractional Fourier transform, QWFRFT), 研究了QWFRFT的卷积定理以及加窗四元数分数卷积算法及其复杂度分析．

偏移分数阶傅里叶变换(offset fractional Fourier transform, OFRFT)[15]是分数阶傅里叶变换的进一步拓展, 由于OFRFT较FRFT多2个自由参数, 所以在非平稳信号处理中比FRFT更灵活．近年来, 虽然对四元数分数阶傅里叶变换的理论及其应用的研究日趋活跃, 但是对四元数偏移分数阶傅里叶变换的研究仍处于零散状态. 由于四元数偏移分数阶傅里叶的微分性质在求解微分方程中起着至关重要的作用, 所以从数学与工程的角度出发, 有必要进一步研究四元数偏移分数阶傅里叶变换的相关性质及应用．本文拟将偏移分数阶傅里叶变换拓展到四元数域, 通过定义左边四元数偏移分数阶傅里叶变换, 讨论其基本性质, 并将其应用于研究一类线性偏微分方程的解．

1 预备知识

1.1 四元代数

设ei(i=1,2)是向量空间R2的标准正交基, 则四元数代数空间H的基是1,e1,e2,e12, 故H中任意元素q都可以表示为q=q0+e1q1+e2q2+e12q3, 其中q0,q1,q2,q3∈R, 且e1,e2,e12遵循如下法则:

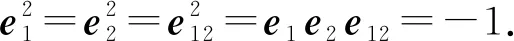
将q的标量部分记为q0=Sc(q), 矢量部分记为Vec(q)=e1q1+e2q2+e12q3, 则四元数p,q的乘法为

qp=q0p0-Vec(q)·Vec(p)+q0Vec(p)+p0Vec(q)+Vec(q)×Vec(p)．

下面给出与四元数有关的一些重要定义和引理．

定义1设L1(R2;H),L2(R2;H),S(R2;H)为3个四元数值的函数空间,其中

S(R2;H)={f|f∈C∞(R2;H), supx∈R2(1+|x|k)|∂αf(x)|<+∞},

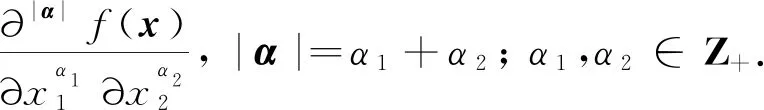
定义2设函数f,g:R2→H, 则f与g的内积与标量积分别定义为

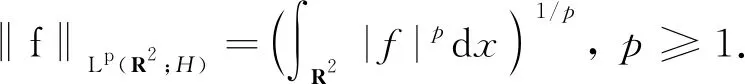
引理4[16]设f1,f2∈L2(R2;H),则有

1.2 四元数分数阶傅里叶变换

定义5设f∈L2(R2;H), 则f(x)的左边四元数分数傅里叶变换定义为

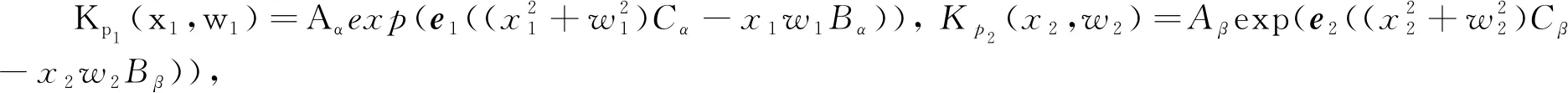
2 主要结果

定义6设四元函数f∈L1(R2;H), 且ei是一维向量,i=1,2,θi≠niπ, 则左边四元数偏移分数阶傅里叶变换定义为

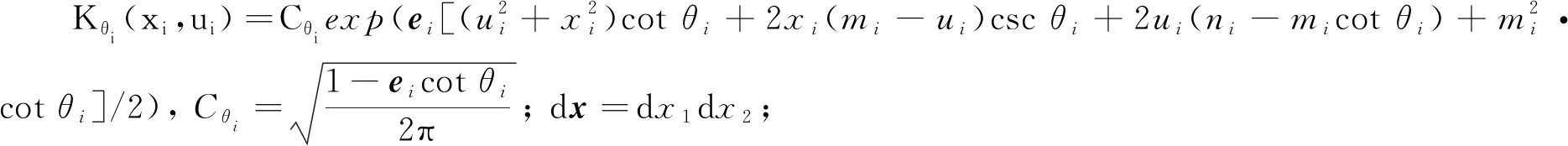
定义7设f∈L1(R2;H), 则左边四元数偏移分数阶傅里叶变换的逆变换定义为

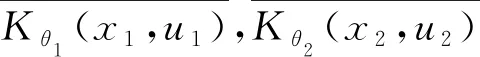
下面给出QOFRFT与QFT的相互关系．

下面探究左边四元数偏移分数阶傅里叶变换的基本性质．

定理9设f1,f2∈L1(R2;H), 常数a,b∈R, 则

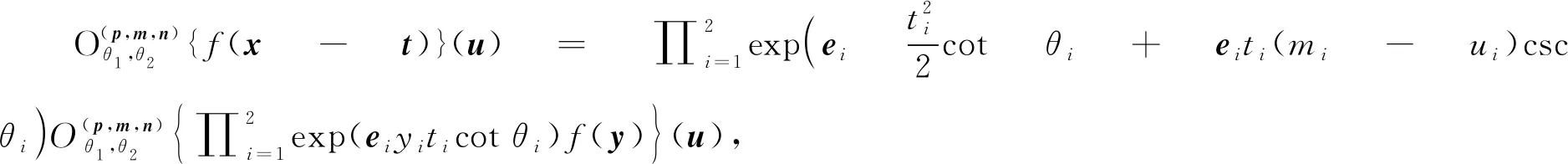
下面讨论左边四元数偏移分数阶傅里叶变换的微分性质．

定理11设f∈S(R2;H),有

其中i=1,2．

定理12设f∈S(R2;H),有

其中i=1,2．

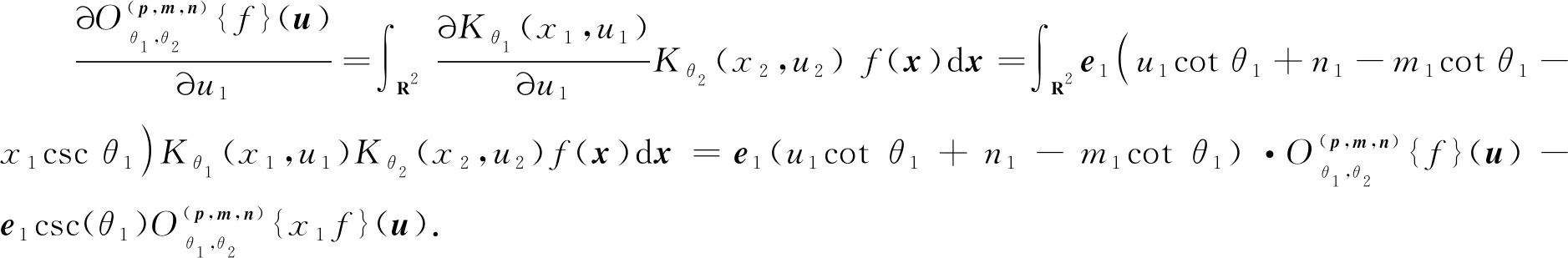
同理, 当i=2时, 结论类似可证．

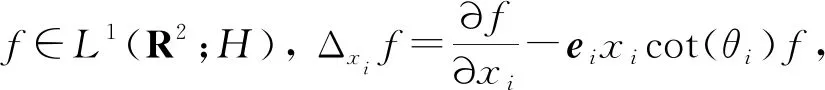
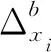
其中i=1,2．

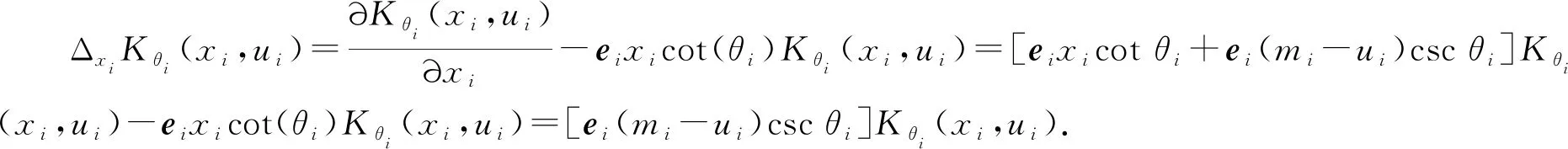
由定理13可得以下推论．

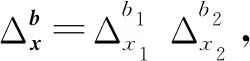
其中i=1,2.

定理15设f∈L1(R2;H), 则对于任意b∈Z+, 有

其中i=1,2．

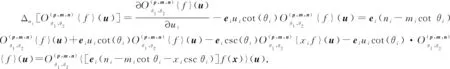
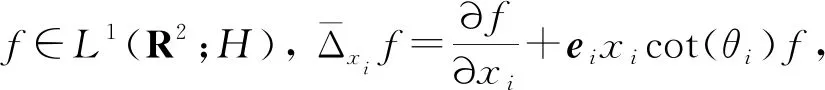
其中i=1,2．

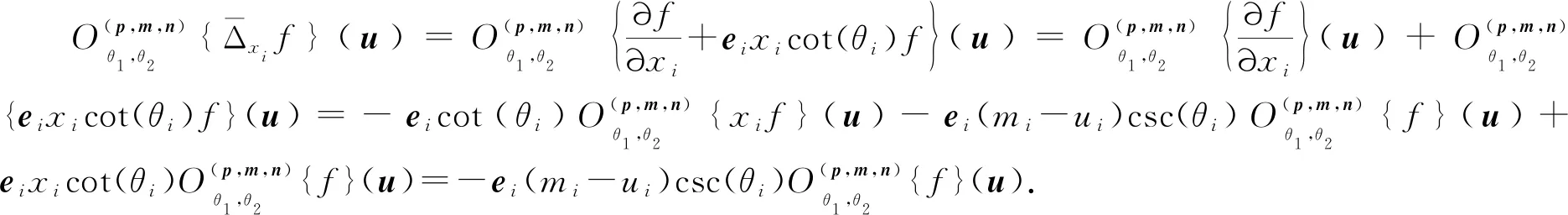
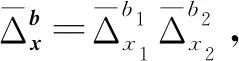
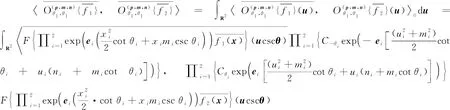
特别的, 当f1=f2时, 可得以下推论．

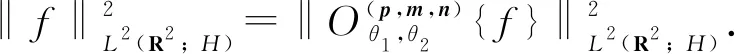
证明 由范数的定义, 得

下面利用QOFRFT的微分性质给出一类线性偏微分方程的显式解．

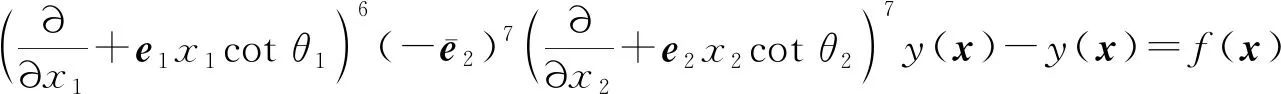
在此式两端取左边四元数偏移分数阶傅里叶变换的逆变换, 得