直升机电传飞控作动布局研究

李修赫,刘海清,焉台郎,万兴云,聂文明

(中国直升机设计研究所,江西 景德镇 333001)

0 引言

电传飞控系统是直升机电气综合控制的纽带和主动控制技术的基础[1-3]。电传飞控系统的使用极大地提高了直升机的操纵品质、任务效能和战场生存性[1,4-5]。国外新一代高性能直升机均采用了先进的多余度全权限数字式电传飞行控制系统[6-10]。国内未来直升机型号设计将广泛采用电传飞控系统;现有型号的机械操纵系统也将逐步进行电传飞控系统的改装升级[11-12]。

电传飞控系统设计的一大难点在于,如何在已经确定操纵量范围和桨距角范围的情况下,完成作动布局,即确定作动器位置并计算相应行程。因操纵量与桨距角呈线性关联,故只需研究桨距角与作动布局的对应关系。在机械操纵系统中,桨距角与作动布局的对应关系由机械传动链确定。国内目前采用机械操纵系统的直升机型号,其作动器位置相对固定,且尚未对作动器位置和行程进行准确解耦。然而,未来直升机型号将以结构形式新、起飞重量大作为主要特点[13-15],给直升机作动布局设计带来一系列问题:主减壳体形状独特、作动器尺寸偏大、液压管路复杂[16-19]等等。上述因素必然导致作动器的位置选择更加灵活自由,需要对作动器的位置和行程准确解耦,使得在作动器的位置自由改变时,能够计算出相应的作动器行程,满足未来直升机型号设计需求。

因此,本文对直升机电传飞控作动布局进行研究。通过简化结构交联与几何关系推导,得到桨距角与作动布局的对应关系;以此为基础建立仿真模型进行数字仿真,并将仿真值与实测值进行对比,为未来直升机电传飞控系统的研发设计提供了理论支撑。

1 直升机电传飞控作动原理

图1为直升机电传飞控作动原理示意图。其中,作动器下端固定在主减壳体上,上端连接自动倾斜器不动环;不动环与动环之间轴承连接,变距拉杆连接动环与桨叶根部的变距摇臂。当存在输入信号时,三台作动器协调伸缩,带动不动环和动环倾转,通过变距拉杆和变距摇臂传递运动,实现桨叶变距。

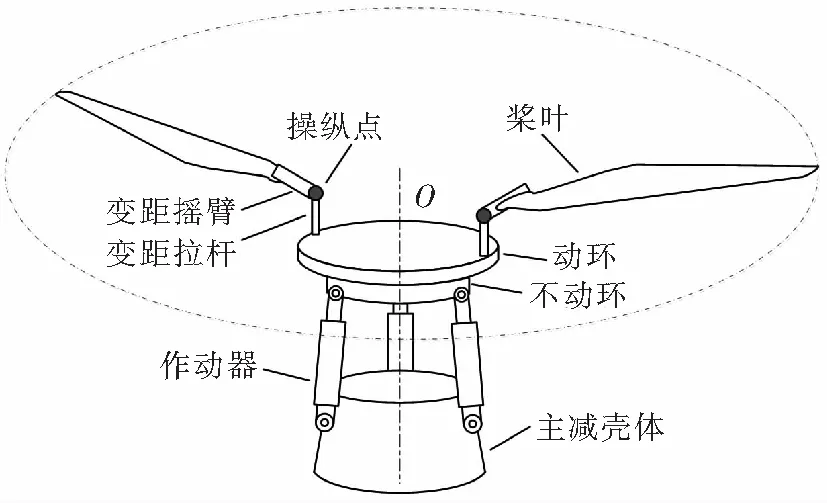
图1 直升机电传飞控作动原理示意图

2 直升机电传飞控作动布局解算

为简化结构交联,在动环、不动环和桨盘平面建立虚拟变距轴,如图2所示。定义动环、不动环和桨盘平面的横向虚拟变距轴在同一垂面内,且方向一致,三者可以投影为一条直线;定义动环、不动环和桨盘平面的纵向虚拟变距轴在同一垂面内,且方向一致,三者可以投影为一条直线。定义主桨叶旋转方向为逆时针方向,纵向虚拟变距轴与前作动器的夹角为提前操纵角φ;提前操纵角φ的位置沿旋转方向提前于前作动器,其大小由旋翼结构确定。左作动器与前作动器的夹角为α;右作动器与前作动器的夹角为β。

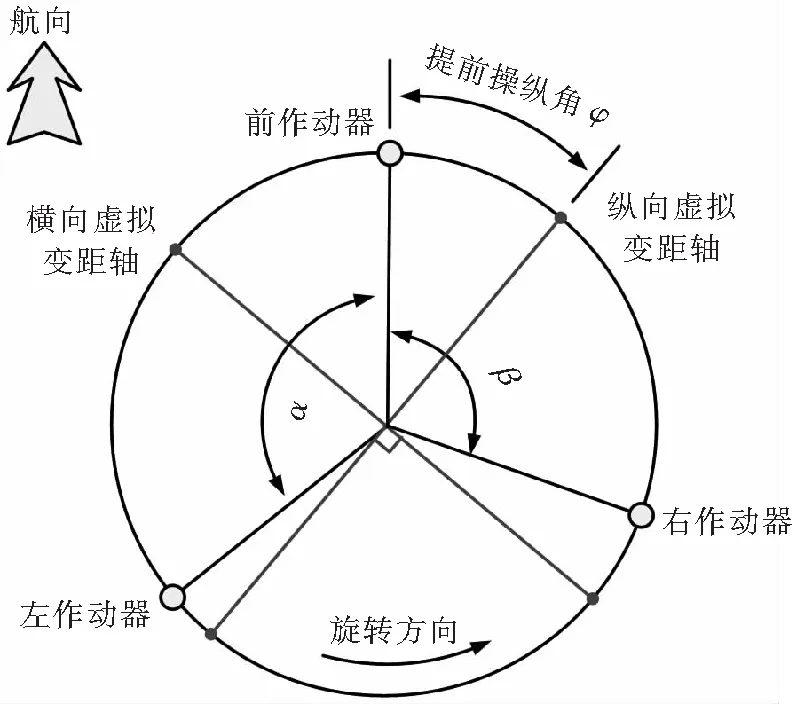
图2 虚拟变距轴

当存在桨距角θ时,根据角度与弧度的关系可以得出操纵点行程S0:

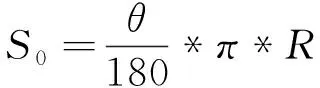
(1)

其中,R为变距摇臂长度,则动环在虚拟变距轴的行程为:

S0=S动

(2)

根据动环和不动环的传动比,计算不动环在虚拟变距轴的行程为:

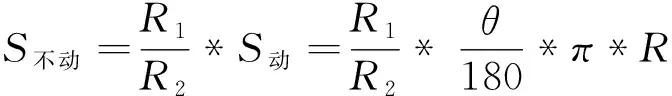
(3)

其中,R1为不动环半径,R2为动环半径。

根据不动环在虚拟变距轴的行程S不动折算三台作动器的行程,前作动器运动几何关系如图3所示,左、右作动器运动几何关系与其相同。

存在纵向操纵对应桨距角θ纵输入时,横向变距轴保持不动,纵向变距轴绕横向变距轴转动θ纵,可求出此时三台作动器的行程分别为:

(4)

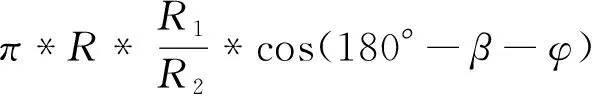
(5)

( 6)

存在横向操纵对应的桨距角θ横输入时,纵向变距轴保持不动,横向变距轴绕纵向变距轴转动θ横,可求出此时三台作动器的行程分别为:

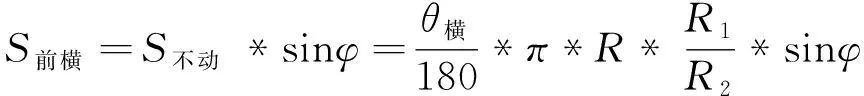
(7)

(8)

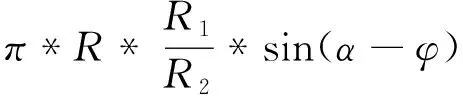
( 9)

存在纵向+横向组合操纵对应桨距角输入时,横向变距轴绕纵向变距轴转动θ横,纵向变距轴绕横向变距轴转动θ纵,可求出此时三台作动器的行程分别为:

S前=S前纵+S前横

(10)

S左=S左纵+S左横

(11)

S右=S右纵+S右横

(12)

当主桨叶旋转方向为顺时针方向时,S前保持不变,S左与S右的解算公式互换。至此,完成直升机电传飞控作动布局解算,即选定作动器位置后,可根据桨距角输入,求解每台作动器的行程。

3 直升机电传飞控作动布局仿真模型

为了验证本文解算方法的准确性,选取一直升机作为验证对象。该机主桨叶旋转方向为逆时针方向,前作动器安装在主减速器正前方,左、右作动器与之呈120°夹角。

通过Matlab/Simulink仿真软件建立直升机电传飞控作动布局仿真模型,将该机参数作为模型输入值,模型主体部分包括桨距角输入、不动环半径/动环半径、弧度转换、变距摇臂长度、提前操纵角、各作动器位置关系、桨距角行程极限和作动器行程极限等,如图4所示。

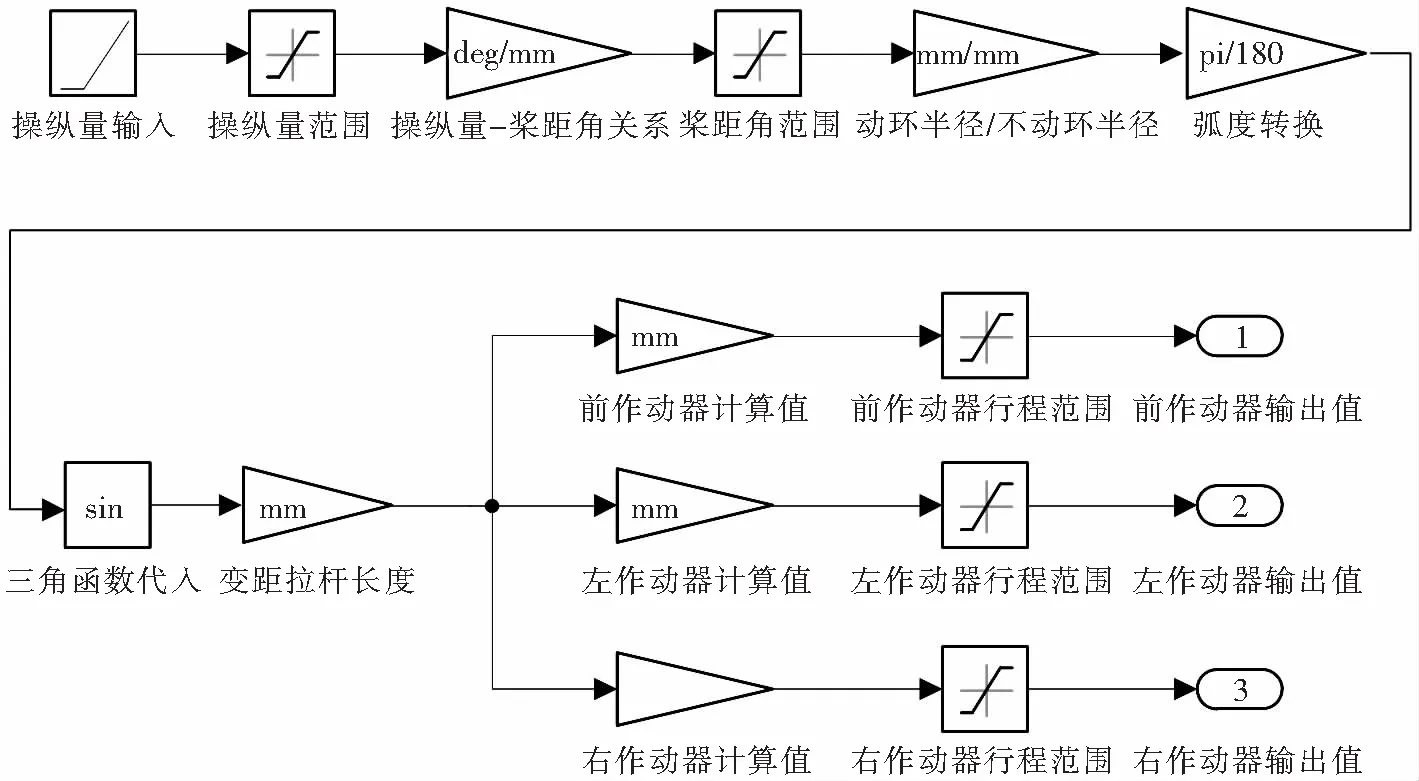
图4 直升机电传飞控作动布局仿真模型

4 结果分析

在外场对该机进行了多组桨距角与作动器行程测量,在测量数据的基础上,对桨距角全范围进行拟合,并得到了对应的作动器行程。图5为实测值与仿真值对比图。结果表明,在桨距角全范围内,作动器行程的仿真值与实测值基本吻合。仿真值覆盖区域相比于实测值覆盖区域整体略微偏上,即仿真值的作动器伸出量略大于实测值的作动器伸出量,仿真值的作动器缩回量略小于实测值的作动器缩回量。

图5 作动器行程对比

图6为直升机桨叶变距示意图。在实际变距时,作动器与旋翼结构的协调运动,保证了桨盘平面能够按照设计要求倾斜相应角度,完成桨叶变距[20]。本文在虚拟变距轴内对桨盘平面倾斜向作动器行程推导的过程中,简化了作动器绕支座的小角度转动和旋翼结构沿直升机Z轴的平移及绕直升机Z轴的转动,这是作动器行程误差产生的主要原因。

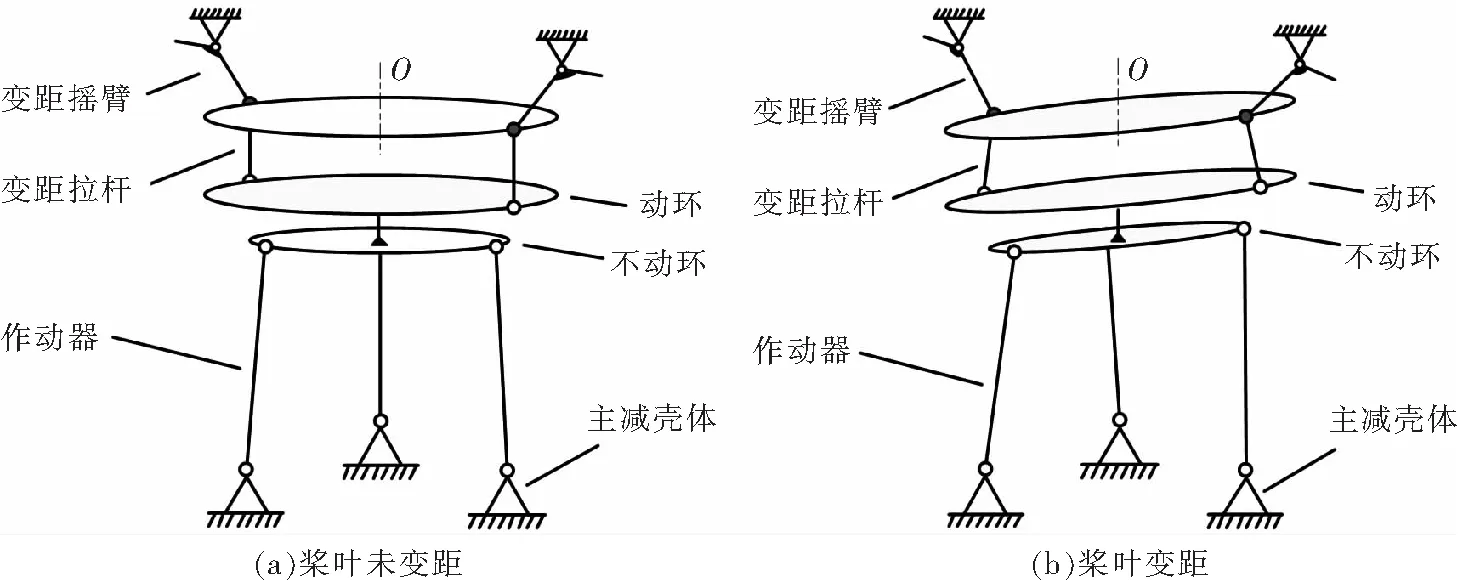
图6 直升机桨叶变距示意图

为了评估简化造成的误差,选取极限组合操纵对应的桨距角作为输入,对实测值和仿真值进行详细分析。极限组合操纵作为衡量直升机作动设计的重要手段,广泛应用于型号设计验证[21]。本文选取的极限组合操纵包括:前极限+左极限、前极限+右极限、后极限+左极限、后极限+右极限。图7为极限组合操纵时的作动器行程。

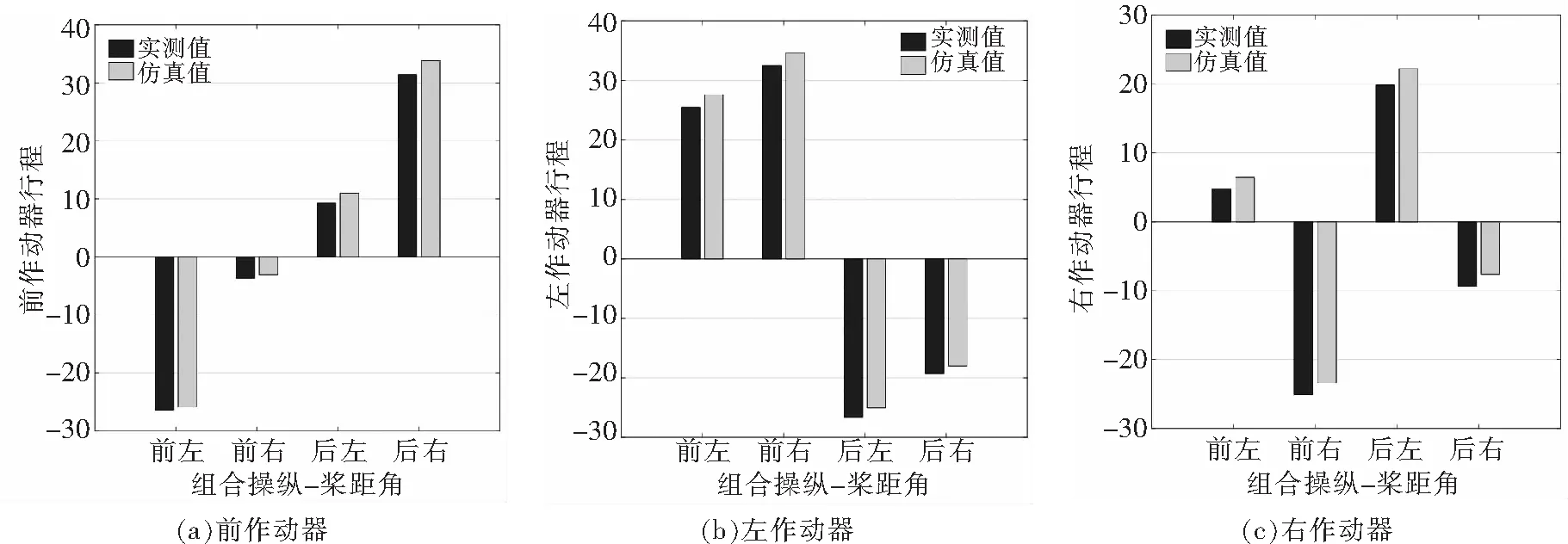
图7 极限组合操纵时的作动器行程。

结果表明,前作动器行程最大误差出现在后极限+右极限工况,实测值31.45 mm,仿真值33.84 mm,行程误差2.39 mm;左作动器行程最大误差出现在前极限+左极限工况,实测值25.49 mm,仿真值27.60 mm,行程误差2.11 mm;右作动器的最大误差出现在后极限+左极限工况,实测值19.87 mm,仿真值22.25 mm,行程误差2.38 mm。综上所述,各作动器行程实测值与仿真值误差均不超过3 mm,满足直升机作动设计精度要求。表1给出了各作动器行程统计。

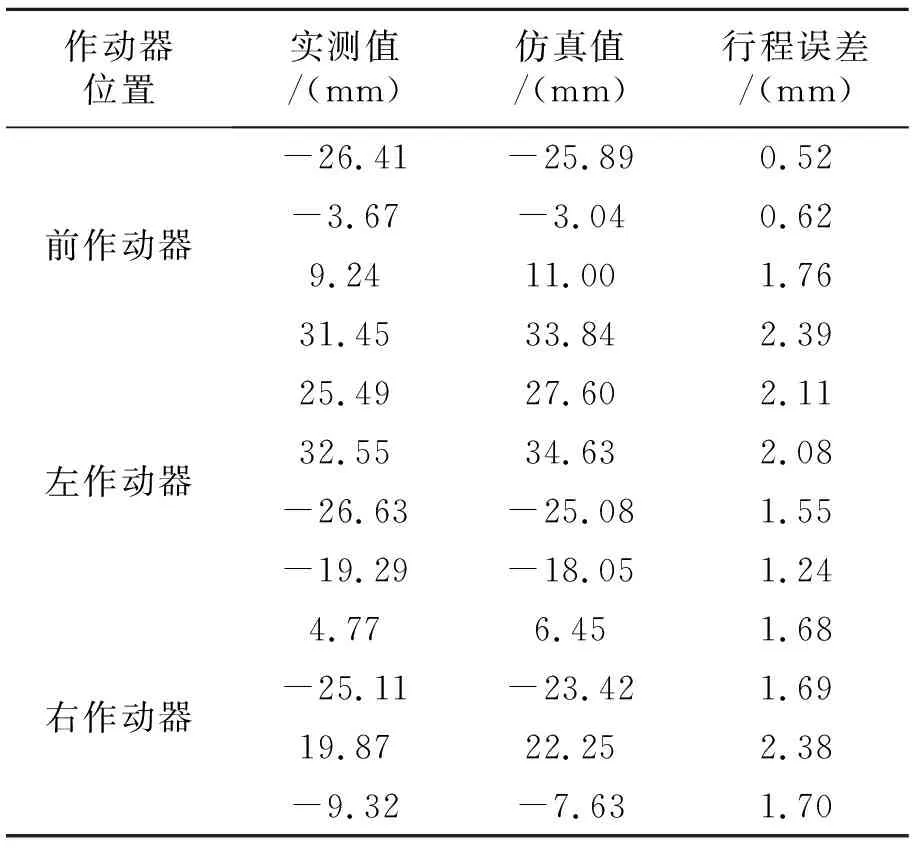
表1 各作动器行程统计

5 结论

本文以直升机电传飞控作动布局为研究对象,通过简化结构交联与几何关系推导,得到了桨距角与作动布局的对应关系,建立了数值仿真模型,并将仿真值与实测值进行了对比,得出了以下结论:

1) 仿真值与实测值误差不超过3 mm,符合直升机作动设计标准,能够满足未来直升机型号设计需求。

2) 对作动器位置和行程进行了准确解耦,可根据设计需要自由选定作动器位置并计算相应行程。

3) 现有直升机型号的机械操纵系统在改装电传飞控系统时,亦可参考本文研究进行作动布局设计。