直升机漂浮能力估算方法及数值验证

朱俐宇,臧 波

(1.中国直升机设计研究所,江西 景德镇 333001;2.海军装备部驻武汉地区军事代表局,湖北 武汉 430060)

0 引言

在目前统计的直升机水上迫降事故中,多数直升机都会在迫降到水面的数分钟内迅速沉没,仅有少数直升机在迫降后可以稳定正浮于水面之上;而这之中又有部分直升机在后续漂浮过程倾翻[1]。直升机在实际水面迫降时,所处的水域环境往往是较为恶劣的海洋环境,风、浪、洋流等复杂条件不仅会使得直升机在漂浮时的姿态更难以维持稳定,也会为乘员安全撤离增加一定的难度与风险。如何增强直升机漂浮稳定性,延长直升机的漂浮时间,以保障机内人员安全撤离舱室等待救援,是目前海上直升机的重点研究方向之一。

目前国内外对于直升机漂浮能力研究的方法分为三种。第一种为全尺寸模型试验,即采用真实的直升机或等比例的模型进行漂浮试验验证。该方法所得试验数据可信度高,试验结果说服性强。但由于试验成本较大,试验准备工作与收尾工作较为复杂,试验周期较长,多数直升机公司更愿意采用第二种研究方法,即以弗劳德数为主要相似准则数的缩比模型试验方法。该方法试验流程简单,可重复性强,试验结果较为可信。但由于该方法一般需要在波浪水池中进行试验,因而试验工况受限于水池的长度、宽度、造波能力等现实条件,无法完全体现出直升机在真实海洋环境中的漂浮特性;并且该方法对缩比模型的加工精度要求较高,使得模型制造同样存在一定难度。而第三种方法,即数值模拟法,则具有较为明显的优势:试验周期短,试验成本低,且可以根据需要模拟不同的复杂的海况,其模型精度仅受限于理论的发展。目前公开的直升机漂浮稳性研究文献中,多是采用该种方法。

本文首先给出直升机稳性计算方法,并基于以往直升机漂浮能力设计经验,给出直升机漂浮能力范围估算方法。采取基于势流理论的数值计算方法,对直升机漂浮能力范围及边界进行了计算,验证了上述方法的准确性。

1 计算方法

1.1 势流理论

为简化直升机漂浮问题的求解,节约计算时间,本文采用基于势流理论的计算方法。该理论假设流体无粘、不可压缩,对于含有运动刚体的波浪流场,其速度势可表示为:

φ(x,y,z;t)=φr+φω+φt

(1)

式中,φr为辐射势,与刚体的运动有关;φω为简谐波浪初始入射势;φt为波浪穿过刚体后的绕射势。

上述势函数需满足拉普拉斯方程:

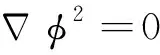
(2)

同时需满足海底表面条件:

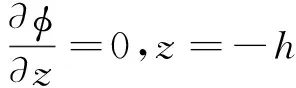
(3)

自由表面条件:

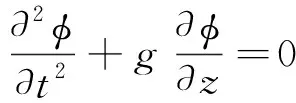
(4)

刚体表面不可穿透条件:

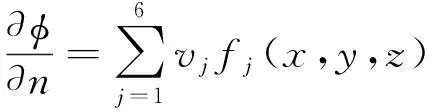
(5)

通过以上方法计算出流场的速度势函数后,可通过线性伯努利方程求得流场压力:

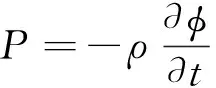
(6)

则运动刚体所受流体力可通过压力对湿表面的积分获得。

1.2 大倾角稳性计算

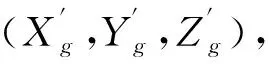
(7)

式中,n1、n2、n3为机体面元单位法向量的三个分量,ps为静水压力。

1.3 风倾力矩及直升机抗侧风能力估算

对于受海风扰动的直升机,其所受风倾力矩计算式如下:

Mw=1/2ρACDSel(Vw)2

(8)

式中,ρA为空气密度;CD为直升机气动阻力系数,在本文中以CFD方法算得;Se为直升机水上部分迎风投影面积;l为力臂,即气动中心与水线间的距离;Vw为风速。

当直升机最大恢复力矩MRmax已知时,令Mw=MRmax,即可求得直升机在静水中可承受的最大风速Vwmax:

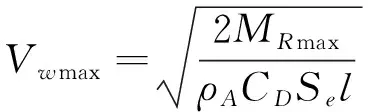
(9)

1.4 直升机漂浮能力估算方法

直升机的漂浮能力,指直升机在特定海域环境下满足稳定漂浮,不倾覆、不沉没的能力。评定直升机漂浮能力的重要指标为直升机在一定时间内漂浮运动的横摇幅值。对于一外形及重量、重心均已确定的直升机,其漂浮能力仅受海洋环境的影响。下面给出直升机漂浮能力的估算方法。

通过对直升机的静稳性计算可获取直升机横摇方向幅值响应算子(Response Amplitude Operators, RAO)曲线。RAO含义为直升机在固定频率的规则波中,横摇方向上运动幅值与波幅的比。即可理解为,对应频率下浪高每增加1 m,直升机横摇运动幅值增加的角度值。曲线的最大值所对应的频率则为直升机横摇运动的固有频率,直升机在该频率的规则波中的横摇运动最为剧烈。直升机稳性消失角与该曲线最大值的比值,则为无风时直升机最大可承受的浪高。

已知直升机抗侧风与承受波高的能力的边界,则可选定一定风速,将波高由直升机最大可承受波高开始按一定间隔下降,并进行模拟计算,直至直升机不再倾覆。此时获取的波高即为对应风速下的直升机最大可承受的波高。将直升机可承受的风速-波高绘制成一条曲线,曲线与横轴和纵轴所包围的面积即代表直升机的漂浮能力。取每个海况所对应的最大波高与风速并拟合成曲线,得到标准海况曲线。该曲线与直升机耐波性边界曲线的交点即为直升机在标准海况下的最大漂浮能力,如下文中图3所示。

1.5 波浪与风模拟理论

对于规则波浪,选取Ariy线性波理论进行模拟,其波面方程为:

η=αcos(kx-ωt)

(10)

式中,a为波幅值,k为波数,ω为波浪圆频率。直升机在海上漂浮时所处水域环境大部分为深水条件,则波浪周期:

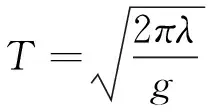
(11)

式中,λ代表波长。

对于不规则波浪,本文采用P-M谱进行模拟,其波谱表达式为:

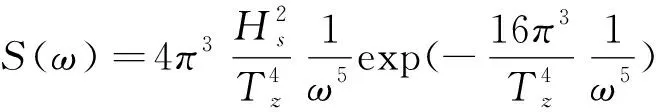
(12)

式中,Hs为有义波高,Tz为过零周期,其与波峰周期T0和平均波周期T1关系为:

T0=1.408Tz

T1=1.086Tz

(13)

对于风场则是采用海洋工程界广泛使用的NPD谱进行模拟。其对海平面上方高度为zm处的一小时内的平均风速定义为:

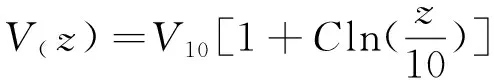
(14)

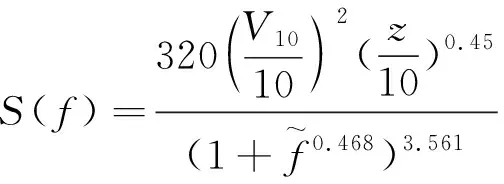
(15)

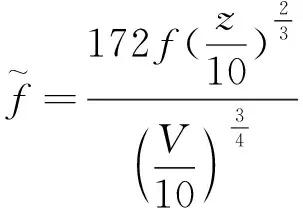
(16)

2 计算结果及分析

2.1 直升机静稳性及耐波性分析

图1给出了直升机绕水平轴的恢复力矩曲线,该曲线表征直升机抗侧倾的能力。从图中可以看到,直升机在倾角为22°时获得最大恢复力矩,其值为20.6 kN·m。而当倾角达到52°时,直升机稳性消失,不再具有自主恢复至平衡位置的能力。根据式(9)可计算出,当没有波浪时,加装了漂浮装置的直升机可抗54 m/s的侧风。

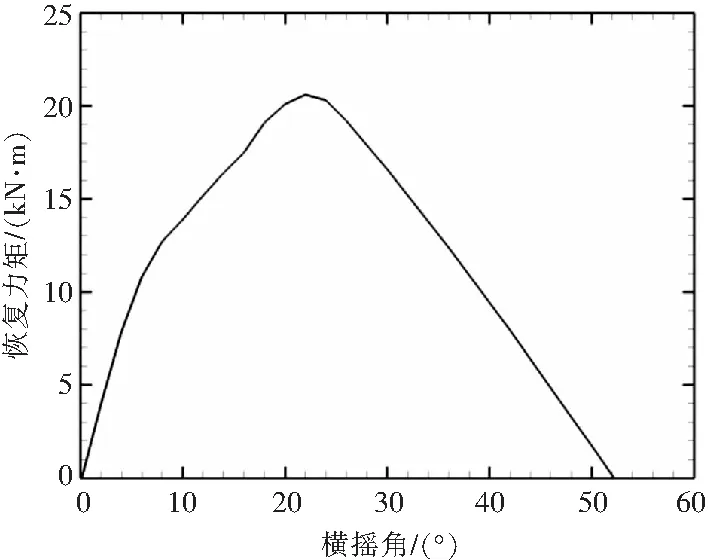
图1 横摇角度-恢复力矩曲线图

图2给出了加装了漂浮装置的直升机RAO与本文所采用的波浪环境的90°浪向波浪谱曲线。从图中可以看到,直升机横摇固有频率ω=0.32 Hz,对应的RAO为8.87 °,则当无风时直升机最大可承受波高为5.86 m。在0.73 Hz时,RAO出现二次峰值,直升机在该频率下的谐振运动是由机体两侧漂浮装置所主导的。从波浪谱曲线可以看出,波浪部分能量在直升机横摇响应范围内,但谱峰频率与直升机固有频率还有一定距离,故可预测直升机在给定环境条件90°浪向下的横摇运动较为温和。

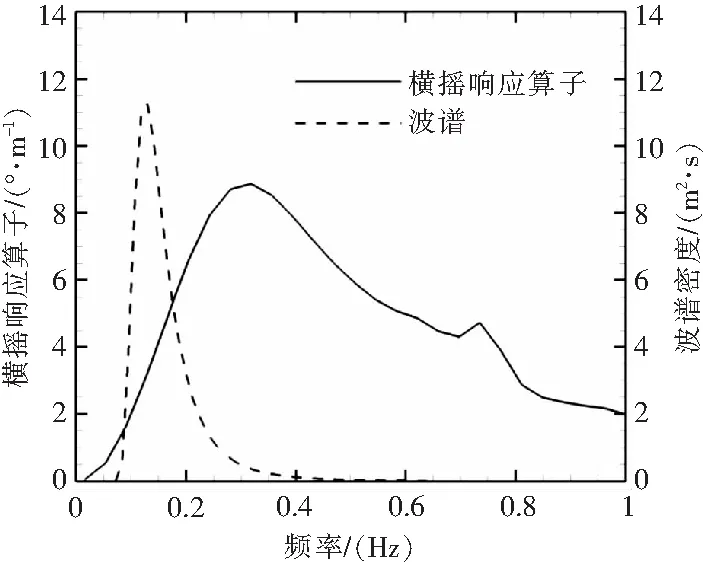
图2 波谱与直升机横摇方向RAO

图3通过1.3节、1.4节中的分析方法,给出了加装了漂浮装置的直升机的耐波能力。从图中可得,该直升机在标准海况下可承受14.8 m/s的风速,对应波高为4.5 m。根据海浪等级划分标准,五级海况对应的最大有效波波高为4 m,可见该机具有在五级海况中稳定漂浮的能力,满足AC-29规章规定的直升机应在四级及以上海况保持稳定的要求。

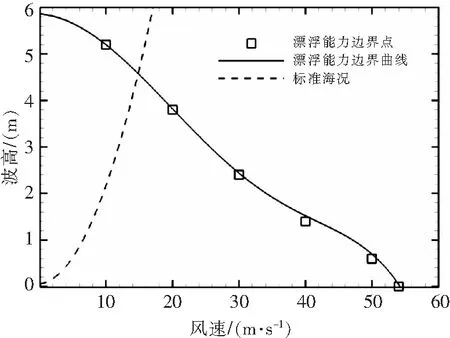
图3 直升机漂浮能力

2.2 直升机五级海况漂浮能力验证

上文模拟直升机最大可承受波高时,采用的水域环境为规则波,而实际上直升机进行迫降漂浮时,所面临的水域环境往往是更为复杂的不规则波浪。因此,需要对直升机在不规则波中的漂浮性能进行分析,以验证文中直升机满足五级海况漂浮稳定性的能力。

选取不规则波的有义波高为4 m,波长为50 m进行验证。根据式(11)的色散关系大致计算得波浪周期为5.65 s,此时不规则波对应的平均风速为13.8 m/s。计算时间选取为10 min,以保证有足够的时间供舱内人员撤离。在初始时刻选取浪向与直升机轴线垂直(浪向90°)与平行(浪向0°)两种状态,以分别验证直升机横倾与纵倾稳定性。

图4给出浪向与直升机轴线平行时直升机俯仰角与横摇角随时间的变化曲线。由于直升机处于迎浪状态,在漂浮过程中直升机的俯仰运动占据主导地位,横摇角几乎不随波浪传递发生变化。直升机在漂浮状态下最大俯仰角可达到30.46°,最大横摇角为0.49°。由于计算直升机的横向重心位置不在纵向对称平面上,因而其横摇运动的平衡位置并非0°。从计算结果可得知,直升机具有较好的纵倾稳定性。

图4 浪向0°直升机姿态角曲线

图5给出浪向与直升机轴线垂直时直升机俯仰角与横摇角随时间变化曲线,此时直升机的横摇运动占主导地位。直升机在漂浮过程中的最大俯仰角为8.06°,最大横摇角为25.1°。由于在10 min内直升机最大横摇角远小于上文计算的稳性消失角52°,故认为该例直升机具有五级海况稳定漂浮的能力。

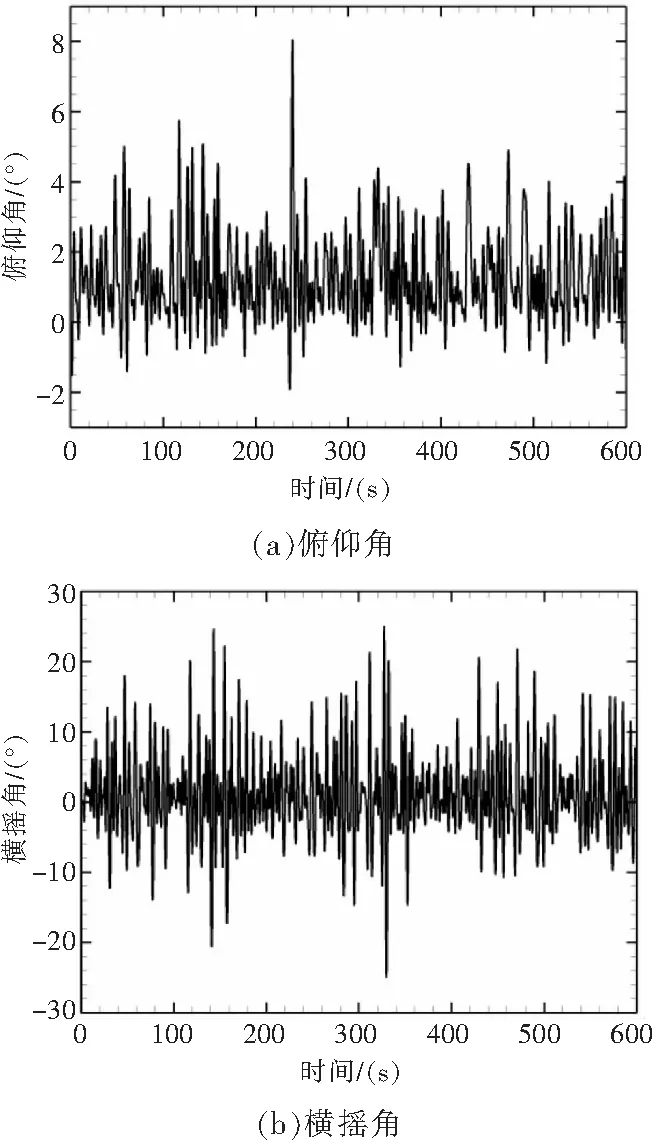
图5 浪向90°直升机姿态角曲线

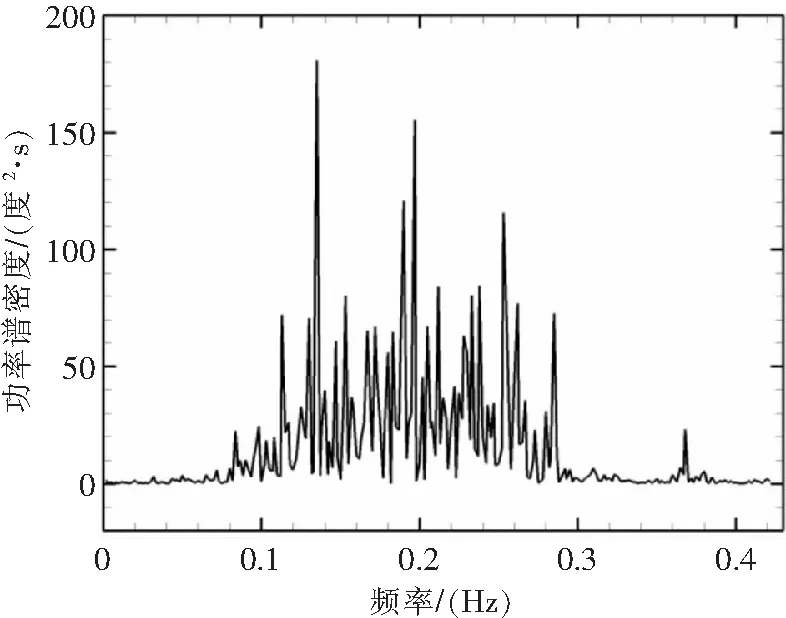
图6 直升机横摇运动功率谱密度

对于浪向90°中的直升机横摇运动进行谱密度分析,可以发现大致有三个能量相对集中分布的区域。第一个区域频率范围为0.08～0.10 Hz。该频率范围对应直升机受二阶波浪力作用引起的低频运动,该区域对于直升机横摇运动影响相对较小。第二个区域频率范围为0.10～0.22 Hz。从图2可知,该频率范围对应波浪能量相对集中的区域,说明在此范围内直升机的横摇为受一阶波浪力作用而产生的波频运动。第三个区域频率范围为0.22～0.40 Hz。该频率范围段接近于直升机的固有频率,直升机受二阶波浪力的影响在横摇方向产生谐振运动,但由于该范围内波浪能量相对较小,该谐振并非直升机横摇运动的主导因素。综合上述分析,直升机的横摇运动主要特征为波频运动,具体体现为直升机的横摇随着波浪的传播而产生相同频率的响应。

2.3 直升机标准海况漂浮能力边界验证

为验证本文2.1节中关于估算直升机漂浮能力边界的方法,需对时域计算下直升机在标准海况中的漂浮稳定性能力边界进行分析。选取波高4.5 m,风速14.8 m/s与波高4.8 m,风速15.2 m/s两种工况进行计算。图7给出了直升机横摇运动随时间的变化曲线。当波高为4.5 m时,直升机在10 min内未发生倾覆;但在555 s时横摇角达到了最大值50.1°,已经接近了直升机的稳性消失角。而当波高为4.8 m时,直升机在165 s便发生了侧倾。上述结果说明算例直升机可承受标准海况波高为4.5 m～4.8 m,与2.1节中通过本文提出的方法计算出的4.5 m基本相符,说明了本文提出关于直升机标准海况漂浮能力边界估算方法的准确性。

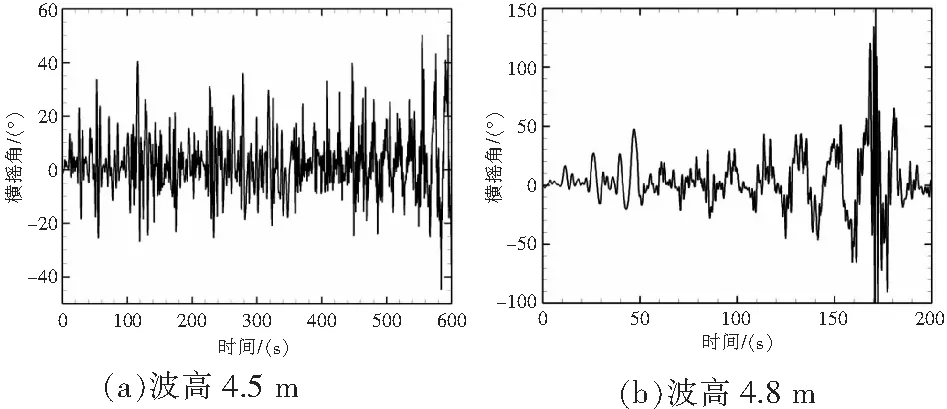
图7 直升机横摇运动曲线

3 结论

本文给出了直升机漂浮能力边界以及抗侧风能力边界的估算方法,并在此基础上给出了直升机的漂浮能力所满足的最大海况。采用基于势流的数值方法对直升机的漂浮能力进行了验证,计算结果表明,本文给出的直升机漂浮能力边界估算方法与数值仿真方法具有良好一致性,可以为后续直升机漂浮系统的设计提供参考。