离子吸附型稀土矿区复垦植被光谱特征变异提取与分析

周贝贝, 李恒凯*, 龙北平

1. 江西理工大学土木与测绘工程学院, 江西 赣州 341000 2. 江西省地质局地理信息工程大队, 江西 南昌 330001

引 言

稀土是我国珍稀战略性资源, 在精确制导武器、 航空航天等诸多尖端军事和高科技领域拥有不可替代的作用。 习近平总书记2019年在江西考察时发表重要指示: “稀土是重要的战略资源, 也是不可再生资源, 要加大科技创新工作力度, 不断提高开发利用的技术水平, 延伸产业链, 提高附加值, 加强项目环境保护, 实现绿色发展、 可持续发展”。 然而长期以来, 稀土矿采用酸性溶液注入矿体的溶浸开采方式, 导致矿区以土壤沙化酸化和重金属污染等环境问题尤为突出, 植被自然恢复过程极其困难, 主要依赖人工复垦[1]。 稀土开采扰动引起的复垦地土壤特殊的物理化学性质变化及稀土开采所导致的环境胁迫, 致使复垦植被长势较差, 已经严重影响了矿区生态安全[2]。 因此获取实时准确的矿区复垦植被数据, 对复垦植被实施动态监测监管, 对矿区生态恢复至关重要。

叶片是反映植被生化组成和健康状况的指标之一, 当植被受到一定程度的环境胁迫时, 其叶片的自身结构发生变化, 致使光谱曲线发生局部异常变化, 能够用来判断植物的生长情况。 对矿区典型植被叶片高光谱特征进行研究, 通过对光谱形状和特征带的生化机理分析可以评价矿区环境胁迫下植被的生长状况。 植被光谱特征分析目前应用于多个方面, Iram M Iqbal等现场收集光谱数据, 使用高光谱指数和叶片光谱对本地和入侵植物物种进行区分[3]; Huang等利用叶片高光谱数据, 通过原始光谱曲线对照, 开发虫害严重程度识别模型-光梯度推进机作为分类器来识别叶片受害程度[4]; Fu等通过自相关函数一阶导数比值差法提取玉米特征, 识别并区分铜、 铅两类重金属污染应力[5]; Yu等测量叶片化学含量成分, 精细监测退化植被, 评估植物营养状况[6]。 各学者将植被光谱运用于不同场景, 而光谱特征分析, 是其研究的共性基础。 离子吸附型稀土矿区特殊的行业差异性和地域性, 其植被的研究较少; 开采扰动引起的重金属污染等多种胁迫造成复垦植被光谱异常, 为探索引起光谱异常的内在机制, 需要对照正常植被光谱, 为进一步研究奠定基础。

同时, 为了从光谱中获取更多信息, 许多学者选择采用导数、 倒数、 对数等线性方法选择和强化光谱特征。 由于小波变换和傅里叶变换等方法在数据压缩和信号去噪方面的独特优势, 一些学者将其应用于高光谱的特征信息提取[7]。 如黄芝[8]采用Db 5小波函数分解获取小波系数并计算小波分形维数, 通过尺度的变化较好的区分不同胁迫水平下的水稻污染情况; 朱红求[9]等使用微型光谱仪采集光谱信号, 对每个奇异值分量作傅里叶变换, 突显出光谱曲线原始特征。 不同的变换方法应用于提取光谱特征参数, 能有效挖掘出光谱特征, 在实际应用中需要根据具体对象及区域进行选择。

基于上述研究, 以稀土矿区典型植被为研究对象, 通过一阶导数、 离散小波变换和分数阶微分对叶片原始光谱进行处理, 对照矿区复垦植被和正常环境植被在原始光谱以及不同方法处理后的光谱特征差异, 分析植被状况, 探讨稀土矿区复垦植被在环境胁迫下的光谱变化及光谱特征, 针对稀土复垦矿区定量生理参数反演和大尺度快速监测提供技术支持和理论依据。

1 实验部分

1.1 研究区概况

岭北稀土矿区位于江西省赣州市定南县, 面积约213 km2。 该稀土矿持续进行稀土开采30余年, 在长期人工浸溶开采与自然高温多雨的双重作用下, 土壤退化问题突出, 属于国家级水土流失重点预防区。 选取岭北甲子背复垦矿点作为研究区域, 坐标: 115°2′22″-115°3′16″E, 24°58′21″-24°59′15″N, 面积约1.6 km2。 该矿点历经“池浸”、 “堆浸”和“原地浸矿”等多种工艺开采, 遗留大量裸露的尾矿和废弃地。 稀土开采扰动引起的复垦地土壤特殊的物理化学性质变化及稀土开采所导致的环境胁迫, 致使矿区生态恢复进展缓慢。

由于稀土矿区废弃地以土壤沙化酸化及重金属污染为主要表现形式, 复垦植被长势较差, 成活率低, 生态恢复困难。 为此, 其复垦植被应具有易存活、 适应性强等特点。 故选取稀土矿区竹柳、 山茶、 桉树、 松树、 油桐、 红叶石楠6种生存能力强、 耐土壤贫瘠的典型复垦植被作为研究对象, 基于复垦植被在稀土矿区环境胁迫下的光谱特征变化展开研究。

图1 研究区地理位置及概况Fig.1 Location and overview of the study area

1.2 数据获取

于2020年8月14日-15日使用美国ASD (Analytical Spectral Devices) Field Spec4地物光谱仪进行叶片光谱测量, 采样间隔为1.4 nm (350～1 000 nm)和2 nm (1 001～2 500 nm)。 具体时间为11:00-14:00之间, 期间天气晴朗、 无风无云, 植被叶片处于成熟阶段。 选取矿区的竹柳、 山茶、 桉树、 松树、 油桐、 红叶石楠六种复垦植被作为采集对象。 此外, 为获取复垦植被光谱与正常植被光谱的差异, 同时在距离甲子背矿点1km范围正常区域(即未进行稀土开采的区域), 相同环境下根据均匀分布原则进行正常环境生长条件下的叶片光谱采集。

测量时确保样本和参考白板处于同一环境, 仪器探头垂直向下, 与叶片保持垂直, 置于叶片上方。 每隔15 min校准波谱仪, 每个叶片样品测量10次, 取其平均值作为样本光谱反射率。 最终共采集复垦油桐92组、 复垦湿地松87组、 复垦红叶石楠68组、 复垦竹柳92组、 复垦山茶130组、 复垦桉树160组、 正常油桐35组、 正常湿地松36组、 正常红叶石楠33组、 正常竹柳36组、 正常山茶40组、 正常桉树43组。 图2为甲子背矿点复垦植被实地数据采集时拍摄, 该图反映出该矿点复垦植被根细枝稀, 叶片发黄。

图2 复垦植被实地采集Fig.2 Reclaimed vegetation field collection

1.3 数据预处理

野外实测叶片高光谱数据易受土壤环境与人为操作干扰, 特别是在稀土矿区地表大面积裸露的背景下, 光谱数据预处理在光谱分析过程中起着至关重要的作用。 预处理主要包括剔除异常光谱、 去噪和均值。 首先剔除异常光谱, 确定植被光谱曲线, 共剔除复垦植被37组, 正常植被14组。 其次去除噪声间隔, 在野外高光谱数据采集过程中, 植被对水汽和二氧化碳具有很强的吸收带, 对可见光和近红外区植被光谱产生重要影响[10]。 因此, 最终选择350～1 350 nm的光谱波段进行研究, 将1 350 nm以上的波段进行剔除。 最后将所有合格叶片样本光谱数据的均值作为最终光谱反射率。

1.4 植被叶片光谱一阶导数

导数法是高光谱光谱变换中最常用的方法, 表示为原始光谱的变化率。 原始光谱经过一阶导数变换处理, 能够部分消除太阳高度角、 地形等引起的亮度变化。 有针对性的减弱稀土矿区特殊的裸露红壤背景对植被光谱造成的影响, 提升光谱特征区间的对比细腻度, 一阶导数变换公式如式(1)

(1)

式(1)中,D(λi)为一阶导数光谱;R(λi+1)、R(λi)分别为波长λi+1、λi处的反射率; Δλi为两波长距离。

1.5 植被叶片光谱分形维数

一维曲线分形维数可以表示该波形复杂程度, 矿区环境胁迫会导致复垦植被的光谱曲线波形产生特殊变化。 假设有一条不规则形状的光谱曲线I, 用一个长度为ε的尺子来衡量该光谱曲线I的长度。 不考虑光谱曲线上小于ε的不规则部分时, 尺子的测量值为Mε(I), 当ε→0时, 如果对常数c和D有

Mε(I)～cε-D

(2)

则该光谱曲线I的维数为D, 常数c可以看成光谱曲线I的D维长度, 将公式两边取对数得

logMε(I)～logc-Dlogε

(3)

当ε趋于零时, 有

(4)

当计算某条光谱曲线分形维数时, 可以选取ε值的一个恰当范围, 绘制logMε(I)和logε双对数图, 其斜率即为光谱曲线的维数D。

1.6 植被叶片光谱小波变换

离散小波变换(discrete wavelet transformation, DWT)是在一系列离散尺度上对信号进行分析的方法, 凭借多尺度特点和突出细化特征的优点被应用于估算植物叶绿素、 重金属胁迫程度等一系列实际问题[11]。 “Db5”小波函数将植被光谱分解为低频和高频两部分, 低频部分被保留, 高频部分被阈值化, 然后继续在低频的部分进行小波分解, 得到低、 高频部分。 经过多层分解可以将原始信号分解为多个子信号, 分解公式如式(5)

(5)

式(5)中,f(λ)为光谱信号,j为分解层,aj为低频部分,di为高频部分。

1.7 植被叶片光谱傅里叶变换

短时傅里叶变换 (short time Fourier transform, STFT)将难以处理的时域信号转换成易于分析的频域信号。 其基本原理是通过窗函数将光谱曲线切分成许多相等的波长间隔, 用傅里叶变化分析每一个波长间隔, 得到频域信号的变化结果, 将所得结果平铺得到二维的表象, 进而通过分析得到波段上的频率特征, 最后实现光谱曲线空频局域化, 具体公式如式(6)

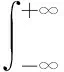
(6)

式(6)中,f(t)为信号函数,g(t-τ)为窗函数,w为信号函数基频率。

此外, 实验通过Specgram函数来实现STFT, Specgram函数的语法如式(7)

[S,F,T,P]=

spectrogram(A, window, noverlap,nfft,fs)

(7)

式(7)中,A为植被光谱曲线; window为窗函数; noverlap为各段之间重叠采样的点数;nfft为计算离散傅里叶变换的点数;fs为采样频率;S为输入A的短时傅里叶变换;F是在输入变量中使用F频率变量;T是频谱图计算的时刻点;P是能量谱密度。

2 结果与讨论

2.1 基于植被叶片原始光谱变异特征分析

获取竹柳、 山茶、 桉树、 松树、 油桐、 红叶石楠的复垦植被和正常植被叶片高光谱数据, 对比复垦植被和正常植被的光谱曲线, 其结果图3所示。

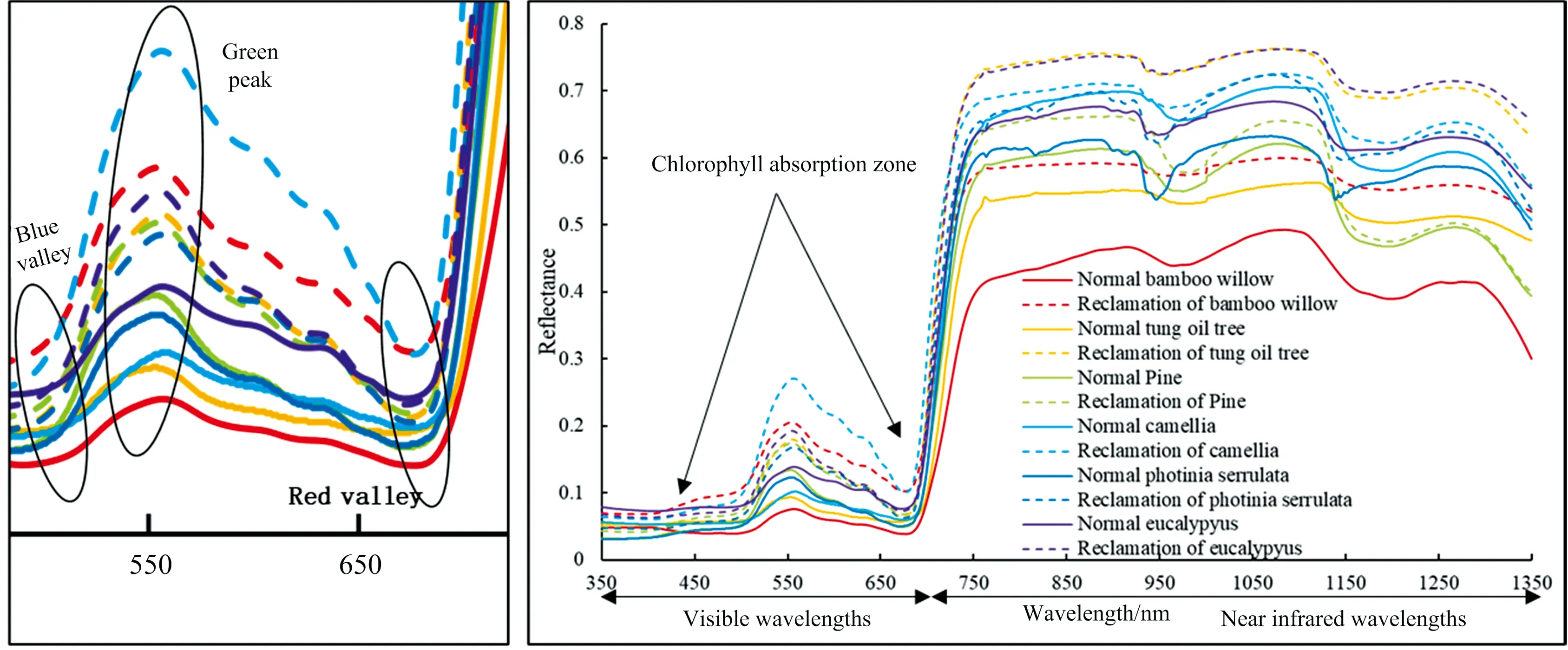
图3 植被原始光谱均值反射率曲线Fig.3 Original mean spectral reflectance curves of vegetation

对照图3中经过预处理的六种复垦植被和正常植被光谱均值反射率曲线, 复垦植被和正常植被的光谱波动趋势基本一致。 400～700 nm(可见光波段), 植被叶片中的叶绿素强烈吸收入射光, 形成”两谷一峰”[450 nm蓝光附近(“蓝谷”)和660 nm红光附近(“红谷”)以及550 nm绿光附近(“绿峰”)], 呈现出区别于其他地物独特的植被光谱特征。 但是无论在可见光还是近红外波段, 矿区复垦植被光谱呈现出相同波长下的反射率均高于其同种正常植被的现象。 有研究证明, 病害程度的增加或者环境胁迫的加剧, 会减少植被叶片叶绿素含量, 而当叶绿素含量降低时, 会导致该光谱区域的叶片反射率增加[12], 这也是矿区环境下复垦植被光谱高于同种正常植被的主要原因。 但正常植被与复垦植被光谱曲线都具备植被基本特征, 虽然存在部分差异, 仅基于原始光谱无法获取丰富的有效信息。

2.2 基于植被叶片一阶导数光谱变异特征分析

导数光谱处理本质上反映了植被中各生理成分的吸收特性, 它可以消除背景噪声的干扰, 并对重叠峰进行分解。 对六种不同胁迫环境下的植被作一阶导数变换, 并根据其光谱特征进行分析。 基于原始光谱一阶导数的植被光谱特征对照结果如图4所示。

植被体内的叶绿素、 含水量和其他物质的光谱吸收, 在可见光和近红外波段形成了“蓝边位置”(490～530 nm最大导数值对应的波长)、 “黄边位置”(560～640 nm最大导数值对应的波长)、 “红边位置”(680～760 nm最大导数值对应的波长)等特征光谱变化相关的区域, 这些光谱特征区域是与植被区别于其他地物的独有性质, 其中应用最多的是“红边位置”。 当植被受到环境胁迫或病虫害等因素的影响时而失绿, “红边位置”将会往短波蓝光的方向偏移(即“蓝移”), 当植被生长旺盛, 生物量高“红边位置”将会往长波红外的方向偏移(即“红移”)[13]。 矿区植被光谱“红边位置”变化情况分别为: 正常竹柳-复垦竹柳(724～718 nm)、 正常油桐-复垦油桐(718～701 nm)、 正常松树-复垦松树(718～718 nm)、 正常山茶-复垦山茶(718～700 nm)、 正常红叶石楠-复垦红叶石楠(719～701 nm)、 正常桉树-复垦桉树(706～701 nm)。 除湿地松外, 大部分植被均出现了“红边位置”的“蓝移”现象, 其中复垦红叶石楠、 油桐和山茶出现了尺度较大的红边“蓝移”。 说明复垦红叶石楠、 复垦油桐和复垦山茶在矿区环境下受到的胁迫较为严重。 掌握了能反映出复垦植被受矿区环境胁迫强弱的信息, 有助于实施针对性治理, 为矿区综合治理提供科学依据。

2.3 基于植被叶片原始光谱分形维数变异特征分析

分形维数通常被用来描述复杂图形的整体特征。 上述的光谱特征参数包括植被指数与“三边”参数(“三边”参数是指基于光谱位置特征的相关变量, 即红边、 蓝边和黄边)都只针对某个波段范围内的光谱曲线, 而部分研究表明地物光谱曲线也具有分形特征[14], 因此引入分形理论综合描述矿区复垦植被和正常植被的光谱差异, 分形维数结果如表1所示。

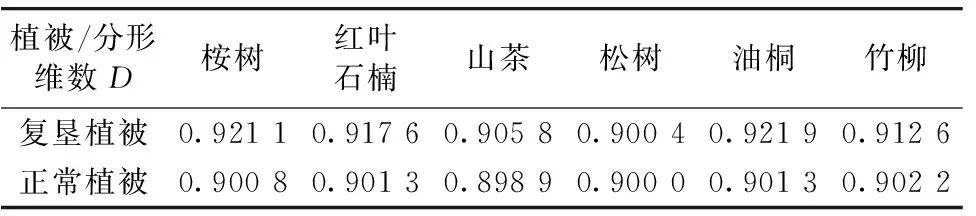
表1 植被分形维数Table 1 Vegetation fractal dimension

通过计算矿区植被光谱曲线的分形维数, 表1中用D表示, 可以看出同种植被在不同生长情况条件下, 呈现出复垦植被分形维数高于正常植被的规律, 其中复垦油桐和正常油桐的分形维数差异最大。 不同于其他光谱参数计算, 分形维数针对全段光谱曲线, 可以综合反映植被光谱总体特征。 根据分形维数的大小一定程度可以判别同种复垦植被与正常植被, 为矿区植被识别与生态恢复提供参考依据。

2.4 基于植被叶片原始和一阶导数的小波变换光谱变异特征分析

用Daubechies小波函数处理样品的光谱曲线, 探测植被光谱在环境下的弱胁迫响应。 将六种植被不同环境胁迫下原始反射以及一阶导数光谱进行离散小波变换, 如图5所示。

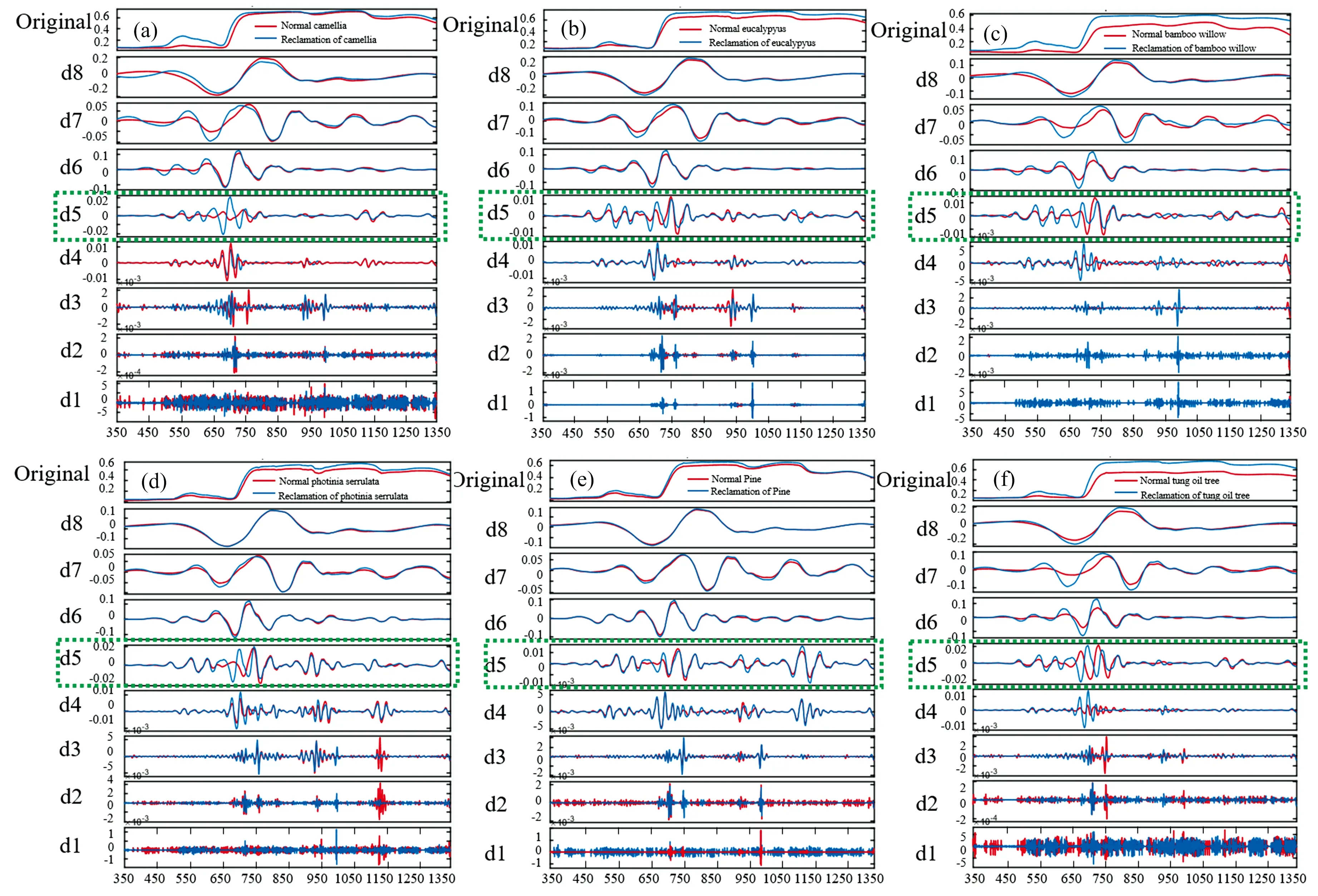
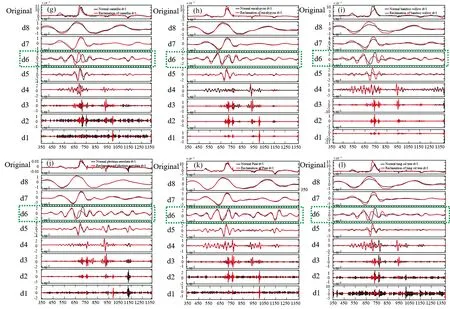
图5 植被原始光谱和一阶导数光谱不同分解尺度离散小波变换波形图(a)-(f): 植被原始光谱小波变换; (g)-(l)为植被一阶导数(dv1)光谱小波变换Fig.5 Discrete wavelet transforms at different decomposition scales for the original and first-derivative spectra of vegetation(a)-(f): The wavelet transforms of the original spectra of vegetation; (g)-(l): The wavelet transforms of first-derivative spectra of vegetation

一维离散小波分解的分解尺度必须为2的整数幂。 如图5所示, 1-8层的分解尺度分别为2、 4、 8、 …、 256 nm, 最终在1-8层产生8个小波细节系数分别为d1-d8。 从d1-d8, 随着分解层数的增加, 呈现出光谱信号频率逐渐降低, 小波细节系数减少, 且小波细节系数对应的光谱特征减弱的趋势。

图5(a)-(f)为植被叶片原始光谱离散小波变换, 在小波细节系数d1-d4范围内噪声较多, 峰谷特征不明显。 从d5开始, 不同环境生长同种植被光谱曲线开始出现明显的差异, 复垦植被和正常植被的峰谷特征在“红边位置”出现交叉。 但小波细节系数d6-d8范围内, 光谱曲线逐渐平滑, 极值交叉点越来越少, 所包含的信息也就越少。 最终原始光谱离散小波换最佳细节系数为d5。

图5(g)-(l)为植被叶片一阶导数光谱离散小波变换, 不同于原始光谱离散小波变换, 在小波细节系数d1-d5范围内存在较多的噪声, 直到d6复垦植被和正常植被在“红边位置”才出现明显的峰谷特征位置交叉现象。 小波细节系数d7-d8范围内光谱曲线的奇异性开始减弱, 特征点开始减少, 最佳细节系数为d6。

与原始光谱离散小波变换相比, 在光谱特征数量相近的情况下, 一阶导数光谱离散小波变换在更小的尺度下放大了光谱特征细节差异, 取得更好的效果。 叶片光谱离散小波变换有利于在多尺度上放大光谱细节特征, 对植被在矿区环境胁迫下的特征为矿区植被生长准确监测提供理论依据。

2.5 基于植被叶片原始和一阶导数的短时傅里叶变换光谱变异特征分析

短时傅里叶变换(STFT)又称窗口傅里叶变换, 短时傅里叶变换可以全面把握光谱回波的信号, 将空间域和频域结合起来, 通过空频分析同时分析光谱信号在空间和频率的变化情况, 将一维植被光谱曲线转换成二维傅里叶图像, 矿区六种植被叶片原始和一阶导数的短时傅里叶变换光谱如图6所示。

如图6所示, 我们将矿区复垦植被和正常的原始光谱以及一阶导数光谱进行短时傅里叶变换, 短时傅里叶变换在空间域将光谱信号截取为多段, 对每一段光谱信号做傅里叶变换, 并计算出频率特性, 继而组合完成空间-频率域的二维图像(空频图)。 经过STFT处理后的光谱信号具有空间域和频域的局部化特征。

在图6(a)-(f)为植被叶片原始光谱短时傅里叶变换, 各原始植被光谱曲线所对应频谱图具有随波长增加其功率谱下降的趋势, 全波段内波形起伏转折较多, 主要集中在350～750 nm(可见光-近红外波段)。 这些空频特征基本都出现在植被原始光谱的“红边”(700～750 nm)与中红外第一个“波谷”(900～1 000 nm)处, 这两个位置光谱反射率相近, 但是通过短时傅里叶变换, 在空频图上实现局域化, 突出了“红边”与中红外第一个“波谷”处的空频特征, 放大了复垦植被与正常植被的特征差异。

在图6(g)-(l)为植被叶片一阶导数光谱短时傅里叶变换, 各植被一阶导数光谱曲线所对应频谱图较原始光谱波形变化在全波段内更加剧烈。 其空频图整体波长归一化频率高于原始植被光谱, 并且出现了更多的空频特征波段。 一阶导数光谱经过短时傅里叶变换后, 整体空频特征波段增加, 同时可以观察到波长归一化频率的变化幅度也更大。 一阶导数在更小的尺度上, 更多的波段放大并增加了空频特征, 对于环境胁迫下的矿区植被识别与特征分析提供依据。

3 结 论

研究和分析了岭北稀土矿区六种典型复垦植被及其对应正常环境植被叶片高光谱数据, 并且将原始光谱进行一阶导数、 离散小波变换、 短时傅里叶变换以及分形维数计算, 主要得到以下结论: (1)一阶导数变换后“红边位置”上复垦红叶石楠、 油桐和山茶的光谱曲线出现了尺度较大的 “蓝移”现象。 (2)计算矿区植被光谱曲线的分形维数, 得到同种复垦植被分形维数高于正常植被的规律。 (3)植被叶片光谱经过离散小波变换, 原始光谱离散小波变换最佳细节系数为d5, 一阶导数光谱离散小波变换最佳细节系数为d6。 (4)光谱通过短时傅里叶变换在空频图上实现局域化, 原始光谱空频特征出现在“红边”与中红外第一个“波谷”处, 而一阶导数短时傅里叶变换在更小的尺度上, 更多的波段放大并增加了光谱曲线空频特征。 以上实验结果表明, 将信号处理方法运用在光谱处理能够较好的提取矿区植被光谱变异特征, 达到我们通过对比复垦植被与正常植被光谱曲线, 间接监测矿区生态环境恢复的目的。 稀土是重要的战略资源, 也是不可再生资源, 加强项目环境保护, 实现可持续发展刻不容缓。 研究结论为准确实现矿区大面积高光谱遥感监测提供理论依据, 为矿区生态恢复重建提供技术支持。 不足在于本研究从叶片尺度进行特征提取和分析, 一定程度上缺少对空间尺度的关注。 在后续的研究中可以加强对多空间尺度的关注, 加强地面实测复垦植被数据与无人机数据、 卫星数据等多尺度之间的关系研究。