基于正交试验的光声池气流性能模拟及参数优化

程 刚, 曹亚南, 田 兴, 曹 渊, 刘 锟

1. 安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室, 安徽 淮南 232001 2. 中国科学院安徽光学精密机械研究所, 安徽 合肥 230031

引 言

利用光声光谱原理实现对气体浓度的检测是光声技术中最为典型的应用。 与其他光谱类气体检测方法相比, 光声光谱气体检测技术主要有结构简单、 探测器不受波长的限制、 零背景噪声、 成本低等优点, 在气体检测领域已得到了广泛的认同与应用。 光声池作为光声光谱气体检测系统中最为核心的部件, 其性能的优劣直接对系统检测结果产生重要影响, 因而对光声池开展优化成为了该领域研究的热点。 在光声池性能优化方面, 国内外学者进行了大量的研究, 取得了许多有益的结论和结果。 Kost等通过数值模拟获得了一种由多个轴对称锥体连续连接形状的光声池结构[1]; Haouari等采用声学三维拓扑数值计算与平滑处理技术获得了一种形如“土豆”结构形状的光声池[2]; Mikael等从圆柱腔圆柱面开设腔, 并采用计算流体动力学分析了光声池的流致噪声[3]; Cheng等提出一种声强得到增益的“喇叭口”形状及阶梯复合形光声池[4-5]; Zhang等设计出一种高灵敏度的椭球形共振光声池[6]; Li等设计了一种母线为双曲线的曲体束腰型光声池结构方案[7]; Liu设计了一种“T”型光声池[8]; Shi等、 Zhao等及Jiao等对球形光声池的性能开展相关研究[9-11]; Zhao等设计了一种拱形光声池, 并确定了其最佳结构尺寸[12]; Yu等设计并试验了一款基于耦合积分球光声池的在线气体检测装置[13]; Yin等设计了具有两个相同谐振器的差分式光声池[14]; Ma等提出一种利用棱镜作用实现多通道反射增强型光声池[15]。 通过优化光声池的结构, 上述研究取得了良好的预期效果, 为光声光谱气体检测性能的提升以及光声池的结构创新设计提供了大量的技术支持和参考。 然而, 上述大多数研究主要是在系统的静态条件下进行的, 光声光谱在线检测系统中光声池中气体流动性能和动态时间响应等方面研究报道较少, 这无疑构成了进一步提高光声光谱检测性能的障碍。 因此, 在前人研究的基础上, 探索动态条件下的光声池参数影响规律与优化组合进而提高光声池的检测性能具有重要意义。

基于三维流场数值模拟方法, 建立了光声池流场的稳态和瞬态模拟模型, 重点研究了光声池腔内气体流动过程引起的动态压力效应和时间响应, 利用正交试验设计和熵权法分析了光声池参数的影响规律, 通过对指标的权重平衡, 提出了光声池的最佳参数组合, 相关结论可为光声池的后续扩展和优化研究提供借鉴。

1 计算模型与三维流场模拟

1.1 计算模型

用于光声光谱气体检测的圆柱形光声池结构示意图与实物如图1所示。 光声池与待测气体接触的内腔部分主要包括光声池Z轴向腔内正中间的圆柱形谐振腔和其两端的圆柱形缓冲腔, 以及壳体的表面对称开设有进、 出气孔形成的孔腔。 当光声池处于动态检测过程中时, 被测气体的流动路径是从进气孔流向靠近进口孔的缓冲腔, 然后沿着谐振腔流向靠近出气孔的缓冲腔, 最后从出气孔流出。 现有的光声池结构原始尺寸为: 光声池壳体总长L=220 mm, 其Z轴端面为正方形, 尺寸a×a=100 mm×100 mm; 谐振腔半径Rre=5 mm, 长度Lre=100 mm; 缓冲腔半径Rbuff=35 mm, 长度Lbuff=60 mm; 进、 出气孔半径Rin=Rin=5 mm, 进、 出气孔中心距离Ljc=170 mm。 光声池三维流场计算物理模型是光声室腔内形成的封闭气体区域。

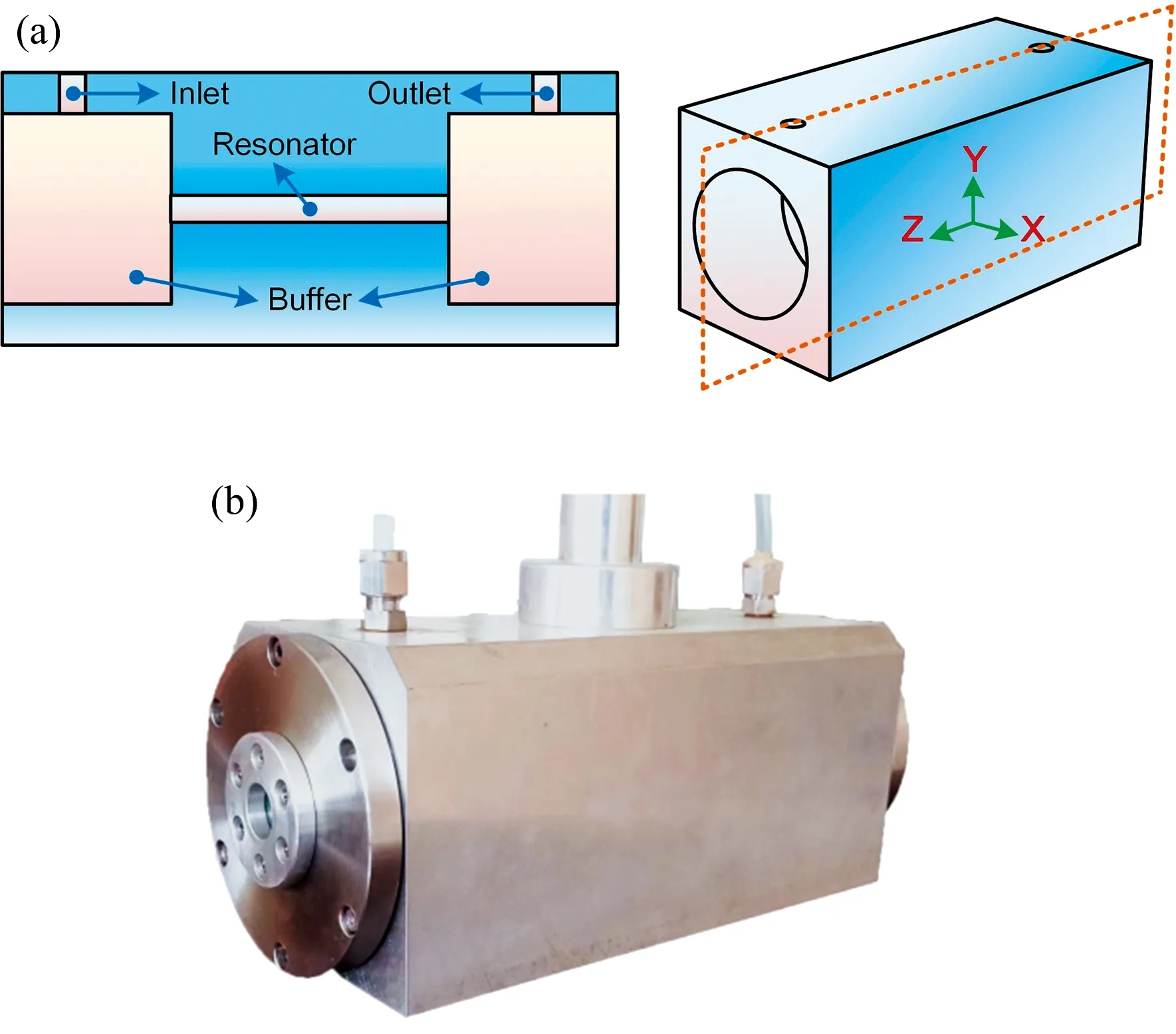
图1 光声池结构模型图(a): 模型图; (b): 实物图Fig.1 Structure diagram of photoacoustic cell(a) Model diagram; (b): Physical photos

1.2 控制方程

光声池腔内气体流场模拟采用计算流体动力学(computational fluid dynamics, CFD)方法, 腔内气体流动需要遵循流场基本控制方程的约束。 因不涉及热量交换, 所以控制方程主要由质量守恒方程、 动量守恒方程组成, CFD计算均以上述方程为基础。 在笛卡尔坐标系中可写出对应的气体控制方程通用形式如式(1)[16]

(1)

式(1)中,φ为通用变量,Γ为广义扩散系数,S为广义源项。

其质量守恒方程为

(2)

式(2)中,ρ为流体密度,u为速度矢量,t为时间。 式(2)是瞬态三维可压流体的质量守恒方程, 若流体视为不可压, 式(2)可变为

(3)

其动量守恒方程为

(4)

式(4)中,μ为流体的动力粘度,Su、Sv、Sw为动量守恒方程中的广义源项。

1.3 基本假设与边界条件

抽取光声室腔内形成的封闭气体区域为流体求解域。 采用稳态和瞬态流场模拟开展计算, 基本假设如下: ①简化光声池的细节结构, 忽略腔内的小凸台、 小凹槽等几何模型细节特征, 不考虑因机械加工带来的结构误差; ②腔内气体视为理想性气体, 为不可压缩流体介质, 且不考虑湿度影响; ③视腔内表面为理想光滑表面, 不考虑腔内粗糙度对气流的影响。

边界条件: ①腔内气压初始状态为0.1MPa, 介质为空气, 体积分数为100%, 通入气体为纯甲烷气体, 体积分数为100%; ②进气孔处边界设为气流速度入口,uin=0.06～0.10 m·s-1, 并设置为“充分发展流动”, 出气孔处边界设为压力出口, 为0.1 MPa, 考虑气体产生的重力影响; ③腔内温度恒定为293 K, 腔内壁面为绝热无滑移边界; ④腔内气流动态压力模拟设置为CFD稳态计算, 腔内气体浓度调节时间模拟设置为CFD瞬态计算, 设定模拟时间t=300 s, 计算步长为3 s。

1.4 网格独立性验证

网格划分对计算收敛值具有重要影响, 其精细度也决定着计算机运算时间。 验证网格独立性可以在计算精度和时间之间达成折衷。 设置计算模型网格划分为三维自动划分, 最小缝隙尺寸为2 mm, 每次运算均提高初始网格的精度级别。 模型网格计算图如图2所示, 谐振腔、 进气口、 出气口以及过渡处均进行网格自动加密, 整个模型采用了结构化网格进行处理。 设定uin=0.06 m·s-1, 计算目标为谐振腔轴线中点处动压值Pj0, 其随网格数量变化的影响规律如图3所示, 当网格数量在分别在42万和14万左右时, 谐振腔轴线中点处动压值Pj0变化率仅为3.7%, 趋于稳定状态, 继续增加网格数量对结果影响不明显, 因而综合确定光声池流场模拟计算时的网格精度初始级别为6级, 网格数量为14万左右。

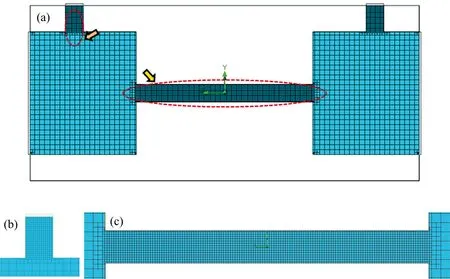
图2 计算网格图(a): 整体网格图; (b): 进气孔处网格图; (c): 谐振腔与过渡处网格图Fig.2 Calculation grid diagram(a): Overall grid diagram; (b): Grid diagram at air inlet hole; (c): Grid diagram of resonator and transition

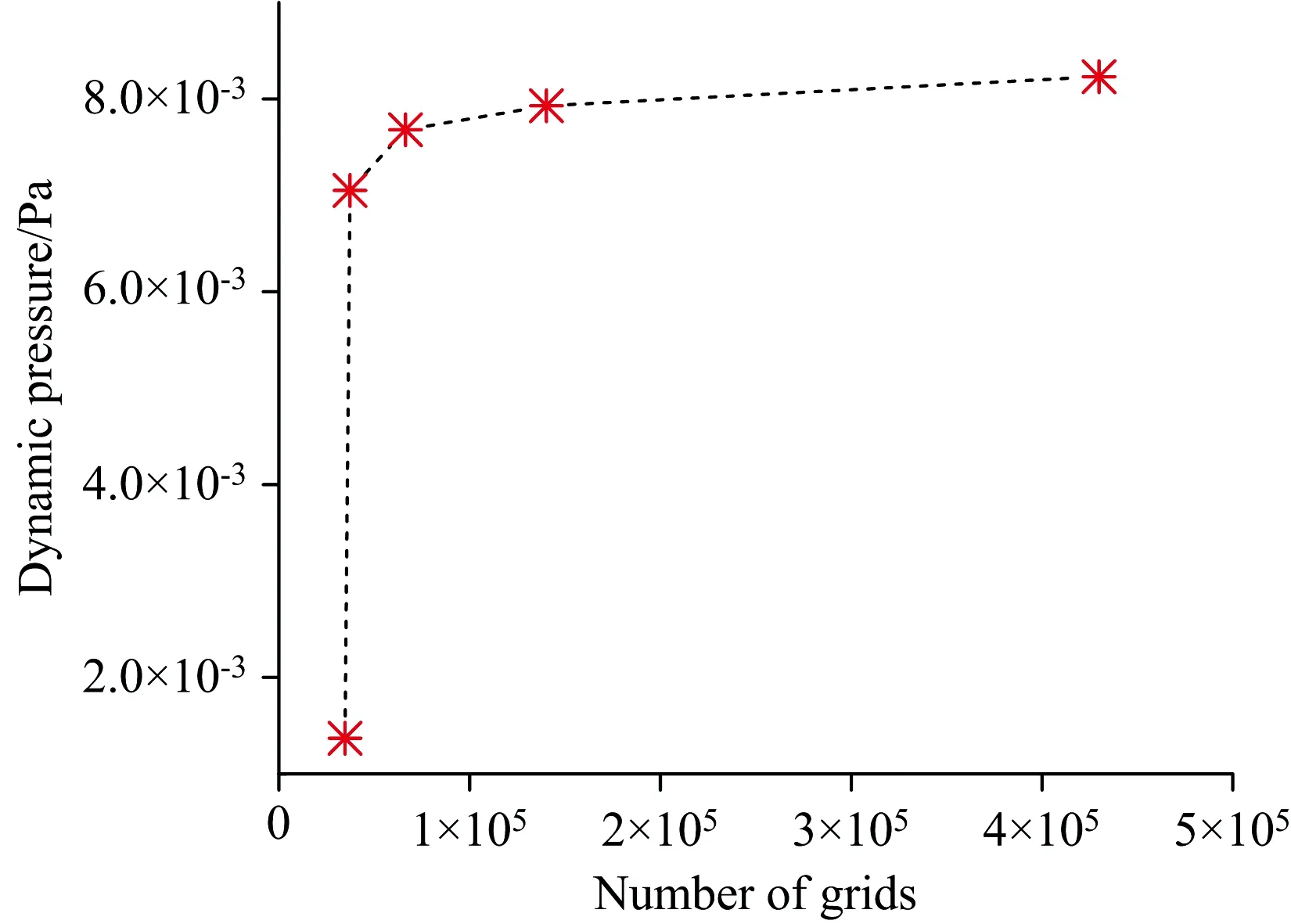
图3 网格独立性验证Fig.3 Grid independence verification

1.5 模拟结果

1.5.1 稳态模拟

模拟求解稳态条件下光声池纵向对称截面的流场分布如图4所示, 可知光声池腔内进、 出气孔以及谐振腔处的动压值过大。 过大的动压会引起较强的气流扰动, 从而增加信号检测噪声, 特别是谐振腔轴线中部的动压波动会直接对声学传感器的检测造成负面影响; 此外, 从图4中还可以看出, 光声池两端缓冲腔中存在气流涡旋现象, 这也会增强流体噪声影响。

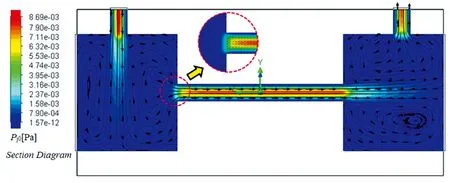
图4 腔内动压与流线分布切面图Fig.4 Section diagram of dynamic pressure and streamline distribution in the cavity

模拟计算进气速度uin分别为0.06、 0.08和0.10 m·s-1时, 谐振腔轴线上动压分布规律, 如图5所示, 可知谐振腔轴线上动压大小随着进气速度uin的增大而增大, 由文献[3, 17]可知, 流速越大腔内涡旋回流将会越大, 导致的气体噪声越强, 因而动压与流速可以等同地表征气体的扰动影响。 气体从缓冲腔流进和流出谐振腔时动压波动较为明显, 且气流进入谐振腔时的动压变化梯度强于气体流出谐振腔时的动压变化梯度, 但在谐振腔中动压表现的相对平稳, 上述是由于腔体截面直径的突扩和突缩流体局部阻力变化引起的。 因此可以预见, 减少腔内气流流速及优化光声池中的过渡结构将会改善气流引发的动压波动程度。

图5 不同进气速度下谐振腔轴线动压值分布Fig.5 Dynamic pressure distribution at the axis of the resonator at different inlet speeds

1.5.2 瞬态模拟

模拟求解瞬态条件下光声池腔内待测气体变化规律如图6所示, 调节时间t设定为当光声池中甲烷气体体积占比到达并保持在稳态值的c=95%所需的最短时间, 探测点设置为谐振腔轴线的中点。 由图6可知, 在不同的进气速度下, 腔内气体的体积比例随着时间的增加而增加, 并逐渐达到稳定的状态, 在早期, 腔体中待测气体的体积比例增长速度较快, 在后期, 其增长速度逐渐减慢。uin为0.06、 0.08、 0.10 m·s-1时, 调节时间t模拟结果分别为171、 132和108 s, 这是由于气体流速增大时, 待测气体在腔内的扩散速度将随之增大, 因此可以预见, 提高腔内的气体流动速度可以缩短调节时间, 这与实际也非常吻合, 进而提高系统检测的动态响应速度。 结合稳定模拟的动压结果可知, 腔内气流流速将是光声池内动压波动与动态响应的重要影响参量。

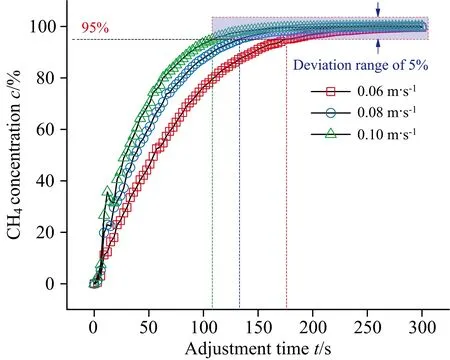
图6 光声池腔内气体浓度调节时间Fig.6 Adjustment time vs gas concentration in photoacoustic cell cavity

2 结构方案设计

通过对光声池腔内流场的模拟分析可知, 腔内的动压、 浓度调节时间与流速及结构突变等因素密切相关, 因此改善光声池的内腔结构具有重要意义。 为充分利用现有的光声池, 最大限度减少其加工成本, 在不改变原光声池主体结构的情况下, 采用模块化设计策略, 如图7所示, 具体如下: ①将光声池壳体沿缓冲腔的轴线并按其直径尺寸将其加工成通孔; ②将原谐振腔结构改为谐振腔组件, 谐振腔组件为独立圆柱体结构, 其外径大小与缓冲腔相同, 谐振腔组件可沿Z轴进行移动, 处于中间位置时, 光声池Z轴两端可以自然形成缓冲腔; ③根据流场模拟结果及文献[17]可知, 对腔体截面突变处进行适当过渡处理可以进一步提高气流局部阻力变化; ④为进一步改善谐振腔中的气体流速的平稳性, 在谐振腔组件上沿Z轴尝试开设均匀分布的辅助孔。

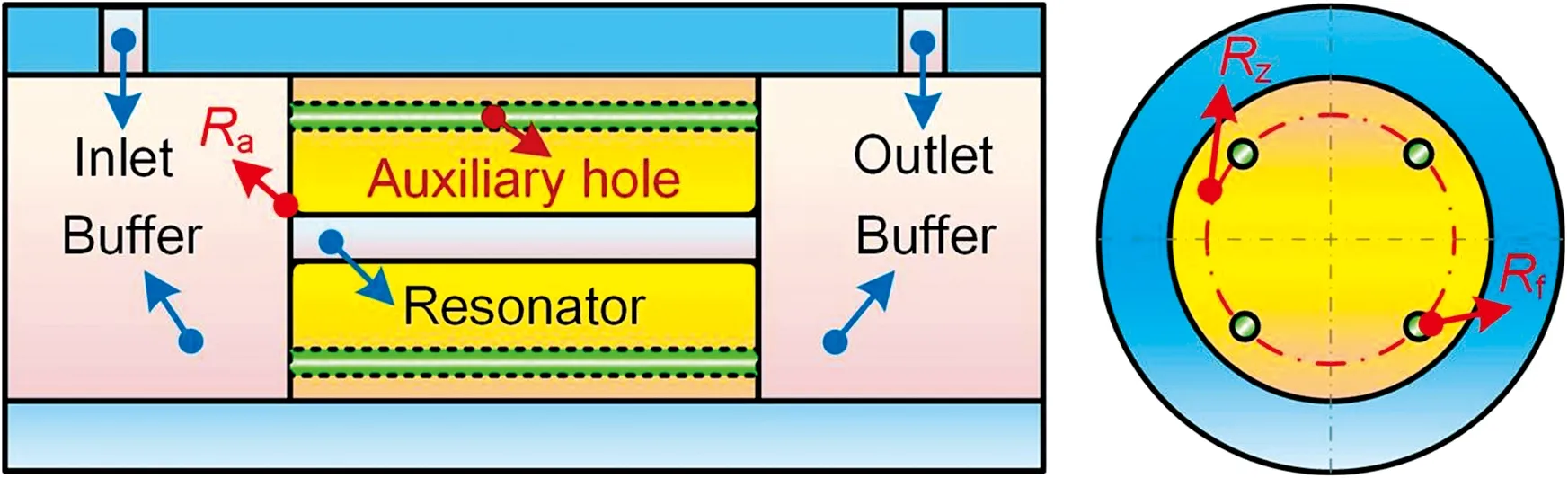
图7 光声池结构改进方案示意图Fig.7 Schematic diagram of structural improvement scheme of photoacoustic cell

3 正交试验分析

3.1 试验方案与计算

正交试验是利用数理统计学和正交性原理开展合理试验的一种科学方法, 特别适合研究和处理多因素优化分析。 采用正交试验的方法对光声池的结构改进参数开展研究。 将缓冲腔与谐振腔过渡处圆角Ra(A)(2.0～5.0 mm)、 辅助孔数量为Nf(B) (2～8个)、 辅助孔半径Rf(C)(2.5～4.0 mm)、 辅助孔中心圆半径Rz(D)(20.0～27.5 mm)以及进气速度uin(E)(0.06～0.08 m·s-1)5个参数选为考察因素, 每个因素取4个水平, 其他参数保持不变, 不考虑因素之间的交互影响, 以谐振腔轴线中点处动压值Pj0、 腔内气体浓度调节时间t为试验评价指标, 因素-水平表如表1所示。

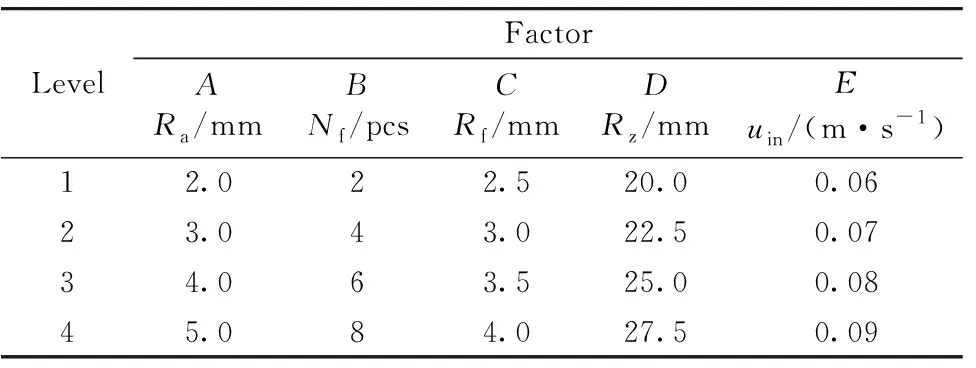
表1 因素-水平表Table 1 Factor level table

采用正交表L16(45)安排试验, 需要开展16次试验, 试验方案及计算如表2所示。

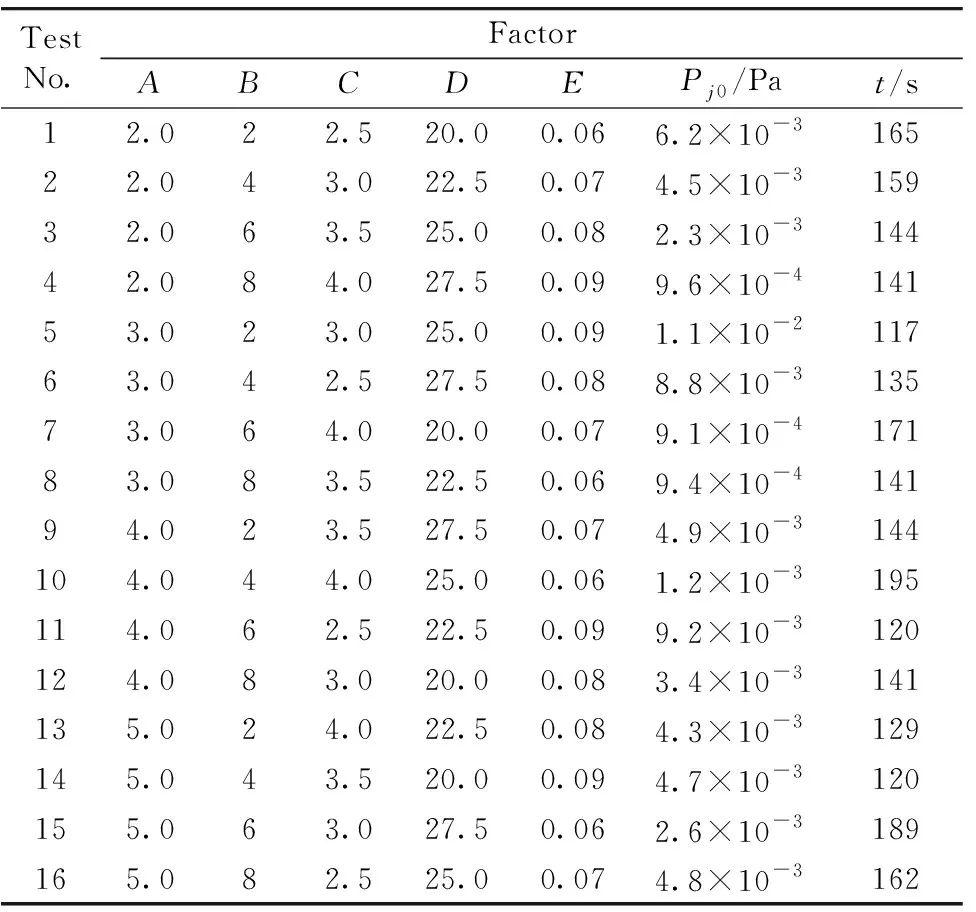
表2 试验方案及计算结果Table 2 Test scheme and calculation results

3.2 极差分析

试验条件下的均值与极差计算结果如表3所示, 从试验结果中可直观看出, 第7组试验组合A2B3C4D1E2中动压值Pj0最小, 此时Pj0=9.1×10-4Pa, 调节时间t=171 s; 第5组试验组合A2B1C2D3E4中调节时间t最小, 此时Pj0=1.1×10-2Pa, 调节时间t=117 s。 极差R表示各个因素对指标结果的影响程度,R=max(k1,k2,k3,k4)-min(k1,k2,k3,k4),kj为第j列同一水平试验结果的平均值, 极差R越大, 表明该因素对试验结果影响越大, 其重要性越强。 从表3极差结果可知, 光声池的各参数对动压值Pj0影响的主次顺序为: 辅助孔半径C>辅助孔数B>进气速度E>过渡圆角A>辅助孔中心圆半径D, 且各因素的影响程度区分度不大; 各参数对调节时间t影响的主次顺序依次为: 进气速度E>辅助孔半径C>辅助孔数B=辅助孔中心圆半径D>过渡圆角A, 且进气速度远高于其他因素对调节时间的影响。

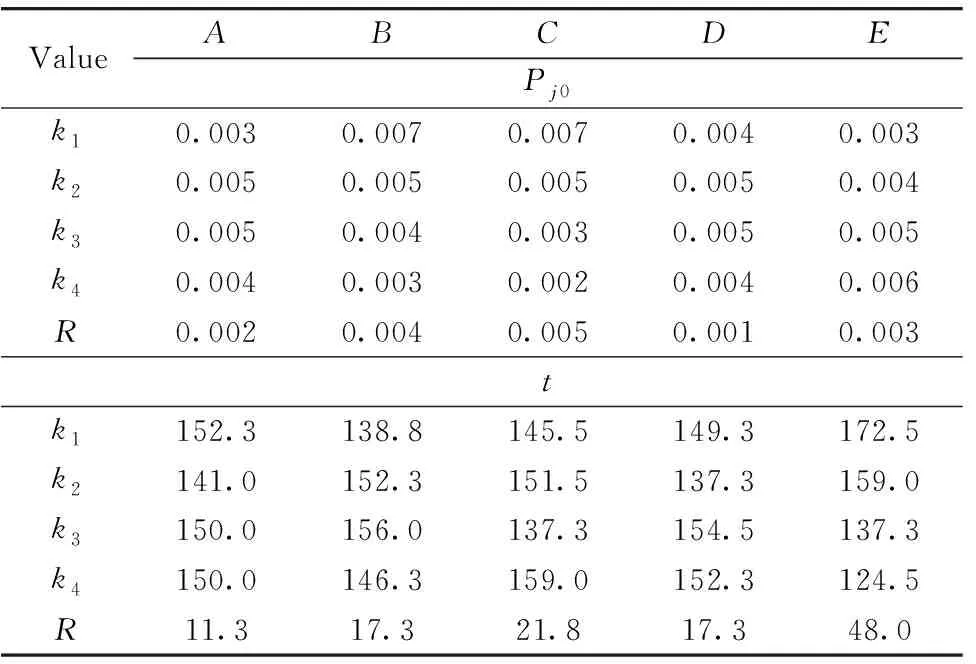
表3 均值与极差Table 3 Mean and range

动压值Pj0和调节时间t均期望越小越好, 因而选取因素水平应该取使指标小的水平。 在所做试验的范围内, 仅考虑动压值Pj0时, 光声池的结构参数最优组合为A1B4C4D1E1&A1B4C4D4E1, 上述参数组合在正交试验中未出现, 通过仿真计算获得此时Pj0=4.6×10-4Pa &Pj0=4.6×10-4Pa, 调节时间t=216 s &225 s; 仅考虑调节时间t时, 光声池的结构参数最优组合为A2B1C3D2E4, 此时Pj0=8.0×10-3Pa, 调节时间t=114 s。 上述结果表明, 通过正交试验极差的分析, 在参数试验范围内可实现光声池最佳的动压值和调节时间的参数组合, 显示了所采用正交试验的优越性和可行性。

3.3 熵权法及最优参数组合

光声池的最优参数组合需要同时考虑动压值和调节时间2个评价指标, 属于多目标参数优化, 同时两者为望小特征。 从上述正交试验中可知, 动压值和调节时间两者是互相冲突的, 即不能同时取到两者的最小值。 为兼顾两个指标的影响, 找到最佳指标下的参数组合, 需将多目标参数优化问题转化成单目标优化问题。 常见的方法采用单目标权重法来进行处理, 为客观地给出动压值和调节时间的权重, 采用熵权法建立评价模型, 利用信息熵计算两者的权重。 数据分析对象为正交试验中的16组试验计算结果。 同时, 将正交试验中仅考虑动压值或调节时间的计算结果作为补充数据, 共有19组Pj0&t指标数据, 补充数据如表4所示。

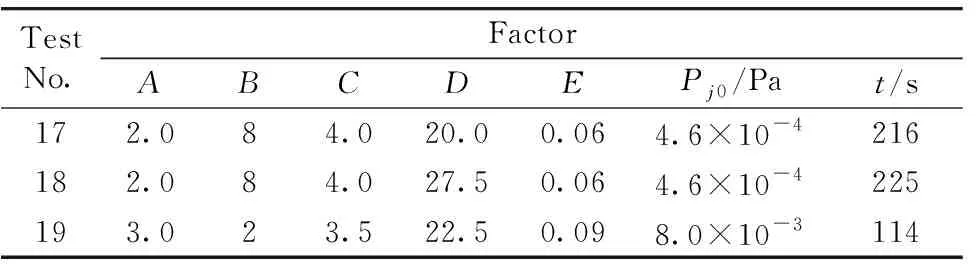
表4 补充数据Table 4 Supplementary data

由于动压值和调节时间两者的量纲不同, 需对19组Pj0&t数据进行标准化处理, 因两者均为负向指标, 标准化公式如式(7)[18]

(7)

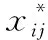
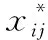
(8)

Pj0&t的信息熵eij计算公式如式(9)

(9)

Pj0&t的信息熵ωij计算公式如式(10)

(10)

数据集中每个方案的综合评价得分si计算方式如式(11), 综合评价得分的值越大越好。

(11)

动压值和调节时间权重计算结果如表5所示。

表5 熵权法计算结果Table 5 Calculation results of entropy weight method

由表5可知, 在试验范围内, 从客观角度可知光声池调节时间的权重略大于动压值的权重。 结合式(11)可计算出19组Pj0&t指标数据的综合评价得分前3组的依次为第8组、 第4组、 第14组,s8=0.849,s4=0.848,s14=0.774。 根据以上分析, 并结合光声池制作成本及实际需求等, 可以合理选择其参数组合, 选择综合评分最高的第8组参数组合为其最优参数组合。

3.4 优化方案对比

设定其进气速度uin均为0.06 m·s-1, 对比光声池优化前后的结果。 图8为第8组参数组合下的腔内动压与流线分布切面图, 结合图4可知, 优化前后的光声池腔内最大流速基本保持不变, 优化后的腔体中的流速更加均匀、 平滑, 腔体中的动压大幅降低。 圆角的处理使得谐振腔两端处的腔体截面直径的突扩和突缩引起的动态变化变得更加缓和, 同时, 出气孔端的缓冲腔内的气流涡旋现象也得到了改善。 图9优化后腔内球状粒子流线图, 可知光声池腔内气体均匀地从辅助孔通道中分散流动, 以致气流在谐振腔中更加低速、 平滑地流动, 如此可以降低光声池腔内的气流扰动噪声, 从而最终改善光声池的信号检测噪声。

图8 优化后腔内动压与流线分布切面图Fig.8 Section diagram of dynamic pressure distribution and streamline distribution in optimized cavity

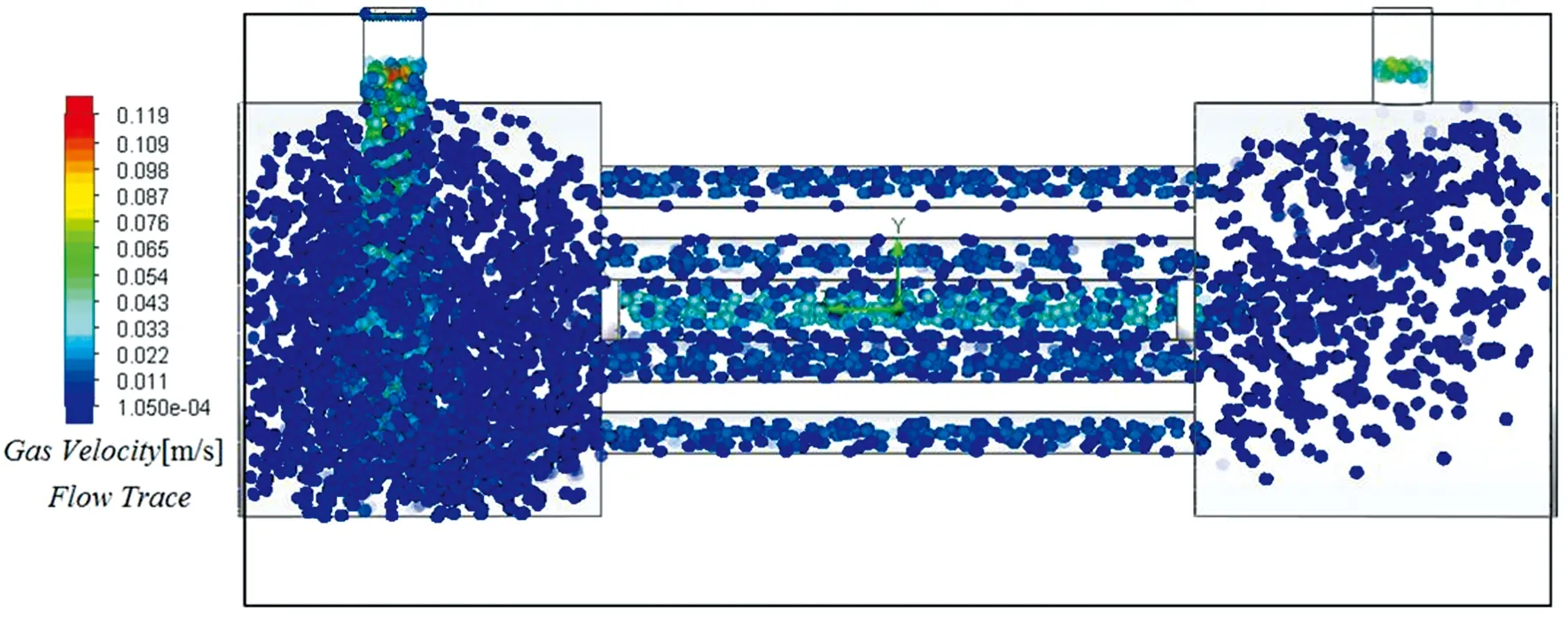
图9 优化后腔内球状粒子流线图Fig.9 Streamline diagram of spherical particles in cavity after optimization

图10为光声池优化前后振腔轴线中点处动压值Pj0、 腔内气体浓度调节时间t两个指标的结果对比图, 可知优化后的动压值Pj0为9.4×10-4Pa, 调节时间t为141s, 相较于优化前的指标, 动压值相对降低了88.1%, 调节时间相对降低了17.5%, 两项评价指标均得到优化提升, 优化效果较为理想。

图10 优化前后结果对比Fig.10 Comparison of results before and after optimization

4 结 论

(1)基于三维流场数值模拟方法, 建立了光声池流场的稳态和瞬态模拟模型, 计算并获得了光声池腔内气体流场分布及其气体浓度平衡响应情况和规律。 结果表明, 降低腔内气流流速、 优化光声池中的过渡结构可改善气流引发的动压波动程度以及缩短调节时间;

(2)运用正交试验设计与熵权法, 研究了光声池结构参数对谐振腔轴线中点处动压值和气体浓度调节时间的影响规律。 在研究参数范围内, 获得了其最佳参数组合为: 缓冲腔与谐振腔过渡处圆角为3.0 mm、 辅助孔数量为8个、 辅助孔半径为3.5 mm、 辅助孔中心圆半径为22.5 mm、 进气速度为0.06 m·s-1;

(3)优化后的光声池谐振腔轴线中点处动压值为9.4×10-4Pa, 腔内气体浓度调节时间为141 s, 相较于优化前的指标, 动压值相对降低了88.1%, 调节时间相对降低了17.5%。