四向穿梭车仓储系统复合作业调度优化

许丽丽，詹燕，鲁建厦，郎一丁

(1.浙江工业大学 机械工程学院，浙江 杭州 310032；2.宁波富佳实业股份有限公司，浙江 宁波 330200)

在土地成本不断上升的背景下，为了降低仓库成本，四向穿梭车（以下简称四向车）仓储系统因其密集程度高、可低楼层存储、灵活性好等优势，被广泛应用于家电、烟草和超市等领域.该系统主要由四向车和提升机协同作业，实现跨层和跨巷道的运输，一台四向车配合提升机就能到达仓库任意储位.当系统物流量增加时，可通过增加四向车的数量来满足出入库需求，应用灵活方便.在实际运行中，四向车系统存在堵塞问题，这主要与货架上的四向车水平通道和垂直提升机的设置有关.特别在四向车系统的复合作业调度中，须对订单任务进行排序，规划四向车的作业路径，并考虑四向车和提升机的协同作业方式，这增加了四向车系统调度的复杂性.因此，如何对四向车系统进行调度优化成为亟须解决的问题.

目前，国内外学者对仓储系统调度问题的研究主要包括路径规划、货位优化、订单排序等问题[1].Roy 等[2]研究四向车系统中驻点位置以及交叉通道位置，指出不同位置的选择对拣选效率的影响.Ekren[3]以最小化平均周期时间和平均能耗为目标确定四向车系统的物理结构设计.针对多层穿梭车仓储系统，Wang 等[4]研究该系统的拣选作业问题，Carlo 等[5]研究2 台提升机下多巷道的系统，建立以出入库作业时间最短为目标的数学模型，确定2 台提升机的作业顺序.汤洪涛等[6]对跨层跨巷道穿梭车仓储系统的复合作业路径进行优化.

在单一作业的研究中，刘刚等[7]针对多层穿梭车系统研究穿梭车和提升机并行工作的约束机制，以出库时间最小为优化目标建立数学模型，并提出Gurobi 与启发式算法结合的方法求解，提高系统作业效率.何昕杰等[8]为了缩短双深位四向车系统的出库作业时间对订单进行排序，并采用改进的遗传算法求解.因单一作业在实际应用中效率低，采用复合作业更符合仓库实际作业模式.

在复合作业的研究中，占翔南等[9]针对多深度的四向车系统，在水平方向解决了多台四向车在同层作业时造成的冲突死锁问题.张经天等[10]针对四向车系统的提升机设计调度策略，构建垂直方向的提升机作业的数学模型.在不同设备之间协同作业的研究中，周亚勤等[11]建立有轨车和穿梭车之间的协同作业模型和多出入库任务的多设备作业调度模型.目前对四向车系统复合作业调度优化的研究主要集中于垂直或水平方向，对两者协同作业的研究较少.然而，在实际应用中，对该作业的调度问题不可避免，因此须进行相关研究.

调度问题属于多项式复杂程度的非确定性多项式（non-deterministic polynomial，NP）难问题，使用精确算法求解效率低，而使用智能优化算法可快速求解该问题[12-13].为了改进经典遗传算法求解调度问题容易陷入局部最优这一缺点，隋振等[14]针对四向车系统处理多订单任务的问题，提出自适应遗传退火算法对系统的作业时间模型求解.季顺松等[15]设计剪枝的改进遗传算法，提高算法收敛精度.对改进遗传算法在解决调度问题上的研究表明，对遗传算法进行改进可有效弥补遗传算法容易陷入局部最优的不足.

本研究基于四向车在水平方向上的作业特点，通过增设横向轨道设计四向车系统，使系统在不进行移库和占地面积小的情况下能够存储多种类型的物料.考虑到提升机与四向车复合作业的特点，进行水平和垂直方向上的建模，并采用基于任务分类的遗传算法设计，以最小化作业时间为目标对模型进行求解.

1 系统概述

1.1 系统描述

如图1 所示为某四向车系统示意图.平面示意图如图1（a）所示，采用贯通式货架存储，每四排货架为一组，组与组之间由纵向轨道隔开，每组货架两端及货架的列方向均可存储不同类型货物.每组货架底部为四向车运动轨道，采用四向车对托盘进行存取，四向车沿货架横向、横向轨道及纵向轨道运动.立面示意图如图1（b）所示，采用提升机作为四向车垂直方向上的转运设备，位于横向和（或）纵向轨道端点，图1 中提升机位于横向轨道左端，货架存储的第1 层与提升机相交处为托盘在系统中的出入口，即I/O 口.输送线位于I/O 口旁边，用于托盘的进出转运.四向车搭乘提升机在垂直方向运动，在I/O 口实现出入库.传统穿梭车系统的货架对称排列在巷道两侧，每个巷道都配备提升机和穿梭车，这种系统结构单一，不适用于不规则的场地.而本研究所采用的系统允许提升机设置在货架的横向和纵向轨道两端，这增加了系统适用的场景多样性，同时还能根据出入库数量的增加来增加四向车和提升机，以提高系统的运行效率.

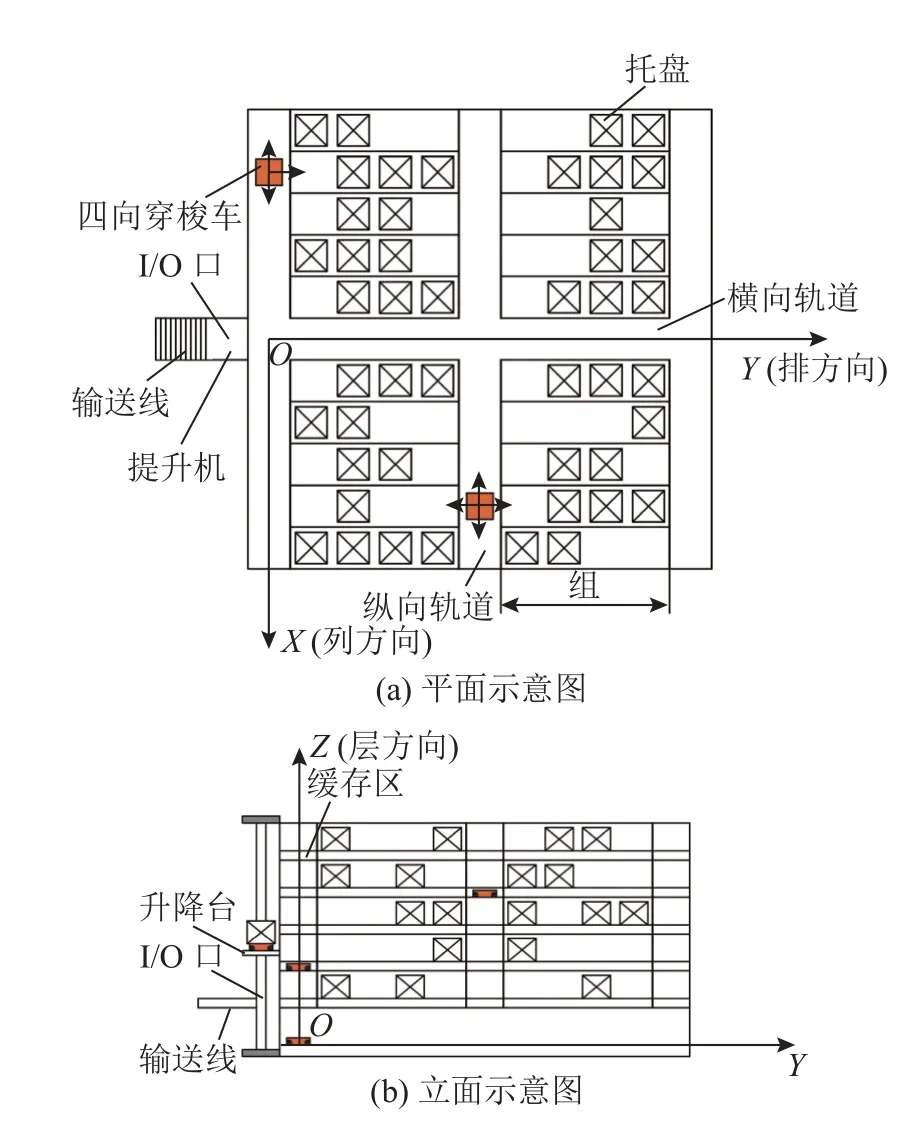
图1 四向穿梭车仓储系统示意图Fig.1 Diagram of four-way shuttle warehouse system

1.2 作业流程

四向车系统设备作业方式包含单一作业和复合作业：1）单一作业，提升机配合四向车从I/O 点出发一次只完成入库或者出库任务后再回到I/O 点；2）复合作业，提升机配合四向车从I/O 点出发完成入库后再完成出库任务回到I/O 点.当复合作业中某一作业货位在I/O 点时为该作业下的单一作业，故仅介绍复合作业的作业流程.将一次复合作业划分为入库、空载和出库作业，作业流程如图2 所示.在垂直方向上，提升机从货架底层完成一次复合作业到达第1 层的路径如图2（a）所示；在水平方向上，四向车从缓存区到目标货位A 路径如图2（b）所示.图中，红色路径为路径1，绿色路径为路径2，记J为路径，J=1 时为路径1，J=2 时为路径2.系统完成一次复合作业的流程如下.

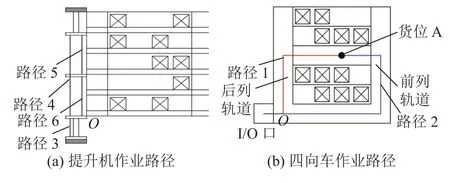
图2 四向车系统复合作业路径示意图Fig.2 Schematic diagram of compound operation path of four-way vehicle system

1）入库作业：四向车移动至提升机内，提升机沿路径3 从货架底层运动至第1 层，随后从输送线传送托盘至四向车上，再由提升机沿路径4装载满载的四向车至入库任务所在层，四向车离开提升机后完成提升机的入库作业，最后由四向车装载托盘运送至对应入库货位并释放，完成四向车的入库作业.其中，若该货位与后列轨道之间没有托盘，四向车将沿路径1 至入库货位；反之，四向车将沿路径2 至入库货位.

2）空载作业：在完成入库作业后，提升机和四向车处于空载状态.当入库任务与出库任务货位在同一层时，四向车将以最短路径从入库货位到达出库货位完成空载作业，该情况下不需要提升机，其空载时间为0；当入库任务与出库任务货位在不同层时，四向车将沿路径1 至该层缓存区等待提升机空闲，再由提升机移动至四向车所在层，随后四向车搭乘提升机沿路径5 至出库任务所在层，四向车离开提升机后，提升机完成空载作业，四向车沿路径1 至出库货位完成空载作业.

3）出库作业：四向车在出库货位上取出托盘后，将其运送至该层的缓存区等待提升机的空闲.若出库货位和后列轨道之间没有托盘，四向车将托盘装载，并沿路径1 运送至缓存区；若出库货位和后列轨道之间已经有托盘，四向车将按路径2将托盘运送至缓存区.如果入库货位与出库货位位于同一层，则四向车将搭乘提升机沿路径4运送至货架的1 层.反之，如果入库货位与出库货位不在同一层，则四向车将搭乘提升机沿路径6运送至货架的1 层.在到达货架1 层后，释放托盘到输送线上，从而完成提升机和四向车的出库作业.此外，如果任务已完成，四向车搭乘提升机沿路径3 前往底层并释放，四向车停靠在底层；如果任务尚未完成，则将继续执行任务.

2 系统建模

为了对四向车系统建模，建立如图1 所示坐标轴.任务task 在货架中的坐标为(x(task),y(task),z(task))：x(task) 为任务task 所在列，当x(task)＜0时，货位在横向轨道的上方，当x(task)＞0 时，货位在横向轨道的下方；y(task) 为任务task 所在排；z(task)为任务task 所在层.

2.1 问题描述

四向车系统通过提升机和四向车的协同作业实现托盘的出入库.在提升机将四向车运送至目标任务层后，为了减少设备作业等待时间，四向车在水平方向运动时，提升机可根据其他四向车的作业情况对其作业进行分配.将系统中的任务分配给提升机和四向车执行，以横向轨道左端的提升机为例，构建在该提升机下的数学模型，并将四向车和提升机完成一次复合作业划分为入库、空载和出库作业进行研究.其调度问题的数学描述如下：系统有一台提升机和m台四向车，须完成n个出/入库任务，作业次数为3n次，四向车作业集合B={B1,B2,···,Bm}，四向车集合S={s1,s2,···,sm},第i台四向车的作业集合Bi=E为第i台四向车的作业次数，提升机的作业集合A={a1,a2,···,a3n}.type 为与aj的作业类型，与aj/3 的余数为1 时为入库作业；余数为2 时为空载作业；余数为0 时为出库作业.在满足约束条件下，合理安排四向车和提升机的任务分配及任务的执行顺序.约束条件构建如下：

式（1）表示每台四向车至少分配一个作业；式（2）表示四向车将执行所有任务；式（3）表示一个任务只能由一台四向车执行；式（4）表示提升机将执行所有任务；式（5）表示每个任务仅由一辆提升机完成一次.

2.2 系统假设

针对四向车系统复合作业调度问题，建立以作业时间最短为目标的模型.为了简化研究对象，对系统进行如下假设：

1）初始状态时升降台和四向车均在货架底层；

2）四向车一次只运送一个托盘；

3）提升机一次只运送一台四向车；

4）提升机设置在横向轨道左端；

5）每台四向车完成该层任务后在缓存区等待提升机空闲；

6）四向车和提升机均匀速行驶；

7）货物出入库位置已知.

2.3 水平方向建模

在四向车系统中，当四向车载着货物从提升机上驶出到达任务所在层的缓存区后，四向车在水平方向行驶到达任务所在储位，完成任务后返回缓存区，等待提升机空闲后载着该四向车完成后续任务.四向车从缓存区O到提升机I/O 点的时间ts=w/vx，w为单个货格宽度，vx为四向车的运行速度.对于一次出入库任务所划分的入库、空载、出库作业，记系统中一次复合作业的入库任务为u，坐标为 (x(u),y(u),z(u))，出库任务为v，坐标为 (x(v),y(v),z(v))，对四向车在水平方向的作业建模.

1）入库作业，即四向车从该层缓存区处出发到达入库所在货位，其行驶距离表达式为

式中：d(Oz(u),u)为四向车从点Oz(u)到点u的行驶距离，Oz(u)表示任务u所在层的缓存区点位；mod(y(u),5)为y(u) 除以5 的余数；l为单个货格的长度.

2）空载作业，即四向车从入库货位到达出库货位，其行驶路径分为2 种情况：z(u)=z(v)

a）出入库货位位于同一层，即.

四向车从入库货位到出库货位行驶路径如图3 所示，其距离表达式为

图3 四向车在 z (u)=z(v) 时完成空载作业路径图Fig.3 Diagram of idle load operation path completed by four-way shuttle underz(u)=z(v)

当 α=1 时，

b）出入库货位位于不同层，即z(u)≠z(v).

将四向车的空载作业行驶路径分为2 部分：四向车从入库货位出发到达该层缓存区的行驶距离d(u,Oz(u))，此时四向车须等待提升机空闲，然后将四向车运送到出库货位所在层，四向车再运动至该层缓存区；四向车从出库缓存区出发到达出库货位行驶距离d(Oz(v),v).表达分别如下：

3）出库作业，即四向车从出库货位出发到达该层缓存区，其行驶距离表达式为

2.4 垂直方向建模

当系统完成任务时，提升机先完成每台四向车的第1 个入库作业，则a1～am均为入库作业，且作业对象分别为四向车完成的，p(a1)=1，p(a2)～p(am) 的值分别为a2～am对应入库作业所在层.提升机am+1～a3n的作业与四向车完成作业时间、作业类型和四向车位置有关，对其讨论如下.

1）提升机完成的aj为入库作业（t ype(aj)=1，j＞m）.

若提升机完成的aj为入库作业，则提升机完成的aj-1为出库作业，且该作业完成后依旧由四向车i完成入库作业，因此提升机完成作业aj后不一定继续由同一辆四向车完成aj+1,且该作业类型未知.提升机完成aj-1作业后位于系统第1 层，则

式中：to为提升机从传送带搂取或释放托盘时间，h为单个货格的高度，vz为提升机在垂直方向上的运行速度.

式中：tl为四向车举起或释放托盘时间.

2）提升机完成的aj为空载作业（t ype(aj)=2，j＞m）.

由于提升机完成的aj为空载作业，同时四向车i完成的空载作业，而提升机前一次完成的作业为空载作业或入库作业，此时提升机开始aj作业所在层则为完成aj-1作业所在层，即

将该空载作业分为2 种情况进行讨论：

3）提升机完成的aj为出库作业（t ype(aj)=0，j＞m）.

提升机完成一次出库作业后下一作业为入库作业，因此aj-1不为出库作业，故而该作业结束后提升机所在层为z(aj-1)，即

综上所述，采用一台提升机时完成n个出入库任务所需时间为

上述水平方向和垂直方向的模型均基于一台位于横向轨道左端的提升机而构建，对于系统中存在2 台提升机且另一台位于横向轨道右端时，须在水平方向建模时以该提升机处缓存区的坐标进行构建，并对提升机进行选取.为了减少系统作业时间，选择距目标货位行驶时间更短的提升机.记横向轨道右端提升机位置，即该处的出入口为 I′/O′.如图4 所示，目标货位C距 I′/O′的行驶距离更近，其时间更短，此时该任务由右端提升机完成.在确定行驶距离时须考虑该任务的属性（入库或出库）以及货架的状态（空载或满载），其具体方式如2.3 节水平方向作业路径所示.当该提升机须完成的任务数为n′时，完成任务所需时间为

图4 2 台提升机路径示意图Fig.4 Ptah diagram of two elevators

综上所述，当系统完成 (n+n′) 个任务时：若仅使用一台提升机，完成任务时间T=EE(a3(n+n′)) ；若采用2 台提升机，完成任务时间T=max(T1,T2)，为了使系统完成任务时间最短，定义目标函数为

3 算法设计

针对四向车系统复合作业调度问题，先将任务分配给提升机，再根据任务类别分配四向车并随机排序，然后对提升机完成的任务依据调度规则进行排序.此时提升机和四向车均获得初始的任务顺序，为了找到调度问题的优化解，采用基于任务分类的遗传算法进行求解.

3.1 任务调度规则

在系统作业中，基于订单信息、四向车和提升机的工作状态信息以及系统货架存储状态信息对任务进行调度.其中，订单信息包含出入库货位信息和任务紧急程度信息.系统调度须先对任务进行分配再排序，规则如下.

1）任务分配规则.

a）若系统中存在多台提升机，将任务分配给距目标货位行驶距离较近的提升机，按提升机的任务量分配合理台数的四向车.

为了保证完成任务时间最短，应尽量让四向车在完成一次复合作业时的入库货位与出库货位处于同一层，此时四向车空载作业时间减少，提升机的空载作业时间为0，使得任务作业时间减少.因此优先将xc与yc的任务进行匹配，若匹配完成后仍存在任务未完成，再将其与其他任务进行匹配.将任务配对后随机分配给四向车.

2）任务排序规则.

基于分配给提升机的四向车及其随机分配的任务，确定提升机完成任务顺序，排序须遵循以下规则.

a）提升机将所有四向车的第1 次入库作业依次完成后再继续后面的任务，保证四向车均在系统中并已开始作业.

b）提升机优先完成订单紧急作业.

c）提升机选择距离最近的四向车作业.

基于规则a）将四向车输送至系统中，若存在规则b），则优先考虑规则b），否则按规则c）进行排序.

3.2 改进遗传算法设计

作为成熟的随机寻优算法，遗传算法能够较好地解决调度问题，但因其存在局部搜索能力较差的问题须进行改进.所研究的调度问题已将任务进行分类，而基于任务分类对遗传算法的种群初始化有助于找到更优的初始解，提高遗传算法的搜索能力，因此采用改进的遗传算法（improved genetic algorithm，IGA）对文中的调度问题进行求解.对提升机和四向车进行任务分配和初步排序，然后采用IGA 优化作业时间，以单台提升机作业为例，算法流程如图5 所示.

图5 改进遗传算法流程图Fig.5 Flow chart of improved genetic algorithm

1）初始化货架状态.

对四向车系统中货架存储状态进行初始化.在系统中，当四向车对货物进行拣选后，货架上的存储状态发生改变.本研究主要考虑的是对一批订单进行四向车的路径规划，在规划前初始化货架状态，即货位上是否存储货物，若是，记该货架状态为1，否则记为0.

2）种群初始化与编码.

基于3.1 节的任务分配规则将n个出入库任务信息转换成3n个提升机和四向车的作业信息，对出入库任务进行分类，初始化染色体种群，对染色体进行编码，生成长度为3n的染色体，1 ≤r≤n.1 条染色体一共5 层，第1 层为四向车的作业顺序编码，当染色体处于 (3r-2) 位时该作业为入库作业，其值为1～n的随机排列，当染色体处于 (3r-1) 位时该作业为空载作业，其值为(3r-2)位和3r位的组合数，当染色体处于3r位时该作业为出库作业，其值为以规则a）为基础与入库作业匹配后产生的值；第2 层为四向车的编号编码，由于3 个作业由同一辆四向车完成，其值以3 个值为一组，大小为1～m的随机整数；第3 层为提升机的作业顺序编码，其值须根据规则b）、c）及第1、2 层的染色体来决定；第4 层为提升机的作业类型编码，值为1 时为入库作业，值为2 时为空载作业，值为3 时为出库作业；第5 层为提升机对应四向车的编号.在对染色体进行变换的时候，只变换第1、2 层的染色体，后3 层根据规则3、4 用前2 层2 条染色体计算得出.

3）染色体解码.

假设某条染色体如图6 所示，该染色体包含3 次复合作业：入库3 对应出库2；入库1 对应出库3；入库2 对应出库1.提升机载着四向车2 完成入库3，四向车2 继续完成空载作业32，提升机回到底层载着四向车1 完成入库作业1，四向车1继续完成空载作业13，提升机将载着四向车1完成空载作业13，接着四向车1 和提升机完成出库作业3 回到底层，再由提升机和四向车1 完成入库作业2，四向车1 继续完成空载作业21，提升机完成空载作业回到底层，再由提升机和四向车1完成入库作业2，四向车1 继续完成空载作业21，提升机完成空载作业32，接着四向车2 和提升机完成出库作业2 回到底层，四向车2 任务结束，提升机继续完成空载作业21，接着四向车1 和提升机完成出库作业1 回到底层完成所有作业.

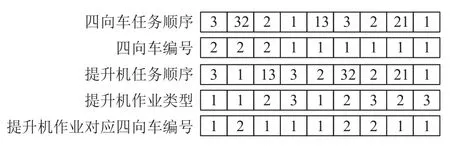
图6 染色体示例Fig.6 Chromosome Examples

4）适应度函数计算.

以系统完成任务的时间最短为目标，将该目标作为适应度，在进行计算时须考虑系统完成一次复合作业后货架状态再计算下一次复合作业的时间.适应度函数为

5）选择.

在进行选择交叉变异时，仅对染色体的第1、2 层进行操作，第3～5 层根据前2 层的值进行计算.在选择父代时，由于染色体之间适应度的方差较大，最大值大于最小值的一倍，不宜采用轮盘赌的方式进行选择，故而采取精英选择加随机选择的方式，进行交叉变异产生新的子代.首先进行精英选择，将每一代种群中适应度在前10%的个体挑选进入下一代种群，然后用随机选择的方法进行每个个体的挑选，按照选择概率确定每个个体是否被选择作为父代.

6）交叉.

在交叉操作时，在满足规则a）的情况下，生成一个1～Tier 的随机数i，将父代第1 层染色体1 在xi与yi中的值与父代第1 层染色体2 中xi或yi进行随机交叉，再随机生成一个1 或3 的值，若产生的值为1，则对入库作业编号进行交叉，若产生的值为3，则出库作业进行交叉，即完成同层任务之间的交叉操作，其他染色体不变，生成子代染色体.假设产生的层数为2，对入库作业进行交叉操作，x2={3,5,7}，染色体第1 层的交叉过程如图7所示.在对染色体第2 层交叉操作时，将父代1 中入库作业为3、5、7 对应的四向车编号随机与父代2中入库作业为3、5、7 对应的四向车编号交叉操作.

图7 第1 层染色体交叉操作示意图Fig.7 Schematic diagram of chromosome crossing operation in first layer

为了增加个体多样性，提高搜索效率，采用自适应交叉算子和变异算子，自适应交叉算子表达式为

式中：f=max (ft,ft+1)，t为迭代次数，f为迭代t次时种群适应度的平均值；fmax、fmin分别为f的最大值、最小值；Pc,max，Pc,min分别为交叉算子最大值和最小值，Pc,max=0.8，Pc,min=0.5；ρ=Pc,max-Pc,min[16].

7）变异.

在变异操作时，随机产生2 个1～n的随机数r1和r2，再随机产生一个1 或3 的值，若产生的值为1，则对入库作业编号进行变异，即位数为(3r1-2)和 (3r2-2)；若产生的值为3，则出库作业进行编号，即位数为3r1和 3r2.将对应父代染色体第1 层相应的作业顺序进行交换，第2 层将 (3r1-2)、(3r1-1)、3r1对应的四向车编号与 (3r2-2)、(3r2-1)、3r2对应的四向车编号进行交换.自适应变异算子表达式为

式中：Pm,max、Pm,min分别为变异算子最大值、最小值，Pm,max=0.05，Pm,min=0.001；η=Pm,max-Pm,min[16].

8）判断是否终止算法.

若迭代次数小于或等于最大迭代次数，返回步骤2），继续迭代；若迭代次数大于最大迭代次数，则输出最优解.

4 实例分析

为了对IGA 进行评价并验证该算法的可行性和有效性，以某四向车系统为例，采用MATLAB2016b 软件对四向车系统的调度优化问题进行实例分析.对系统和算法设置参数如下：货架排、列、层数分别为10、20 和5；货格的长、宽、高分别为1.0、1.0、0.8 m；四向车在水平面上运动速度为3 m/s；提升机的运动速度为2 m/s；提升机搂取或释放托盘的时间为3 s；四向车从缓存区到提升机的时间为0.33 s；四向车举起或释放托盘的时间为3.00 s；算法的种群大小为100；迭代次数为1 000；四向车搬运成本c1=10 元/s；仓库使用成本c2=50 元/s；提升机搬运成本c3=15 元/s；四向车使用成本c4=800 元/台；提升机使用成本c5=3 000 元/台.

4.1 实例验证

为了对研究问题进行实例验证，选取四向车系统执行复合作业20 次，即入库任务20 次，出库任务20 次，分别由1、2、3、4 台四向车和一台位于横向轨道左端的提升机完成，具体出入库任务如表1 所示.表中，加粗标记的任务须在任务开始后40 s 内完成.初始化仓库货架状态，如表2 所示的货位为装载货位，其他为空闲货位（入库货位应为空闲货位，出库货位应为装载货位）.

表1 出入库任务列表Tab.1 Inbound and outbound tasks list

表2 初始状态下的装载货位Tab.2 Loading position under initial status

基于货架初始状态以及订单信息，采用IGA 对该任务进行排序和分配，对四向车台数分别为1、2、3、4 台的系统完成任务.一般而言，若不考虑提升机，仅对四向车的任务进行分配，则四向车台数越多，完成效率越高.但由于只考虑一台提升机，且存在提升机和四向车的任务分配及提升机和四向车之间的协同作业，会降低四向车的利用率.随着四向车台数的增加，提升机的等待时间也会增加.通过IGA 对研究问题进行求解，每种情况分别运行30 次取平均值，其结果如表3 所示.表中，TZ 为四向车的作业时间，TW 为四向车的等待时间，TM 为提升机的运动时间，TC 为总任务完成时间.系统中四向车台数越多，完成任务时间越短.

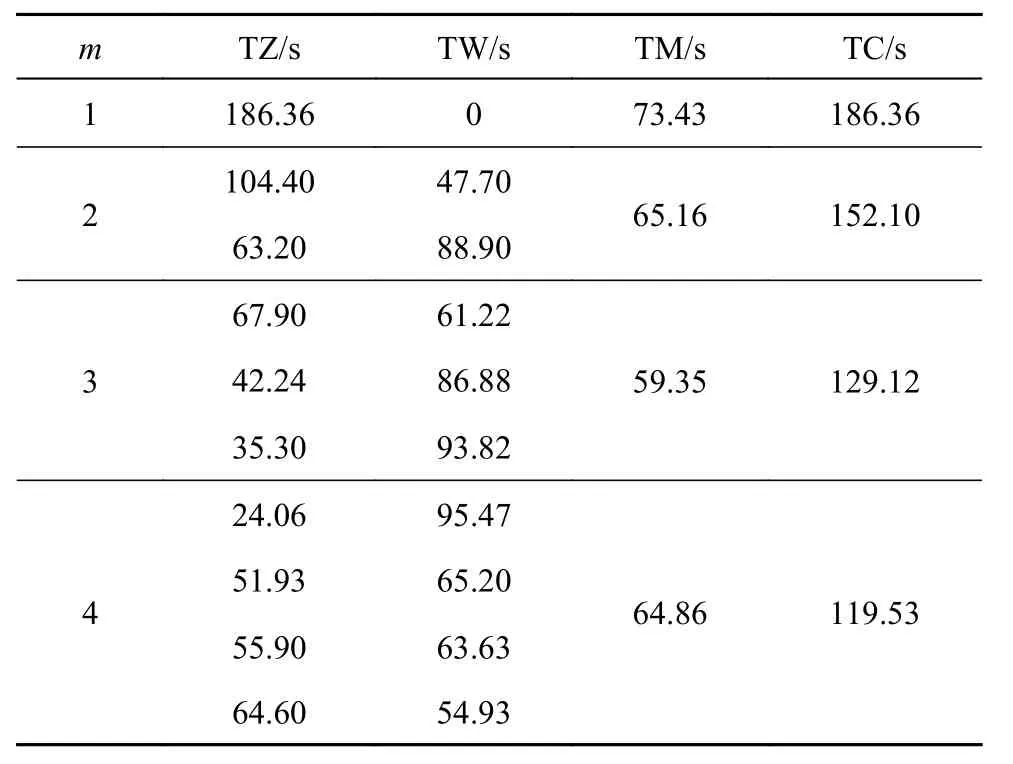
表3 不同四向车台数下IGA 优化的系统作业时间Tab.3 System operation time of IGA optimization under different number of four-way shuttle

为了确定四向车台数，对系统成本的计算如下：

式中：t1为四向车的作业时间，t2为仓库的使用时间，t3为提升机的运动时间.由于已考虑提升机的使用成本，提升机等待状态下的成本忽略不计.根据表3 求出的设备作业时间，可以计算出系统成本和各设备成本，如图8 所示.可以看出，随着台数的增加，四向车花费成本逐渐增加；提升机花费成本基本持平，在四向车台数为3 时成本最少；仓库使用成本随着四向车台数的增加而减少；系统成本在四向车台数为3 时取得最小值.综上所述，系统成本的变化主要取决于四向车和仓库使用成本，在该实例中，为了使系统完成任务花费成本最少，应采用3 台四向车，此时四向车完成任务顺序如表4 所示.提升机的作业顺序可以根据四向车的作业顺序及系统的调度规则进行计算.

表4 四向车台数为3 时的作业顺序Tab.4 Sequence under number of four-way vehicles of three

图8 不同四向车台数下的成本Fig.8 Cost under different numbers of four-way shuttles

上述实例采用IGA 对复合作业为20 次的任务进行优化，未体现该算法在研究该问题上的性能，因此须对算法性能进行分析.

4.2 算法性能分析

为了对算法性能进行分析，在系统中采用一台四向车和一辆提升机完成订单，并在不同订单规模下对IGA 与GA 的优化结果进行比较，优化后所需的订单时间如表5 所示.表中，no为订单数，AVE 为算法求解的任务平均完成时间，δ 为算法优化效率，VAR 为算法求解的方差，δ=(AVE(GA)-AVE(IGA))/AVE(GA).其结果显示当订单规模增大时，δ 呈现上升的趋势，意味着IGA 所优化的结果更好.IGA求解的方差也小于GA 的，效率至少提高了10.3%.算法在订单数为500 时的算法迭代图如图9 所示.IGA 在迭代到582 代时达到优化解，而GA 在822 代时才达到.为了进一步对IGA的性能进行分析，分别采用IGA 和GA 对单双台提升机在订单数为200 时不同四向车台数下的任务完成时间进行比较，其结果如图10 所示.可以看出，在同一任务下采用IGA 优化后的任务完成时间均明显比GA 的时间短，而且在系统采用2 台提升机时所优化的结果更明显.因此，相较于GA，IGA 具有更高的效率和鲁棒性.

表5 不同订单规模下算法优化结果Tab.5 Algorithm optimization results under different order sizes

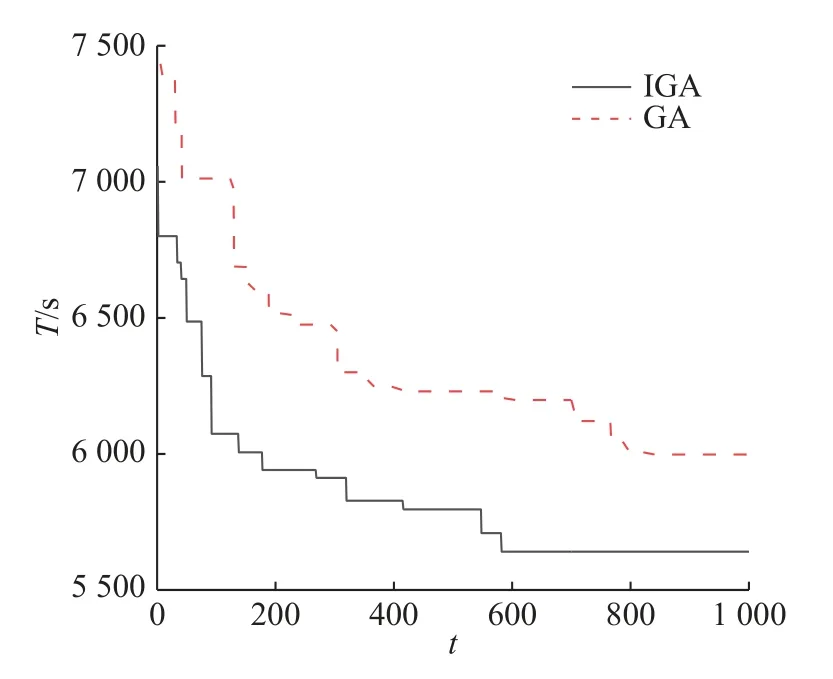
图9 订单规模为500 时算法迭代图Fig.9 Algorithm iteration diagram under order size of 500

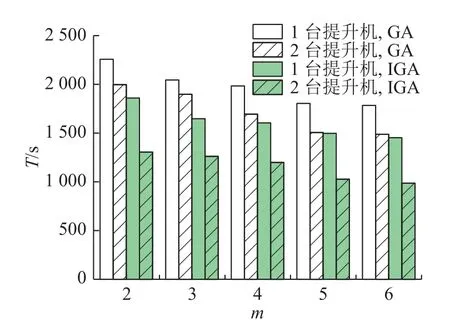
图10 订单规模为200 时算法优化的系统作业时间Fig.10 System operation time optimized by algorithm under order size of 200

4.3 系统结构分析

为了进一步对系统结构分析，比较单台和2 台提升机的情况对系统的影响.根据图9 中IGA 优化后的结果可知：1）随着四向车台数的增多，任务完成时间减少地越慢；2）采用2 台提升机的平均作业效率比采用1 台时高0.33%.为了验证订单规模对单双台提升机作业效率的影响，在单台提升机完成订单数为20 时选择3 台四向车可获得最低成本，因此在对单双台提升机分析时，选择6 台四向车完成订单数为50、100、200和500 的任务，其结果如图11 所示，选择2 台提升机相比于1 台提升机的效率分别提高了24.4%、38.7%、33.7%和43.2%，基本上随着订单的增加，2 台提升机相对于1 台提升机的效率优势也越来越明显.当系统中存在2 台提升机时，效率应比只有1 台提升机时快一倍.然而，由于四向车和提升机之间的相互作业会导致作业时间增加，随着订单数的增加，分配给2 台提升机的订单处于同一层并进行分类的概率增加.研究结果表明，在订单数为500 时效率达到43.2%，接近一倍.因此，在四向车台数大于提升机台数的情况下，订单数越大，采用2 台提升机的效率优势越大.

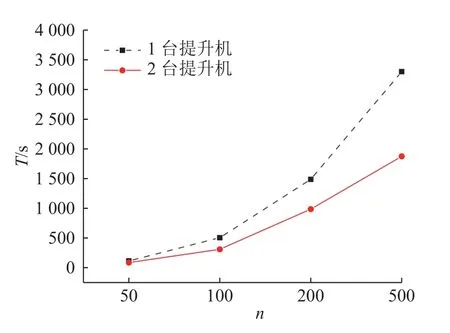
图11 不同订单规模不同提升机台数下完成任务时间Fig.11 Completion time under kinds of elevators and order sizes

5 结语

（1）建立以系统总任务作业时间为目标的数学模型.将系统的复合作业划分为入库作业、空载作业和出库作业，构建提升机和四向车在这3 种作业方式下完成任务所需时间的模型.

（2）设计改进的遗传算法.在系统提升机和四向车作业特点下，将出入库任务进行分类并对遗传算法进行改进.

（3）实例仿真结果表明，改进后的算法能有效解决所研究问题，四向车和提升机的台数对系统作业时间存在影响，为了提高系统作业效率，可根据订单规模安排设备台数.

本研究未考虑设备的加减速和四向车在同层作业的冲突问题，为了符合仓库实际运行情况，进一步研究可以在水平方向建模时考虑四向车的冲突问题，在设备上考虑加减速问题，在系统结构上可考虑依据存储货物类型增减每组货架的排数.