中央传动齿轮箱复杂油路性能仿真

吴超琦，罗健，周莹，娄鹏，尉玉

(中国航发商用航空发动机有限责任公司，上海 200241)

航空发动机是由众多相关的子系统组成的[1].传动系统作为重要子系统之一，其主要功能是为发动机提供动力[2].齿轮箱作为传动系统重要部件，在发动机高速运行时，各个齿轮之间相对摩擦会产生大量热量，润滑不足会导致传动系统温度过高[3]，因此在传动系统齿轮箱结构设计之前，对其进行仿真分析非常重要.

大量学者对于传动系统齿轮箱的润滑油仿真分析进行了研究.梁作斌等[4]研究航空发动机中央传动锥齿轮的润滑油流动，发现该齿轮的风阻损失占据总损失的70%.王翱等[5]基于Flowmaster一维仿真软件对齿轮箱的润滑系统性能进行稳态和瞬态仿真，验证润滑系统能够满足齿轮箱的润滑需求.葛玉柱等[6]利用Flowmaster 软件综合温度、润滑油黏度参数分析齿轮箱的润滑系统特性.王秋菊等[7]采用复合直接迭代法对高速齿轮润滑状态进行分析，得到不同功率和转速对于齿轮表面油膜温度和厚度的影响关系.Franco 等[8]采用滑移网格和多相流模型对齿轮箱内的流动进行建模，结果表明齿轮直径和厚度对齿轮箱内的搅油影响较大.Dai 等[9]利用CFD 分析齿轮速度对于风阻损失的影响，计算表明齿轮转速越高，风阻功率损失越大.Zhu 等[10]通过CFD 计算发现风阻功率损失随着齿轮速度的增加而急剧增加，相比没有挡板的锥齿轮，封闭式锥齿轮的风阻功率损失迅速下降80%.

综上，对齿轮箱润滑油的仿真分析研究主要集中在齿轮箱内搅油损失和对齿轮箱润滑系统的一维系统仿真，对齿轮箱内油路的润滑油流动的三维仿真分析较少.在传动齿轮箱结构设计过程中，油路结构是否合理与整个传动齿轮箱的性能是否满足设计要求有直接关系.采用三维仿真对齿轮箱内部油路结构分析计算，通过计算结果校核内部油路结构各处滑油体积流量分配和喷孔外部流线圆柱度（即外部流线的发散程度），能为性能评估提供有力的参考和依据.基于此，本研究以某航空发动机传动系统中央传动齿轮箱[11]复杂油路结构为研究对象，通过三维流体分析，预测发动机不同供油压力下，油路体积流量及油路喷嘴喷孔外部流线的流向关键参数，并进一步建立该油路结构的供油压力-体积流量数学模型.

1 计算模型

1.1 几何模型和计算网格

如图1 所示为中央传动齿轮箱的供油模型图.供油模型总共有2 个供油路，滑油从总供油口流入，通过三通阀后，流入收油环供油路和机匣供油路.整个油路模型共设有6 个滑油喷嘴，为收油环、齿轮啮合区、轴承和传动杆花键提供润滑冷却.

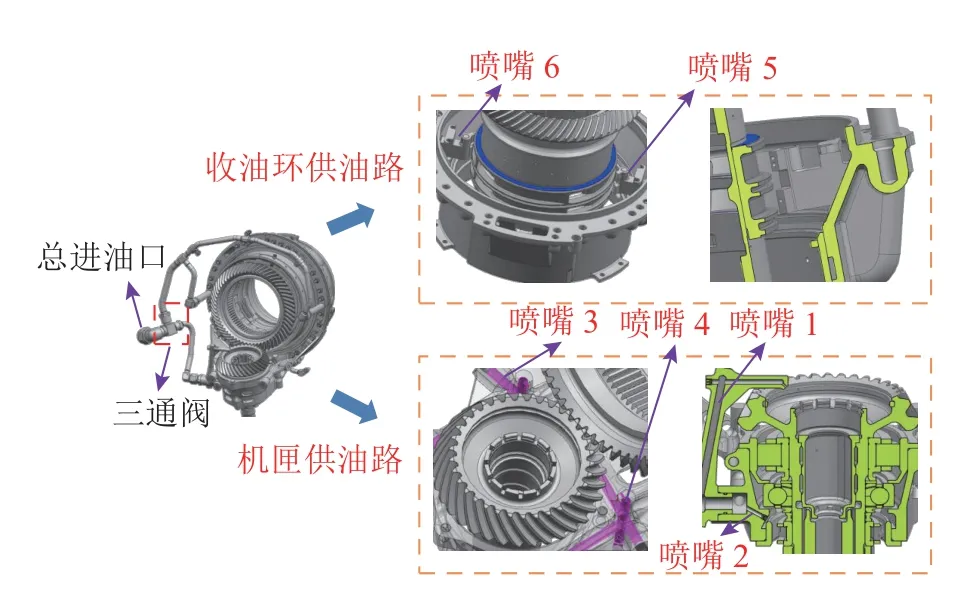
图1 中央传动齿轮箱的供油模型Fig.1 Oil supply model of inlet gearbox

如图2 所示为中央传动齿轮箱供油油路“双通道”和“单通道”模型的计算流体域和体网格模型.“双通道多喷嘴”油路模型包含收油环供油路和机匣供油路，在收油环供油路上滑油流经管路段1～3，从喷嘴5、6 喷出为收油环供油；在机匣供油路上滑油流经管流段4 后，部分滑油从喷嘴1流出为传动杆花键供油，剩余滑油从喷嘴2～4 流出，为齿轮啮合区和轴承供油，这3 个喷嘴均集成于齿轮箱单元体机匣上，统称为机匣喷嘴.具体的管路段和喷嘴信息如表1、2 所示.表中，dp、Lp分别为管流段直径、长度，dn、Ln分别为喷孔直径、长度.“单通道多喷嘴”油路模型，是以管流段1、4 的入口面作为滑油的进口，分别对收油环供油路和机匣供油路进行建模分析计算.

表1 “双通道多喷嘴”油路模型管流段信息Tab.1 pipe information of two channel multi-nozzle oil circuit model

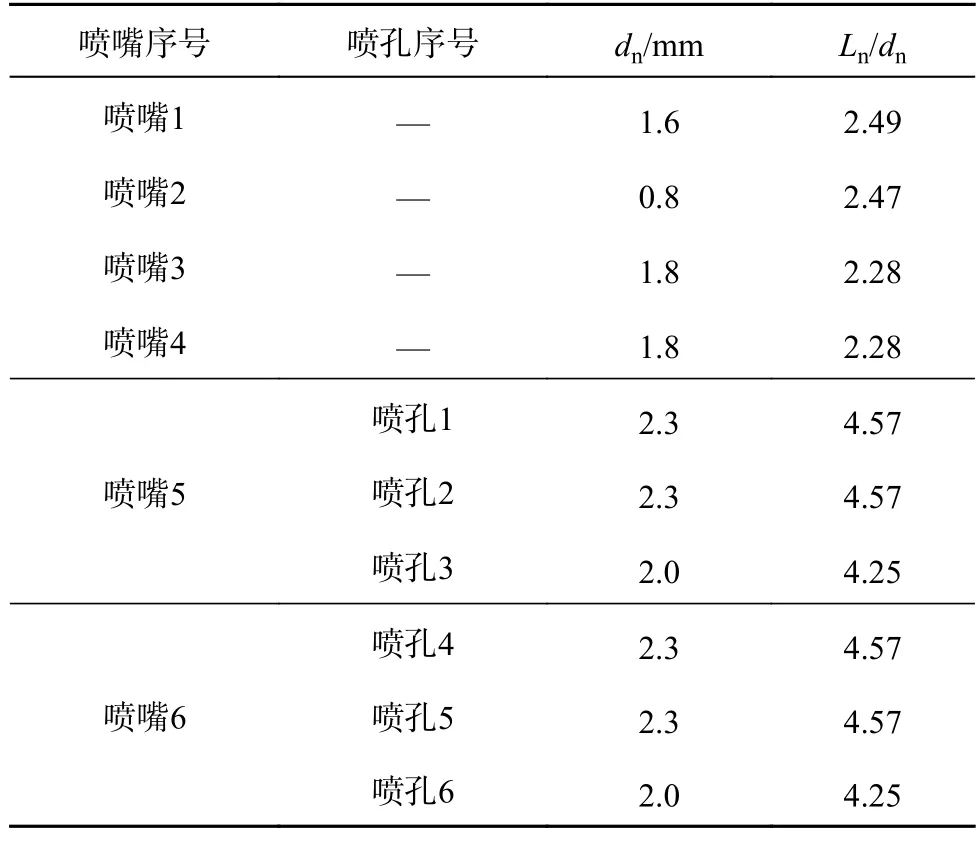
表2 “双通道多喷嘴”油路模型滑油喷嘴信息Tab.2 Nozzle information of two channel multi-nozzle oil circuit model

图2 油路模型流体域与体网格Fig.2 Fluid domain and volume grid of oil circuit model

中央传动齿轮箱油路结构较复杂，采用全六面体网格对油路计算域模型进行网格划分，对每个喷嘴局部区域网格加密，喷嘴最小网格为0.015 mm，最大网格为0.25 mm，各个管流段做到网格自然过渡，最大网格不超过0.6 mm，油路模型流体域和体网格如图2 所示.

1.2 物性参数和边界条件

滑油物性参数选取80 ℃对应的物性参数[12]，密度为948.7 kg/m3，动力黏度为0.007 8 kg/(m·s)，该温度和中央传动齿轮箱体积流量试验温度条件一致.

计算域入口采用压力入口（pressure inlet）边界类型，给定表压，本次计算的供油压力（表压）分别为0.05、0.10、0.15、0.20、0.25、0.30 MPa，计算域出口采用压力出口（pressure outlet）边界类型，给定背压0 MPa（表压）.

1.3 求解设置

采用压力基求解器进行稳态求解，用Realizablek-ε 湍流模型[13-15]封闭方程组，壁面函数采用增强型壁面函数[16-17]（enhanced wall treatment），尽可能确保流体域近壁面第1 层网格质心到壁面的无量纲距离Y+不大于2，压力-速度耦合采用SIMPLE算法[18-19].

为了验证网格无关性，以中央传动齿轮箱“双通道多喷嘴”油路模型为研究对象，划分不同疏密性的体网格模型，体网格的总数分别是527、793、905 万.油路的入口和出口采用相同的边界条件，以油路模型的体积流量作为网格无关性检验指标.计算结果表明，在0.25 MPa 的供油压力下，3 个不同的体网格方案对应的体积流量计算结果分别为27.31、29.84、29.86 L/min，结合计算资源和时间成本考虑，最终选取体网格总数为793 万的方案进行仿真和结果分析.

2 计算结果分析

2.1 计算结果验证

在80 ℃供油温度下，对比不同供油压力下“双通道多喷嘴”油路模型的体积流量计算结果以及最大试验供油压力（0.25 MPa）下各个滑油喷嘴的喷孔外部流线发散程度和中央传动齿轮箱体积流量-流向的试验结果.

如表3 所示为供油压力p=0.05～0.25 MPa 时，“双通道多喷嘴”油路模型体积流量qV计算结果和试验结果的对比.表中，e为误差.可以看出，不同供油压力下，体积流量计算结果和试验结果较相近，最大误差不大于4%，两者较吻合.

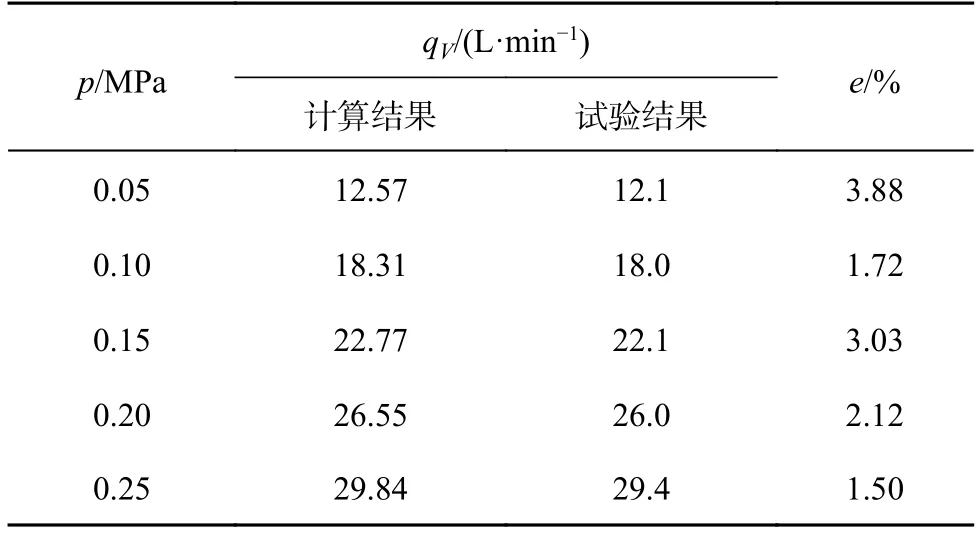
表3 不同供油压力下体积流量计算和试验结果的对比Tab.3 Comparison of calculation and test results of oil volume flow rate under different oil supply pressures

在0.25 MPa 供油压力下，齿轮啮合区和传动杆花键供油喷嘴的外部流线计算结果和试验的对比如图3 所示.可以看出，仿真计算得到的2 个供油喷嘴的外部流线发散程度和喷射位置均与试验结果较吻合.

以上结果充分表明Realizablek-ε 湍流模型能够有效预测不同供油压力下中央传动齿轮箱复杂油路模型体积流量并有效捕捉其三维流动特性.

2.2 “双通道多喷嘴”油路模型的计算结果

2.2.1 流线计算结果 如图4 所示为供油压力为0.25 MPa 的工况下，“双通道多喷嘴”油路模型的内部流线图.图中，v为速度.可以看出，在油路的管路段中，沿程的阻力较小，流线平直，趋于“平推流”的流动形式[20]，管流段内的流速均没有超过5 m/s；当流体流经喷孔段区域时，油路中的流通面积突然减小，导致流体流动的速度突然变大，喷嘴喷孔区域的最大流线速度均超过20 m/s，流线的最大速度均出现在每个滑油喷嘴的喷孔区域中.

图4 “双通道多喷嘴”油路模型的内部流线Fig.4 Internal streamline of two channel multi-nozzle model

从每个喷嘴局部放大的流线图中不难看出，在进入喷孔区域之前，喷嘴内部流线较平直；在流体流入喷孔前，受到近壁面和喷孔段流通面积减小的影响，喷孔局部区域内形成强烈的涡旋，流动情况较复杂；在流体进入喷孔段后，速度突然增加，局部阻力损失较大，由于受到局部区域形成的涡旋影响，喷孔内的流线亦呈旋流流动的形式，流体无法以“平推流”的方式从滑油喷嘴的喷孔流出.

中央传动齿轮箱油路模型中有多个喷嘴为收油环、齿轮啮合区、轴承和传动杆花键等多个区域提供润滑和冷却.如图5 所示为油路模型每个喷嘴的喷孔外部流线.可以看出，每个滑油喷嘴的喷孔外部流线的发散程度均较小，没有出现外部流线严重发散的情况.

图5 “双通道多喷嘴”油路模型的喷孔外部流线Fig.5 External streamline of two channel multi-nozzle model

如图6 所示为油路模型中每个喷嘴的喷孔外部流线喷射的位置示意，将中央传动齿轮箱中的齿轮、收油环、机匣和轴承结构简化，划分网格，将其和计算得到的外部流线进行比对.可以看出，流线能够完全喷入收油环收油口，为齿轮轴承供油润滑的喷嘴外部流线发散程度较小，流线喷射的位置能满足为齿轮轴承供油的要求.

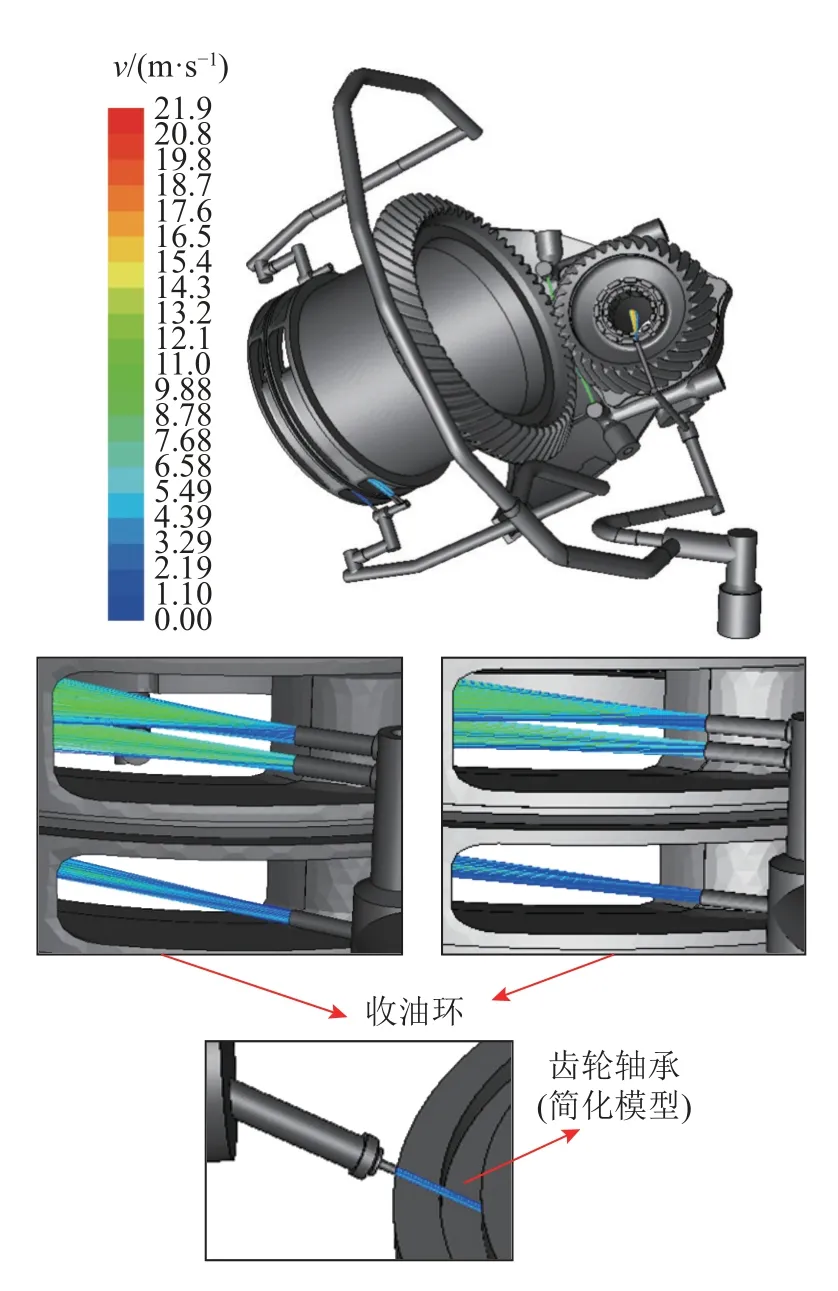
图6 油路模型喷孔外部流线喷射位置Fig.6 External streamline injection position of nozzle orifices in oil circuit model

2.2.2 压力计算结果 如图7 所示为0.25 MPa 供油压力下，整个油路模型的压力分布图.可以看出，在油路模型各个管流段区域，压力变化相对较小，这是由于管流段内的流速相对较低，流体沿程阻力较小，压力损失较小[21].当流体流经喷孔段区域时，油路中的流通面积突然减小，导致流体流动的速度突然变大、局部区域的流动阻力增加，油路模型中喷嘴喷孔段的压力变化最大.如表4所示为油路压力损失比例计算结果.表中，Δp为压力损失，pro 为压力损失占比.可以看到，各个喷嘴压力损失占比均大于20%，而管流段压力损失占比不足3%，油路中喷嘴所占的压力损失比例最大.

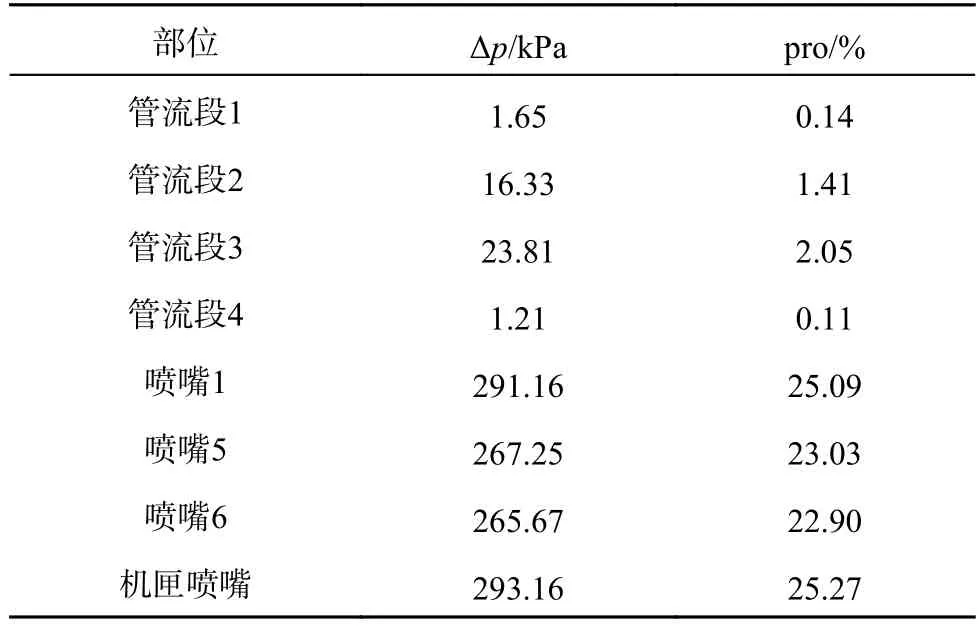
表4 “双通道多喷嘴”油路模型的压力损失比例Tab.4 Pressure loss proportion of two channel multi-nozzle model

图7 “双通道多喷嘴”油路模型的压力分布Fig.7 Pressure distribution of two channel multi-nozzle model

2.2.3 体积流量计算结果 体积流量系数Cd为反映齿轮箱单元体上供油喷嘴流阻的关键参数.如图8 所示分别为机匣供油路和收油环供油路上的滑油喷嘴，在不同供油压力p下的体积流量系数Cd计算结果.可以看出，整个齿轮箱油路模型上的滑油喷嘴，其对应的体积流量系数为0.64～0.75，随着油路入口供油压力增加，油路内滑油雷诺数增加，所有滑油喷嘴体积流量系数也增加，滑油喷嘴体积流量系数和油路内滑油雷诺数呈正相关的关系.对于相对位置和结构参数（直径和长径比）均相同的喷嘴（如喷嘴3、4），不同供油压力下对应的体积流量系数结果相近，体积流量系数曲线的变化趋势几乎相同.

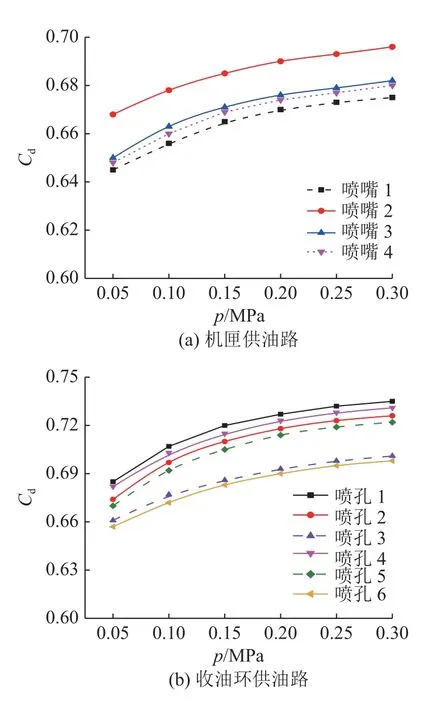
图8 不同供油压力下的体积流量系数Fig.8 Oil volume flow coefficient at different oil supply pressures

2.2.4 体积流量计算结果 基于表3 的体积流量结果，得到体积流量qV随着供油压力p变化的拟合曲线.可以看出，仿真结果计算得到的体积流量随供油压力的变化趋势和试验结果的一致，体积流量随供油压力的不同，呈二次函数的变化形式.基于试验数据得到的供油压力-体积流量数学模型方程如下：

由于中央齿轮箱体积流量-流向试验台的滑油泵功率不足，中央传动齿轮箱的最大试验供油压力仅为0.25 MPa，而高温起飞工况对应的压力为0.30 MPa，该工况是考察中央传动齿轮箱性能是否满足设计要求的重要工况，基于所建立的供油压力-体积流量数学模型，进一步推算该工况下油路结构所对应的体积流量.

如图9 所示为体积流量随着供油压力变化得到的“外延曲线”.基于所建立的供油压力-体积流量数学模型，对体积流量随供油压力变化的拟合曲线采用“外延法”，得到0.30 MPa 供油压力下体积流量，将之与仿真计算结果和设计要求对比.可以看出，在0.30 MPa 供油压力下，体积流量的“外延值”为31.70 L/min，和仿真计算得到的32.53 L/min相近，两者均在设计要求对应的（35.05±3.5）L/min范围内.表明对中央传动齿轮箱不同供油压力下的体积流量试验数据进行适当外延，能够有效预测更高供油压力下中央传动齿轮箱油路的体积流量，外延法可以作为评估中央传动齿轮箱油路结构性能的有利方式.

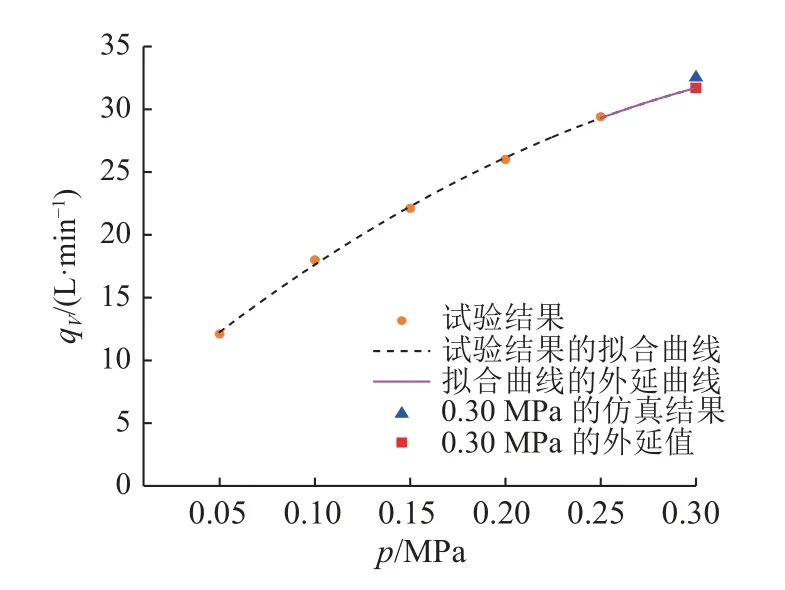
图9 体积流量随供油压力变化的外延曲线Fig.9 Extension curve of oil volume flow rate with oil supply pressure

2.3 “单通道多喷嘴”油路模型的计算结果

2.3.1 流线计算结果 如图10 所示为“单通道多喷嘴”油路模型在0.25 MPa 供油压力下的压力分布和内部流线图.可以看出，收油环供油路和机匣供油路的供油喷嘴喷孔段区域内部流动较复杂，产生了旋流，局部速度较大，同时喷孔段的流通面积减少，导致该区域的压力损失较大.

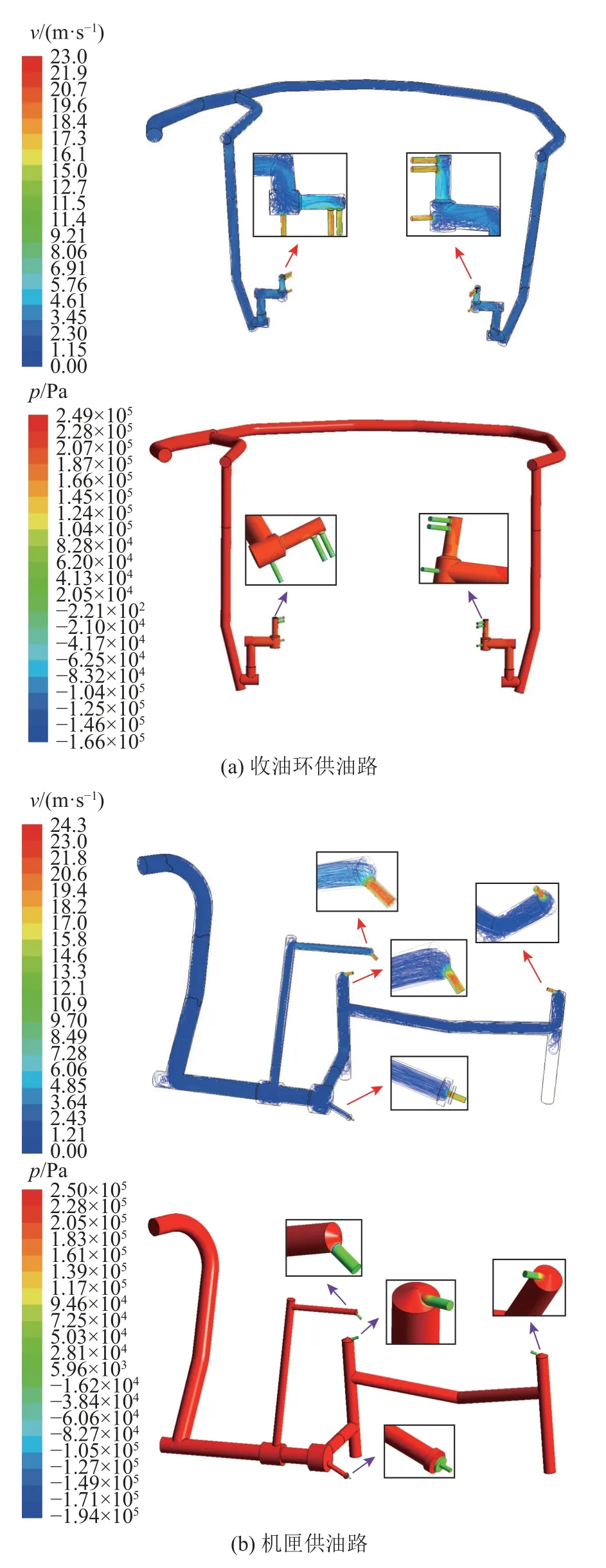
图10 “单通道多喷嘴”油路模型压力分布和内部流线Fig.10 Pressure distribution and internal streamline of one channel multi-nozzle model

2.3.2 体积流量计算结果 基于供油压力0.05～0.30 MPa 对应收油环供油路和机匣供油路的体积流量计算值，绘制曲线并对之进行拟合，如图11所示，可以得到“单通道多喷嘴”油路模型的供油压力-体积流量数学模型.

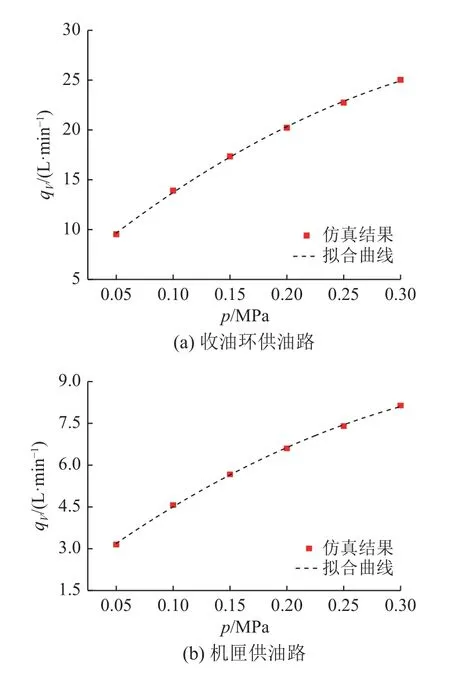
图11 体积流量随供油压力变化的拟合曲线Fig.11 Fitting curve of oil volume flow rate with oil supply pressure

收油环供油路的压力-体积流量拟合曲线方程如下：

机匣供油路的压力-体积流量拟合曲线方程如下：

由图11 可知，“单通道多喷嘴”油路模型供油压力和体积流量两者之间呈二次函数关系，在0.05～0.30 MPa 内，收油环供油路对应的体积流量最小值、最大值分别为9.53、25.03 L/min，机匣供油路对应的体积流量最小值、最大值分别为3.15、8.14 L/min.基于三维流体仿真所得到的中央传动齿轮箱“单通道多喷嘴”复杂油路结构压力-体积流量的数学模型，能够更全面地评估中央传动齿轮箱复杂油路结构的性能.

3 结论

(1) 基于Realizablek-ε 湍流模型所建立的复杂油路结构三维仿真模型能够有效捕捉 “双通道多喷嘴”复杂油路结构的三维流动特性；体积流量计算结果和滑油喷嘴喷孔的外部流线喷射位置和与试验结果均较吻合，能为中央传动齿轮箱的性能评估提供依据，验证装置的复杂油路结构能够满足设计的要求.

(2) 对供油压力0.05～0.25 MPa 的体积流量曲线进行适当外延得到高温起飞工况下（供油压力为0.30 MPa）“双通道多喷嘴”复杂油路结构的体积流量，计算值、仿真结果和设计要求均较吻合，“外延法”能够运用于复杂油路结构的性能评估.

(3) 中央传动齿轮箱复杂油路结构喷嘴的喷孔段局部区域由于流通面积突然减小，内部会产生旋流，局部速度大，压力损失较大，油路管流段内滑油的流动接近于“平推流”，流动速度相对较低，沿程阻力损失较小，压力变化较小.

(4) 在不同供油压力下，油路结构的滑油喷嘴体积流量系数会有所不同，随着供油压力增加，所有滑油喷嘴的体积流量系数呈缓慢增加的趋势，两者之间呈正相关的关系；对于相对位置、喷孔直径、长径比均相同的喷孔，对应的体积流量系数变化曲线几乎相同，不同供油压力下对应的体积流量系数计算结果相近.

(5) 利用复杂油路结构的三维仿真模型进一步对“单通道多喷嘴”复杂油路结构的性能进行分析，结果表明，当供油压力为0.05～0.30 MPa 时，收油环供油路和机匣供油路的供油压力和体积流量呈现二次函数的变化关系，所得到的供油压力-体积流量数学模型能够更全面地支撑中央传动齿轮箱复杂油路结构在不同工况点下的性能评估和结构设计.

(6) 本研究采用三维流动仿真的方式对中央传动齿轮箱内的复杂油路建立了压力-体积流量数学模型，但是并未针对附件齿轮箱和转接齿轮箱这2 个齿轮箱内的复杂油路建立压力-体积流量数学模型，下一步会将这种方式应用于这2 个齿轮箱的复杂油路模型，对其建立压力-体积流量数学模型.