基于个体预测的动态多目标优化算法

王万良，陈忠馗，吴菲，王铮，俞梦娇

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

在实际生活中，存在许多具有多个目标的优化问题，并且这些目标之间是互相冲突的，此类问题被称为多目标优化问题(multi-objective optimization problems,MOPs)[1].实际生活中环境是不断发生变化的，如果MOPs 的目标函数、约束和参数会随着环境变化而改变，MOPs 则转化为动态多目标优化问题(dynamic multi-objective optimization problems,DMOPs).在处理复杂的DMOPs 时，传统的多目标优化算法(multi-objective optimization algorithms,MOAs)[2-7]明显具有局限性.随着环境的变化，Pareto 最优解集 (Pareto-optimal set，PS)[8]和Pareto 前沿 (Pareto-optimal front，PF)不断发生变化，传统的MOAs 会在环境变化中逐渐丧失种群的多样性，种群在某一时刻陷入局部收敛而不再随环境发生变化.因此，需要动态多目标优化算法(dynamic multi-object optimization algorithms,DMOAs)[9-14]及时地响应环境变化，从而追踪到变化后的PS 和PF.

近年来，DMOAs 不断被提出，并应用于各个领域，例如：调度[15]、机械设计[16]、资源管理[17]、路径规划[18]等.为了解决DMOPs,研究大致可以划分为3 大模块：环境变化检测[19-20]、环境变化应答机制[9-14,21-22]、静态多目标优化算法[2-7].其中静态多目标优化算法大多是为了提高收敛速度，例如：NSGA-II[5]、RM-MEDA[6]、MOEA/D[7]等.环境变化检测用于检测环境的变化，为后面设计应答机制提供指导，而变化应答机制是解决DMOPs 的重要研究目标.变化应答机制大多利用多样性引入机制[21]、预测机制[9-14]、记忆机制[22]等方式来响应环境的变化.其中预测机制对周期性问题和非周期性问题均有不错的效果，该机制通过利用历史信息或者其他方法来预测环境变化后的最优解，如果预测足够准确，那么预测机制对DMOPs 非常有效.Zhou 等[10]提出种群预测策略(population prediction strategy,PPS),该策略应对DMOPs 较有效，但由于在早期阶段缺乏历史信息的积累，前期效果较差.Zou 等[11]提出基于中心点和Knee 点的预测策略(prediction strategy based on center points and knee points,CKPS),该策略将Knee 点引入预测种群，可以更加准确地追踪PF,但后期效果不够理想.Li 等[12]提出基于特殊点的预测策略(predictive strategy based on special points,SPPS)，利用Knee点、近边缘点、近中心点等特殊点快速地跟踪PF，该策略进一步提高了种群的多样性，但种群中心点的预测缺乏反馈校正，预测的准确性还有待进一步提高.Rong 等[13]提出多向预测策略(multidirectional strategy,MDP),该策略利用先前环境中多个代表性解所确定的多个方向来预测PS 在决策空间中的位置，从而提高了解决DMOPs 的性能.Chen 等[14]提出结合混合预测和突变策略的变化响应机制(change response mechanism by combining mixed prediction strategy and mutation strategy,HPPCM)，混合预测策略协调基于中心点的预测和基于引导个体的预测，而突变策略可以处理不可预测的环境变化，从而快速适应各种环境变化.

针对上述不足，本研究提出基于个体预测的动态多目标优化算法，其主要贡献如下.1) 提出参考点联系算法，引入该算法筛选的特殊点，并通过新的特殊点预测策略快速地响应环境变化.2) 提出针对种群中心点预测的反馈校正机制，对种群中心点预测非支配解集的预测步长进行反馈校正，使预测更加准确.3) 提出混合多样性维持机制，引入拉丁超立方抽样和精度可控的突变策略分别生成的随机个体，以提高种群的多样性，避免种群陷入局部收敛.

1 相关工作

1.1 动态多目标优化相关概念

DMOPs 定义[23]如下：

式中：F(x,t) 为m维的目标向量，x=[x1,x2,···,xn]T为n维的决策变量，定义域为Ω,g(x,t) 和h(x,t) 分别为不等式约束以及等式约束，t表示时间变量.

式中：τ 为迭代数，nt为环境变化程度，τt为变化频率.

定义1.如果x1和x2在时间t满足以下条件：

则x1可以支配x2，记作x1≺x2.

定义2.在t时刻，如果不存在个体x′∈Ω 支配个体x，则x为问题(1)(式（1）) 在t时刻的一个Pareto 最优解，P St为问题(1)在t时刻所有Pareto最优解的集合.定义如下：

定义3.在t时刻，PSt在目标空间的映射被称为 PFt：

根据PF 和PS 动态变化的不同组合，确定4 种不同类型的DMOPs，如表1 所示.

表1 4 种不同类型的DMOPsTab.1 Four different types of DMOPs

1.2 RM-MEDA

RM-MEDA[6]是改进后的分布估计算法，可以在一定的光滑性假设下，即在Karush-Kuhn-Tucker假设下，导出连续MOP 的PS,在决策空间中能够形成分段连续的m-1 维流形.RM-MEDA 不是直接使用种群中的局部信息生成新的种群，而是充分利用当前种群提供的全局信息，因此RM-MEDA具有更强的启发式优化能力.RM-MEDA 的流程图如图1 所示.

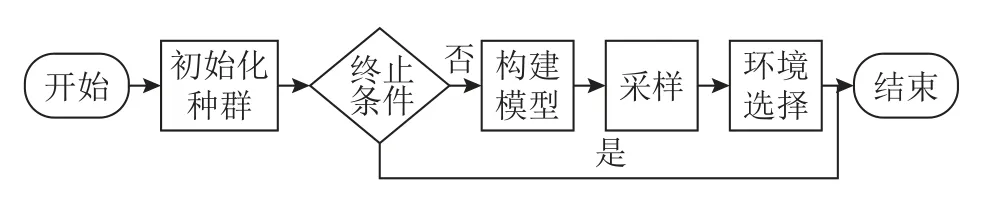
图1 RM-MEDA 流程图Fig.1 Flow chart of RM-MEDA

1.3 参考点

参考点常常被用来解决多目标优化问题上的收敛性和多样性问题，在Das 等[24]所提方法的基础上，Deb 等[25-26]提出基于参考点的多目标优化算法(NSGA-III),利用预定义的参考点对选择个体的方法进行改进，以维持种群之间的多样性，后续将NSGA-III 扩展到求解一般约束多目标优化问题.本研究的参考点采用Das 等[24]的方法设计，所设计的参考点在超平面上均匀分布.假设M个参考点的集合为R={r1,···,ri,···,rM}，生成参考点ri：

式中：i=1,2,···,M,j=1,2,···,m,M为参考点的数量，H为每个目标上划分的数目，m为目标函数的个数.

在Das 等[24]的方法中，参考点数量M的表达式为

通常，参考点的数量与种群的大小一致，本研究根据种群中非支配解集的大小设置参考点的数量.

2 基于个体预测的动态多目标算法

2.1 特殊点集

追踪PS 和PF 一直是解决动态多目标优化问题的热点，本研究提出参考点联系算法，利用该算法筛选的特殊点来追踪PF，从而实现更快的收敛.

参考点联系算法是将预定义的参考点与非支配个体关联起来.参考点与原点连接作为该参考点的参考向量，计算每个参考向量与非支配个体的距离，参考点与离其参考向量最近的非支配个体关联.由于参考点是均匀分布在超平面上的，若有非支配个体关联较少的参考点或没有关联参考点，说明附近有其他非支配个体与其竞争，则这些个体不具备较好的多样性；反之，关联较多参考点的非支配个体具有较好的多样性.如图2所示，非支配个体A关联了3 个参考点，其多样性优于关联2 个参考点的B、C、D以及关联1 个参考点的E，而F、G作为边界点则直接加入到特殊点集中.

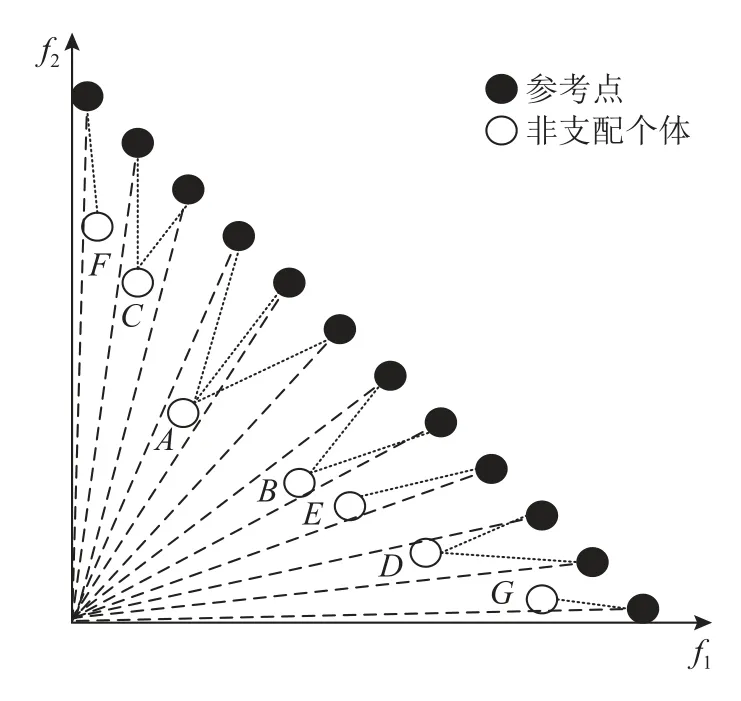
图2 非支配个体与参考点关联示意图Fig.2 Schematic diagram of association between non-dominant individuals and reference points

根据非支配个体关联参考点的数量，从多到少依次选择 num1个非支配个体加入特殊点集中.为了给筛选提供便利，预定义参考点的数量大于非支配解集的总数.参考点联系算法的具体步骤见算法1.

算法1 参考点联系算法

1）将种群分层，选择第1 层的个体为非支配个体.

2）根据非支配解集的大小，采用式(6)的方法设计参考点集R.

3）计算每个参考向量与非支配个体的距离，参考点与离其参考向量最近的非支配个体关联.

4）根据非支配个体关联参考点的数量，从多到少依次排列，按照顺序选择 n um1个非支配个体加入特殊点集.

除了以上筛选的点和边界点以外，本研究还采用文献[11]中的方法，选择Knee 点加入特殊点集，Knee 点是指在PF 上具有最大边际效用的点，在Knee 点附近，一个目标上有一个较小的改进，将会伴随着至少一个目标的严重退化.参考点联系算法在筛选过程中会避免出现和Knee 点重合的情况，且当实际筛选点的数量少于 n um1时，从非支配解集中随机选择个体补齐.

选择参考点联系算法筛选的点、边界点和Knee 点作为特殊点代表整个PF,而对特殊点集的预测能快速地响应环境变化，加快种群的收敛.采用文献[27]、[28] 的方法，提出特殊点预测策略，在图3 中，通过例子来说明该特殊点预测策略的思想.首先计算t时刻特殊点集的最小值点mint和最大值点maxt:

图3 特殊点预测策略示意图Fig.3 Schematic diagram of special points prediction strategy

根据t时刻的mint和maxt以及可以预测出t+1 时刻的最小值点mint+1和最大值点maxt+1，mint+1和maxt+1则组成了t+1 时刻的决策空间：

利用特殊点预测出t+1 时刻最小值点和最大值点组成的决策空间，然后进一步预测t+1 时刻的特殊点集.它不是一个准确的预测，因此增加了一个高斯扰动，若为t时刻的一个特殊点，则预测的公式为

算法2 特殊点预测策略

输入：特殊点集 specialt,特殊点集的大小Ns.

输出：预测的t+1特殊点集 pops.

1）根据式(8)计算t时刻和t-1 时刻特殊点集的最小值点mint和mint-1以及最大值点maxt和maxt-1.

2）根据式(9)计算t时刻最小值点和最大值点第i维的运动方向

3）根据式(10)预测t+1时刻的最小值点mint+1和最大值点maxt+1.

4）根据式(11)预测t+1 时刻的特殊点集.

2.2 种群中心点预测的反馈校正机制

种群中心点的预测方法[9-11]被广泛应用到种群的预测中，该预测方法通常被用来预测非支配个体，但由于缺乏误差反馈和校正机制，预测的准确性还有待进一步提高，因此，本研究采用了针对该预测方法的反馈校正机制[29]来弥补这一缺陷.

首先须构建一个代表个体，将t时刻非支配解集的中心点Ct作为代表个体：

式中：PSt为t时刻种群的非支配解集，xt为非支配个体.

然后对代表个体进行预测：

式中：Ct+1为预测的t+1 时刻非支配解集的中心点；Pt=Ct-Ct-1表示初始预测的步长和方向，Ct-1为t-1 时刻非支配解集的中心点.

如图4 所示，基于Ct+1，在预测步长的范围内，沿初始预测的正负方向对最优变量均匀采样，生成 2N个搜索个体S={s1,···,si,···,s2N}：

图4 决策空间变量的步长探索Fig.4 Step size exploration of decision space variables

最后对这组搜索个体S={s1,···,si,···,s2N} 和Ct+1进行评估，将非支配个体存储到外部存档A中，A={a1,···,ai,···,a|A|},在A中随机选择一个非支配个体ai.非支配个体ai优于Ct+1,其对应的预测步长也优于初始预测的步长，因此初始预测步长可以通过Ct+1和ai之间的向量差 Δ进行修正：

最优变量的选择，根据非支配解集中每个维度决策变量的标准差决定，选择标准差较小的变量作为最优变量.根据文献[29]、[30]中单一最优变量的定义，如果一个决策变量是单一最优的，那么所有解在该决策变量上的值是相同，因此本研究选择非支配解集中标准差较小的变量作为最优变量.反馈校正机制的具体步骤如算法3 所示.

算法3 反馈校正机制

输入：非支配解集PSt

输出：校正后的预测步长Pt

1）根据式(12)计算t-1时刻和t时刻非支配解集的中心点Ct-1和Ct,Ct作为代表个体.

2）根据式(13)对Ct进行预测，得到预测的t+1 时刻非支配解集的中心点Ct+1.

3）计算非支配解集中每个维度决策变量的标准差，选择标准差较小的变量为最优变量Vstd.

4）根据式(14)生成 2N个搜索个体S={s1,···,si,···,s2N}.

5）重新评估Ct+1和搜索个体S={s1,···,si,···,s2N}，并将非支配个体存储到A中.

6）对于j∈Vstd，利用式(15)对Pt进行校正.

根据校正后的预测步长对非支配个体进行预的非支配个体，分别对非支配个体进行小、中、大3 种步长的预测[31]:

测.为了使预测的非支配个体更接近t+1 时刻真实式中：xt+1表示t+1 时刻的非支配个体；rs 为沿移动方向的移动步长，使用3 种不同的值(0.5,1.0,1.5)表示，分别代表非支配个体小、中、大3 种步长的预测，其中，小步长和大步长的预测作用在同一非支配解集，各预测一半的非支配个体，3 种步长预测后的种群共同构成了t+1 时刻的非支配解集.

2.3 混合多样性维持机制

在动态环境中，保持多样性是非常重要的，本研究提出混合多样性维持机制，通过拉丁超立方抽样[32]在式(8)～(10)预测的t+1 时刻的决策空间和t时刻特殊点的最小值点和最大值点组成的决策空间中分别生成N1个随机个体.除此之外，在Zhang 等[33]提出的精度可控突变算子的基础上，提出精度可控的突变策略，对非支配解集进行突变，生成随机个体.所提出的精度可控突变算子表达式如下：

式中：Δβ=Δα+1/10Random(q)×Gaussian(0,std),其中Δα=1/10Random(q)×Random(9)，std 为非支配解集中每个维度决策变量的标准差；i=0,1,···,n；xi为x的第i维决策变量；为x′突变的第i维决策变量.

精度可控的突变策略的具体步骤如算法4 所示.

算法4 精度可控的突变策略

输入：非支配解集 PSt，x为PSt中的非支配个体

输出：随机解pop2

该策略对非支配解集突变生成随机个体，为了保证突变的随机个体仍具有较好的收敛性，只对非最优变量进行突变，变量r随机取1 或2，使突变可以生成均匀扩散的随机个体.Δβ 和 Δα 都用于控制变量的精度，Δβ 在 Δα 基础上增加了精度可控的高斯分布，在扩大了搜索范围的同时也可以通过比 Δα 更小的步长在决策空间中局部搜索最优解，理论上，本研究提出的精度可控的突变策略所突变的随机个体，具有更好的多样性和更均匀的分布.

2.4 IPS 算法详细描述

IPS 是在动态多目标进化算法的框架下进行的.IPS 在环境变化后产生新的初始种群，使新的种群能够对环境变化快速响应并追踪其变化的PF.算法5 是对IPS 的详细描述，IPS 的流程图如图5 所示.

图5 IPS 流程图Fig.5 Flow chart of IPS

算法5 IPS 算法

初始化：时间变量t:=0,初始化种群 pop,迭代次数计数器gt:=0,算法总进化代数gmax.

1）检测环境变化，如果环境没有发生变化，转步骤10）；否则，转步骤2）.

2）根据算法1 得到参考点联系算法筛选的点，和Knee 点、边界点一起作为特殊点.

3）利用式(8)～(10)预测t+1 时刻最小值点和最大值点组成的决策空间，并利用式(11)预测t+1 时刻的特殊点集 pops.

4）计算非支配解集的中心点Ct.

5）利用式(14)～(15)对式(13)的预测步长进行反馈校正，并利用校正的预测步长预测t+1 时刻的非支配解集 popNon-dom.

6）对式(8)～(10)计算的t时刻决策空间和预测的t+1时刻决策空间进行拉丁超立方抽样生成随机解 pop1.

7）根据算法4 对t时刻非支配解集突变生成随机解pop2.

8）得到新种群popt+1=pops+popNon-dom+pop1+pop2.

9）对popt+1执行RM-RMAD 中的环境选择算法.

10）用RM-RMAD 对种群进行优化.

11）如果gt＞gmax,则输出 popt并终止；否则gt:=gt+1，转步骤1）.

3 测试问题及评价指标

3.1 测试问题

采用几种常见的动态多目标测试问题，包括FDA 系列[23]和DMOP 系列[34]以及F5～F10 系列问题[6].其中，FDA 和DMOP 系列问题的决策变量之间是线性相关的，而F5～F10 系列问题的决策变量之间是非线性相关的.F9～F10 是更难收敛的测试问题，例如，F9 的Pareto 前沿在大部分时间内发生平稳变化，但偶尔会出现较大的环境变化，这会降低算法的收敛速度.在所有的测试问题中，FDA4 和F8 是三目标测试问题，其他是两目标测试问题.

3.2 性能指标

采用修正的反向代距离(modified inverted generational distance,MIGD)[11-12]和修正的超体积差(modified hypervolume difference,MHVD) 作为DMOAs 的性能评价指标，衡量算法在收敛性和多样性方面的性能.

反向代距离 (inverted generational distance,IGD)[35]被广泛应用到衡量算法的收敛性和多样性，IGD 指标的定义如下：

IGD 评价的是标准PF 和算法所得PF 的接近程度以及算法所得PF 中个体的分布性，MIGD 是IGD 的修改版本，它被定义为运行期间某些时间步长内的IGD 平均值：

式中：T为运行中的一组时间离散点集合.

MIGD 是综合的评价指标，可以评价算法在收敛性和分布性方面的性能，其值越小，说明算法的性能越好.

超体积差 (hypervolume difference,HVD)[36]测量的是标准PF 和算法所得PF 之间的超体积差，HVD 的评价指标如下：

式中：HV(S) 表示集合S的超体积.

MHVD 是对HVD 的修改版本，它被定义为运行期间某些时间步长内的HVD 平均值，其表达式如下：

4 实验结果与分析

4.1 参数设置

选择4 种策略与本研究所提的IPS 进行对比.4 种策略分别为种群预测策略(PPS)[10]、基于中心点和拐点的预测策略(CKPS)[11]、基于特殊点的预测策略(SPPS)[12]和结合混合预测和突变策略的变化响应机制(HPPCM)[14].5 种策略均采用RMMDEA[6]对问题优化.

对每个问题独立实验20 次，每次实验都会产生100 次环境变化，环境的变化程度nt=10,环境变化频率 τt=25,每次运行的总进化代数为2 500，种群大小设置为100，决策空间的维度n=20，在AR(p)模型中，参数p=3，历史信息序列长度设置为23.各个策略特定的参数设置如下.

1) CKPS 的Knee 点个数为9.

2) SPPS 在种群中心点预测非支配集的过程中将高斯扰动d=0.1.

3) HPPCM 中自主演化的代数 Δt=2.

4) IPS 中参考点联系算法筛选的特殊点个数num1=9，最优变量个数为2，搜索个体总数 2N=18，N1=25，q=2.

环境变化检测则通过选择种群中5%的个体来检测环境变化，目标值不匹配表明环境发生了改变.

4.2 性能评价的统计结果对比

在动态环境中，须讨论不同策略在不同时期的性能，因此，将100 次环境变化分为3 个阶段：第1 阶段包括前20 次环境变化；第2 阶段包括中间40 次环境变化；第3 阶段包括最后40 次环境变化.MIGD 和MHVD 的平均值和标准差如表2～5 所示.表中，粗体表示最佳值.采用Wilcoxon 秩和检验[37]在0.05 显著性水平上比较不同结果之间的显著性.

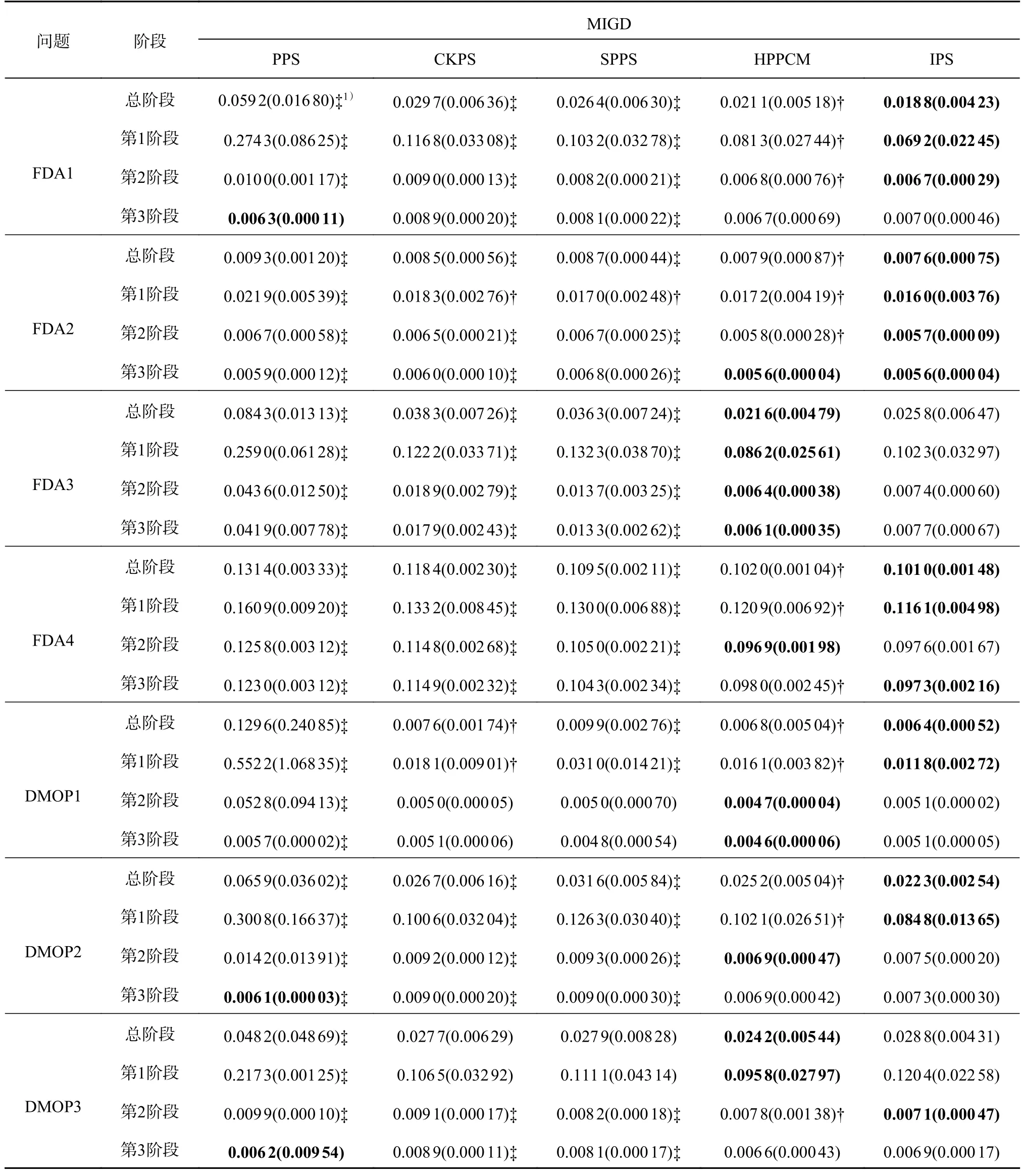
表2 5 种策略在FDA 和DMOP 上的MIGD 指标Tab.2 MIGD indicators for five strategies on FDA and DMOP

4.2.1 FDA 和DMOP 问题上的实验结果分析 如表2 所示为在FDA 和DMOP 系列问题上比较5 种策略的MIGD 指标，总阶段代表所有的环境变化.可以看出，1) 在总阶段和第1 阶段，IPS 有5 个MIGD 指标是最优的，HPPCM 有2 个MIGD指标是最优的.2) 在第2 阶段，IPS 有3 个MIGD 指标是最优的，HPPCM 有4 个MIGD 指标是最优的.3) 在第3 阶段，IPS 有2 个MIGD 指标是最优的，PPS 和HPPCM 有3 个MIGD 指标是最优的.

出现这样实验结果的原因如下.IPS 不需要经验的积累，其参考点联系算法筛选的特殊点可以加速种群的收敛，因此，在第1 阶段IPS 表现出了更好的性能.PPS 随着经验的积累，在后2 个阶段的某些测试问题上的MIGD 指标优于IPS 的.HPPCM 的混合预测机制注重收敛，可以快速地响应环境变化，因此在FDA 和DMOP 系列问题上也有较好的表现.对于3 个目标的测试问题，IPS 整体的性能要好于其他4 种策略，说明IPS 在高维动态多目标问题上有着更好的表现.

4.2.2 在F5～F10 问题上的实验结果分析 F5～F10是决策空间变量呈非线性相关的测试问题，如表3所示，在F5～F10 系列问题上比较了这5 种策略的MHVD 指标，MHVD 和MIGD 均为综合的评价指标，可以评价5 种策略在收敛性和分布性方面的性能.可以看出，IPS 和HPPCM 较其他3 种策略表现出了更好的性能.对于测试问题F5～F8,HPPCM 在第2、3 阶段的MHVD 指标大多优于IPS 的，原因如下：HPPCM 擅长追踪具有重大变化的PS 或PF,而IPS 的反馈校正机制和特殊点预测策略可以加速种群的收敛，因此IPS 在第1 阶段表现更好.对于复杂测试问题F9,IPS 的MHVD指标比其他4 种策略的都要好，这是因为IPS 在面对较大环境变化时仍能较快地收敛.CKPS 和SPPS 则在F10 测试问题上有着更好的表现，是因为其自适应的种群维持机制可以根据问题困难程度引入不同数量的个体.

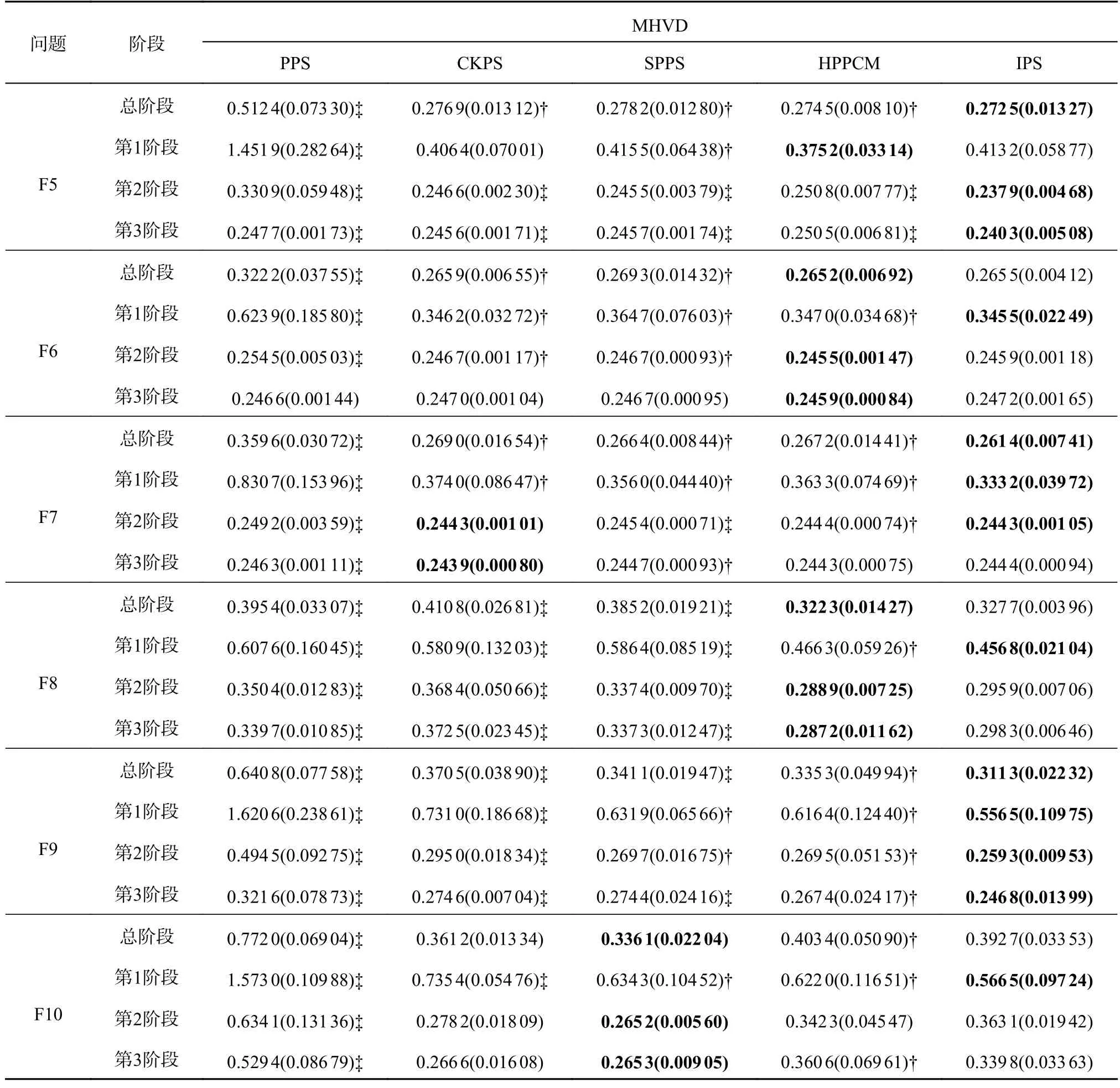
表3 5 种策略在F5～F10 上的MHVD 指标Tab.3 MHVD indicators for five strategies on F5 to F10

4.2.3 不同环境变化频率下的实验结果分析 为了检验5 种策略在不同环境变化频率下的性能，选择6 个具有代表性的测试问题，比较5 种策略对应3 种不同 τt的MIGD 和MHVD 指标，环境变化频率 τt分别设置为20、25 和30.如表4 所示，每种算法都有18 个MIGD 指标，其中IPS 有11 个MIGD 指标是最优的，HPPCM 有5 个MIGD 指标是最优的，SPPS 和CKPS 有1 个MIGD 指标是最优的，不难看出，5 种策略中IPS 和HPPCM 最优和次优的MIGD 指标是最多的，说明IPS 和HPPCM 比其他3 种策略的性能更好，另一方面，随着 τt的增加，5 种策略的性能均得到了提升，原因是较大的 τt有更多的迭代次数使种群在环境变化之前找到近似的 PS.

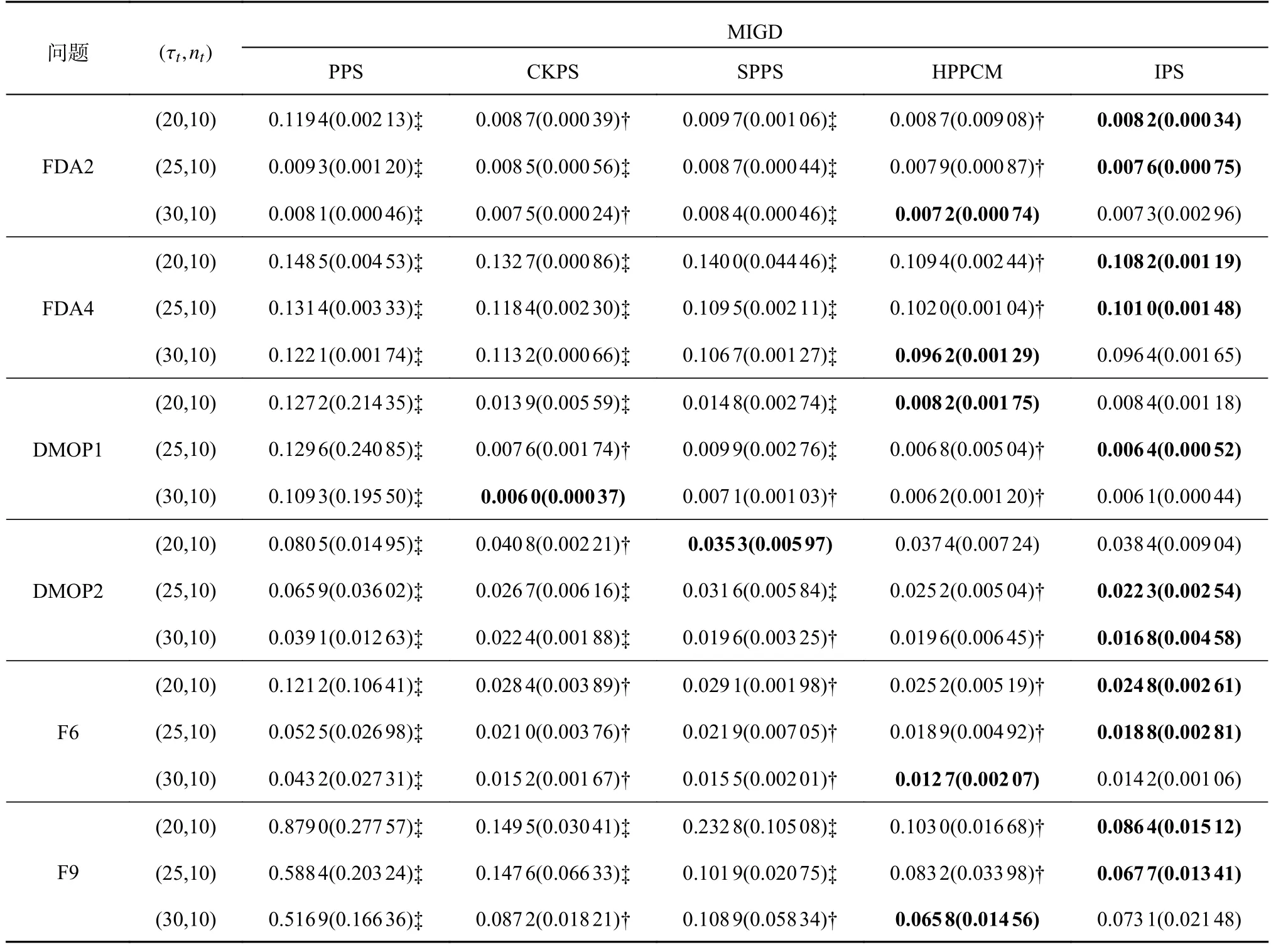
表4 5 种策略在部分测试问题上的MIGD 指标Tab.4 MIGD indicators of five strategies on some test questions

如表5 所示为5 种策略在6 个测试问题上对应3 种不同 τt的MHVD 指标，与表4 较为不同的是，SPPS 在DMOP1 测试问题上的3 个MHVD 指标是最优的，原因可能是MHVD 在评价算法性能时更倾向于边界解，而SPPS 在保留边界解的方面做得更好.

表5 5 种策略在部分测试问题上的MHVD 指标Tab.5 MHVD indicators of five strategies on some test questions

4.3 获得的解集分布图对比

为了进行更加直观的比较，选择DMOP2、F9 这2 个具有代表性的测试问题来绘制5 种策略在不同时刻所获得解集的分布图，如图6、7 所示.图中，横纵坐标表示所获得解集在不同目标上的目标值，圆点表示获得的解集，曲线表示标准PF.可以看出，对比结果与表2、3 的相同，在早期阶段，IPS 所获得的解集具有更好的收敛性和分布性，说明IPS 可以快速地响应环境变化.在后期阶段，IPS 在环境多次变化后仍能较为准确地追踪到新解，最终得到收敛性和分布性均较好的 P S，并且，IPS 所获得的PF 和标准的PF 较接近.其他4 种策略在后期阶段的表现也较为不错.由图7可以看出，IPS 在处理F9 这种复杂测试问题时也有较好的表现.

图6 5 种策略在求解DMOP2 过程中所获得的解集Fig.6 Solution set obtained by five strategies in process of solving DMOP2

图7 5 种策略在求解F9 过程中所获得的解集Fig.7 Solution set obtained by five strategies in process of solving F9

5 消融实验

5.1 参考点联系算法筛选的特殊点对IPS 的影响

比较参考点联系算法筛选0 个特殊点和9 个特殊点的IPS，设筛选特殊点的个数为s,s=0 的IPS 为IPS(0)，s=9 的IPS 为IPS(9)，选择F6 和F9 作为代表问题来比较IPS(0)和IPS(9)在20 次运行中环境变化的IGD 趋势，结果如图8 所示.可以看出，IPS(9)整体的IGD 趋势低于IPS(0)的，说明其性能比IPS(0)要好，原因是引入参考点联系算法筛选的特殊点可以使种群更快速更准确地响应环境变化，同时维持了种群的多样性.

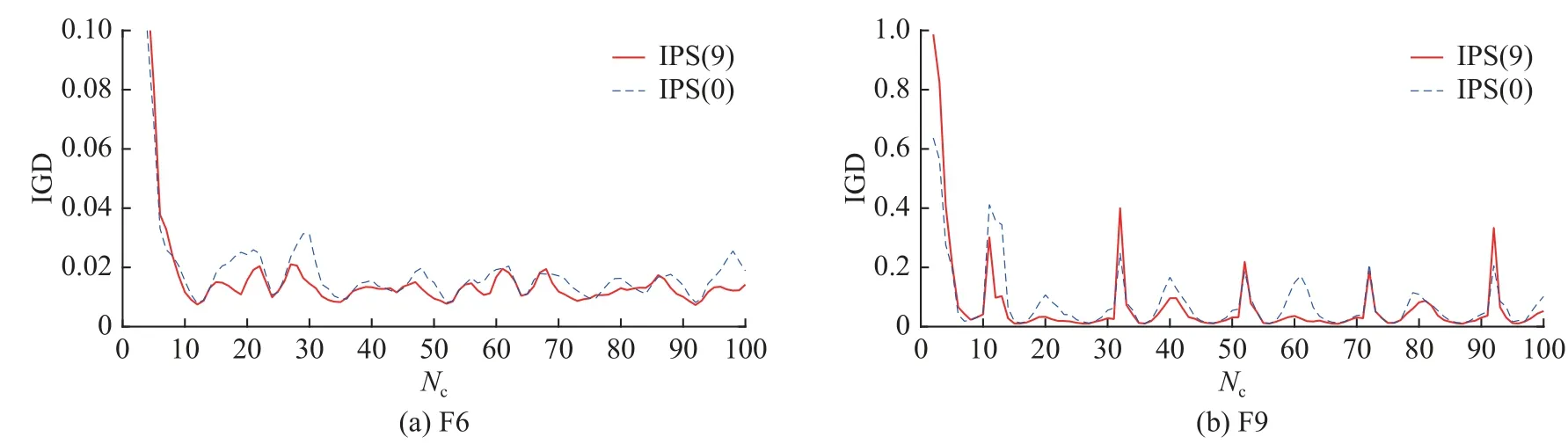
图8 IPS(0)和IPS(9)在F6 和F9 问题上运行20 次时环境变化的IGD 趋势Fig.8 IGD trend comparison of IPS(0) and IPS(9) over number of changes for 20 runs on F6 and F9

5.2 反馈校正机制对IPS 的影响

反馈校正机制是为了解决种群中心点预测方法缺乏误差反馈和校正机制，从而预测不够准确的问题.为了验证反馈校正机制对IPS 的影响，比较具有反馈校正机制和不具有反馈校正机制的IPS，设不具有反馈校正机制的IPS 为IPS(N).选择F6 和F9 测试问题来比较IPS 和IPS(N)在20 次运行中环境变化的IGD 趋势，结果如图9 所示.图中，Nc为环境变化的次数.可以看出，IPS 表现出了比IPS(N)更好的性能.原因如下：反馈校正机制校正了预测的步长和方向，提高了预测的准确性，使种群更准确地追踪新的最优解，面对复杂测试问题F9,IPS 的表现明显优于IPS(N),说明反馈校正机制应对复杂问题也较有效.

图9 IPS 和IPS(N)在F6 和F9 问题上运行20 次时环境变化的IGD 趋势Fig.9 IGD trend comparison of IPS and IPS(N) over number of changes for 20 runs on F6 and F9

6 结语

提出基于个体预测的动态多目标优化算法，种群中心点预测的非支配解集是预测种群的主体，采用反馈校正机制对其预测步长进行校正，从而更准确地追踪PF,同时引入由参考点联系算法筛选的特殊点，继而对特殊点集的预测可以快速响应环境的变化，再由混合多样性维持机制采用拉丁超立方抽样和精度可控的突变策略分别产生一部分随机个体以保持种群的多样性.选择在FDA 系列问题、DMOP 系列问题以及F5～F10 共13 个测试问题上与其他4 种算法进行比较，实验结果表明，无论是决策空间变量线性相关的问题，还是线性无关的问题，IPS 都能快速响应环境的变化，获得收敛性和多样性均较好的解集.

IPS 在应对不连续问题时有待改进，这也给未来的研究指明了一定的方向，如何在后2 个阶段延续第1 个阶段的表现将是笔者未来研究工作的重点.此外，特殊点预测策略在种群尚未收敛的时候，可能会存在预测不准确的问题，而记忆策略对PS 随时间不发生变化的问题有较好的影响，因此，将预测策略与记忆策略结合也是一项可研究的工作.