基于Mahony滤波和EKF融合的姿态解算方法*

朱 鹏，陈威平，石 颖，何林彬，谢文武，余 超

（湖南理工学院信息科学与工程学院，湖南 岳阳 414006）

0 引 言

随着通信技术的不断发展，智慧城市成为城市建设发展的潮流，室内定位是智慧城市的重要内容，是基于位置的服务的基础。室内定位技术有超宽带（ultra-wideband，UWB）［1］、WiFi［2］、低功耗蓝牙（Bluetooth low energy，BLE）［3］、超声波［4］和红外［5］等，这些技术比较依赖定位设备的布置且容易被室内环境影响。相比之下，随着微机电系统（MEMS）的发展，基于惯性测量单元（inertial measurement unit，IMU）的捷联式惯导系统使用单独的传感器实现定位［6］，不依赖其他基础设施，成为行人导航系统的理想选择。然而，从低成本的IMU 获取的数据精度有限，包含噪声，加速度计对振动噪声敏感，陀螺仪漂移严重，无法支持长时间的精确定位，在进行积分运算时，误差累积迅速，航向漂移严重。

行人姿态和航向的确定需要通过融合传感器数据，常用的传感器数据融合方法有扩展卡尔曼滤波（extended Kalman filtering，EKF）和互补滤波（complementary filtering，CF）［7］。EKF是基于卡尔曼滤波（Kalman filtering，KF）解决非线性问题的算法，EKF 和行人零速检测为框架的数据融合算法通过引入速度和角速度观测量，将误差重置，是一种能有效降低误差积累的姿态解算方法［8］。在此基础上，融合磁力计对航向校正有一定的积极作用，但由于室内磁场干扰严重和磁力计自身误差，在融合之前必须对磁力计数据进行分类，提取可用的磁场数据［9］。另一种解决航向漂移的方法是启发式漂移减少（heuristic drift reduction，HDR）［10］，在仅使用IMU的情况下，将当前解算角度与前一时刻比较，忽略小于角度阈值的姿态变化，能有效修正简单路线，但在复杂路径中修正效果并不明显。另外，噪声符合高斯分布的假设是基于EKF的融合算法的主要限制，虽然噪声协方差矩阵自适应估计已经可以解决这个问题［11］，但计算量太大，很难应用于低成本和低功耗产品。Mahony R等人提出一种显式互补滤波器［12］，只使用IMU数据估计偏差，Madgwick S O H等人提出滤波器是基于Mahony滤波实现［13］，在算法中使用梯度下降法计算姿态误差。这两种算法相较于自适应噪声估计的EKF，在计算量上会减少，但估计精度略有不足，且在干扰发生变化的动态环境中，适应力较差。

本文在仅使用IMU且不应用HDR算法的情况下，提出了一种基于Mahony 滤波和EKF 融合的姿态估计算法，首先使用Mahony滤波对IMU数据进行初步融合，得到行人在导航坐标系的加速度，将其与捷联惯导算法解算的加速度做差，作为EKF的一个观测量，再根据行人运动特征，在行人运动零速区间增加速度和角速度2 个观测量，而在非零速区间观测量仅为2 个加速度之差。经过实验证明，与单独两种滤波器相比较，在计算量较少的情况下，航向漂移更小，具有更高的精度。

1 算法框架

本文融合算法与基于行人零速区间校正误差的EKF算法框架的不同之处在于，该算法基于Mahony滤波能在运动全程中都对行人姿态进行误差校正，不仅仅局限于零速区间。在非零速区间以Mahony 滤波加速度与捷联惯导姿态解算的加速度之差作为EKF的观测量，在零速区间除了两加速度之差外，可再引入行人速度和陀螺仪输出角速度作为观测量，达到Mahony滤波和EKF融合的效果，得到行人位置。基本框架如图1所示。

1.1 姿态解算

在行人室内定位系统中，首先要将传感器所在的载体坐标系（b系）数据转换至导航坐标系（n系），行人姿态航向可以使用四元数等参数表示。

四元数表示为

式中i，j，k为单位向量，规范化四元数满足

规范化四元数可用于描述刚体旋转，绕η 旋转θ 角可表示为

对式（3）两边求导可得

其中，ω ＝［0，ωx，ωy，ωz］，为b系的角速度矢量。

根据毕卡求解法［14］，在k时刻，四元数姿态更新方程的一阶近似算法为

式中 （Ωk×）为ω的斜对称矩阵，为

以四元数表示的b系到n系的旋转矩阵为

行人在n系的加速度可表示为

式中gn为重力加速度。

则行人速度v和位置p可通过积分得到

1.2 改进的Mahony滤波

Mahony互补滤波器是通过PI 控制器调节由加速度计提供的误差矢量修正陀螺仪解算的姿态角。误差矢量由加速度计输出和由重力加速度转换至b系的向量叉乘得到，如式（10）所示

通过PI控制器调节误差矢量，即

式中 E为调节后的误差矢量。

由于Mahony滤波器在匀速运动或静止时表现更好，考虑在运动姿态解算过程中，结合零速检测算法，行人在零速状态时，误差矢量不经过PI 控制器调节，而处于非零速区间时，误差矢量使用PI控制器调节，如式（12）所示

式中 state ＝1为非零速区间，state ＝0为零速区间。

实地测试航向对比结果和n系加速度对比结果如图2、图3所示，路径为闭合矩形。从图2 中可以看出，改进后的算法能提供更稳定和更准确的航向估计信息。图3 为解算后的n系加速度，即估计的行人加速度，X轴正方向表示行人初始位置的正前向，Y轴正方向表示行人初始位置的正右向。从图3中可以看出，当行人向前行走时，改进后算法的Y轴加速度比常规Mahony算法的Y轴加速度更小，说明行人前进时的轨迹偏航更小，同样，当行人向右行走时，改进后算法的X轴加速度更小，说明行人的相对偏航更小。

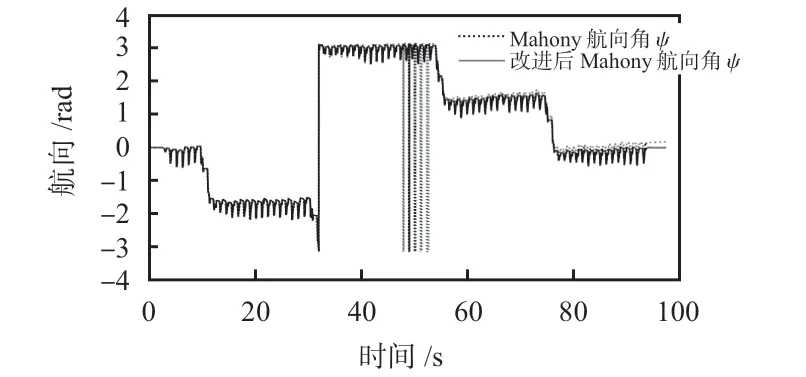
图2 航向分布

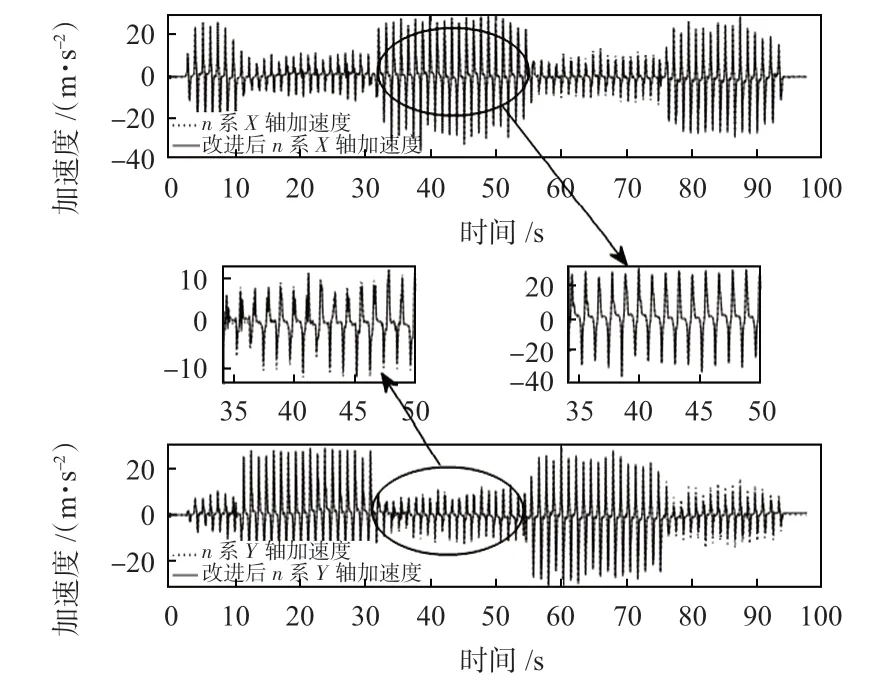
图3 n系加速度

1.3 Mahony滤波和EKF的融合

EKF是一种非线性最小方差状态估计，设离散状态空间模型如式（13）所示

式中Xk为n维状态量为n维非线性向量函数，Zk为l维量测向量，h（Xk）为l维非线性向量函数，Γk-1为系统噪声分配矩阵，系统噪声W和量测噪声V为互不相关的0均值高斯白噪声。

设已知k-1时刻Xk-1的估计值，记为，则该时刻状态真实值与其偏差为

忽略系统噪声Wk-1，则k时刻状态预测值为则状态预测值与真实值偏差为

同理，忽略量测噪声Vk-1，有，则量测预测值与其真实值偏差为

将式（13）中非线性函数f（·）和h（·）分别在和处，泰勒级数展开并取一阶近似，有

式中 J（·）为非线性向量函数的雅可比矩阵。综上，式（17）可重写为

针对式（18）所示的误差状态线性系统，可直接应用KF估计［15］。

误差状态向量如式（19）所示

式中 δφk为k时刻系统姿态误差，δωk为角速度误差，δpk为位置误差，δvk为速度误差，δak为加速度误差。

状态转移矩阵Fk如式（20）所示

其中，Sk为n系加速度构建的斜对称叉积算子矩阵

基于自适应零速检测算法，在零速区间时，速度误差δvk和角速度误差δωk为

在零速区间和非零速区间，加速度误差为

式中 上标n为由捷联惯导算法解算的n系加速度，上标m为由Mahony滤波解算的n系加速度。

零速时刻系统观测量和观测矩阵如式（24）所示

非零速时刻系统观测量和观测矩阵如式（25）所示

算法主要步骤如下，Q为过程噪声协方差阵，R为量测噪声协方差阵：

系统状态一步预测

一步预测误差协方差矩阵

卡尔曼滤波增益

简化系统状态更新过程，利用各观测量融合传感器信息

系统误差协方差阵更新

2 实验结果

实验使用的传感器模块固定在行人右脚脚背，使用MPU9250惯性传感器，通过NRF52832 MCU采集原始数据，采样频率为100 Hz，再通过串口将数据上传至PC 端，使用MATLAB软件验证该算法的可行性和有效性。

针对IMU数据中大量高频噪声，对原始数据使用巴特沃斯低通滤波器初步处理。实验中，行走路径为起点和终点在同一位置的矩形，总距离约为111 m。性能评价指标使用闭合误差ec和各采样点的欧氏距离d描述解算轨迹与参考轨迹的闭合度和契合度，如式（31）所示

式中E和S分别为实验解算轨迹的起点和终点，起点坐标为（0，0），Ld为实验参考距离，（xi，yi）为解算轨迹的采样点坐标，（Rxi，Ryi）为离散化后参考轨迹的各点坐标。

图4 为行走状态下不同算法的解算轨迹，其中黑色轨迹为参考轨迹。图5 为不同算法与参考轨迹的距离误差，先根据原始数据将参考轨迹数据离散化，再计算各采样点的距离误差，计算时去掉了行走前后静止时的采样数据。在相同条件下，本文的融合算法的解算轨迹与参考轨迹的契合度最高，在不使用HDR 算法校正航向的前提下，航向约束上依然能保持较好的性能。基于零速检测和零角速度检测算法的EKF 在航向约束上比Mahony 滤波更优，但是仅在零速区间校正误差，而在非零速区间缺少观测量，无法校正，航向漂移仍然比较严重。根据图5 给出的距离误差结果，本文算法与EKF、Mahony 滤波算法相比，平均定位误差分别降低了73.27%和78.94%。各算法闭合误差如表1所示。

表1 行走状态闭合误差%

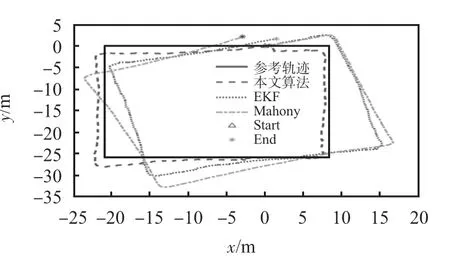
图4 行走状态解算轨迹

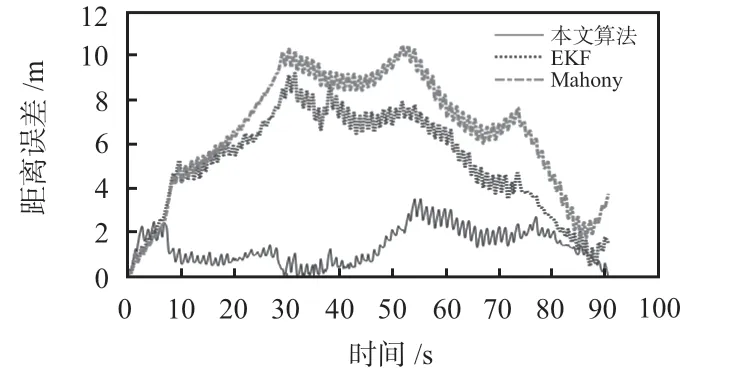
图5 行走状态距离误差

图6为慢跑状态下不同算法的解算轨迹。同等条件下，本文算法与参考轨迹的契合度更高，而EKF实际上的轨迹形状解算效果较好，轨迹闭合度达到了0.31%，但偏航严重，在行人速度较快的情况下，在零速区间的时间短且传感器输出数据与零值相差较大，行人晃动和振动引起的偏差仅在零速区间不能及时的校正航向漂移，所以轨迹契合度并不高。根据图7给出的定位误差结果，本文算法与EKF、Mahony滤波算法相比，平均定位误差分别降低了83.86%和65.76%。各算法在跑步状态下的闭合误差如表2所示。

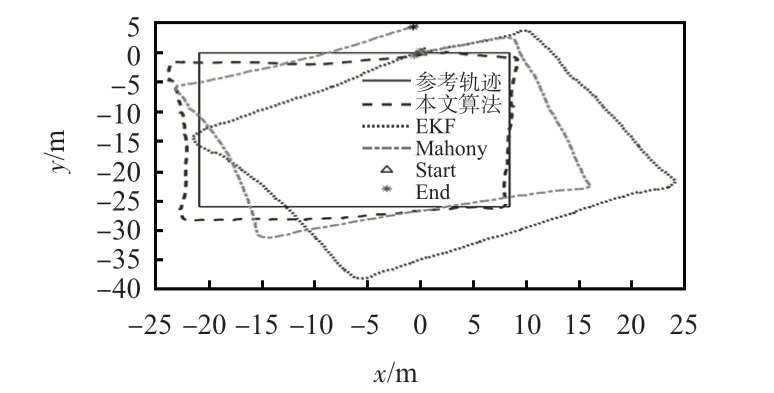
图6 跑步状态解算轨迹

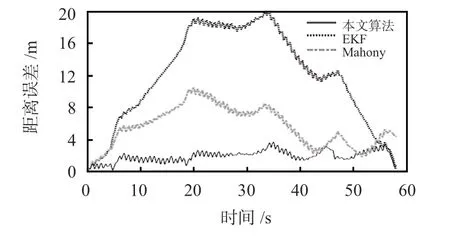
图7 跑步状态距离误差

表2 跑步状态闭合误差%

3 结 论

本文基于消费级IMU，针对其噪声大，精度低的缺点，设计了一种经过改进的Mahony滤波并结合EKF的姿态解算算法。经过实验测试，在仅有IMU 且不使用HDR 算法的情况下，该融合算法能有效降低噪声，并抑制航向漂移，能持续对行人姿态进行跟踪，重构行人轨迹，在行走状态下与EKF 和Mahony 滤波相比，平均定位误差降低了73.27%、78.94%，在慢跑状态下，平均定位误差降低了83.86 %、65. 76 %，具有更小的航向漂移和更高的解算精度。