用于移动机器人路径规划的增强型蛇优化算法*

陆顺意，何 庆，王艺蒙，李言博

（1.贵州大学大数据与信息工程学院，贵州 贵阳 550025；2.香港理工大学电子计算学系，中国 香港 999077）

0 引 言

目前，移动机器人路径规划已应用于多个领域之中，如自动驾驶、工业物流和服务业方面等。移动机器人路径规划问题作为典型的工程问题，在提升机器人定位与建图精确度方面，存在很大的探索空间。在过去的几十年里，学者们对路径规划进行了深入的研究，提出了一系列经典的路径规划方法，例如人工势场（artificial potential field，APF）法、黑猩猩优化算法（chimp optimization algorithm，ChOA）、灰狼优化（grey wolf optimization，GWO）算法、粒子群优化（particle swarm optimization，PSO）算法、被囊群算法（tunicate swarm algorithm，TSA）、鲸鱼优化算法（whale optimization algorithm，WOA）、平衡优化（equilibrium optimizer，EO）算法等［1～6］都取得了不错的效果，但仍旧存在一些缺陷。

蛇优化（shake optimization，SO）算法［7］是由Hashim F A和Hussien A G于2022年提出的一种新型的生物启发式优化算法，通过模拟蛇的觅食和繁殖行为完成寻优过程。与传统的优化算法相比，SO 算法具有原理简单、适应性好等特点。然而，SO算法同其他元启发式算法相似，普遍存在全局搜索能力差、求解精度低和收敛速度慢等缺陷。

本文提出了一种融合黄金正弦算法（golden sine algorithm，Golden-SA）［8］和莱维（Lévy）飞行［9］的SO算法（GLSOA）。首先，引入莱维飞行和非线性收敛因子，提高全局搜索效率以及平衡算法的局部开发和全局搜索能力。其次，使用局部混沌搜索策略［10］，提高算法局部开发能力。此外，还引入了Golden-SA策略，指引种群位置更新，增加迭代过程中种群的多样性，提高算法收敛速度和收敛精度。

1 地图的建立

本文基于栅格地图进行GLSOA的机器人路径规划，栅格地图建模如下：构造矩阵M，定义矩阵M中0 和1 分别表示黑色栅格和白色栅格［11］，构成Nx×Ny的二维栅格，模拟表示实际机器人移动环境，黑色栅格表示为障碍物所在区域，白色栅格为机器人可移动区域，如图1 所示，将第i个栅格位置hi坐标表示为（xi，yi），以栅格（x1，y1）处为起点，（x10，y10）为终点。

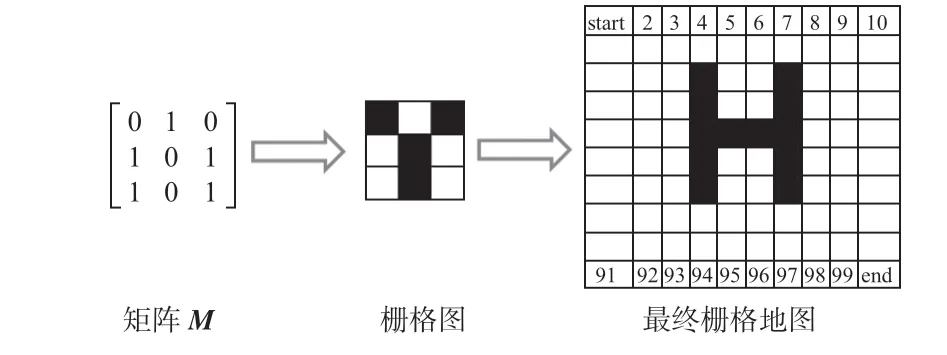
图1 栅格地图构建过程

2 GLSOA

SO的灵感来源于自然界中蛇的交配行为。如果温度低且食物充足，则会发生交配，否则蛇只会寻找食物或吃掉剩余的食物。

2.1 加入莱维飞行和非线性收敛因子

在蛇群寻找食物的全局探索阶段，通常需要对复杂的高维空间进行全局优化，以找到最优解或者近似最优解。通过引入莱维飞行机制，利用莱维飞行方向和步长的不确定性对种群位置进行扰动，提高算法的多样性，降低算法陷入局部最优的概率。同时，莱维飞行通过调整步长和跳跃方向来快速接近最优解，从而提高收敛速度。

莱维飞行的数学模型如下所示

式中 β为调整莱维飞行稳定性的重要参数，本文取1.5。

加入莱维飞行机制后，蛇群全局探索食物阶段的位置公式更新为

此外，基本SO算法的Temp收敛因子并不能提高算法收敛速度和精度，容易陷入局部最优值。针对SO 算法收敛因子下降的问题，考虑引入非线性收敛因子来改善算法的性能。同时，加入控制因子k，能控制衰减的幅度，非线性收敛因子的数学模型描述

式中t为当前迭代次数，T为最大迭代次数，Af为收敛因子的初始值，这里取1。k∈［1，10］为控制因子，k能控制A衰减幅度，k越大时收敛因子衰减越慢，反之越快。

2.2 局部混沌映射搜索策略

通过引入局部混沌映射，SO算法可以在全局搜索和局部搜索之间取得平衡，从而实现更有效的优化过程。它能够在探索性和开发性之间找到合适的权衡，既能够广泛地搜索解空间，又能够深入地探索有潜力的解。因此，将混沌映射引入SO算法可以提升算法的搜索能力和收敛性，更好地解决优化问题。

本文选取Tent混沌映射，其数学模型如下所示

式中 0 ＜α ＜1。

通过Tent混沌映射搜索策略［12］，利用混沌搜索的自适应性和伪随机性，可以使算法当前解的质量和搜索过程的进展自适应地调整搜索策略。有助于在搜索空间的不同区域应用不同的搜索策略，提高搜索效率。因此，局部开发阶段的位置更新公式为

2.3 Golden-SA策略更新位置

战斗模式中，雄性与雌性之间会相互战斗以获得最佳异性，并与之交配。这样在蛇会快速向全局最优靠近，但也会造成陷入局部最优和过早收敛的现象，难以对优质解空间进行全面探索。基于此，引入Golden-SA 策略机制可以改善交配过程中的探索方式。Golden-SA 策略数学模型描述如下所示［8］

式中Xbest为全局最优位置；r1和r2为随机数，分别决定个体位置迭代的移动距离和方向；x1和x2为黄金分割系数；黄金分割数

2.4 GLSOA实现步骤

综上改进策略，GLSOA伪代码如下：

算法1 GLSOA

1）初始化参数：种群规模N、空间维度dim、最大迭代次数T等；

2）在搜索空间内随机地初始化种群；

3）将种群N均分为雄性组Nm和雌性组Nf；

4）while（t≤T）do；

5）计算雄性组Nm和雌性组Nf的适应度值；

6）找到雄性最优个体和雌性最优个体；

7）定义温度T和食物Q，引入非线性收敛因子更新Temp；

8） if（Q＜0.25）then；

9） 全局探索阶段，寻找食物，加入莱维飞行扰动机制；

10） else if（T＞0.6）then

11） 局部开发阶段，向食物移动，引入局部混沌映射；

12） else

13） if（rand＞0.6）then

14） 进入战斗模式；

15） else

16） 进入交配模式；

17） 若选择孵化，则替换最差的雄性和雌性

18） end if

19） end if

20） 引入Golden-SA策略更新个体位置；

21）end while

22）返回全局最优解。

3 仿真实验与结果分析

仿真实验选取种群规模为30，最大迭代次数为500。为验证GLSOA在不同静态环境下机器人避障全局路径规划问题求解的寻优性能，分别选取10 ×10，30 ×30 和50 ×50的3种不同尺寸栅格环境，开展GLSOA与原SO算法和其余5个群智能算法在路径长度和寻优效率等性能提升效果实验验证。本文实验环境相关参数如表1。

表1 环境参数设置

实验结果归纳为图2、图3和表2。

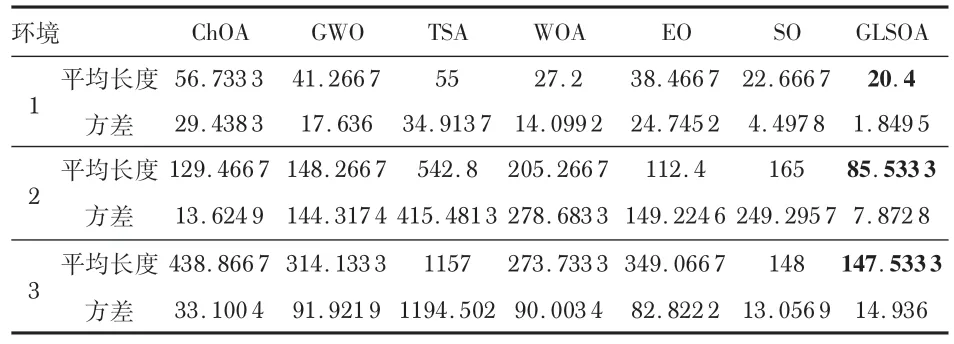
表2 基于30 次实验下不同环境中7 种算法性能对比

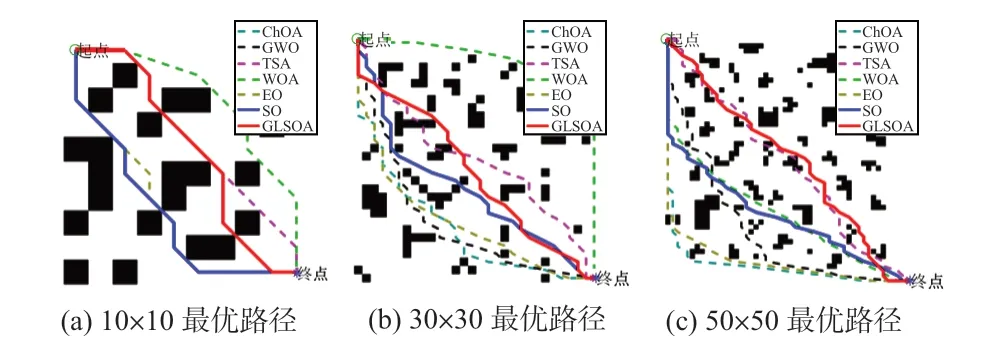
图2 7 种算法在不同规模的障碍物稀疏环境下最优路径结果

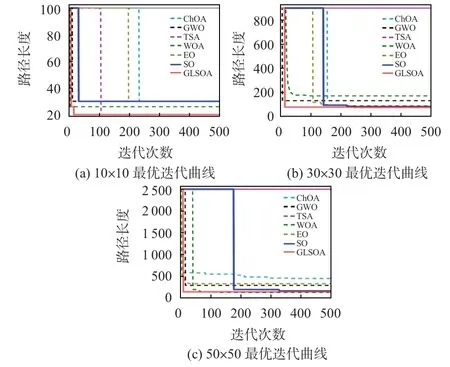
图3 7 种算法在不同规模的障碍物稀疏环境下最优迭代曲线

在图2（a）和图3（a）所示的10 ×10 地图中，本文改进的GLSOA在平均路径长度方面明显优于其他算法，相较于SO原算法长度缩短了2.27，WOA路径规划长度远远高于GLSOA，其余算法规划路径几乎一致。在图2（b）和图3（b）所示的30×30地图下，GLSOA的平均路径长度为85.533 3，较SO、EO、WOA、GWO、ChOA算法平均路径长度分别缩短79.466 7，26.866 7，119.733 4，62.733 4，43.933 4。其中，TSA路径规划失败。在图2（c）和图3（c）所示的50 ×50复杂地图中，GLSOA 算法在迭代速度和寻优精度上均优于SO原算法，最终达到优于其余所有算法的最优解。

由表2所示，GLSOA 能够在环境2 中表现出明显优势，在3个不同环境下的路径值都是最短长度，具有较好的全局搜索性能和迭代收敛能力。表明GLSOA 在机器人路径规划问题上可以获得最佳解决方案，验证了GLSOA在实际应用中的可行性和适用性。

4 结束语

本文提出了一种改进的SO 算法GLSOA，该算法弥补了原始SO算法寻优精度低、鲁棒性差、收敛速度慢等缺点。并将改进SO算法应用到栅格环境模型下的移动机器人路径规划上，仿真结果表明，融合Golden-SA和莱维飞行的GLSOA具有更好的寻优能力和鲁棒性。