法拉第反射镜温度传感特性研究

吴健华，张晓锋，陈 亮，彭 程，3，吴本祥

（1.海军工程大学电气工程学院，湖北 武汉 430033；2.92853 部队，辽宁 葫芦岛 125106；3.国防科技大学信息通信学院，湖北 武汉 430033）

0 引 言

法拉第（Faraday）反射镜作为光学系统偏振态调节器件，对提高光学系统的精度与灵敏度有着积极作用［1］，目前已经广泛应用于光纤温湿度传感［2］、光纤电流传感器［3］以及光纤陀螺仪［4］等应用领域。

由于制作工艺的限制，法拉第反射镜存在一定的制作误差，对系统产生了不利的影响。文献［5］研究了法拉第反射镜的不完善对全光纤电流传感器的影响；文献［6］分析了不完备的法拉第旋转镜对单向法拉第-迈克尔逊（Faraday-Michelson）系统的影响；文献［7］研究了法拉第反射镜不完善对连续变量量子密钥分发系统速率的影响，但以上的分析都是集中在器件制作工艺不完善，致使法拉第旋转器无法精确形成45°法拉第旋转角，而针对系统工作中无法忽视的温度效应影响则很少有文献进行研究；文献［8］虽然研究了温度对法拉第旋转器的影响，但没有给出温度对法拉第旋转器影响的机理以及对应关系。

本文从机理上解释温度影响法拉第反射镜性能的原因，构建法拉第旋转器旋转角度与温度的对应关系模型，并搭建实验系统验证分析结果，研究法拉第反射镜的温度传感特性。

1 基本原理

1.1 法拉第反射镜温度特性原理

法拉第反射镜是由法拉第旋转器和反射镜构成［3］。其中，法拉第旋转器提供恒定磁场，形成稳定的45°法拉第旋转角，基本工作原理如图1所示。

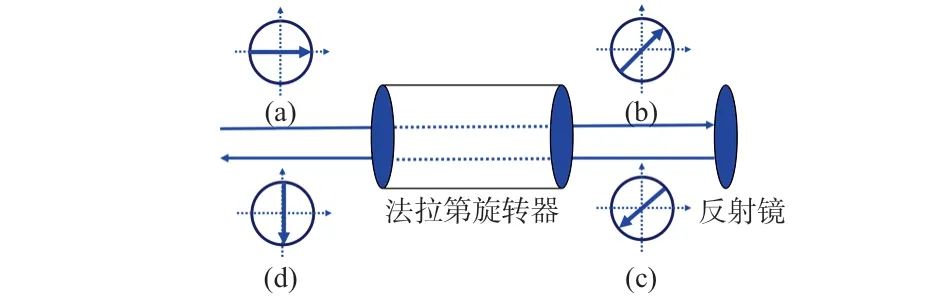
图1 法拉第反射镜基本原理示意

设入射光为水平方向的线偏振光，如图1（a）所示；通过法拉第旋转器后，偏振方向沿逆时针转45°，如图1（b）所示；经过反射镜后，由于存在半波损失，因此偏振方向反向，如图1（c）所示；最后再次通过法拉第旋转器，由于法拉第效应的非互异性，偏振方向在原有偏振方向的基础上，再次逆时针旋转45°，如图1（d）所示。此时偏振方向与入射时的偏振方向垂直。

法拉第反射镜的琼斯矩阵可以表示为

考虑温度效应时，法拉第旋转角可以表示为［9］

式中V（λ，T）为Verdet常数，与光纤的材料相关，同时与工作波长、温度有关［10］；H（T）为磁场强度，通常由磁环（永磁铁）产生；L为光束沿磁场方向的光纤长度。为形成足够大的法拉第旋转角，同时减少光纤长度，要求磁环的磁场强度足够大，目前商用的法拉第反射镜通常采用钕铁硼材料提供恒定磁场。

通过式（2）可知，当不考虑光源波长改变的情况下，温度主要影响光纤材料的Verdet 常数和磁环的磁场强度。Verdet常数的变化与温度改变量具有线性关系［11］

式中V0为室温下的Verdet 常数。当工作波长为1310 nm，V0≈1.1 ×10-6rad／A。因此，温度改变前后，Verdet常数的比值为

通过式（4）可知，当温度变化范围在100 ℃区间时，由于温度改变而影响的法拉第旋转角度改变量在10-3量级，因此，可以忽略温度对Verdet常数的影响。

当法拉第反射镜工作温度发生变化时，磁铁内部的磁畴将发生改变，永磁铁的磁场强度随之发生改变，因此法拉第旋转角度发生变化。引入剩磁温度系数作为参数。定义剩磁温度系数为

式中 Hd（T0）为开路剩磁在温度为T0时的磁信号，ΔT＝T-T0为温度变化，ΔHd为磁性变化。因此，当温度为T时，磁场强度为

式中 θT为温度为T时的法拉第旋转角。将式（7）代入式（1），则此时法拉第反射镜的琼斯矩阵可以表示为

1.2 测量系统工作原理

为准确测量法拉第旋转镜的温度性能，借鉴反射式全光纤电流传感器工作原理［12］，搭建实验系统如图2所示。

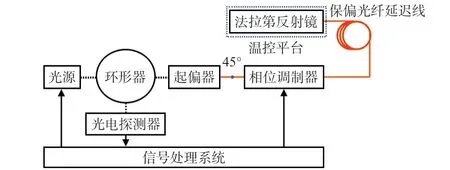
图2 法拉第反射镜温度测量原理示意

在图2中，黑色虚线表示单模光纤，用于传输能量；实线为保偏光纤，用于保持光束的偏振态；箭头表示电子信号方向。基本工作过程描述为：光源发出的光经环形器，起偏后成为线性偏振光，经过45°熔接点后，成为两束大小相等，方向互相垂直的线性偏振光。2 束线性偏振光经过保偏光纤延迟线后经法拉第反射镜进行反射，由于法拉第旋转器的作用，光束的偏振方向发生了改变，反射光携带法拉第旋转角度信息通过45°熔接点在起偏器处发生干涉，最终通过光电探测器进行能量探测。将法拉第反射镜置于温控箱内部，通过控制温度，可以确定法拉第旋转角度与温度的对应关系。为了提升系统灵敏度，引入相位调制器，采用相位调制解调方法解算法拉第旋转角。

起偏器、45°熔接点、相位调制器的琼斯矩阵分别为

式中 φ（t）和φ（t＋τ）分别为t和t＋τ时刻相位调制器所产生的相移差值。τ为光束往返通过相位调制器所用时间。

系统输出的光矢为

式中 Ein＝［Ex0Ey0］为输入光矢量。则探测器接收的光强为

式中P0为忽略了光路的损耗以及光电转换效率影响的输入光功率。通过式（11）建立了输出光强与法拉第旋转角度间的对应关系，通过式（11）和式（7），即建立了输出光能量与温度的对应关系。

设置相位调制器的调制信号为φ（t）＝［δsin（ωt）］／2，δ／2为幅值，ω为调制信号的角频率。则ωτ ＝π rad时，有

应用三角函数以及第一类贝塞尔函数［14］将式（11）展开，则

式中Jn（δ）为关于δ的n阶第一类贝塞尔函数，利用相关解调原理，则

式中J1（δ）为关于δ的一阶第一类贝塞尔函数，LPF为低通滤波运算。由式（14）可知，通过相关解调，输出电压为关于温度正弦函数。因此，通过数据拟合，可以解算剩磁温度系数，再将结果代入式（7），即可计算法拉第旋转器产生的法拉第旋转角与温度的对应关系。

2 实验系统与验证

2.1 实验系统搭建

搭建实验系统如图3 所示，虚线为单模光纤，实线为保偏光纤，箭头表示电子信号，点划线为温控平台温控管道。

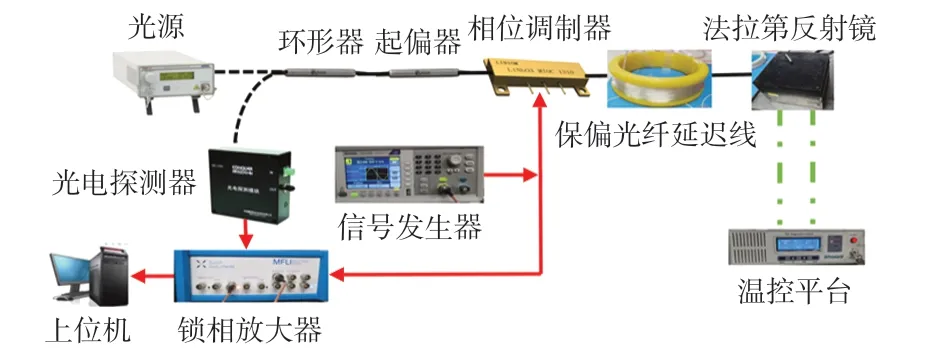
图3 实验系统

实验中，光源波长1 310 nm，谱宽45 nm，功率30 mW；环形器、起偏器以及法拉第反射镜采用深圳铭创公司的商用产品；保偏光纤应用长飞公司的保偏光纤PM1300，拍长为3 mm；相位调制器采用世维通光智能公司的直波导相位调制器，半波电压4 V，带宽50 MHz；光电探测器应用PIN-FET光探测模块，应用北京康冠的产品KG-HSP，波长1 100～1 650 nm，探测器响应度为0.9 A／W，跨阻1 200 kΩ，3 dB 带宽为10 MHz；锁相放大器500 kHz，60 Msa／s；温控平台采用武汉泰伦特世纪科技有限公司的真空高低温实验盒TLVBVHLB50，温控范围-60～100 ℃，温控精度为±0.1 ℃。

2.2 实验结果及讨论

实验过程中设置温控平台温度，从0 ℃逐渐升温至80 ℃，每次温度步进间隔为1 ℃。当测试温度达到设置温度时，持续2 min再进行数据采集，以确保法拉第反射镜受热均匀；数据采集时长为1 min，采用足够多的数据进行均值处理，以消除随机噪声的影响。通过锁相放大器获取数据与温度的对应关系如图4所示。

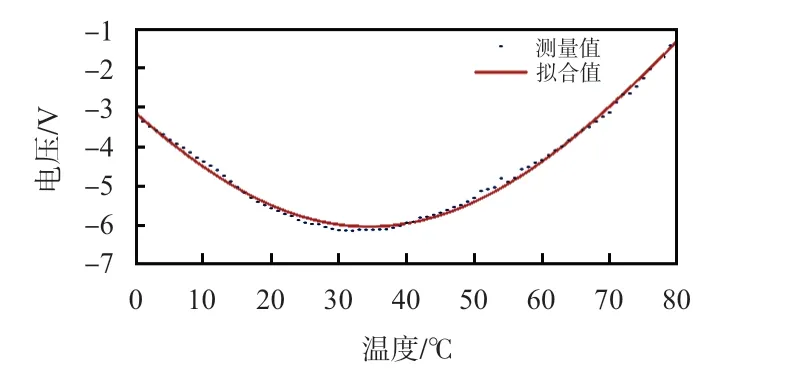
图4 实验测量结果

经计算，相关系数为0.993 9，表明拟合数据结果与测量数据具有较好的一致性。此时，数据拟合方程为

通过式（7）、式（14）、式（15）可以确定法拉第旋转镜的剩磁系数为：aT＝0.009 452。对系统的稳定性进行分析，从0 ℃开始，以10 ℃为温度间隔，最终取值到80 ℃，计算1 min内采集数据的均值与标准差数据，结果如表1所示。

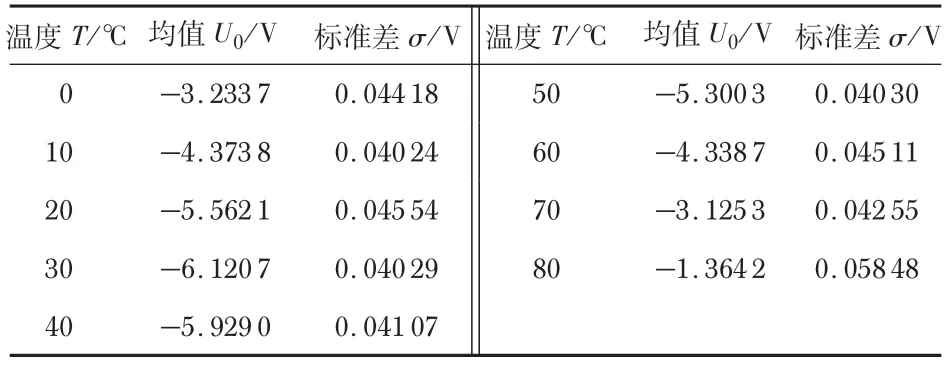
表1 不同温度时测量数据统计特性

通过表1中的标准差数据可知，采用此实验系统测量法拉第旋转角度时，实验系统具有较强的抑制干扰能力。

3 结束语

本文讨论了温度影响法拉第反射镜的主要因素，确定了温度对法拉第旋转器磁场的影响，温度对光纤的Verdet常数的影响可以忽略，并采用剩磁温度系数建立了磁场强度与法拉第旋转角度间的关系；为验证理论，搭建了反射式光学实验系统，应用相干检测算法进行系统解调，确定了输出光强与法拉第旋转角度之间的关系。通过实验证实法拉第反射镜的温度传感特性。