面向高维数据的Skyline查询处理技术研究
陈昆伦,李佳佺,李传文,邓庆绪
(东北大学 计算机科学与工程学院,沈阳 110169)
1 引 言
在大数据环境下,如何从海量数据中高效筛选出人们感兴趣的信息,是当前数据库领域关心的问题之一[1].Skyline查询可以帮助人们在大量数据中找到可能“更感兴趣”的点.Skyline查询是一个典型的多目标优化问题,在推荐系统等多标准决策场景中有许多应用.
Skyline查询是根据点间的支配关系来进行查询的,“支配关系”具体描述为:假设空间中存在两个点pi和pj,它们都有d个属性.如果pi在至少一个属性上优于pj,并且在所有其他属性上与pj一样好,则称点pi支配另一个点pj.“优于”关系通常被量化为具有较小的属性值.为了方便理解Skyline查询,本文通过一个餐厅推荐的实例加以说明,该实例如表1所示.假设某用户附近有4家餐厅,每家餐厅都具有人均消费、与用户的距离和评分等级(1是最高等级)这3个属性,餐厅推荐系统根据这3个属性为用户推荐餐厅,可以看出餐厅r2不论在人均消费、距离还是评分等级上都要优于餐厅r1和餐厅r3,因此在Skyline查询中称餐厅r1和餐厅r3被餐厅r2所支配.餐厅r4虽然在人均消费和距离上都差于餐厅r2,但其评分登记高于r2,因此餐厅r4和餐厅r2间不存在支配关系,r2和r4称为Skyline点,系统将其作为结果发送给用户.可以看出Skyline查询无法决定哪家餐馆是最适合的,而是为用户去掉各个方面都差于其它餐厅的餐厅,方便用户可以做出最终决定.
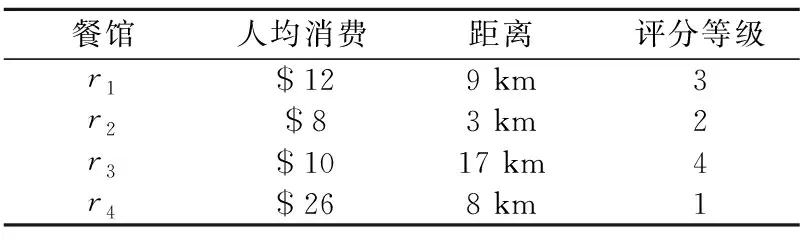
表1 餐厅推荐实例Table 1 Restaurant recommendation example
随着地理信息系统(Geographic Information System,GIS)、基于位置的服务(Location Based Service,LBS)技术和移动通信技术的高速发展,传统的Skyline查询算法出现了运行速度慢,执行效率低下等问题,因此已经无法满足不断增长的高维数据的需求[3].
顺序Skyline查算法主要包括基于排序和基于分区的两类算法.两类算法都维护一个存储Skyline点的Skyline缓冲区.基于排序的算法重新排列数据集,使Skyline点更有可能在早期被处理并添加到缓冲区中.这有助于点消除效率的提高.基于分区的算法对缓冲区中的Skyline点进行结构化,以便剩余的每个点只需要与Skyline点的子集进行比较.
Borzsonyi等人[4]提出了block-nested-loops(BNL)算法,该算法是Skyline查询的基础算法.它按顺序处理所有点,并跟踪到目前为止在Skyline缓冲区中没有被任何其他点支配的点.Chomicki等人[5]提出了排序优先Skyline(SFS)算法,该算法通过将点按曼哈顿范数进行排序来优化BNL.Sharifzadeh等人[6]提出了基于Voronoi的空间Skyline(VSS)算法,该算法在数据空间上构建Voronoi图来进行空间Skyline查询(SSQ).
现有的的研究[7,8]已经开始使用具有强大并行计算能力的GPU来进行并行化Skyline计算.大多数基于GPU的基于排序的Skyline算法[9]都是对其顺序对应的改编.这些算法将检查所有点以增加Skyline缓冲区,这阻碍了它们的效率.基于分区的并行Skyline算法使用递归分区过程或树状结构[10-13],以减少点支配检查,但它们对于GPU处理来说本质上是困难的.
针对现有方法的不足,本文提提出了基于网格划Skyline算法(SkyCell)[8],与之前的Skyline查询算法不同,SkyCell算法不是通过点与点间的支配关系,而是考虑网格间的支配关系,通过不断的对网格进行细化来得到Skyline集[9].
2 相关工作
2.1 问题定义
首先对Skyline查询设计到的相关定义进行介绍.
定义1.(点支配)任意两点p,q∈P,当且仅当满足:
1)对于任意维度k≥d,满足p[k]≤q[k]
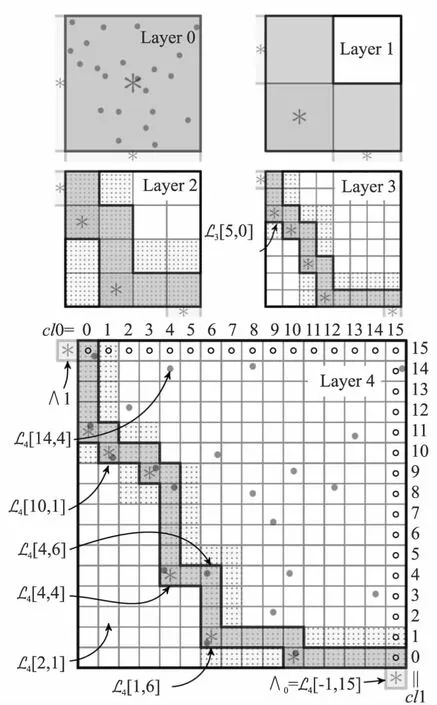
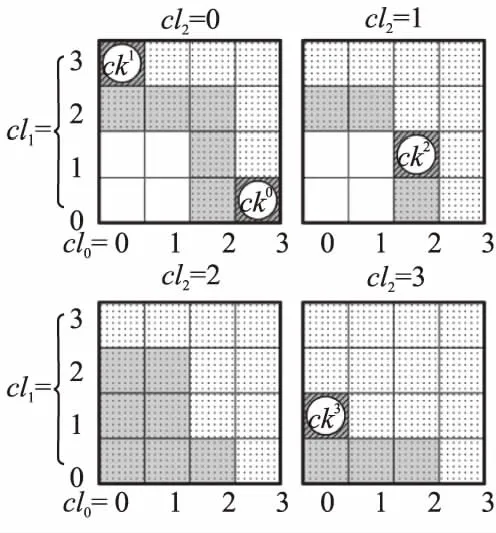
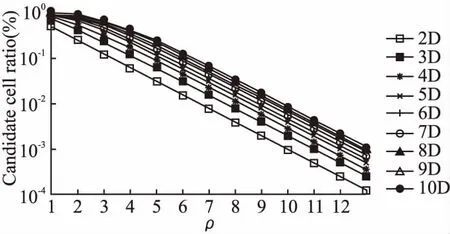
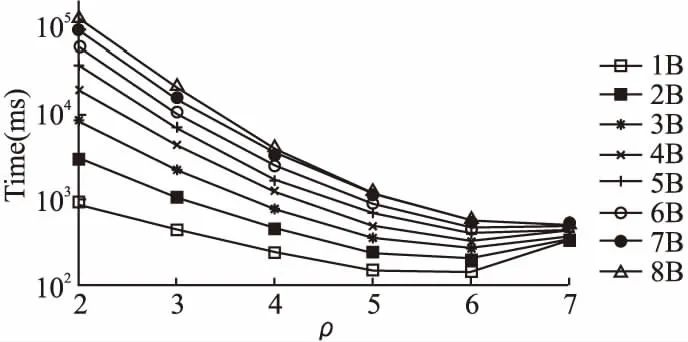
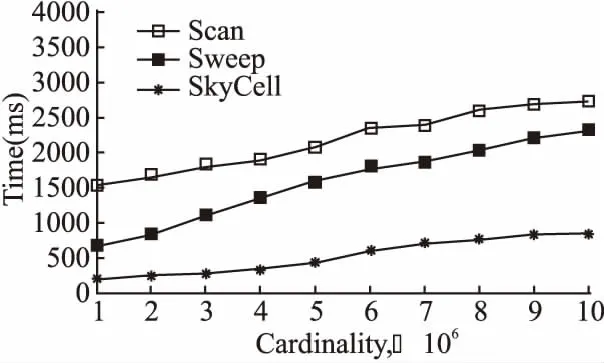
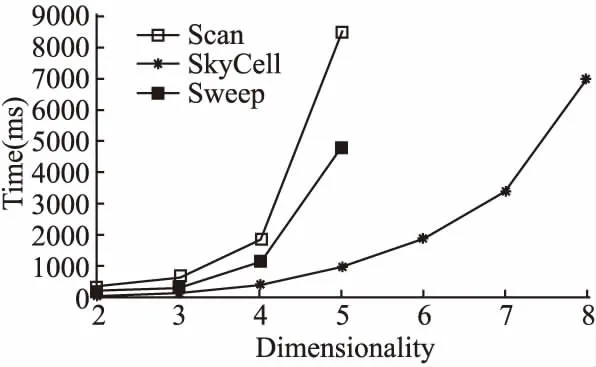
2)至少存在一个维度r≤d,满足p[r] 则称点p被点q支配,即: p (1) 定义2.(Skyline点)若点p∈P不被P中的其它任何点支配,则称点p为P的一个Skyline点. 定义3.(Skyline集)令S为所有不被其它点所支配的点的集合,即: S={p∈P|/∃q∈P:q (2) 则称S为P的Skyline集. 定义4.(Skyline查询)给定d维(d>1)欧几里得空间中n个点的集合P={p1,p2,…,pn},Skyline查询的目标是计算P中的Skyline集S⊂P. 本文将空间视为d维单元超立方体,使用多层网格对其进行划分.顶层网格层(第0层)具有最粗粒度(即整个数据空间是一个单元格),而底层(第ρ层)具有最细粒度.每一层都是一个规则的网格,在第i层有2i-d个单元.为了方便理解,给出多层数据空间划分的示例,如图1所示,其中d=2,对于第0层~第4层,有20×2=1~24×2=256个单元.每一层具有相同的单元大小.图1中将第4层放大以获得更好的可见性. 图1 多层数据空间划分示例图Fig1 Example diagram of multi-layered data space division 第i层中的单元集记为Li.单元格c=Li[cld-1,…,cl0]由其列号索引,即它分别位于维度d-1,…,0,中的cld-1,…,cl0列.使用c[k]来表示c在维度k中的索引:c[k]=clk.在图1中,第4层中的单元格c=L4[10,1]在,维度1(垂直维度)的第10列和维度0(水平维度)的第1列,即c[1]=10和c[0]=1. 在第i层中,点p所属的网格c的计算公式如公式(3)所示: cld-1,…,cl0c=Li[⎣p[d-1]·2i」,…,⎣p[0]·2i」] (3) 例如点p=(0.63,0.08)在第3层属于网格L3[|0.63×23|,|0.08×23|]=L3[5,0],在第4层属于网格L4[⎣0.63×22」,⎣0.08×24」]=L4[10,1]. 定义5.(网格支配)对同层的网格ci和cj,如果满足:ci不为空,且ci的索引在每个维度上都小于cj的索引,即: c≠Ø∧∀k∈[0,d),ci[k] (4) 则称单元格ci支配单元格cj,记为cicj. 定义6.(网格部分支配)对同层的网格ci和cj,如果满足:ci不为空,ci的索引至少在一个维度上等于cj的索引,并且ci的索引在所有其他维度上都小于cj的索引,即: c≠Ø∧∀k∈[0,d),ci[k]≤cj[k]∧∃k∈[0,d), (5) 则称单元格ci部分支配单元格cj,记为ci⪯cj. (6) 定义7.(关键网格单元)既不被任何其他单元格支配也不部分被任何其他单元格支配的非空单元格称为关键网格单元. 将第i层中所有关键单元的集合表示为Ki.图1中被“*”标记出来的网格单元就是关键网格单元. 定义8.(候选网格单元)候选网格单元由关键单元格和它们的部分支配网格单元组成,公式表示如公式(7)所示: (7) 其中,Ci表示第i层的候选网格单元集,Ki表示第层的关键网格单元集,Γ(c)表示被关键网格部分支配的单元集. 选网格单元离散化数据集P的凸包以进行Skyline计算.为了避免出错,候选网格单元必须覆盖数据空间的每个维度.为了得出候选网格单元的数量,本文使用一组覆盖每个维度的辅助候选单元.这些辅助候选网格单元的数量可以很容易地推导出来,将它们和候选网格单元建立一对一的映射关系.使用辅助关键网格单元可以简化辅助候选单元格的描述. 为了定义辅助关键网格单元,首先将d个辅助点添加到d维数据集P中.第i个辅助点λi,对于所有0≤j 辅助点虽然是Skyline点,但它们不会影响P的Skyline点.这是因为数据点落在[0,1)d中.辅助点不会支配或被[0,1)d(包括原点)中的任何点支配,这是因为它们在某些维度的坐标为1,在所有其他维度上坐标为0. 这d个辅助点在每个网格层外创造了d个额外的关键单元.这样的单元就是辅助关键单元,例如图1中每层外的浅灰色单元(第4层的∧0和∧1). 定义9.(辅助候选网格单元)第i层的辅助候选单元集合,用CcAi表示,由被辅助关键单元部分支配的网格单元组成.在d维空间第层表格中,辅助候选单元网格的数量由公式(8)计算得出: CcAi={c∈Li|c[j]=2i-1,j∈[0,d)} (8) 由于本文的算法是从候选网格单元计算出Skyline点的,候选网格单元的数量决定了计算成本,因此要对其数量进行限制. 定理1.在第i层中,候选单元集Ci和辅助候选单元集CcA之间存在双射关系. 推论1.在维d空间中,第i层中候选单元的数量,用|Ci|表示,计算公式如公式(9)所示: (9) 证明:根据定理1,候选单元格的数量与辅助候选单元格的数量相同.并结合公式(8),推导出每个j∈[0,d]的CcAi中的网格单元数,从而推导出|CcAi|和|Ci|. 1)对于j=0,有c[0]=2i-1.此情况下网格单元的数量由公式(10)计算得出: (2i-1)·2i(d-2)=(2i-1)1·2i(d-2) (10) 这些网格单元构成了[2i]d网格的一个片段,例如,二维网格中的一列(例如图1中第4层最右边的一列). 2)对于j=1,根据c[1]=2i-1和c[0]≠2i-1,以避免两次计算相同的单元.这类网格单元的数量由公式(11)计算得出: (2i-1)·2i(d-2)=(2i-1)1·2i(d-1-1) (11) 在维度0中,这些网格单元2i-1有个可能的列索引由于c[0]≠2i-1而少了一列);在维度1中,只有一个可能的列索引(c[1]=2i-1);在其他d-2维度中,每个维度都由有2i个可能的列索引(参见图1中没有第 4 层右上单元格的第1行). 3)一般来说,对于j=k,有c[k]=2i-1∧c[0]≠2i-1∧c[1]≠2i-1∧…∧c[k-1]≠2i-1.这类网格单元的数量由公式(12)计算得出: (2i-1)k·2i(d-1-k) (12) 将j∈[0,d-1]的数目相加就得出公式(9). 推论2.给定i>j,Ci中的网格单元覆盖的体积(或d=2时的面积)必须小于Cj中的网格单元覆盖的体积. 证明:直观地说,这是因为上层的候选网格单元都被下层的候选网格单元所覆盖(参考图1). 推论3.给定第i层中的一个关键单元ck让sub_cell(ck)是第i+1层中对ck进行划分后得到的单元集.在sub_cell(ck)中至少存在一个关键单元,即: ∃ck′∈subcell(ck)∧ck′∈Ki+1 (13) 证明:第i层中的每个单元,包括一个关键单元ck,在第i+1层中被划分为2d个单元,例如,图1中第0层中的一个单元在第1层中被划分为22=4个单元.因此,sub_cell(ck)≠Ø. 回顾一下,一个关键单元ck是非空的(即包含数据点),sub_cell(ck)中一定有非空的单元.在这些单元中,必须有一个单元ck′不被sub_cell(ck)中的其他单元所支配(这些单元不能都相互支配). 该推论表明第i层中的关键网格单元必须至少在第i+1层中产生一个关键网格单元. 图1中,第1层的关键单元L1[0,0](用“*”标记),产生第2层的关键单元L2[0,1],后者产生第3层的关键单元L3[0,3]. 以上就是本文提出的网格划分和候选网格单元的定义,接下将详细介绍基于此候选网格单元的Skyline算法. 基于上文介绍的网格划分和候选网格单元,本文提出了SkyCell算法,如算法1所示. 算法1.SkyCell算法 输入:数据集P 输出:Skyline点集S 1.在数据集P计算出Lρ~L0 2.R0←L0[0,…,0] 3.for i=0 to ρ-1 do 4. Ri+1=ShrinkKeyCells(P,i,Ri,Li+1) 5.return RefineSkyline(P,Rρ) SkyCell算法首先在数据集P上计算ρ层的一个网格分区.将这些点存储在一个数组中,并根据它们所属的ρ层单元进行排序,可以使用任何单元排序方法,如Z-排序,只要让同一网格单元中的点存储在数组中的一个连续段即可.然后,对于每个ρ层单元,记录该单元中的点的开始和结束数组索引.一个空单元具有相同的起始和结束数组索引.这样就构建了网格结构Lρ.从Lρ中构建出Lρ-1.对于每个网格单元c∈Lρ-1,记录下它是否包含数据点,这将用于以后的关键单元测试.重复上述过程,构建出从Lρ-2~L0的其他层的网格结构(第1行). 然后根据推论3,用一个名为单元收缩算法(ShrinkKeyCells)的子程序(第2~4行,将在后面进行详细介绍).在顺序单元收缩算法中,Ri包含关键网格单元(Ri=Ki);在此特别说明,L0只有一个网格单元、(即整个数据空间),记做K0和C0. 当Rρ被计算出来,Kρ也被计算出来.使用Kρ来计算Cρ.单元收缩算法从关键单元中计算出候选单元.然后,从Cρ中的每个候选单元中计算出Skyline点,并将它们作为结果返回.由于来自不同候选单元的点不会相互支配,候选单元可以被并行处理,本文使用排序优先的Skyline(SFS)[5]算法来计算每个单元中的Skyline点.这些步骤写于子程序RefineSkyline中(第5行). 推论4.给定一个关键单元cki+1∈Ki+1,存在一个候选单元ci∈Ci,使得cki+1∈sub_cell(ci),即: (14) 从图1中可以看出,每层的关键单元(用“*”标记)都对应于前一层的候选单元. 接下来介绍如何枚举中的候选单元.一个层中的所有单元都可以通过它们的列索引列举得出.通过仔细控制枚举过程,可以按列指数枚举一层中的所有候选网格单元.为了方便理解,枚举过程如图2所示.该图显示了3维空间的第2层网格,其中第2维(即维数d-1,是最重要的维数)由4个网格代表(可以认为它们是从cl2=0~cl2=3到的堆叠).虚线单元是从第1层的候选单元中划分出来的(即除了L1[0,0,0]之外,L1中的所有单元都是候选单元),假设第1层中只有L1[-1,-1,1]、L1[-1,1,11]和L1[1,-1,-1]3个辅助的关键单元,没有其他关键单元. 图2 枚举候选网格单元示例图Fig.2 Example diagram of candidate cell enumeration 图2中的虚线单元构成sub_cell(K1).通过列举它们来找到第2层的关键单元K2,这是通过排序从维度d-1~0的列索引来完成的,即从[0,0,0]到[3,3,3]列举[cl2,cl1,cl0].首先,考虑cl2=0.在cl1=0时,假设L1[0,0,3]被发现是第一个非空单元.根据定义,这一定是K2的一个关键单元,用ck0表示.现在cl0=3.将cl1加1(cl1=1)并重置cl0.检查到cl0=2,因为在cl0=3处已经找到了一个关键单元ck0,它将部分地支配L1[0,1,3].重复这个过程,本文列举cl1=2的单元格(cl0也等于2).没有发现非空的单元,就转到cl1=3.假设发现了另一个非空单元,即一个关键单元ck1=L2[0,3,0]. 现在转到cl2=1.再次列举[cl1,cl0].注意,cl0只需要达到2,因为存在关键单元ck0=L2[0,0,0].这就找到第3个关键单元ck2=L2[1,1,2].重复这个过程,在cl2=2时没有关键单元.在cl2=3时,有第4个关键单元ck3=L2[2,1,0].枚举结束了,因为ck3限制了cl0小于0. 上面的枚举收集了所有不被其他单元支配的非空单元,即K2中的关键单元.并且还修剪了部分sub_cell(K1)的枚举(图2中只有灰色单元被枚举),从而降低了计算成本. 接下来将介绍顺序关键单元收缩方法,该方法遵循上述思路,通过sub_cell(Ci)中的网格单元来生成Ki+1中的关键网格单元.顺序单元收缩算法如算法2所示,它列举了维度d-1~1的所有列索引组合,但是单独考虑了维度0的列索引(cl0).cl0的值范围受到Ci中候选单元的起始索引和Ki+1中找到的关键单元的约束,这样就可以对枚举的内容进行缩减. 算法2.顺序关键单元收缩算法 输入:当前层数i,关键网格单元Ki,网格单元Li+1 输出:关键网格单元Ki+1 1. Ki+1=Ø,j=0 2. for cld-1=-2 to 2i-1 do 3. … /*J表示[cld-1,…,cl1]*/ 4. for cl1=-2 to 2i-1 do 6.then 8. Gs[J]←MingS(J),Ge[J]←MinGE(J) 9. if ck=Li+1[J,-1] or c[J,2i-1] 10. 是一个辅助关键单元 then 11. Ki+1←ck,continue 12. If J不包含负索引 then 13. for cl0=Gs[J] to cl0=Ge[J] do 14. If Li+1[J,cl0]不为空 then 15. Ge[J]←cl0-1 16. If 17. NotPartallyDomed(Li+1[J,cl0]) 18. then 19. Ki+1←Li+1[J,cl0] 20. return Ki+1 使用J表示维度d-1~1的列索引组合,即Li+1[J,cl0]是被枚举单元的索引.J中每个维度的枚举从-2开始(算法2第2~第4行).这是因为辅助关键单元在第i层的索引为-1,在第i+1层加倍为-2.不是说对于一个在维度j中具有列索引clj的单元格c∈Li,sub_cell(c)包含在维度j中具有列索引从2clj开始的单元. 对于每个J,计算Gs[J]和Ge[J],以约束要枚举的cl0的值(算法2第5~第7行).如果J能形成一个辅助关键单元,则将其加入Ki+1,并进入下一个J组合(算法2第9行).如果不是,并且J不包含负指数,列举cl0来检查Li+1[J,cl0]是否为非空(算法2第10~第12行).一旦找到一个非空单元c,Ge[J]就被更新为当前的cl0-1(算法2第13行).检查c是否被Ki+1中的一个辅助关键单元所部分支配(通过NotPartiallyDomed子程序).如果不是,那么c就是一个关键单元,本文将其加入Ki+1(算法2第15行).然后进入下一个J组合(算法2第16行). 接着进一步调整Gs[J]和Ge[J],因为这些由之前的Gs[J]和Ge[J]所生成的组合产生的关键单元可能会支配或部分支配J产生的单元,这些被支配的单元可以被修剪.检查d-1个以前的索引组合,其中每个组合在一个维度上与J不同.第k个(0 本文采用C++和CUDA 10.0实现所提的算法.实验使用具有32 GB内存的64位计算机、2.1 GHz Intel Xeon Silver 4110 CPU(8核)和具有4,608核和24GB 内存的Nvidia Quadro RTX6000 GPU. 本文从OpenStreetMap[14]中获得32亿个数据点(d=2),形成一个真实的数据集,,用“OSM”表示.本文通过随机抽样创建子集,用于不同数据集基数的实验.本文通过使用前两个维度的随机采样坐标作为更高维度的坐标来进一步合成真实数据集.在之前的研究的基础上,本文还使用常用的数据集生成器[2]生成合成数据.生成的数据集包括Independent、Anti-correlated和Correlated这3部分,代表一个点在不同维度上的坐标分别是独立的、反相关的和相关的.本章使用数据维度d∈[1,10],使用数据维度n∈{1,2,…,10}×106. 将本文提出的算法SkyCell与3种最先进的算法Skyline Diagram[15]、Hybrid[16]和SkyAlign[1]进行比较. Skyline Diagram[15]是一种基于分区的顺序Skyline查询算法,该算法包含3种Skyline查询的图表象限、全局和动态Skyline.该算法通过给定一组点,将平面划分为一组区域,称为Skyline多米诺骨牌.同一个Skyline polyomino中的所有查询点都有相同的Skyline查询结果. Hybrid[16]是一种基于多核CPU的Skyline查询算法,该算法以块为单位处理点.它在所有线程之间维护一个共享的全局Skyline,用于在保持高吞吐量的同时最大限度地减少优势测试.该算法基于点的分区,在共享的全局Skyline上使用了高效可更新的数据结构. SkyAlign[1]是一种基于GPU的Skyline查询算法,该算法采用了全局静态分区方案,通过分区,我们可以允许受控分支利用传递关系并避免大多数点对点比较,优先考虑工作效率和可观的吞吐量,而不是最大吞吐量,以实现数量级更快的性能. 5.2.1 分区率ρ的影响 首先对分区率ρ的影响进行分析,以指导后续实验选择其值. 图3展示了多层网格中的第ρ层包含的候选网格的比率,其中ρ∈[1,12],d∈[2,10].请注意,该比率仅取决于层数和维度,数据集基数和分布无关.可以看出,候选单元格覆盖的空间比例随着ρ的增加呈指数下降.当d=2时,候选网格在ρ=7时覆盖不到1%的空间,并且这个比率在ρ=12时进一步下降到0.01%.当d=10时,仍然只需要ρ=10以便候选网格仅占数据空间的1%.这些结果验证了本文提出的SkyCell算法可以快速修剪大部分数据空间(以及因此的数据点),而不考虑仅考虑几层的网格. 图3 ρ与候选网格集的比率Fig.3 Ratio of candidate cells vs.ρ 图4展示了关键单元收缩时间和细化Skyline点计算时间和算法整体运行时间,其中,数据从100万(1B)~800万(8B),层数ρ从2~8.随着ρ的增加,关键单元收缩的时间增加,而Skyline点计算的时间减少,这都是符合预期的.它们的综合效果是ρ=6时的最佳总体运行时间. 图4 整体运行时间Fig.4 Overall running time 此外,随着n的增加,具有更大分层率(即更大的ρ)的网格有助于修剪更多点.因此,随着ρ的增加,数据量为8B的曲线比数据量为1B的曲线下降得更快.其他参数上的算法性能显示出类似的模式.因此,本章实验使用ρ=6作为默认值. 将顺序SkyCell算法与使用了Skyline Diagram技术的Scan算法和Sweep算法进行比较.根据Skyline图,动态设置Skyline查询,其中一个随机坐标的查询点被用作数据空间的新原点.只有右上角象限的数据点被考虑用于Skyline计算. 在每个数据集上生成nq=10,000个查询并报告平均算法响应时间.对于Scan算法和Sweep算法,由于它们需要预计算,将预计算时间摊销到算法响应时间t中,计算公式如公式(15)所示: (15) 其中,tp是预计算时间,tq是查询时间. 1)数据集基数n对顺序SkyCell算法的影响.实验结果如图5所示,n从1×106变化到10×106.可以看到SkyCell算法始终优于Scan算法和Sweep算法,且优势分别高达4倍和8倍.公平地说,这是因为Scan算法和Sweep算法的预计算时间已摊销到运行时间中.本文认为,需要大量预计算的Skyline算法在其适用性方面受到影响,因为真实数据集通常是动态的,其中更新(例如,数据插入和删除)可能会使预计算结果无效,本文提出的SkyCell算法没有这样的限制.它适用于静态和动态场景,效率很高,例如,在不到1秒的时间内从1000万个真实数据点计算Skyline点,如图5所示. 图5 数据基数n对顺序SkyCell性能的影响Fig.5 Performance of sequential SkyCell vs.n 2)数据维度的影响d对.顺序SkyCell性能的影响.实验结果如图6所示,设置d=8(d=10时算法运行时间过长). 图6 数据维度d对顺序SkyCell性能的影响Fig.6 Performance of sequential SkyCell vs.d SkyCell算法再次优于其他对比实验,且优势随着增长.这是因为,当d增加时,虽然关键网格收缩需要更多时间,但细化阶段可能需要更少的时间(因为候选单元格占用的空间更小).相比之下,Scan算法和Sweep算法需要随着d的增加以指数方式处理更多的网格,这就使得运行时间快速增加.此外,Scan算法和Sweep算法需要存储大量的预计算数据.对于d>5时,它们的预计算无法在本文实验所使用的硬件上在4小时内完成,因此在这些情况下没有报告它们的结果. 本文从网格的角度对Skyline查询进行求解,考虑网格间的支配关系,提出了基于网格收缩的算法SkyCell.本文的主要贡献如下: 1)本文提出了一种基于网格划分和候选网格的Skyline查询方法.通过使用网格支配检查,本文的方法显着减少了支配检查的数量,从而对数据集大小产生了更好的可扩展性. 2)本文提出了SkyCell算法,该算法需要检查少量恒定数量的网格,就可以产生高效的Skyline计算. 3)本文通过大量实验,从多个角度证明了本文提出算法的有效性.3 网格划分
3.1 多层网格划分
3.2 网格支配
ci[k]=cj[k]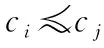
3.3 候选网格单元
3.4 限制候选单元格数量
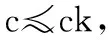
4 基于关键单元收缩的Skyline算法
4.1 SkyCell算法
4.2 单元收缩方法
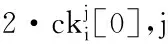
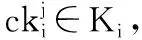
5 实 验
5.1 实验设置
5.2 实验结果分析
6 结束语

