考虑老年人满意度的社区居家养老护理人员调度问题研究

魏诗颜,梁昌勇,赵树平

(合肥工业大学 管理学院,合肥 230009)

1 引 言

目前,我国老年人口规模大,老龄化速度快,老龄事业和养老服务还存在发展不平衡不充分等问题[1].“十四五”时期,我国人口老龄化程度将进一步加深,60岁及以上人口占总人口比例将超过20%,进入中度老龄化社会[2].随着人口老龄化程度持续加深,老年人对于养老服务质量的需求也将持续增长,然而,由于当前养老服务还存在供需不匹配、保障机制不健全等问题[3],老年人的满意度难以得到有效保障.积极老龄化是应对老龄化的有效策略与选择,其实现的基础是提高老年人满意度[4].护理人员调度作为社区居家养老服务的重要一环,是提高养老服务中心服务质量,提升老年人满意度的基础[5].因此,如何在考虑老年人满意度的基础上对社区居家养老护理人员进行合理调度具有重要的研究意义.

居家养老服务中的护理人员调度问题在上世纪90年代就引起了学术界的关注.1997年,Begur等[6]首次对居家养老模式中的护理人员调度和路径规划问题进行了定义.Cheng等[7]首次使用数学工具来解决居家养老路径和调度问题.近年来,这方面的研究受到学术界更多的关注,学者们分别对不同约束进行了研究.Lanzarone等[8]考虑了护理约束的连续性,提出了不同决策模型的分配问题,主要目标是平衡某一特定类别的护理人员的工作量.袁彪等[9]将护理人员服务路线优化问题的约束主要分为了两类:服务人员最大服务能力和客户最迟开始服务时间,建立了一个以运营成本最小化为目标的家庭护理服务人员调度模型.Decerle等[10]分别对硬、软患者时间窗和同步约束条件下的问题进行了研究,建立了一个最小化惩罚成本和总旅行时间的混合整数规划模型.陶杨懿等[11]从服务时间窗、同时服务需求、医护人员技能等级与顾客需求的匹配程度等方面出发,提出以最小化的运营成本为目标的数学模型.Ettazi等[12]同时考虑时间窗、服务优先级、同步访问和午休约束,提出了一种混合算法,以优化整体成本和患者满意度.

社区居家养老服务调度问题本质上属于带时间窗车辆路径问题(Vehicle Routing Problem with Time Window,VRPTW)的扩展[13],求解算法包括精确算法和智能算法.Qureshi等[14]提出了一种基于列生成的精确优化方法,用于求解具有半软时间窗的车辆路径调度问题.Errico等[15]将具有硬时间窗和随机服务时间的车辆路径问题作为一个涉及两个阶段的先验优化问题进行研究,并使用精确的分支定价算法对其进行求解.在小规模算例中,精确算法可以在可接受的时间范围内求解出问题的最优解.但是,随着问题的复杂性和调度任务难度的增加,传统精确算法的求解时间将会呈现出指数级的增长趋势.近年来,人工智能不断发展,智能算法[16-18]也被应用到调度问题的研究中,并取得丰富成果.粒子群优化(Particle swarm optimization,PSO)算法具有简单易行、收敛速度快和设置参数少等优势,已经成为现代优化方法领域研究的热点[19].Ning等[20]提出一种结合三次样条函数的粒子群优化算法,设计了特殊的初始化策略和惩罚函数策略.陈魁等[21]将粒子群算法与小生境技术相结合求解多目标调度问题,并考虑了运输时间对粒子初始解质量的影响.Saez等[22]考虑了不同配置的粒子群优化和遗传算法,用于求解非线性混合整数优化问题,结果表明,PSO算法比基于遗传算法的算法效率更高.

此外,老年人是接受服务的主体,老年人满意度也是在该问题中需要重点关注的一个因素.近年来,大量国内外的学者对车辆路径优化问题中的客户满意度进行了深入研究.Fan[23]研究了基于客户满意度的同时取货和交货的车辆路径问题,用时间窗的下界来反映服务质量,认为顾客满意度与车辆的等待时间呈现反比关系.Rabbani等[24]通过考虑客户的优先级来考虑客户满意度,以在时间窗口的下限内最小化车辆到达客户处的时间差为目标,从而尽快为客户提供服务.Wang等[25]以食品新鲜程度来度量客户满意度,提出了一个基于有形分销成本和交付产品的无形新鲜度的时间窗处理易腐性食品车辆路径问题.户佐安等[26]以服务时间和货物完好程度来对客户满意度进行度量,提出了客户满意度最大和运输成本最小的多目标优化模型,但仅对小规模算例进行了实验.上述研究为本文建立基于模糊时间窗的老年人满意度函数提供了借鉴.

综上所述,在关于社区居家养老护理人员调度问题的研究中,学者们大多以最小化运营成本,最小化护理人员工作时长和最小化护理人员旅行距离等为优化目标,考虑护理人员技能水平与老年人需求服务等级之间的匹配关系,老年人服务需求以及老年人预约服务的软硬时间窗等影响因素.但较少有研究考虑以最小化护理人员数量为优化目标,考虑基于模糊时间窗的老年人满意度的影响因素.实际上,老年人对于服务时间的要求并非完全刚性,基于硬、软时间窗的求解方法难以准确度量老年人真实的服务满意度,对服务时间窗进行模糊化处理能够更好的反应老年人的实际需求.基于此,本文针对护理人员上门进行家政服务的场景,引入基于模糊时间窗的老年人满意度函数,并考虑护理人员数量,构建了护理人员数量最小化和老年人平均满意度最大化的多目标优化模型.在标准粒子群算法的基础上,改进惯性因子取值方法,并加入大邻域搜索算子来提高算法的局部优化性能,设计出混合粒子群算法.最后,通过数值实验和算法对比检验了所提出优化模型和算法的效率,以期为社区居家养老服务中的护理人员调度提供参考依据.

2 问题描述

本文所研究的社区居家养老护理人员调度问题是指,多个护理人员从社区居家养老服务中心出发,按照优化后的服务顺序依次对老年人进行服务,以满足老年人的服务需求,服务完成后返回社区居家养老服务中心的过程.老年人的养老服务需求一般都由老年人提前预约,提前确定好服务需求的时间窗和服务时长,社区居家养老服务中心在接收到服务任务后,应当提前对护理人员进行调度安排,确定每位护理人员的行程.

由于在现实生活中,实际服务时间与预约时间窗的偏差只会导致老年人对服务的满意度下降,并不会产生实际的惩罚费用,并且基于硬时间窗、软时间窗甚至软硬结合的时间窗的求解方法都难以对老年人接受服务的真实满意程度进行准确度量,采用模糊时间窗能够更为准确地反映老年人的实际服务需求.此外,对于社区居家养老服务中心来说,在规定的工作时长内,每位护理人员的成本都是固定的,服务一定数量老年人,所需的护理人员数量越少,服务中心的成本就越低.

本文以护理人员数量最小化和老年人满意度最大化为目标建立模型.假设如下:

1)护理人员从社区居家养老服务中心出发,服务完成后又回到服务中心.

2)每位护理人员的工作时间不能超过其额定工时.

3)所有老年人都需要接受服务,一位护理人员可以服务多位老年人,但每位老年人只能由一位护理人员服务一次.

4)每位护理人员的等级相同,且在路程中的行驶速度始终保持不变,忽略行驶过程中的各种影响行驶速度的意外情况.

5)每位护理人员的服务路径仅存在起点和终点的回路,不能存在其他回路.

6)各服务点之间的行驶距离都以欧式距离计算.

7)老年人的位置坐标、需要的服务时长在护理人员出发前已经获取.

8)老年人的满意度应当大于服务中心规定的最低水平老年人满意度.

3 数学模型

3.1 符号说明

1)参数设置

n表示老年人总数,i,j为老年人编号,i,j∈[0,n],i,j=0表示社区居家养老服务中心;

m表示护理人员总数,k为其编号,k∈[1,m];

T表示护理人员额定工时,为已知特定值;

dij表示老年人i与老年人j之间的距离;

Tij表示护理人员从老年人i处到达老年人j处所需的行驶时间;

TSik表示护理人员k开始服务老年人i的时间;

Si表示老年人i需要的服务时长;

2)决策变量

xijk,yik={0,1}

(1)

xijk=1表示护理人员k从老年人i处到老年人j处,yik=1表示护理人员k服务老年人i.

3.2 引入老年人满意度

运用服务时间窗的模糊处理对老年人的真实需要进行描述,将老年人i的满意度作为其服务起始时间的模糊隶属函数,如公式(2)所示:

(2)

其中,U(TSik)为老年人i的满意度,老年人i的模糊时间窗为[EETi,ETi,LTi,ELTi]的形式,其中,ETi为老年人i预约的时间窗下限,LTi为老年人i预约的时间窗上限,EETi为老年人i允许护理人员最早提供服务的时间,ELTi为老年人i允许护理人员最晚提供服务的时间.α,β>0,表示老年人对时间的敏感系数.为保证服务质量,设定最低水平客户满意度θ,令U(TSik)≥θ,则模糊时间窗为[Inf(Ti),ETi,LTi,Sup(Ti)],其中:

(3)

(4)

当护理人员在老年人i约定的服务时间窗[ETi,LTi]内提供服务时,其满意度U(TSik)=1;否则,该老年人的满意度将会随着护理人员提供服务的时间与老年人期望接受服务的时间之间的偏差增大而减小.当护理人员提供服务的时间早于老年人允许接受服务的最早时间或者晚于老年人允许接受服务的最晚时间,则老年人满意度为0.图1为老年人满意度随服务时间变化的情况.

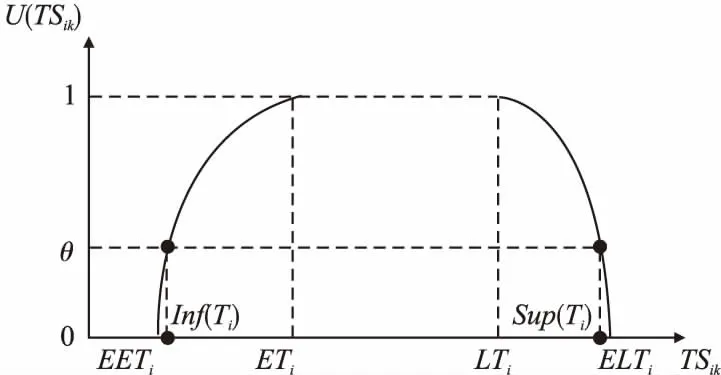
图1 老年人满意度函数Fig.1 Elderly satisfaction function

3.3 模型建立

通过以上分析,本文以护理人员数量最小和老年人满意度最大为目标函数,建立社区居家养老护理人员调度优化模型.

(5)

(6)

s.t.

(7)

U(TSik)≥θ,i∈[1,n]

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

xijk={0,1}

(17)

yik={0,1}

(18)

在上述模型中,式(5)表示最小化护理人员数量;式(6)表示最大化老年人平均满意度;式(7)表示护理人员k的工作时长不得超过规定的工作时长T;式(8)表示老年人平均满意度应当不低于最低水平服务满意度;式(9)表示护理人员k到达老年人j处的时间;式(10)表示护理人员k从老年人i处到老年人j处所需的时间;式(11)～式(13)表示每个护理人员从社区居家养老服务中心出发,服务完若干老年人之后又回到服务中心,且每个护理人员服务路径数不得超过1条;式(14)表示保证每位老年人都能被服务,且1个老年人只由1位护理人员护理1次;式(15)、式(16)表示若老年人i,j在护理人员k的服务路径上,则老年人i,j由护理人员k服务;式(17)、式(18)定义决策变量.

4 混合粒子群算法

4.1 标准粒子群算法

粒子群优化算法(Particle swarm optimization,PSO)是一种基于种群的连续优化随机算法,该算法最初是由Kennedy和Eberhart于1995年所提出[27].

PSO算法的数学表达式如下:

假定目标搜索空间为D维,一个群体中包含有N个粒子,其中第i个粒子表示为一个D维的向量:

(19)

第i个粒子的“飞行”速度也用一个D维的向量来表示:

(20)

第i个粒子到目前为止搜索到的自身的最优位置被称作个体极值:

(21)

整个粒子群到目前为止搜寻到的最优位置被称作全局极值:

gbest=(g1,g2,…,gD)

(22)

当找到这两个最优值之后,粒子根据式(23)和式(24)来更新自己的速度和位置:

(23)

(24)

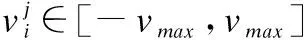
粒子群优化算法的基本工作流程如图2所示.首先对粒子群进行初始化,然后根据适应度函数的取值大小,对它们的自身和群体最佳位置进行更新.通过反复迭代,得到最优解[28].

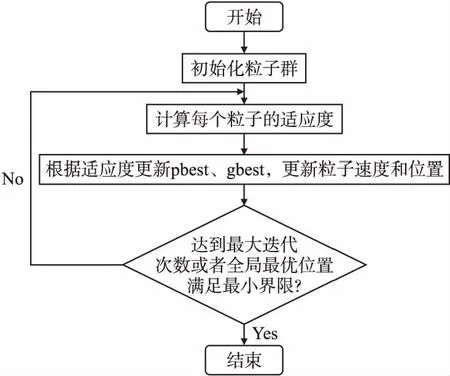
图2 粒子群优化算法流程图Fig.2 Flow chart of PSO

4.2 粒子编码

如何在求解该问题的解和粒子群优化算法的粒子之间建立一个合理的表达方式是实现PSO算法的关键.参考文献[29]的构造思路,假设本文为有nc个老年人服务点的护理人员上门服务问题,构造一个2nc维的空间,每个服务点对应两维:服务该老年人的护理人员编号为k,在相应的护理人员服务路线中,该老年人服务点的服务次序为r.为使得表达更加方便,将各个粒子所对应的2nc维向量均划分为两个nc维的向量:Xv和Xr,其中Xv表示的是每个服务点接受服务所对应的护理人员编号,Xr表示的是每个服务点在其所对应的护理人员的服务路径中的执行顺序是多少.

例如,设该问题中共有3位护理人员服务7位老年人,若某粒子的位置向量X为:

老年人编号:1 2 3 4 5 6 7

服务的护理人员Xv:1 2 2 2 2 3 3

服务次序Xr:5 3.2 6.2 1.2 2.5 0.5 4.2

其中老年人2、3、4、5都是由护理人员2进行服务,将他们对应的服务次序从小到大排序,得到护理人员2的服务路径为:首先从社区居家养老服务中心出发,为老年人4进行服务,然后为老年人5服务,再服务老年人2,然后是向老年人3提供服务,最后完成所有服务后返回到社区居家养老服务中心.如果用0表示社区居家养老服务中心,则该粒子对应的服务路径为:

护理人员1:0→1→0

护理人员2:0→4→5→2→3→0

护理人员3:0→6→7→0

粒子的位置通过解码操作转化为实际的护理人员上门服务的调度方案.

粒子速度向量V与之对应,表示为Vv和Vr.

4.3 粒子评价

在本文所提出的混合粒子群算法中,问题的解通过粒子的位置表示,即表示护理人员的服务次序.通过比较粒子的适应度函数值来反映服务次序的优劣.在判断该服务方案满足问题中的各项约束的前提下,适应度函数值越优,算法求得的解的质量越高,所得到的服务方案就越好[28].

本文将护理人员数量最小作为主要目标,老年人服务满意度最高作为次要目标,因此,适应度函数的表达式如式(25)所示:

fitness=p×m+q×[(1-U(TSik))×n]

(25)

式(25)中,fitness是指当前该粒子的适应度函数值,p、q分别表示主次目标的权重,m表示该方案中总的护理人员数量,[(1-U(TSik))×n]表示总的老年人服务不满意度.因此,适应度函数值越小,表示该方案越优.

4.4 惯性权值设计

惯性因子ω表示的是粒子能在多大程度上保留自身原来的速度,其取值越大,表明算法所具备的全局搜索能力越强,反之,其局部搜索能力就越弱.当问题空间较大时,为了权衡算法的全局搜索能力和局部搜索能力,在算法前期,通常取较大的惯性权值,有助于找到好的种子,到了算法后期,较小的惯性权值则更有助于精细搜索.因此,采用随时间变化的惯性权重取值,可以使算法获得更好的性能[30].本文采用非线性递减模型,设计惯性因子ω的取值如式(26)所示:

ω=ω0×(damp＾(gen))

(26)

其中,damp表示惯性权值衰减率,gen表示当前迭代次数,该式表明随迭代数的增大,惯性因子的取值逐渐降低,算法的局部寻优能力也随之增强.

4.5 大邻域搜索算子设计

由于粒子群优化算法存在容易陷入局部最优的问题,采用大邻域搜索算子对可行解进行指导性的破坏和修复,从而使该算法的局部优化能力有所提高.

4.5.1 破坏算子

本文采用关联度移除的方法,该方法最初是在1998年由Shaw[31]所提出,其基本原理是根据各个节点之间的相关度来移除一组点.本文通过改进该算子来解决所研究的问题,将老年人i和老年人j之间的关联程度通过R(i,j)的大小来表示,其表达式如式(27)所示:

(27)

其中:

(28)

σ={0,1}

(29)

d(i,j)表示节点i,j之间的距离,maxd(i,:)表示节点i到其余所有节点的距离最大值.σ=1表示老年人i和老年人j在同一条服务路径上.

R(i,j)越大,表示两个节点之间的关联越紧密,这意味着,更适合将它们放置在同一路径中,可以构造出更优的可行解.首先,随机选择要从原始集合中移除的一个节点,将其放入集合Removed中,然后根据该节点与原集合中其余节点的相关性由高到低排列,再依次移出需要数量的节点.

4.5.2 修复算子

本文采用距离最短插入的方法:从被移除的节点集合Removed中随机选择一个客户点removed,插入客户i和客户j之间,则总路程增量delta=d(i,removed)+d(removed,j).然后,判定当前路径是否符合该问题的所有限制条件,如果所有条件都符合,则认为该插入点是合理的,并记录下来,存储到集合outcome中.最后从合理的插入点集合outcome中选择距离增量最小的位置,即最优插入点进行插入,重复上述操作直到集合Removed为空集.若集合outcome为空集,则需要新增一位护理人员进行服务.

4.6 算法实现过程

混合粒子群算法实现步骤:

1)算法初始化.对算法中的各参数进行设定.

2)粒子群初始化.生成各个粒子的初始位置和初始速度:位置向量中,Xv∈[1,m]且为整数,其中,m表示护理人员最大数量;Xr∈[1,n]且为整数,其中,n表示老年人数量.每个粒子的速度向量中Vv∈[-(m-1),(m-1)],Vr∈[-(n-1),(n-1)].

3)初次计算各粒子的适应度函数值,确定初始全局最优配送方案.将各粒子的初始适应度函数值作为该粒子的个体最优,取gbest=min(pbest(i)),即,取所有粒子中初始适应度值最优的粒子作为初始种群中的全局最优粒子.

4)更新各个粒子的速度和位置.分别按照式(23)和式(24)进行更新,当V和X超过规定的取值范围时,按照边界值取值.

5)局部搜索.对更新后的粒子进行重定位操作,计算当前解各条路线中违反时间窗约束最大的节点,即为需要重定位的节点,然后根据距离最短插入原则将重定位的节点重新插回当前解.如果当前解中不存在违反时间窗约束的节点,则采用关联度移除的方法,依次移除需要数量的节点,最后再根据距离最短插入原则将重定位的节点重新插回当前解.

6)再次计算所有粒子的适应度函数值,更新每个粒子的个体最优位置和整个种群的全局最优位置.

7)若满足结束条件,则输出最优解,结束运行.否则转到步骤4)继续迭代.

5 算例验证

本文实验环境为:Intel(R)Core(TM)i5-10400 CPU,8.00 GB内存,Windows 10专业版操作系统,算法采用MATLAB R2018b编写.由于基于集合的粒子群优化算法(Set-Based Particle Swarm Optimization,S-PSO)能够很好的解决离散组合优化问题[32],本文选取文献[33]所提出的改进的基于集合的粒子群优化算法(Enhanced Set-Based Particle Swarm Optimization,ES-PSO)程序作为对比.

为验证模型及算法的有效性,实验中粒子数为50,c1=c2=1.49445[28],惯性因子ω采用非线性递减模型,取ω0=1,衰减率damp=0.99,护理人员工作时长为480分钟,行驶速度为50m/min,满意度时间敏感系数为α=β=1,最低水平客户满意度θ=0.75.为了简化实验,设定模糊时间窗是在算例的硬时间窗向两端进行扩展的基础上得到的,老年人允许接受服务的最早时间在硬时间窗下限的基础上提前20%,老年人允许接受服务的最晚时间在硬时间窗上限的基础上推后10%,即:

EET=ET×0.8

(30)

ELT=LT×1.1

(31)

首先采用文献[34]中服务点较少的数据,验证文中模型与算法求解问题的有效性,然后再随机选择Solomon数据集中的几个大算例进行实验.实验中,各算法均运行10次进行统计,取平均值作为实验数据进行比较.

5.1 小算例

采用文献[34]中的例子,共有1个社区居家养老服务中心和20个老年人服务点,数据如表1所示.服务点0表示社区居家养老服务中心,1～20表示老年人服务点.

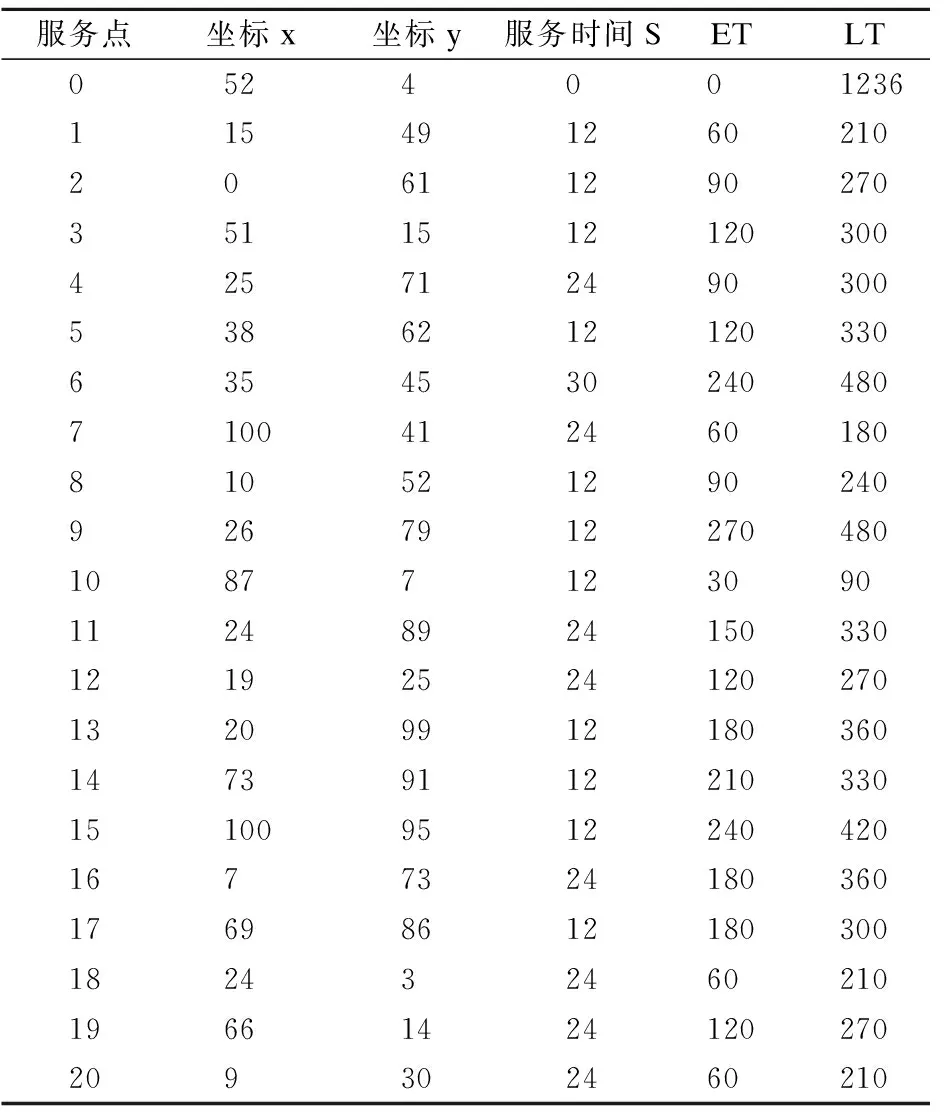
表1 服务点列表Table 1 List of service points

两种方法均进行100次迭代,运行10次取平均值,结果对比如表2所示.

表2 实验1结果对比Table 2 Experiment 1 results comparison

最优配送方案路线为:

护理人员1:

0→18→12→20→1→8→2→16→11→13→9→6→0

护理人员2:

0→10→7→14→17→4→5→15→0

护理人员3:

0→19→3→0

最高老年人平均满意度90.596%.最优配送方案路线图如图3所示.

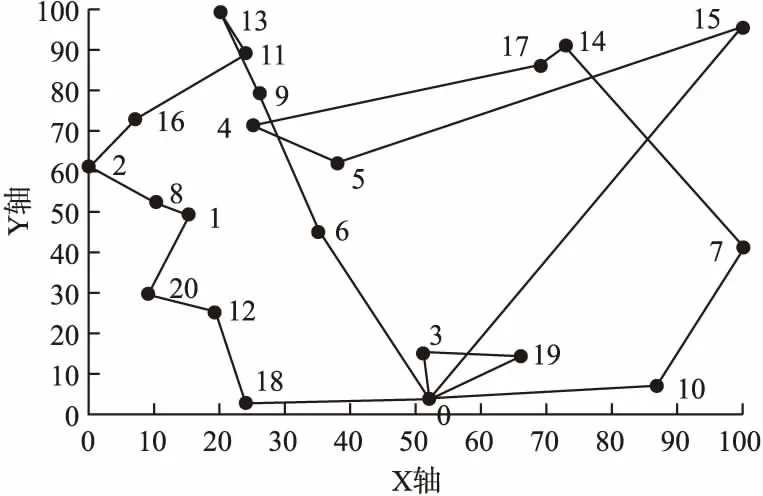
图3 最优配送方案路线图Fig.3 Optimal distribution solution roadmap

由表2可以看出,在满足最低水平客户满意度的前提下,本文提出的混合粒子群算法在护理人员数量方面比ES-PSO算法减少了1名,老年人平均满意度提高了5.603%,且平均路程减少了27.40%.

5.2 大算例

Solomon标准数据集[35]一共包含6大类:R1,R2,C1,C2,RC1,RC2.其中,R类(random)是随机分布的一组数据集,C类(clustered)则是聚集分布的一组数据集,RC类则是为部分随机部分聚集的数据集.

由于本文是针对社区居家养老护理人员上门提供家政服务,因此主要选取C类和RC类数据集进行测试.随机选择标准数据集中的C104,C204,RC104,RC204算例进行测试,增加了文献[36]中所提出的带精英策略的非支配排序遗传算法(Elitist Non-Dominated Sorting Genetic Algorithm,NSGA-II)进行对比,实验结果如表3所示.

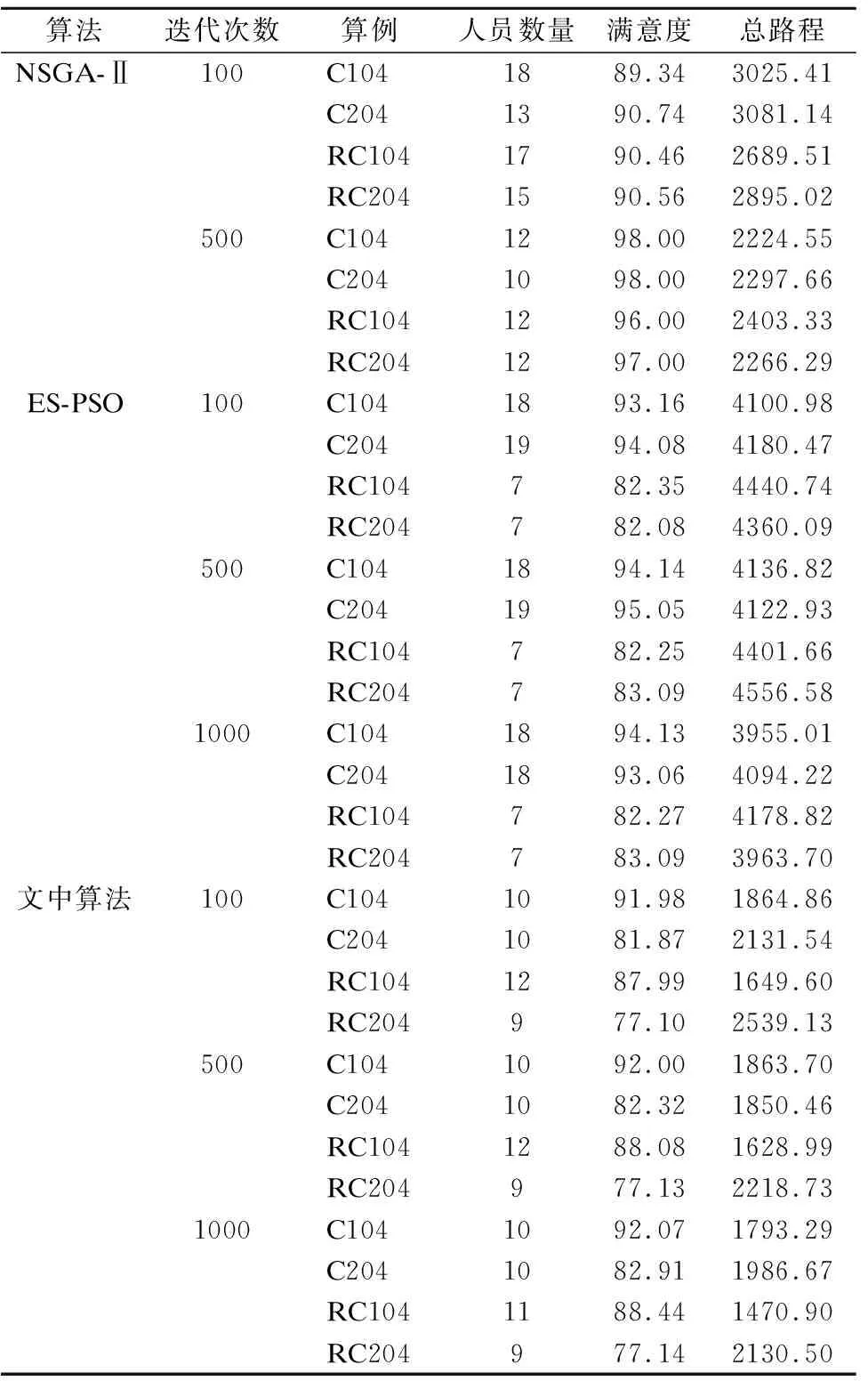
表3 实验2结果对比Table 3 Experiment 2 results comparison

由表3可以看出,随着服务点数量的增加,本文提出的混合粒子群算法优势更加明显.对比C类数据可以得出,文中算法在护理人员数量方面比NSGA-II算法和ES-PSO算法最多减少了47.37%,平均路程最多减少了55.12%,平均满意度虽然不及其他两种算法所求得的结果,但都远高于最低水平客户满意度的要求.为了更加直观的展示算法运行结果的对比情况,本文选用编写的ES-PSO算法与文中算法进行对比,分别从护理人员数量、老年人满意度和总路程3个方面绘制,如图4～图6所示.对比RC类数据可以得出,文中算法相较于NSGA-II算法仍有明显优势,在护理人员数量方面最多减少了40.00%,平均路程最多减少了38.67%.但与ES-PSO算法相比优势不太大,可知文中算法更适合求解任务点地理位置聚集分布的数据集,也就是本文中的社区居家养老背景下的护理人员调度优化问题,且平均路程最多减少了64.80%.

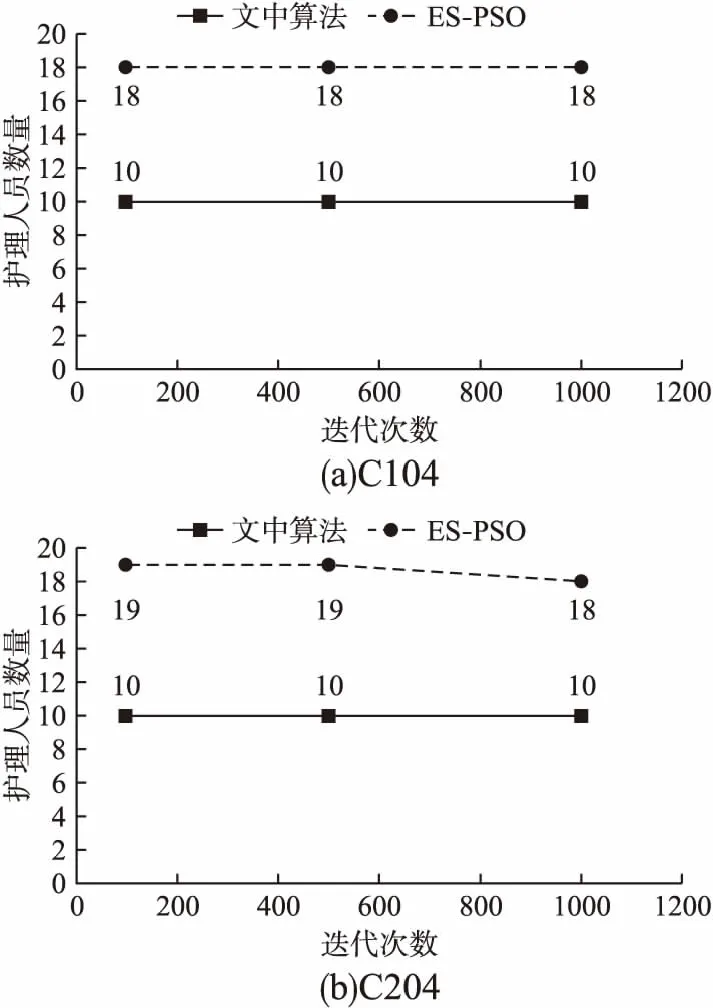
图4 护理人员数量对比Fig.4 Comparison of number of nursing staff

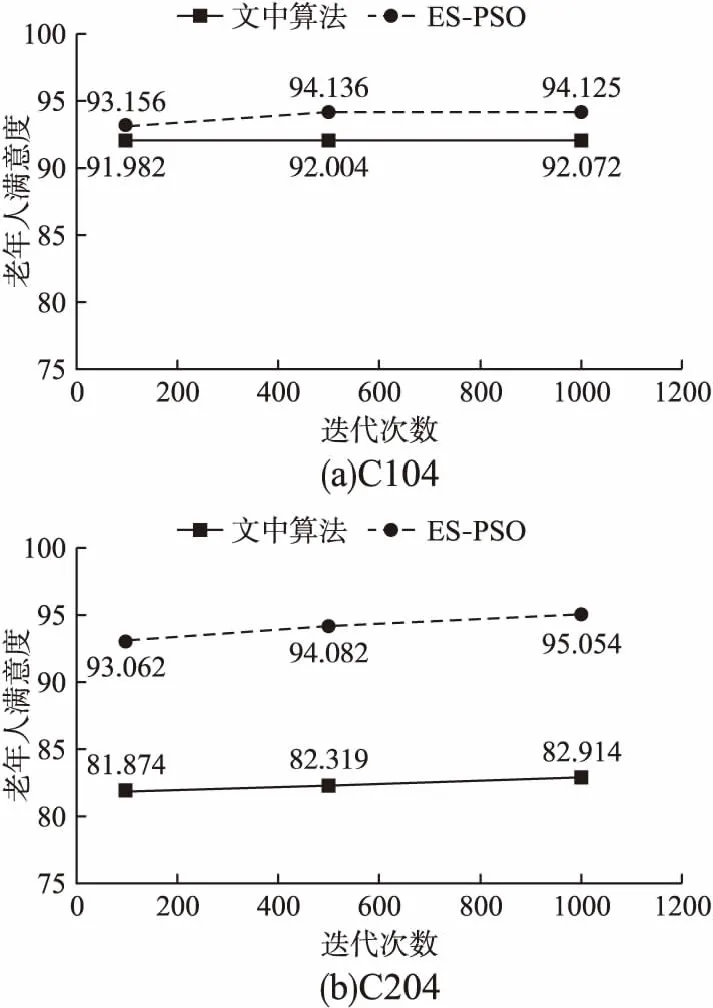
图5 老年人满意度对比Fig.5 Comparison of elderly satisfaction

6 结 论

本文对考虑老年人满意度的社区居家养老护理人员调度问题进行研究,综合考虑护理人员数量和老年人满意度两方面,建立多目标优化模型.在标准粒子群算法的基础上,改进惯性因子取值方法,并插入大邻域搜索算子,设计出混合粒子群算法对护理人员调度优化模型求解.通过对不同算例进行实验,使得所提出优化模型和算法的有效性得到了验证.实验结果表明,与NSGA-II和ES-PSO算法进行对比,本文提出的混合粒子群算法在求解老年人聚集分布的数据集中具有明显优势,能获得所需的护理人员数量更少、总路程更短的调度方案.

接下来的研究,可以在此基础上从下列几个方面入手,作更深入的研究:1)考虑护理人员从多个社区居家养老服务中心出发的情况;2)考虑老年人有多个预约时间窗的情况;3)综合考虑多个影响老年人服务满意度的因素.