频繁序列挖掘帮助的LLVM编译时能耗优化方法

阳松苡,倪友聪,2,杜 欣,2,贾建华,肖如良

1(福建师范大学 计算机与网络空间安全学院,福州 350117) 2(福建师范大学 福建省公共服务大数据挖掘与应用工程技术研究中心,福州 350117) 3(景德镇陶瓷大学 信息工程学院,江西 景德镇 333403)

1 引 言

开源编译器LLVM[1]具有高度模块化的特点和跨语言跨硬件平台的编译优化能力,现已广泛用于各类软件的开发中.LLVM提供了大量用于优化非功能性属性的编译选项并且这些选项可在编译优化过程的不同阶段被应用,进而产生不同优化效果的可执行代码.LLVM开发者虽已基于领域知识以及在典型应用和常用硬件平台下的实验结果提供了-O0、-O1、-O2和-O3(分别表示不做任何优化、基础级优化、高级优化和最高级优化)等标准优化等级,但运用这些标准等级对应的选项序列往往只能得到平均好的优化结果[2,3].

如何针对给定的硬件平台和应用程序搜索最佳LLVM选项序列以获取具有更优非功能属性的可执行代码一直是编译优化领域的公开问题和热点问题[2,3].解决这一问题将面临两个主要的挑战:一是庞大且离散的选项序列优化空间.若一个特定版本LLVM提供n个选项,规定序列长度为n(每个选项均有机会使用)并且选项可重复使用时,则由不同选项序列所构成的离散优化空间将高达nn.对于LLVM10.01中-O2等级对应序列出现的84个选项而言,其优化空间就将超过10160;二是选项之间存在复杂交互.序列中一个选项的应用可使得后续选项生效或失效,使得以不同顺序应用一组完全相同的选项可得到具有不同非功能属性优化效果的不同版本可执行代码.针对上述挑战,学术界和工业界已开展了许多LLVM编译优化研究工作.早期多以可执行代码大小或执行时间为非功能性属性优化目标,而随着物联网和云计算技术的广泛应用,有力地推动了长时间运行的嵌入式系统和数据中心应用的蓬勃发展.这些系统或应用的能耗优化[3,4]也已得到越来越多的关注.

目前国内外已涌现出机器学习[3,5]和设计空间搜索(又称迭代编译)[6,7]两类方法.然而这些方法多集中于执行时间优化,能耗优化方面开展的工作还较为稀少.与机器学习方法不同,设计空间搜索方法虽不依赖于离线预测模型或知识库而具有较好的可移植性,但在搜索过程中还缺乏有效捕获和使用选项交互信息的手段,进而影响到求解质量和收敛速度.Nobre方法[6]和Georgiou方法[7]虽依赖于标准等级隐含的选项依赖关系,但尚未考虑硬件平台和待优化应用对选项交互的影响,更未从寻优过程中动态捕获选项交互信息.而Asher方法[8]仅捕获任意两个选项之间的交互信息.另外,本文前期虽已针对GCC编译器运用频繁模式在线捕获任意多个选项之间的交互信息,提出了两种GCC编译时能耗优化遗传算法GA-FP[9]和FACET[10].但这些工作是在GCC 预定义的一组选项及其规定的使用顺序下求解选项选择的优化问题,完全不同于本文的选项序列优化问题(前者优化空间为2n而后者高达nn,假设GCC与LLVM均提供n个选项).换言之,GA-FP和FACET不适用于LLVM任意序场景下选项交互信息的捕获,因而仍需重新构建选项交互信息的挖掘模型、表示方法和挖掘算法,并在此基础上设计新的优化算法.与此同时,值得注意的是:目前仍未查阅到在迭代优化过程中动态捕获和使用与优化目标进行关联的LLVM选项交互信息的研究工作.根据大规模变量且存在变量交互的优化问题求解理论[11],这将显著影响LLVM选项序列的优化质量和寻优速度.

针对上述问题,文中提出一种频繁序列挖掘帮助的LLVM编译时能耗优化方法.该方法运用带能耗改进标注的频繁选项序列FOSE表征反复出现在优势解中的选项子序列及其功效,进一步借助不同序列长度的FOSE捕获任意多个选项之间交互并利用前缀树和后缀树进行表示;在此基础上,针对迭代寻优过程设计一种FOSE挖掘算法,从而形成可为新解生成提供有用、全面、可高效使用和时效好的选项交互信息挖掘方法;最后基于FOSE的前后缀树定义了新解生成机制并给出了新解生成的规则和过程,进而提出一种频繁选项序列挖掘帮助的LLVM编译时能耗迭代优化算法FHIA-FSM(Fast Heuristic Iteration Algorithm for energy consumption optimization under LLVM based on Frequent options Sequence Mining).考虑到Georgiou方法[7]是目前设计空间搜索方法中面向能耗优化且能最快获取较好解质量的一种LLVM选项序列优化方法,而遗传算法GA是编译优化领域公认在演化足够长时间后能获取高质量解的一种方法[12].因而,本文以Georgiou方法的优化用时和解质量分别作为基准停机时间和基准解质量,并在4个不同领域的7个典型案例下开展实验研究.统计实验结果表明:在基准停机时间下本文FHIA-FSM较Georgiou和GA的解质量平均相对改进最好可达15.52%和101.81%;在达到基准解质量的收敛速度上,FHIA-FSM较Georgiou和GA平均相对改进最好可达18.00%和25.25%.

本文的组织结构如下:第2节给出了LLVM选项序列优化相关工作;第3节阐述了FHIA-FSM算法的总体流程;第4节详细介绍了基于带能耗改进标注频繁序列的选项交互信息挖掘方法;第5节提出了带能耗改进标注频繁选项序列帮助的新解生成机制;第6节给出案例研究;第7节总结全文并给出未来工作.

2 相关工作

LLVM编译选项序列优化[2,3]作为一个公开问题一直受到高度关注,已涌现出机器学习和设计空间搜索两类主要的方法.

2.1 机器学习方法

机器学习方法[3,5]通过离线学习构建预测模型或知识库,并进一步借助优化算法获取待优化应用的最佳选项序列.这类方法已被应用于优化执行时间[13-20]和能耗[21],其可分为预测选用选项和搜索空间约简两个子类.

预测选用选项方法首先抽取各基准应用的静态[14,21]或静动态混合[13]代码特征并按一定策略对选项或选项序列空间进行迭代搜索,进而生成样本集;然后运用神经网络[13-15]和强化学习[21]等机器学习算法构建可预测当前代码特征下选用选项的模型;最后运用迭代优化算法通过重复3个步骤(抽取待优化应用代码特征、在线查询预测模型得到选用选项和施加选项到待优化应用),直至达到预设的序列最大长度或选用的选项不发生变化而停机.

而搜索空间约简方法先通过离线构建以基准应用及其最优选项序列为条目的知识库,再运用模糊聚类[16]、K近邻算法[17]、层次聚类[18]或遗传算法[19,20]选择出一组将用于待优化应用的选项或选项序列,由它们作为排序元素可形成约简后的搜索空间.进一步利用随机采样[16]、遗传算法[17,20]、推荐算法[18]或蚁群算法[19]搜索待优化应用的最佳选项序列.

机器学习方法多集中于执行时间优化.该类方法常常基于特定的硬件平台和一组特定的基准应用并以离线方式构建预测模型或知识库,当实际优化环境中的硬件平台发生变化或者被优化应用与基准应用差异较大时,离线训练方式获得的预测模型或知识库的精度都将受到较大影响,从而引发机器学习方法可移值性差的问题.

2.2 设计空间搜索方法

与机器学习方法不同,设计空间搜索方法无需离线构建的模型或知识库,而是借助已有的或在线构建的选项交互启发式信息并使用搜索算法在选项序列的优化空间中寻找具有最优执行时间[6,8]或最优能耗[7]的解.

Nobre等人[6]根据优化等级或开发者提供的选项间依赖关系构造出一种加权有向图.图中的结点表示选项,弧表示弧头选项依赖弧尾选项,而弧上的权值由依赖关系出现的次数确定.Nobre等人还基于选项依赖图提出了一种图采样生成候选解的迭代优化算法.Asher等人[8]通过在线遍历所有长度为2的选项序列,构建了选项交互的加权有向图.图中的结点表示选项,弧上标注了应用弧表示的二元选项序列可获取相对-O3等级的执行时间加速比、较单独使用弧头和弧尾选项的效果得分以及到达该弧的路径等3种信息.在此基础上,Asher等人将选项序列优化形式化为寻找哈密尔顿路径问题,并提出一种多项式时间复杂性的近似求解算法.Georgiou等人[7]以-O2等级对应序列α所确定的选项间顺序依赖关系,运用迭代删除算法从α最后一个选项开始依次剔除一个选项,并对迭代中获得的各选项序列进行能耗评估,以输出具有最优能耗的选项序列.Georgiou算法是目前设计空间搜索方法中能最快获取较好解质量的一种方法.

设计空间搜索方法多面向执行时间优化.该类方法多依赖于LLVM等级所隐含的或LLVM开发者所提供的选项交互信息,而这些信息难以适用于任意一个由硬件平台、编译器版本和待优化应用程序所构成的优化环境.另外,这类方法仍缺少捕获任意多个选项之间交互的手段.更为重要的是,目前仍未查阅到在迭代寻优过程中动态捕获和使用与优化目标定量关联的任意多个选项之间交互信息的研究工作.这从一定程度上影响了设计空间搜索方法的求解质量和求解速度.

3 频繁序列挖掘帮助的LLVM编译时能耗迭代优化算法FHIA-FSM

FHIA-FSM算法采用序列编码(xi∈{1,2,…,n})表示候选解X.其中,LLVM选项从1开始至n进行编号.FHIA-FSM算法中能耗优化目标函数fEnv(X)定义为:在给定硬件平台、LLVM和待优化应用源代码及典型输入所构成的优化环境Env下,解X相对于-O2等级对应序列获取的能耗改进百分比(降低能耗的百分比).

FHIA-FSM算法在传统迭代优化算法中融入了频繁序列挖掘方法和启发式新解生成机制,详细步骤见算法1.FHIA-FSM算法主要包括初始候选解集S生成、基于S构建初始的带能耗改进标注的选项序列事务数据库DBE、挖掘生成带能耗改进标注的频繁选项序列前缀树prefixTreeE和后缀树postfixTreeE、基于前缀树prefixTreeE和后缀树postfixTreeE的新解生成等主要步骤.

如算法1所示,第5～第9步给出了初始DBE的构建,其形式如表1所示.在传统序列事务基础上DBE中的各事务TE增加了能耗改进标注fEnv(X),从而将选项序列与其功效进行了定量关联.其可用三元组TE(tid,X,fEnv(X))进行表示,TE中各元素分别表示事务ID、选项序列(解)和能耗改进标注.进一步地,在迭代优化过程中DBE被不断更新,如第17步所示.另外,第12步的挖掘输出频繁选项序列前缀树prefixTreeE和后缀树postfixTreeE,以及第14步的新解生成将在第4和第5节进行详细阐述.

表1 带能耗改进标注的选项序列事务数据库DBE示例Table 1 Example of option sequence transaction database DBE with energy consumption improvement annotation

算法1.频繁序列挖掘帮助的LLVM编译时能耗迭代优化算法FHIA-FSM

输入:初始解集大小N,优化环境Env

输出:最优解X*

1. 迭代次数t←1;

2. 产生大小为N的候选解集S={X1,X2,…,Xi,…,XN}(1≤∀i≤N,Xk∈Ω).其中,N-1个候选解由拉丁超立方体采样产生,而另一个解为-O2等级对应的解;

3. 事务标识tID←0,DBE←Ø;//DBE初始化为空集

4.FOR(S中每个候选解Xi)DO

5. 计算Xi的目标值fEnv(Xi);//Xi较LLVM的-O2等级对应的序列能耗改进百分比;

6.IF(fEnv(Xi)> 0)THEN//有能耗改进效果,则更新DBE

7.tID←tID+1;

8. 将带能耗改进标注的选项序列事务TE(tID,Xi,fEnv(Xi))加入DBE;

9.ENDIF

10.ENDFOR

11.WHILE(未达到预设的停机时间或解质量)DO

12. 基于DBE挖掘生成带能耗标注的频繁选项序列前缀树prefixTreeE和后缀树postfixTreeE;

13.FOR(S中每个候选解Xi)DO

14. 基于Xi、前缀树prefixTreeE和后缀树postfixTreeE生成新解Yi;

15. 计算Yi的能耗目标值fEnv(Yi);

16.IF(fEnv(Yi)>fEnv(Xi))THEN

17. 在DBE中查找Xi对应的事务TE,若存在则用Yi和fEnv(Yi)分别替换TE中的Xi和fEnv(Xi);

18. 将S中Xi用Yi替换;

19.ENDIF

20.ENDFOR

21.t←t+1;

22.ENDWHILE

23. 输出S中最优解X*;

24. 结束算法运行.

4 带能耗改进标注的频繁选项序列挖掘方法

带能耗改进标注的频繁选项序列挖掘方法包括选项交互信息的挖掘模型和表示方法,以及具体的挖掘算法prefixspan+.

4.1 选项交互信息的挖掘模型和表示方法

图1给出了选项交互信息的挖掘模型和表示方法.其基于寻优过程中带能耗改进标注的频繁选项序列事务数据库DBE,并采用提出的prefixspan+算法挖掘生成带能耗改进标注的频繁选项序列前缀树prefixTreeE和后缀树postfixTreeE.选项交互信息的挖掘模型和表示方法为新解生成提供了有用、全面、可高效使用和时效性好的启发式信息.具体地:

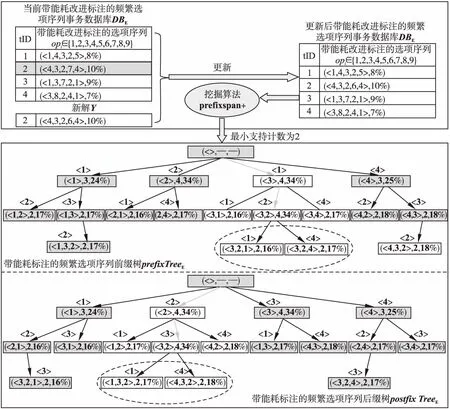
图1 选项交互信息的挖掘模型和表示方法Fig.1 Mining model and representation method for option interaction information

1)有用性

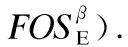
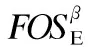
SupDBE(β)=|{TE|TE∈DBE∧β⊆TE·X}|

(1)

Eβ=∑TE∈DBE∧β⊆TE·XTE·fEnv(X)

(2)

2)全面性及可高效使用性

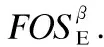
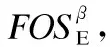
因而,将任意多个选项的频繁交互运用带能耗改进标注的频繁选项序列前缀树prefixTreeE和后缀树postfixTreeE形式进行表示.进而为选项序列寻优过程提供全面并可高效使用的启发式信息.

3)时效性

考虑到选项序列优化算法寻优过程中获取的解集在不断变化,根据生成的新解对当前数据库DBE进行更新,以保留更为优异的解,图1上部矩形框中示意了DBE的更新过程.其中:当前DBE中灰色背景指示的事务TE将被基于TE生成并且更为优异的新解Y替换.因而,从不断变化DBE挖掘出的带能耗标注的频繁选项序列可为迭代寻优过程提供最新的选项交互启发式信息.

4.2 带能耗改进标注的频繁选项序列挖掘算法

基于DBE并通过对经典和高效的prefixspan算法[22]进行扩展和改造,提出一种带能耗改进标注的频繁选项序列挖掘算法prefixspan+.

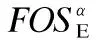
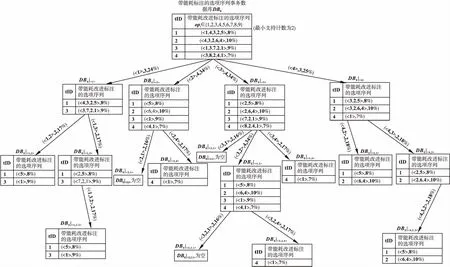
图2 以最小支持计数为2对图1中更新后数据库的递归挖掘过程示意图Fig.2 Diagram of recursive mining process after the database in figure 1 has been updated(the minimum support count is 2)

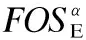
①以β=< >为前缀和α=<1>为后缀连接生成新序列γ=β°α=<1>.此时γ=α,故γ与α的支持计数和能耗改进标注相同;

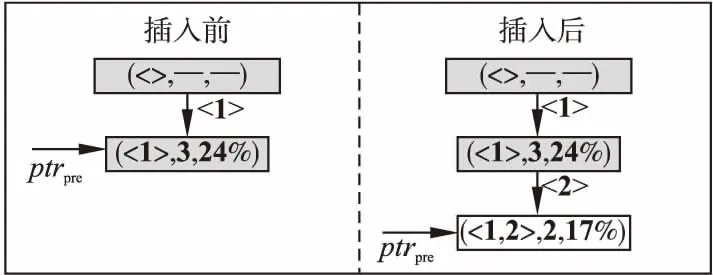
图3 插入频繁序列至前缀树之前和之后的图示Fig.3 Diagram on before and after inserting frequent

算法2.带能耗改进标注的频繁选项序列挖掘算法prefixspan+

输入:指向前缀树prefixTreeE待插入子结点的结点指针ptrpre,指向后缀树postfixTreeE根结点的指针ptrpost,频繁选项序列β,最小支持计数Supmin,以β为前缀的投影数据库DBE|β

输出:VOID

1.IF(DBE|β中事务数目小于Supmin)THEN

2.RETRUN;

3.ENDIF

4. 扫描数据库DBE|β,并在扫描过程中按式(1)和式(2)分别计算每个选项op所对应序列α=的支持计数SupDBE(α)和能耗改进标注Eα,并生成频繁选项序列集合

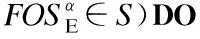
6. 生成序列γ=β°α,用于表示以β为前缀和α为后缀,并经连接生成的频繁选项序列;

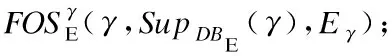
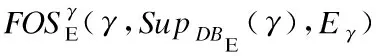
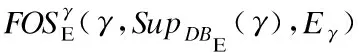
10. 构建γ的前缀投影数据库DBE|γ,其等于(DBE|β)|α;

11. 以ptrpre、ptrpost、γ、Supmin和DBE|γ为参数,递归调用prefixspan+算法;

12.ENDFOR

算法3.带能耗改进标注的频繁选项序列插入前缀树算法insertpre

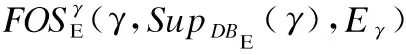
输出:待插子结点的新指针ptrpre

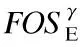
2. 在ptrpre指向结点的哈希表中增加一个表项,该表项的键值为α对应选项,值为指针ptrnewNode;

3.ptrpre←ptrnewNode;

4. 返回ptrpre;

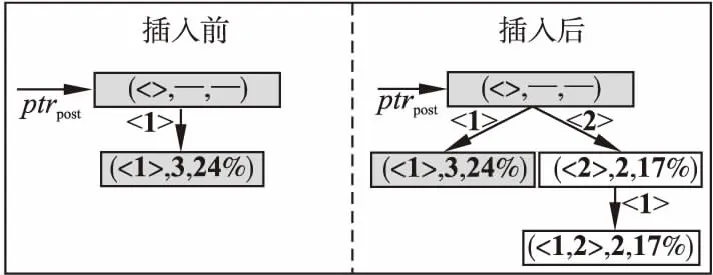
图4 插入频繁序列至后缀树之前和之后的图示Fig.4 Diagram on before and after inserting frequent

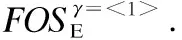
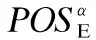
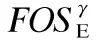
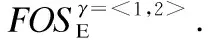
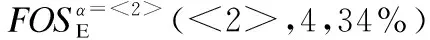
算法4.带能耗改进标注的频繁选项序列插入后缀树算法insertpost

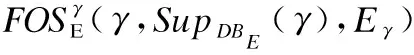
输出:VOID

1.i←序列γ的长度len,ptrpar←ptrpost;//ptrpar指示待插位置

2.WHILE(i>0)DO//逆序插入γ中各元素

3. 以γ[i]为键在ptrpar指向结点的哈希表中查找,并获取指向匹配子结点的指针ptrchd;

4.IF(ptrchd不为空)THEN//匹配成功

5.IF(ptrchd指向结点的频繁序列的支持计数小于SupDBE(γ))THEN//更新结点中频繁序列的标注

6.ptrchd指向结点对应的频繁序列的支持计数和能耗改进标注分别置为SupDBE(γ)和Eγ;

7.ENDIF

8.ELSE

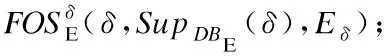
11. 在ptrpar指向结点的哈希表中增加一个表项,该表项的键值为γ[i]选项,值为指针ptrnewNode;

12.ptrpar←ptrnewNode;

13.ENDIF

14.i←i-1;

15.ENDWHILE

5 带能耗改进标注频繁选项序列帮助的新解生成机制

带能耗改进标注频繁选项序列帮助的新解生成机制以前缀树prefixTreeE和后缀树postfixTreeE作为启发式信息设计了一组与新解生成相关的规则,并进一步定义了具体的新解生成过程.

5.1 与新解生成相关的规则

下面以图1中前缀树prefixTreeE和后缀树postfixTreeE,以及解X=<5,6,3,2,7>中连续子序列α=<3,2>为例阐述前缀匹配、后缀匹配和概率选择等与新解生成相关的规则.

1)前缀匹配规则

将解X=中确定的连续子序列α=(1≤strt≤end}生成式(3)定义的选项-平均功效集Sop作为匹配结果;若匹配不成功,则将空集Ø作为匹配结果.式(3)中chd.β[end-strt+2]表示孩子结点chd中选项序列最后一个元素对应的选项op.

例中,α=<3,2>在图1前缀树中匹配获得孩子结点集Schd={(<3,2,1>,2,16%),(<3,2,4>,2,17%)},如图1中prefixTreeE虚线框中白色背景指示的两个结点,匹配路径已用灰色的弧在前缀树中标出.根据式(3)计算的匹配结果Sop={(1,8%),(4,8.5%)}.

(3)

2)后缀匹配规则

将解X=中确定的连续子序列α=(1}生成式(4)定义的选项-平均功效集Sop作为匹配结果;若匹配不成功,则将空集Ø作为匹配结果.式(4)中chd.γ[1]表示孩子结点chd中选项序列第一个元素对应的选项.

例中,α=<3,2>在图1后缀树中匹配获得孩子结点集Schd={(<1,3,2>,2,17%),(<4,3,2>,2,18%)},如图1中postfixTreeE虚线框中白色背景指示的两个结点,匹配路径已用灰色的弧在后缀树中标出.而根据式(4)计算的匹配结果Sop={(1,8.5%),(4,9%)}.

(4)

3)概率选择规则

概率选择操作根据前缀匹配或后缀匹配规则的匹配结果Sop按概率选中某个选项.具体地,若Sop=Ø,则按等概率从优化问题提供的n个选项中随机选择一个;若Sop≠Ø,则按式(5)定义的概率pj选择选项j.式(5)中j为Sop中出现的选项,而avgUtilj为选项j对应的平均功效.

(5)

例中后缀匹配规则的匹配结果Sop={(1,8.5%),(4,9%)},则选择选项1的概率p1=8.5%/(8.5%+9%)≈48.6%,而选择选项4的概率p4=9%/(8.5%+9%)≈51.4%.

5.2 新解生成过程

基于上一节设计的前缀匹配、后缀匹配和概率选择3种规则,算法5给出了新解生成过程的详细步骤.

算法5.新解生成算法

输入:解X=

输出:新解Y

1.i←随机产生0或1,Y←X;

2.IF(i==0)THEN// 按前缀匹配生成新解

3. 随机产生起始位置strt和结束位置end(1≤strt≤end;

4. 运用前缀匹配规则,并按式(3)获取匹配结果Sop(选项-平均功效集);

5. 基于Sop并运用概率选择规则,获取选中的选项j;

6. 将Y中第end+1元素更新为j;

7.ELSE// 按后缀匹配生成新解

8. 随机产生起始位置strt和结束位置end(1;

9. 运用后缀匹配规则,并按式(4)获取匹配结果Sop(选项-平均功效集);

10. 基于Sop并运用概率选择规则,获取选中的选项j;

11. 将Y中第strt-1元素更新为j;

12.ENDIF

13. 输出Y并结束算法运行;

算法5第3行～第6行给出了基于前缀匹配的新解生成过程,而第8行～第11行给出了基于后缀匹配的新解生成过程.例中X=<5,6,3,2,7>,若前缀匹配和后缀匹配两种新解生成过程中随机产生的起始位置strt和结束位置end都分别为2和3,则前者和后者获取的匹配结果分别为Sop={(1,8%),(4,8.5%)}、Sop={(1,8.5%),(4,9%)}.假定按平均功效大概率选中选项,则前者和后者都会选中选项4.因而,前者生成的新解Y=<5,6,3,2,4>,而后者对应的新解Y=<5,4,3,2,7>.

6 案例研究

本节给出了实验研究.其中6.1节简介了实验案例;6.2节给出了实验中使用的统计方法;6.3介绍了实验安装;6.4节设定了需要研究的问题,同时展示了实验结果并给出实验分析.

6.1 案例简介

通过综合考虑应用领域、源代码的结构特性和操作特性3个要素,本文从包含应用程序最多、用于嵌入式系统执行时间和能耗优化的开源基准平台BEEBS[23]中选取了7个具有代表性的应用程序作为案例,如表2所示.这些案例涵盖了安全、网络、汽车和消费4个领域,并覆盖了函数调用、嵌套循环、位操作、字符串操作、单循环和数组访问等常见源代码结构特性,同时也尽可能多地包括影响运行时能耗的整型运算强度、浮点运算强度、分支频度和内存访问频度等不同的源代码操作特性,并在表2中用“低”、“中”和“高”对强度或频度进行分级.

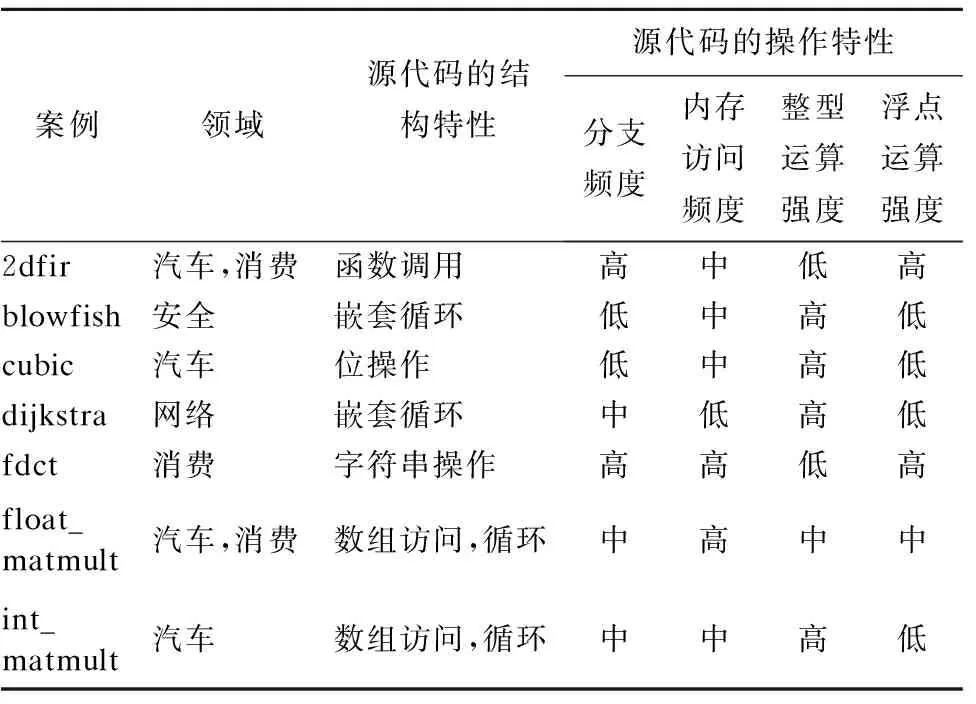
表2 实验案例的基本情况Table 2 Basic information of experimental case

6.2 使用的统计方法

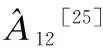
6.3 实验安装

1)实验环境

表3给出实验环境的具体配置.

表3 实验环境配置Table 3 Experimental environment configuration

2)算法参数的设定

表4给出了FHIA-FSM和GA算法下的参数设定,符号NA表示不包含对应参数.而Georgiou算法[7]不含任何参数.

表4 FHIA-FSM和 GA算法参数设置Table 4 Parameter settings of FHIA-FSM and GA algorithms

6.4 实验研究的问题、结果及分析

考虑到Georgiou算法[7]与本文FHIA-FSM算法同为基于设计空间搜索并且面向最小化能耗的LLVM选项序列优化方法,与此同时Georgiou算法也是目前设计空间搜索方法中能最快获取较好解质量的一种方法.而遗传算法GA是编译优化领域公认在演化足够长时间后能获取高质量解的一种方法[12].因而本文以Georgiou算法的优化用时和解质量分别作为停机基准时间和基准解质量,并在表2所示的4个不同领域的7个典型案例下围绕求解质量和收敛速度两个问题开展实验研究.

1)问题1(求解质量):按照基准停机时间,本文的FHIA-FSM算法较Georgiou算法和GA算法能否得到更优的选项序列,使得案例应用程序的运行时能耗更低?通过回答这一问题,可以验证FHIA-FSM算法的有用性.

表5给出了在基准停机时间下FHIA-FSM、GA和Georgiou 3种算法针对各个案例所获取最佳目标值(相对-O2等级最好的能耗改进百分比)的统计量结果.表5中FHIA-FSM同时优于GA和Georgiou的值已被加粗表示.由表5的统计量结果可知:FHIA-FSM在7个案例下最佳目标值的平均值都较GA和Georgiou更优;除fdct案例外,在其它6个案例最佳目标值的最大值中,FHIA-FSM也都较GA和Georgiou更优;FHIA-FSM在7个案例下最佳目标值的最小值也较GA更优.与此同时,GA在7个案例下最佳目标值的平均值和最小值均劣于Georgiou;除fdct、float_matmult和int_matmult 3个案例外,在其它4个案例最佳目标值的最大值中,GA也均劣于Georgiou.

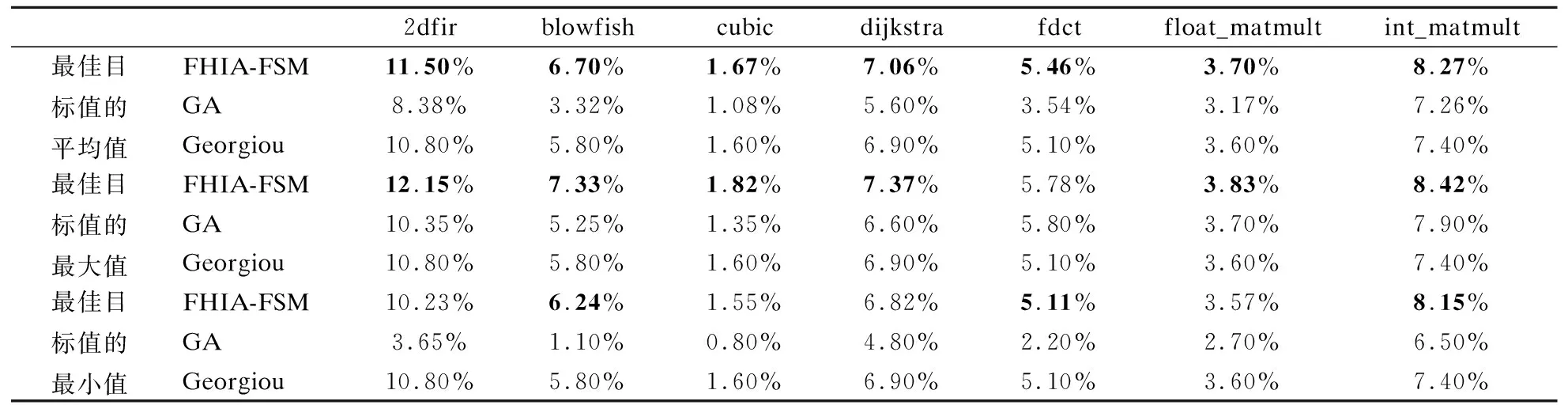
表5 在基准停机时间下本文FHIA-FSM、GA和Georgiou 3种算法针对各个案例所获取最佳目标值(相对于-O2等级的能耗改进百分比)的统计量结果Table 5 Statistical results of the best target value(the percentage of energy consumption improvement relative to -O2 level) obtained by FHIA-FSM,GA and Georgiou algorithms for each case under the baseline downtime

表6进一步给出了本文FHIA-FSM分别与GA和Georgiou针对基准停机时间下各案例最佳目标值(相对于-O2等级的能耗改进百分比)的秩和检验结果.表6中的第2列和第4列中的p-value值在全部7个案例下均远小于置信水平0.05,这从统计意义角度表明FHIA-FSM在基准停机时间下解质量显著优于GA和Georgiou.表6中第3列和第5列中effect size的值在所有7个案例下均大于0.8,这表明FHIA-FSM较GA和Georgiou能以较大概率上获得更优的解.图6所给出的统计盒图也直观地得到一致结论.

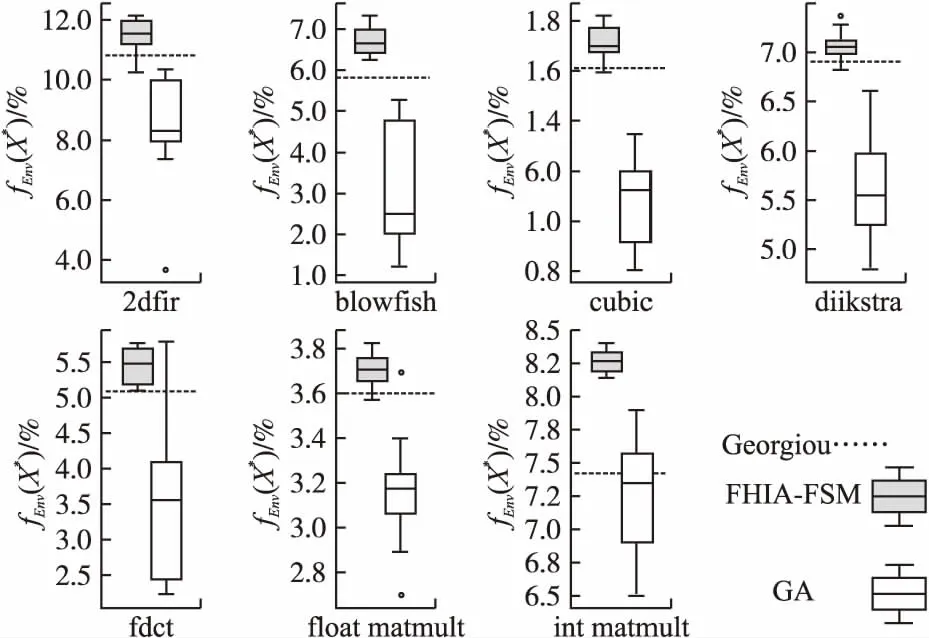
图6 在基准停机时间下FHIA-FSM、GA和Georgiou3种算法针对各案例所获取目标值fEnv(X*)(相对于-O2等级的能耗改进百分比)的统计盒图Fig.6 Boxplot of target value fEnv(X*)(the percentage of energy consumption improvement relative to -O2 level) obtained by FHIA-FSM,GA and Georgiou algorithms for each case under the baseline downtime

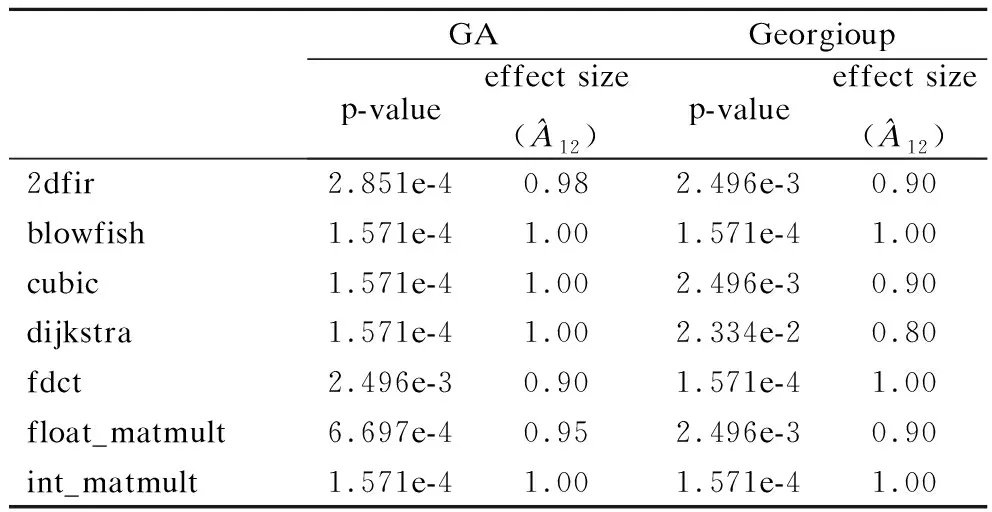
表6 本文FHIA-FSM分别与GA和Georgiou针对基准停机时间下各案例最佳目标值(相对于-O2等级的能耗改进百分比)的秩和检验结果Table 6 Rank-sum test results of the best target value(the percentage of energy consumption improvement relative to -O2 level)obtained by FHIA-FSM,GA and Georgiou for each case under the baseline downtime

为了进一步量化FHIA-FSM对解质量的改进情况,表7给出了FHIA-FSM较GA和Georgiou在基准停机时间下各案例解质量的平均相对改进百分比.从表7可以看出:各案例中FHIA-FSM较GA和Georgiou在解质量上均有较大提升,而且相对GA的提升更为显著.解质量的平均相对改进最好情况发生在blowfish案例中,FHIA-FSM较GA和Georgiou在解质量上分别提升了101.81%和15.52%.

表7 本文FHIA-FSM较GA和Georgiou在基准停机时间下各案例解质量(目标值)的平均相对改进百分比Table 7 Average relative improvement percentage of solution quality(target value)for each case under baseline downtime when HIA-FSM compares with GA and Georgiou

表5、表6、图6和表7的结果表明:不使用任何启发式信息的GA算法获取的解质量多劣于使用启发式信息进行寻优的算法FHIA-FSM和 Georgiou.这实证了启发式信息对于设计空间搜索这类LLVM选项序列优化方法提高解质量的重要性;此外,本文FHIA-FSM使用带能耗改进标注的频繁选项序列捕获选项交互的启发式信息较Georgiou使用标准等级隐含的选项依赖关系作为启发式信息对于提高解质量更为有效.因而,在基准停机时间下本文提出的FHIA-FSM较GA和Georgiou从统计意义上可获得更优的编译选项序列,使得各案例应用程序的运行能耗更低.

2)问题2(收敛速度):本文FHIA-FSM算法较Georgiou算法和GA算法能否以更少的计算时间达到基准解质量? 通过回答这一问题,可以进一步验证FHIA-FSM算法效率.亦即FHIA-FSM可否以更快的速度收敛得到基准质量的解.

为了避免测量噪声并进行归一化对比,在各案例中以Georgiou算法达到基准解质量时的优化用时作为基准时间T0,定义计算时间改进百分比IΔt%作为度量指标,如式(6)所示.式(6)中,T为FHIA-FSM或GA在达到基准解质量所花费的计算时间.

(6)

表8给出了本文FHIA-FSM、GA和Georgiou 3种算法针对各案例在达到基准解质量时计算时间改进百分比的统计量结果.表8中FHIA-FSM同时优于GA和Georgiou的值已被加粗表示.此外,在各案例中均以Georgiou的优化结果作基准停机时间和基准解质量,故表8中Georgiou的IΔt%指标值均为0.由表8的统计量结果可知:FHIA-FSM在7个案例下IΔt%的平均值和最大值均较GA和Georgiou更优;FHIA-FSM在7个案例下IΔt%的最小值也较GA更优.与此同时,GA在全部的7个案例下IΔt%的平均值和最小值均劣于Georgiou;除fdct、float_matmult和int_matmult案例外,其它4个案例IΔt%的最大值GA也都劣于Georgiou.

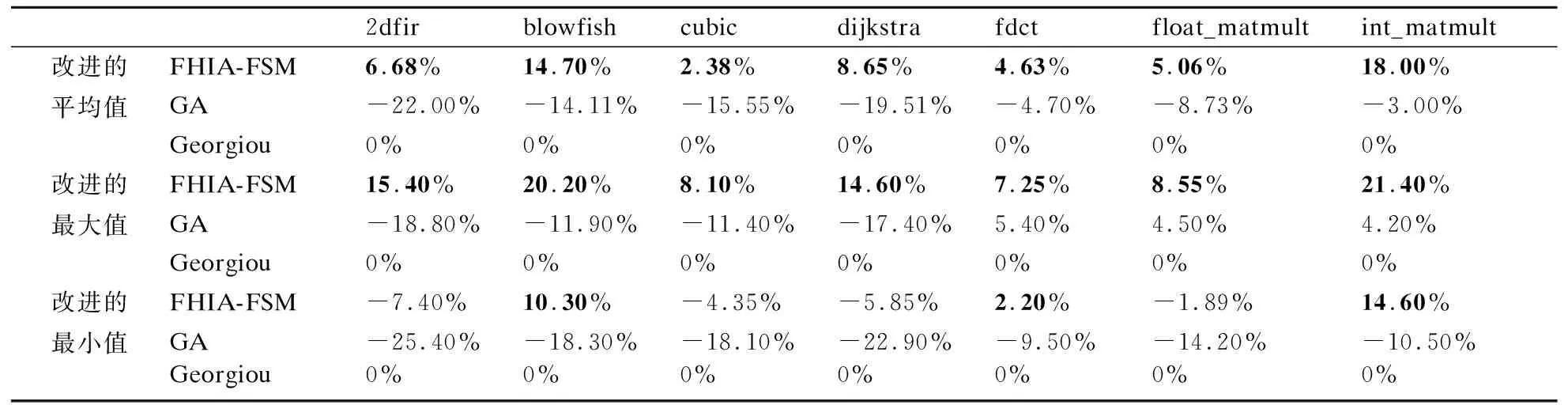
表8 本文FHIA-FSM、GA和Georgiou 3种算法针对各案例在达到基准解质量时计算时间改进百分比的统计量结果Table 8 Statistical results of the runtime improvement percentage obtained by FHIA-FSM, GA and Georgiou algorithms for each case under the baseline solution quality

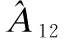
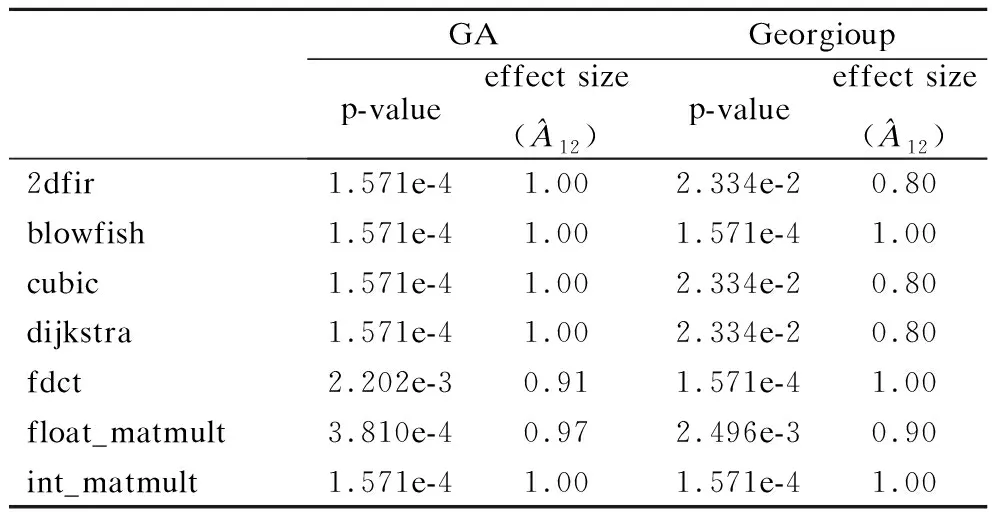
表9 本文FHIA-FSM分别与GA和Georgiou 针对各案例在达到基准解质量时计算时间改进百分比的秩和检验结果Table 9 Rank-sum test results of the runtime improvement percentage obtained by FHIA-FSM,GA and Georgiou for each case under the baseline solution quality

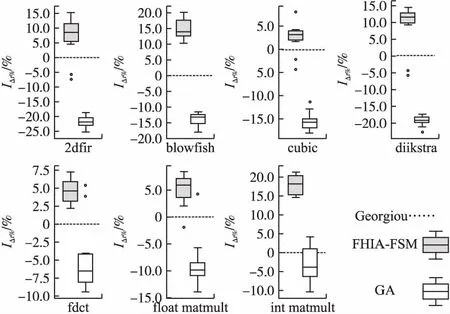
图7 FHIA-FSM、GA和Georgiou 3种算法针对各案例达到基准解质量下计算时间改进百分比IΔt%的统计盒图Fig.7 Boxplotof runtime improvement percentage IΔt% obtained by FHIA-FSM,GA and Georgiou algorithms for each case under the baseline solution quality

为了量化FHIA-FSM对收敛速度的改进情况,表10给出了FHIA-FSM较GA和Georgiou在各案例达到基准解质量时计算时间的平均相对改进百分比.从表10可以看出:各案例中FHIA-FSM较GA和Georgiou在收敛速度上均有较大提升,而且相对GA的提升更为显著.FHIA-FSM较GA和Georgiou在收敛速度的平均相对改进最好情况分别发生在blowfish和int_matmult案例中,其分别提升了25.25%和18%.

表10 本文FHIA-FSM较GA和Georgiou在各案例达到基准解质量时计算时间的相对改进百分比Table 10 Relative improvement percentage of runtime when HIA-FSM compares with GA and Georgiou under baseline solution quality for each case

表8、表9、图7和表10的结果表明:在达到基准解质量过程中,不使用任何启发式信息的GA算法较使用启发式信息进行寻优的算法FHIA-FSM和Georgiou需要消耗更多的计算时间.这说明启发式信息对于设计空间搜索这类LLVM选项序列优化方法不仅对于提高解质量,而且对于加快收敛速度也具有重要的作用;此外,本文FHIA-FSM使用带能耗改进标注的频繁选项序列捕获选项交互的启发式信息较Georgiou使用标准等级隐含的选项依赖关系作为启发式信息能更为有效地提高收敛速度.

7 总结和未来工作

文中提出一种频繁序列挖掘帮助的LLVM编译时能耗优化方法,以缓解现有设计空间搜索优化方法因求解过程中缺乏有效捕获和使用选项交互信息的手段而导致解质量不高和求解速度不快的问题.本文的具体贡献如下:

1)通过挖掘带能耗改进标注的频繁选项序列FOSE构建选项交互信息的挖掘模型并利用前缀树和后缀树进行表示,该挖掘模型及表示方法可用于获取任意多个选项之间交互信息;

2)针对迭代寻优过程设计了一种FOSE挖掘算法,FOSE挖掘算法可为新解生成提供有用、全面、可高效使用和时效好的选项交互信息;

3)提出了一种频繁选项序列挖掘帮助的LLVM编译时能耗迭代优化算法FHIA-FSM,FHIA-FSM算法设计了基于FOSE的前后缀树定义的新解生成机制,该新解生成机制可帮助提高新解生成质量,从而有助于提高算法收敛速度.

未来工作将面向LLVM选项复杂交互场景开展选项选择研究,以有效降低LLVM选项序列优化问题的解空间,达到进一步减少优化用时的目的.