一种组合优化模型驱动的微服务拆分方法

刘若宇,刘晓燕

(昆明理工大学 信息工程与自动化学院,昆明 650500)

1 引 言

随着移动互联网的发展,人们对软件的需求和访问量都在不断增加,由于传统的单体架构应用是将所有的功能模块集中在一起部署运行,因此其在软件扩展和维护时面临着很多难以解决的问题,为此越来越多的软件从业者选择用微服务架构这一新型的软件开发技术来替代原有的单体架构.

微服务是一种面向服务的分布式软件开发架构,它提倡将单一应用程序分解为若干松散耦合的微型服务,每个服务可以独立的部署运行,服务之间通过轻量级的通信机制相互协调调用[1],因此相比于单体架构,微服务架构在可扩展性和可维护性等方面有着天然的优势.然而在企业实践中,单体架构向微服务架构的迁移过程却存在着诸多问题,其中最大的一个问题是微服务的拆分太过依赖于工程师的主观经验,由此产生的拆分结果可靠性不高,耗时巨大,而且现下很多遗留的单体系统都存在着文档不全的问题,因此更加大了人工拆分的难度.

为了解决人工拆分所带来的各种问题,近年来国内外学者对此进行了大量的研究,提出了多种不同的微服务拆分方法,其主要可以归纳为以下4类:

1)基于静态代码分析:通过对目标程序源代码的静态结构进行分析,得到微服务拆分方案.例如Escobar等人[2]通过对代码的语法生成树以及语义标识符进行分析,再通过聚类操作完成微服务的拆分;Desai等人[3]使用程序的静态分析工具生成类之间的调用图,再通过图卷积神经网络得到微服务拆分方案.这类方法的不足之处是忽略了用户动态使用目标程序时的习惯偏好,程序的动态特征比如条件判断、多态等影响模块耦合的因素没有进行分析.

2)基于元数据分析:通过对系统开发阶段的各种文档比如UML图、接口文档、测试用例以及版本迭代历史等内容进行分析完成微服务拆分.例如Baresi等人[4]通过分析系统接口的语义相似度实现微服务的拆分;Mazlami等人[5]依据程序代码的修改历史提出了一种耦合策略进行微服务的拆分.这类方法要求系统具有完整的开发文档,对于一些存在文档丢失问题的遗留系统有一定的局限性.

3)基于工作流数据分析:通过分析程序动态运行时的数据流向得到微服务拆分方案.例如丁丹等人[6]以业务场景为依据,实现对数据库的划分,进而自底向上完成微服务的拆分;李杉杉等人[7]提出了一种高效的数据流信息自动化收集方案,并通过聚类算法实现了微服务的拆分.这类方法的缺点是可能存在代码覆盖率不够的问题,从而导致相关数据的获取出现偏差.

4)基于工作负载分析:通过对程序运行时的环境以及相关资源的消耗情况进行分析完成微服务拆分.例如Klock等人[8]提出了一种基于工作负载的特征聚类拆分微服务的方法;Abdullah等人[9]使用无监督的机器学习方法将具有相似性能的类划分进同一个微服务里.这类方法的缺点是只将系统工作负载的相似度作为拆分微服务的度量标准,而没有考虑到实际业务的相关性.

针对已有研究中的一些不足,本文提出了一种组合优化模型驱动的微服务拆分方法,该方法将微服务拆分问题建模为一种组合优化问题,通过对程序进行静态分析和动态执行分别得到类之间的耦合度以及业务相关度,然后依据微服务的高内聚低耦合原则和业务一致性原则提出需要优化的目标函数,最后使用改进后的人工鱼群算法找到使目标函数取最优值时的微服务拆分方案.实验表明该方法能有效改善已有研究中单一分析方法所带来的不足,具有更好的拆分效果.

2 微服务拆分的组合优化模型

2.1 组合优化问题

组合优化问题是最优化问题的一种,其目的是从一组离散的对象集合中找到“最优”的一个对象,而“最优”的评估标准往往是依据该对象集合所对应的一个目标函数,使得该目标函数取得最大值或最小值的对象就是要找的“最优”对象,即该组合优化问题的最优解.通常可描述为:令Ω={s1,s2,…,sn}为所有离散的对象构成的解空间,F(si)为对象si对应的目标函数值,要求寻找最优解s*,使得对于所有的si∈Ω,有F(s*)=maxF(si).

2.2 构建模型

在微服务的拆分过程中,假设原有的单体架构应用存在k个类,最终拆分后的微服务数量为s,为了将微服务的拆分问题建模为组合优化问题,本文将微服务的拆分模拟成一种随机的过程,则k个类会被随机分配进s个微服务里,最终的拆分结果可以表示为M={m1,m2,…,ms},其中m1,m2,…,ms分别为每一个拆分后的微服务.基于以上分析,k个类就会产生n种不同的拆分结果Φ={M1,M2,…Mn},其中n是第2类Stirling数[10],表示将k个不同的元素拆分成s个集合的方案数,则Φ就是所要构建的组合优化模型中的解空间.

为了找出解空间中的最优解,即最佳的微服务拆分结果,还需要构建一个目标函数,并且该目标函数能够真实地反映出微服务拆分结果的优劣.根据学术研究和企业实践的相关经验,一个好的微服务设计通常都符合以下两个原则[1]:

1)高内聚低耦合原则:同一个微服务内部类的耦合度高于不同微服务之间类的耦合度.

2)业务一致性原则:同一个微服务内部类的业务相关度高于不同微服务之间类的业务相关度.

因此,本文对目标函数的构建主要由两部分组成,其中第1部分基于对源程序的静态分析,提出了一种计算类的耦合度的方法,用以评估微服务拆分结果是否符合高内聚低耦合原则;第2部分基于对系统的动态执行,提出了一种计算类的业务相关度的方法,用以评估微服务拆分结果是否符合业务一致性原则,最后将这两部分相结合得到最终的目标函数.

2.2.1 类的耦合度

根据代码的静态语义和语法分析,类与类之间的耦合关系大致可以分为以下3类:

1)继承关系:子类a继承父类b的全部功能,并可以增加新的功能.在代码语法中通常用extends等关键字来表示.继承关系是一种强耦合关系,如果父类的功能发生变化,必然会影响子类的功能.

2)关联关系:类a包含了类b的一个实例.在代码语法中通常表现为类b作为类a的一个属性存在.关联关系是一种固定的、长期的关系,但因为其涉及的两个类是一种并列关系,因此其所表示的耦合关系要弱于继承关系.

3)依赖关系:类a负责构造类b的一个实例,或使用了类b的一个服务.在代码语法中通常表现为类b作为类a方法中的一个参数、变量或返回值存在.依赖关系是一种临时的、偶然的关系,其所表示的耦合关系要弱于关联关系.

用静态代码分析工具检查源程序中的类之间是否存在上述3种耦合关系,生成图1所示的类耦合关系图,再对这3种关系分别赋予不同的权值,得到两个类的耦合度计算公式如式(1)所示:

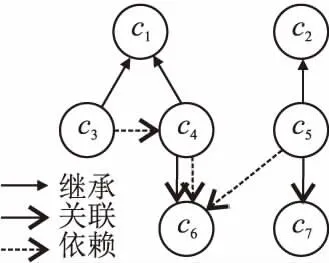
图1 类耦合关系图Fig.1 Class coupling diagram

C=α1·Gen+α2·Ass+
α3·Dep

(1)

其中,C表示类a对类b的耦合度,其值越大则类a对类b的耦合度越高.Gen、Ass、Dep分别表示类a对类b是否存在继承、关联、依赖关系,若存在则其值为1,否则为0,特别要注意的是,这里类a与类b的耦合关系是一种单向关系,而非双向.相关的权值为α1=0.6,α2=0.3,α3=0.1.

根据式(1)依次求出源程序中每两个类之间的耦合度并将其用一个k×k的矩阵C表示,其中C[a][b]=C,k为源程序中类的数量.则拆分后的微服务的耦合度可以表示为式(2)所示:

(2)

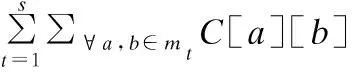
2.2.2 类的业务相关度

在一个应用系统的执行过程中,若两个类共同完成某一项业务功能的频率越高,则表示这两个类的业务相关度越大.为此,本文通过测试用例对系统进行动态执行,然后监控出类与业务功能之间的对应关系.

1)测试用例

测试用例的选取往往要求相关人员对应用系统的业务功能非常熟悉,而且人为的选择会存在一定的主观性和不确定性,为了避免这些人为因素的影响,本文选择使用系统中所有的用户接口作为测试用例.用户接口是用户与系统进行直接交互的最小单元,它覆盖了用户可以使用的所有业务功能,同时用户接口的获取可以直接通过工具自动地完成,而不用依赖说明文档或是人的主观经验,这样既可以提高效率、减小人为因素带来的不确定性,同时也提高了测试用例的业务覆盖度.

2)类与业务功能的关系图

通过程序动态监测工具追踪系统对测试用例的执行过程,分析执行某一业务功能时使用到的类的情况,得到图2所示的类与业务功能的关系图,其中每一个业务功能对应一个或多个类,每一个类同时对应一个或多个业务功能.

图2 类与业务功能的关系图Fig.2 Diagram of classes and business functions

3)业务相关度

定义Uc为类c对应的业务功能的集合,|Uc|为该集合中业务功能的数量,则任意两个类a和b的业务相关度B(a,b)等于a、b共同完成某一业务功能的数量与它们完成的所有业务功能数量之比,如式(3)所示:

(3)

根据式(3)依次求出系统中每两个类的业务相关度并将其用一个k×k的矩阵B表示,其中B[a][b]=B(a,b),k为类的数量.则拆分后的微服务的业务相关度可以表示为式(4)所示:

(4)

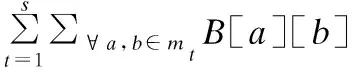
2.2.3 目标函数

得到微服务的耦合度CM和业务相关度BM后,要构建的组合优化模型的目标函数就等于这两者之和,如式(5)所示:

f(M)=CM+BM

(5)

其中CM和BM分别用来衡量该微服务拆分结果M的高内聚低耦合性和业务一致性,f(M)越大,则M越符合微服务设计的高内聚低耦合原则和业务一致性原则,因此其表示的微服务拆分效果越好.

生成最终的目标函数之后,微服务拆分问题的组合优化模型就可以描述为:

在微服务拆分的所有可行解空间Φ={M1,M2,…Mn}中寻找最优解M*使得对于所有的Mi∈Φ有f(M*)=maxf(Mi),则M*就是微服务拆分的最优结果.

3 人工鱼群算法的应用

求解组合优化问题的算法有很多种,经过分析比较发现,相比于其他算法,人工鱼群算法中的人工鱼模型更易于表示出微服务拆分的结果,并且由于其对初值不敏感的特性,使得在初始时随机生成微服务拆分结果对算法性能不会产生影响,最后该算法具有更好的寻优速度及全局寻优能力,因此本文选择了人工鱼群算法用于求出文章第2节所提出的目标函数的最优解,进而得到最佳的微服务拆分方案.

3.1 人工鱼群算法简介

人工鱼群算法AFSA(Artificial Fish School Algorithm)是李晓磊等人通过对自然界中鱼群行为的研究从而提出来的一种群体智能优化算法[11].该算法的核心思想是通过构造人工鱼并利用鱼的觅食行为、聚群行为、追尾行为这3种行为驱动人工鱼游向食物浓度最高的地方,从而实现具体问题的寻优.由于该算法具有收敛速度快、对具体目标函数要求不高等优点,从而被广泛地应用于各种组合优化问题上.以下是对AFSA中3种行为的具体描述:

1)觅食行为:设人工鱼当前状态为Xi,其在视野范围内随机选择一个状态Xj,如式(6)所示:

Xj=Xi+Visual×Rand()

(6)

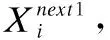
(7)

其中Step是人工鱼的最大步长.若Yj≤Yi,则反复迭代至最大觅食次数,如果仍未满足移动条件,则随机游向一个状态.

(8)

否则进行觅食行为.

(9)

否则进行觅食行为.

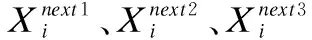
3.2 微服务拆分的AFSA模型

3.2.1 人工鱼模型

1)人工鱼的表示

在微服务拆分的AFSA模型中,人工鱼的状态定义为微服务拆分的所有可行解空间Φ={M1,M2,…Mn}中的一个解Mi,它代表了一个可能的拆分结果,用一个集合表示为式(10)所示:

Mi={m1,m2,…,ms}

(10)

集合中元素的数量s为要拆分的微服务的数量,由行业专家确定.每个元素mi代表了一个微服务,其由系统中的若干个类组成,可以表示为式(11)所示:

mi={c1,c2,…,ck}

(11)

其中ci是系统中的一个类,k为该微服务所包含的类的数量.

2)人工鱼的距离

在微服务拆分的AFSA模型中,两个微服务m1和m2的距离d(m1,m2)定义为将m1转换为m2所要增加和删除的类的数量,其等于不同时属于m1和m2的类的数量,如图3中阴影部分所示.具体的计算公式如式(12)所示:

图3 微服务的距离示意图Fig.3 Diagram of distance between microservices

d(m1,m2)=|m1∪m2|-|m1∩m2|

(12)

在微服务拆分的AFSA模型中,两条人工鱼M1和M2之间的距离D(M1,M2)定义为将M1转换为M2最少需要移动的类的数量.如图4所示,设M1={{c1,c2,c4},{c3,c5}},M2={{c1,c2,c3},{c4,c5}},则将M1转换为M2,最少需要移动c3和c4两个类,因此D(M1,M2)=2.

图4 人工鱼的距离示意图Fig.4 Diagram of distance between artificial fishes

在M1和M2中的微服务之间存在一种一对一的对应关系(mi,mj),其中mi∈M1,mj∈M2,使得所有mi和mj之间的距离总和最小,则D(M1,M2)等于这个最小值的一半,如式(13)所示:

(13)

例如图4中,

D(M1,M2)

本文使用贪心算法求解这种对应关系,具体步骤如算法1所示.

算法1.求解微服务对应关系的算法

1.FormiinM1:

2. FormjinM2:

3. Ifd(mi,mj) is min:

4. (mi,mj) is true;

5.M2removemj;

遍历M1中的每个微服务mi,用贪心策略寻找M2中与之距离最短的微服务mj,则mi和mj存在对应关系(mi,mj).

3.2.2 人工鱼行为模型

在微服务拆分的AFSA模型中,食物浓度定义为目标函数f(M)=CM+BM,食物浓度最高的地方对应的Mmax即为最优的微服务拆分结果,人工鱼通过3种行为不断游向食物浓度最高的地方,具体行为模型如下:

1)觅食行为

在微服务拆分的AFSA模型中,觅食行为表示人工鱼在可行解空间中随机地寻找最优的微服务拆分结果.

设人工鱼当前状态为Mi,其在视野范围内随机选择一个状态Mj,其值等于Mi随机移动Rand(Visual)个类到其它微服务得到的拆分结果,其中Visual是人工鱼的最大视野,根据系统中类的数量人为设定,Rand(x)产生一个0到x之间的随机整数.

若f(Mj)≤f(Mi),则反复迭代至最大觅食次数,如果仍未满足移动条件,则随机游向一个状态.

2)聚群行为

在微服务拆分的AFSA模型中,聚群行为表示人工鱼寻找邻近伙伴所表示的微服务拆分结果的共同特征,并游向满足该特征的状态.

定义人工鱼Mi所对应的关系矩阵Rk×k如式(14)所示:

(14)

其中k是系统中类的数量,a和b是系统中任意两个类.

设人工鱼当前状态为Mi,视野范围内的伙伴数目为nf,伙伴的中心状态为Mc,则Mc对应的关系矩阵如式(15)所示:

(15)

其中round()是对矩阵中的每个元素进行四舍五入取整操作.Rc代表了邻近伙伴所表示的微服务拆分结果中类之间关系的共同特征,但有时候得到的Rc会存在一些类关系的冲突,比如Rc[a][b]=1,Rc[a][c]=1,但Rc[b][c]=0,即表示a和b,a和c都属于同一个微服务,但b和c却不属于同一个微服务,这时候需要先对Rc进行去冲突的操作,然后再将其转换为对应的Mc,具体的步骤如下所示:

Step1.遍历矩阵Rc,如果Rc[a][b]=1且Rc[a][c]=1,但Rc[b][c]=0,则令Rc[a][c]=0,Rc[c][a]=0.

Step2.将Rc转换为对应的微服务拆分结果Mc.

Step3.若Mc对应的微服务数量小于预先设定的微服务数量s,则每次将类数量最多的微服务随机拆分为两个,直至微服务数量等于s.

Step4.若Mc对应的微服务数量大于s,则每次将类数量最少的两个微服务合并为一个,直至微服务数量等于s.

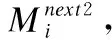
3)追尾行为

在微服务拆分的AFSA模型中,追尾行为表示人工鱼游向邻近伙伴中最优的一个微服务拆分结果的状态.

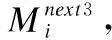
3.2.3 整体流程

AFSA求解微服务拆分问题的整体流程如下:

Step1.设定鱼群数量n,视野Visual,步长Step以及迭代次数tryNumber等参数.

Step2.设定要拆分的微服务数量s,根据s以及系统中类的数量随机初始化n个微服务拆分结果,作为初始人工鱼的状态{M1,M2,…,Mn}.

Step3.构造目标函数f(M)=CM+BM作为食物浓度.

Step4.对每条人工鱼分别执行觅食行为、聚群行为和追尾行为,得到相应的状态以及食物浓度(Mnext1,f(Mnext1))、(Mnext2,f(Mnext2))、(Mnext3,f(Mnext3)).

Step5.令f(Mnext)=max(f(Mnext1),f(Mnext2),f(Mnext3)),其对应的Mnext作为这条人工鱼下一次游动的状态,对鱼群中所有人工鱼执行相同的操作.

Step6.反复执行Step4和Step5,直到达到迭代次数tryNumber.

Step7.输出人工鱼聚集最多的状态M,即为最优的微服务拆分结果.

4 实验设计及结果分析

为了验证提出的微服务拆分方法的可靠性,本文选择了4个开源项目进行实验,如表1所示,它们都是基于单体架构的项目,并且被广泛应用于相关的学术研究中.

表1 项目信息Table 1 Project information

本文首先以其中一个系统JpetStore为例描述了完整的实验流程并展示了具体的微服务拆分结果,然后通过相关的评价指标对所有项目的拆分结果进行了评估,最后与其他的拆分方法进行比较分析,说明了本方法的优越性.

4.1 案例分析

JpetStore是一个基于单体架构的小型宠物电商系统,对其进行微服务拆分的实验流程如下:

1)使用工具java-callgraph(https://github.com/gousiosg/java-callgraph)对系统源程序中所有类之间的继承关系、关联关系、依赖关系进行分析,根据式(1)计算出类之间的耦合度,并将其保存在一个矩阵中.

2)提取出源程序中的20个用户接口作为测试用例,其涉及注册、登录、查询个人信息、修改个人信息、搜索商品、浏览商品、添加购物车、移除购物车、下订单、查看订单等十多种业务功能.

注释:画框部分表示与人工拆分结果不一致的类.

3)基于Aspectj框架(http://www.eclipse.org/aspectj)对测试用例进行执行追踪,得到类与业务功能的关联关系,根据式(3)计算出类之间的业务相关度,并将其保存在一个矩阵中.

4)根据1)和3)的生成结果构造出目标函数.

5)设定微服务的拆分数量为4,AFSA中的人工鱼数量为10,运行AFSA经过30次迭代后目标函数收敛于最大值,得到最优的微服务拆分结果如表2所示.

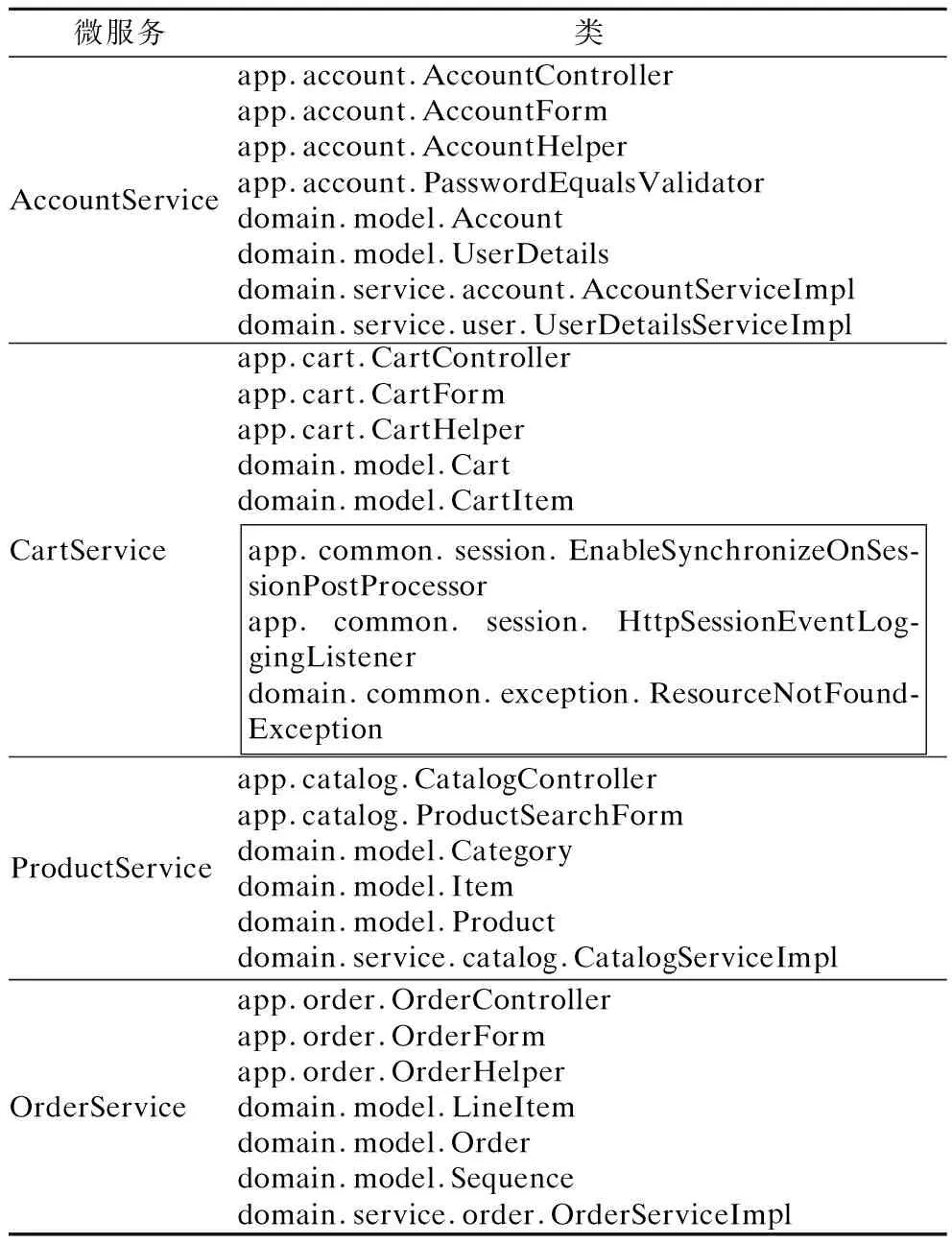
表2 微服务拆分结果Table 2 Result of microservice decomposing

该系统最终被拆分为4个微服务:AccountService、CartService、ProductService、OrderService,分别实现账户、购物车、商品和订单功能.将其与人工拆分的结果对比后发现几乎所有类的划分都保持一致,除了CartService中画框部分所示的3个类的划分略有不同,人工拆分的结果将这3个类划分进了商品相关的微服务中.经分析后发现这3个类都是和全局会话以及异常相关的处理类,并不涉及业务逻辑相关的工作,因此人工拆分将其划分进了可能使用频率比较高的商品相关的微服务中,而本方法则是根据耦合度和业务相关度进行量化分析,将其拆分进购物车相关的微服务中,实际上并不影响整体微服务架构的构建.

4.2 评估指标

为了验证应用本方法所得到的结果与实际微服务拆分结果的匹配度,本文将人工拆分的结果作为标注,得到微服务的拆分准确率ACC计算公式如式(16)所示:

(16)

其中|ca|表示和人工拆分结果相一致的类的数量,|csum|表示系统中类的总数量,ACC越大,表示拆分准确率越高,拆分的结果越符合预期.

由于人工的拆分结果难免会存在一定的主观性和片面性,因此还需要一些指标对微服务拆分结果的质量进行更为客观的评估,参考相关研究中的评估方法,本文选取了3种指标,具体如下:

1)inter-partition call percentage (ICP)[12]:用来度量发生在两个微服务之间的运行时调用的百分比,因此ICP越小,微服务拆分的结果越好.其计算公式如式(17)所示:

(17)

其中ci,j表示两个微服务相互调用的次数.

2)business context purity (BCP)[12]:用来度量每个微服务业务用例的平均熵.微服务的用例由与其成员类相关联的所有用例标签组成.如果一个微服务实现了一小组用例,那么它就被认为是功能内聚的.BCP越小,微服务的拆分效果越好.其计算公式如式(18)所示:

(18)

其中|BCi|表示微服务i的测试用例数量.

3)structural modularity (SM)[13]:从结构的角度度量微服务的模块化质量,SM越大,微服务的拆分效果越好.其计算公式如式(19)所示:

(19)

其中scohi用来度量微服务的内聚性,ui表示微服务内部交互的次数;scopi,j用来度量微服务的耦合性,σi,j表示微服务之间交互的次数.

4.3 对比试验

为了使最终的评估结果更具说服力,本文从文章第1节所归纳出的4类主流的微服务拆分方法中各选择了一种具有代表性的方法用于对比实验,具体如下:

1)CoGCN[3]:通过类的静态调用图以及图卷积神经网络完成微服务的拆分.

2)MEM[5]:通过逻辑和语义关联计算耦合,并使用最小生成树的方法得到微服务的拆分结果.

3)SdBu[6]:以业务场景作为测试用例完成数据库的拆分,再自底向上完成微服务的拆分.

4)ULA[9]:使用程序运行时的性能作为拆分依据,将具有相似性能的类划分进同一微服务内.

4.4 实验结果

在实验项目和微服务数量预设值相同的条件下完成所有的对比实验,得到的评估指标结果如表3所示.

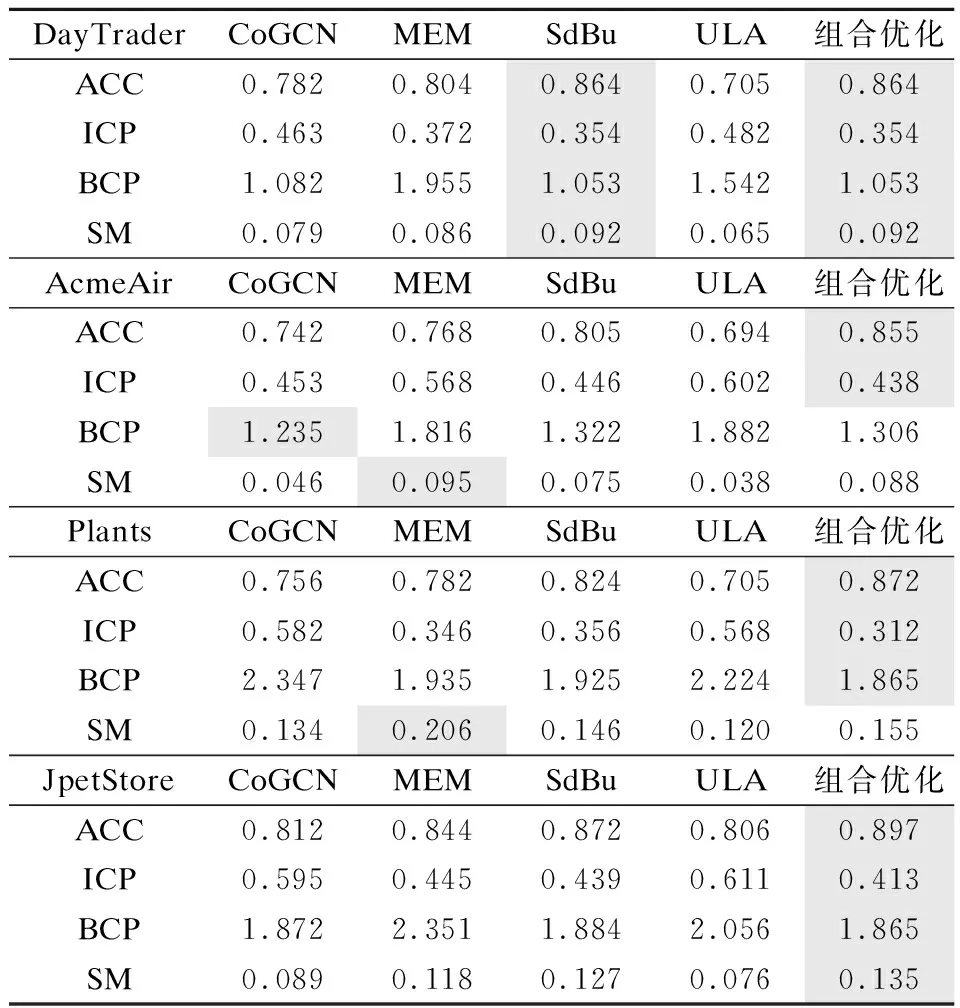
表3 评估指标结果Table 3 Results of evaluation indicators

通过对表3的分析可以发现本文提出的方法ACC指标和ICP指标在4个系统中都是最优的,BCP指标在3个系统中是最优的,SM指标在2个系统中最优,2个系统中排名第二.因此本文提出的方法总体优于其他方法,这是因为:

1)本文使用的方法符合行业内人工拆分微服务的准则和习惯.

2)本文使用类之间的继承、关联、依赖关系作为类的耦合标准,将耦合度高的类划分进同一个微服务,从而减少了微服务之间的调用次数.

3)本文使用类与业务功能的关联关系作为业务相关度的标准,将实现相同功能的类划分进同一个微服务,从而使得每个微服务的业务独立性更高.

4)本文根据微服务的高内聚低耦合原则和业务一致性原则构建组合优化模型的目标函数,所以得到的微服务模块化质量更高.

5 结束语

本文提出一种组合优化模型驱动的微服务拆分方法,该方法将具体的微服务拆分问题建模成为抽象的组合优化问题,根据微服务的高内聚低耦合原则以及企业实践中的业务一致性原则,通过类之间的耦合度以及业务相关度生成了组合优化的目标函数,最后通过人工鱼群算法得到最优的微服务拆分方案.实验结果表明,该方法能有效提高拆分后微服务的模块化质量以及业务独立性,降低了行业内单体系统向微服务系统迁移的成本.未来的工作将着眼于改进人工鱼群算法在该组合优化模型中的时间复杂度,以提高微服务拆分的效率.