融合位置动力学的物理建模优化方法研究
罗 丹,张 禹,李 佳
(沈阳工业大学 机械工程学院,沈阳 110870)
1 引 言
虚拟手术就是依托虚拟现实技术和信息技术,在计算机中建立一个虚拟环境[1],依靠医学影像数据和虚拟环境信息,可以进行医学培训、手术模拟、术中引导、术后康复和远程医疗.虚拟手术融合了计算机技术、生物学、现代医学、机器人学等多学科领域,主要由医学数据处理、人体组织器官(主要是软组织)建模、形变及切割仿真、力反馈4部分构成,为用户提供了视觉和触觉的交互感知[2].软组织的物理建模是虚拟手术研究的重点,物理模型是指人体软组织模型在与手术器械交互过程能够表现出来的视觉和触觉信息(包括形变位移和力反馈).它首先通过对医学图像的处理与分割获得人体生物组织的几何模型,然后利用对人体组织生物力学特性的研究,根据软组织在受力的情况下,产生的形变过程和计算的反馈力来进行物理建模[3].合理地建立虚拟手术仿真模型,既能体现真实性和沉浸感,又能保证虚拟仿真的实时性.
由于人体软组织具有不均匀性、各向异性、非线性和粘弹性等性质[4,5],其形变过程中对于力与形变的关系也表现出相应的复杂性.因此,为了保证形变模型的准确性,更好的将可视化与触觉反馈结合,在虚拟手术中软组织的物理建模中必须考虑这些生物力学特性.目前,描述软组织变形的物理模型中最简单的是根据胡克定理的线弹性模型(linear elastic model),但这个模型一般只适用于位置移动较小的情况,并且线性模型不足以表达复杂的运动情况,常用非线性模型来进行表述:例如线弹性模型、粘弹性模型、简单的Newton 粘性流公式等[6,7].大多数的人体组织材料既有弹性又有粘性,因此模型的建立必须基于生物力学特性的基础上,兼顾实时性.在真实性和实时性之间折衷来模拟软组织形变.
软组织物理建模技术即软体的变形模拟技术,国内外学者做了大量的研究.基于物理的方法中最常用的是质点弹簧法(Mass Spring Method,MSM).Terzopoulos最早了提出质点弹簧模型,对皮肤的形变过程进行了仿真[8].质点弹簧法是将连续的组织离散化为一系列有质量的点,质点之间通过弹簧来进行连接.质点受到外力、弹力、阻尼力的作用,通过牛顿第二定律来计算其变形[9,10].Waters K.等人使用质点弹簧法对人脸进行了仿真[11].国内鲍春波等人在2006年对质点弹簧法进行改进[12],按照质点受力大小进行动态细分,实现了仿真精度的提高.这种方法是根据牛顿第二定律计算出加速度的内部和外部力,然后根据时间积分方法来更新速度,最后更新对象的位置.MSM结构简单,计算成本低,因此在软组织建模中应用广泛,但在形变量较大时振荡效果明显,容易产生塌陷等变形缺陷,不易表现真实的形变特性.
基于物理的质点弹簧方法(Mass Spring Method,MSM),在呈现出时域相关的非线性及粘弹性的力学特征下,有着局部变形大且失真的弱点;而基于几何的PBD模型很适合应用到以实时性和手术操作为主要目标的虚拟手术模拟器中,虽然可以采用不同的约束函数来模拟变形特征,且鲁棒性好,却很难表现出时域特性;XPBD对不同材质的影响不明显,精度表现一般.根据MSM和PBD都是通过空间离散质点的运动位置来模拟形变特征的共通点,本文提出了一种将MSM与PBD相结合的模型,即融合生物力学特性的位置动力学模型(Bio-based PBD,B-PBD).两种模型的整合思路也来源于XPBD的推导过程:将非线性、粘弹性被引入到弹力计算中,由牛顿第二定律根据弹力及约束力的合力计算出质点位置.模型分为两个部分:粘弹性模型反应软组织的生物力学特性;PBD处理复杂的效果,如不可压缩性,并保持模型的稳定性.实现了快速,稳定的模拟及复杂变形的仿真.
2 融合生物特性的位置动力学建模(Bio-based PBD,B-PBD)
2.1 模型建立
本文的物理模型采用四面体网格,基于位置的动力学算法用到两个基本条件:即四面体的顶点和约束.假设四面体网格中顶点数为N,四面体每一个顶点的信息包括:质量mi、位置Pi、速度Vi,模型中约束条件数目为M,第j个约束条件的基数为nj,每个约束可以表示成Cj(xi1,…xinj)=0,则j满足类型相等的约束.
PBD的核心分为两步:
1)通过外力的显式步进求到一个暂时的形变位置;
2)定义一系列的约束.通过应用一系列的约束来模拟不同的形变效果,来改变这个暂时的形变位置得到最终的形变位置.
PBD单元模型2在顶点xi之间设置拉伸约束、在两个三角面片之间设置弯曲约束、两个四面体之间设置体积约束.四面体顶点的位置改变时,约束函数将每个点投影到合适的位置,实现了由位置计算变形.B-PBD单元模型如图1(a)所示.在原有PBD约束的基础上,在顶点xi之间增加了三参量质点弹簧模型约束,表达模型的生物力学特性.三参量模型如图1(b)所示.在其顶点处布置具有质量、位置、半径、转动惯量等属性的填充球体,填充球之间采用三参量粘弹性结构进行连接.当软组织器官表面受到力的作用后,受力的填充球会通过四面体的边带动与之相连的填充球运动,模拟软组织变形.在模型外覆盖面模型,通过添加纹理使模型更加逼真,满足视觉要求.
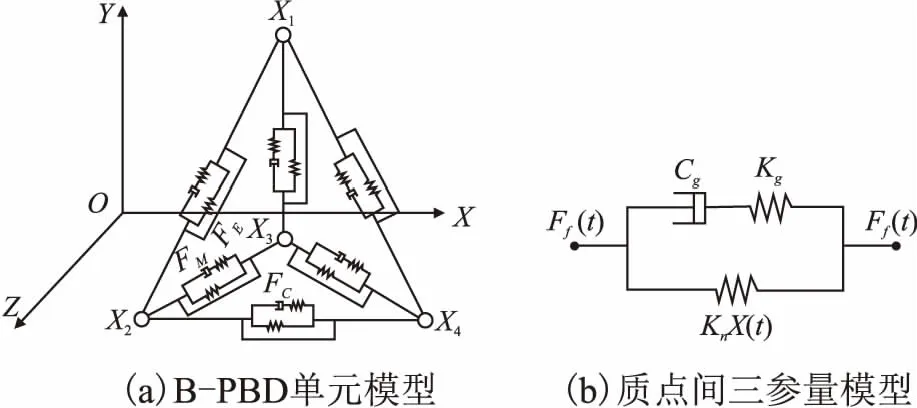
图1 B-PBD模型Fig.1 Model of B-PBD
2.2 约束投影
位置动力学使用约束条件来控制物体的变形,这些约束条件一般基于几何规则,根据几何规定定义的约束函数[16].约束函数用于确定动态物体的力学特性.约束投影即讲修正质点运动来满足约束函数的过程.
计算过程如下:
1)对四面体每个顶点的位置Pi和速度Vi进行初始化;

(1)
式中:F为外力;ωi=1/mi,mi为顶点质量;Damp(*)为阻尼函数.
根据外力预测下一时间间隔内顶点的位置:
(2)
(3)
(4)
5)循环计算,返回第2)步,更新每个顶点的速度,预测下一时刻的位置.对于每个顶点的位置改变量ΔP:
(5)
式中,C(P1,P2,…,Pn)为顶点位置的约束函数;▽PiC(P1,P2,…,Pn)为函数关于顶点Pi的梯度.
在模拟软组织变形中,常用的约束有拉伸约束、弯曲约束、体积约束、能量保持约束等.拉伸约束是指当两个填充球在外力的作用下距离发生变化时,拉伸约束使其回到初始位置.对于拉伸约束可得:
C(P1,P2)=|P1-P2|-d
(6)
其中,P1和P2为两个顶点,d是两个顶点之间的静止距离,对P1和P2分别求梯度,并代入到公式(5)中,可得:
(7)
(8)
体积保持约束用于防止出现“空心”的效果,在外力的作用下四面体的体积不发生变化.体积约束的函数表达式为:

(9)
其中,V0是四面体的体积,P1,P2,P3,P4是四面体的4个顶点,对4个顶点求梯度,并代入公式(5)中,得到:
(10)
2.3 算法推导
模型对象由一组质点,约束和弹簧、阻尼组成.质点的位置由其总力负荷控制.计算的目标是找出每个步骤中每个质点的实际位置.基于牛顿第二定律:
(11)
其中x=[x1x2…xn]T是质点位置的列向量,是质点的加速度.M为质量的对角矩阵,FC、FM和FE分别是势能约束力、弹簧和外力的列向量.
约束能量势被定义为:
FC=-▽UT(x)
(12)
其中U(x)为能量势能.
将方程(11)离散化,上标n表示时间步长指数,则有:
(13)
(14)
其中C(x)=[C1C2…Cm]T为列的约束函数,α是对角柔度矩阵,相当于对应的约束逆刚度矩阵.则来自弹性势能的力由U的负梯度:
FC=-▽xUT=-CTα-1C
(15)

(16)
可得:
(17)

(18)
(19)
将方程(18)、(19)分别表示为g和h,则有:
g(x,λ)=0
(20)
h(x,λ)=0
(21)
线性化方程可得:
(22)
其中K=∂g/∂x.可以针对Δx和Δλ求解该系统,并相应地更新乘子和位置:
λi+1=λi+Δλ
(23)
xi+1=xi+Δx
(24)

(25)
得到位置更新:
Δx=M-1▽C(xi)TΔλ
(26)
拉格朗日乘子的修正量:
(27)
在约束求解期间,首先计算单个约束的Δλ,然后使用等式(23)、式(24)更新系数和乘子.
软组织的粘弹性通过三参量质点弹簧(MSM)模型来体现.该模型的弹性特性通过弹簧结构来表示,粘性特性通过弹簧和阻尼串联结构来表示,如图1(b)所示.软组织的形变量即为系统叠加的位移总和.
由图1(b)可知:
Fn(t)=KnXn(t)
(28)
(29)
Ff(t)=Fg(t)+Fn(t)
(30)
式中,Kn,Kg是弹簧弹性系数,Cg是粘性系数,Fn(t)、Fg(t)、Ff(t)分别是外力,Xn(t)、Xg1(t)、Xg2(t)是由外力引起的位移.
经过三维重建后的面模型,使用Tetgen算法对四面体网格进行划分.以正四面体为例,如图2所示.在正四面体OABC中,O,A,B,C分别代表每个填充球体的球心,在力F(t)的作用下,若只考虑拉伸力,忽略弯曲和扭转的条件下,则球心O移动到了O′点,OB粘弹性结构长度发生了变化,与之相连接的OA,OC长度也相应发生改变.由于变形量非常小,忽略球心A,B,C球的移动量.设形变前后OB长度变化量OO′为X(t),CO′与O′B夹角为θ(60°≤θ≤90°),OC长度设为y,形变后O′C长度为x,则变化值ΔX(t)=y-x.

图2 小变形受力分析Fig.2 Stress analysis of small deformation
根据几何关系得出:
(31)
(32)
由胡克定律得出:
Fk(t)=2K′ΔX(t)cosθ
(33)
令λ满足:
(34)
则公式(33)可以写成:
F(t)=FK(t)+Ff(t)
(35)
其中,K′是三参量粘弹结构的弹性系数,Fk(t)是三参量模型受力分量.
根据小变形理论,则有:
F(t)=FK(t)+Ff(t)
(36)
根据上述的小变形理论受力方程(35)及(36),建立混合填充球模型的力位移方程,拉氏变换可得:
(37)
其中τ是松弛时间,满足:
(38)
1)力-时间方程建立

(39)
当t→0+时,
F(0+)=(λ+Kn+Kg)X0
(40)
当t→∞时,
F(∞)=(λ+Kn)X0
(41)
2)位移-时间方程建立
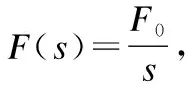
(42)
其中:
(43)
当t→0+时:
(44)
当t→∞时:
(45)
每个质点的弹簧力:
FM=Fd+F
(46)
其中:
(47)
b0和b1为两个阻尼约束[17],Fd为直接作用在速度上的阻尼,F为三参量模型的总弹性力.
2.4 算法流程
根据上面的推导,可以总结出算法的流程如表1所示.

表1 算法流程Table 1 Algorithm flow of B-PBD
基于生物力学特性的位置动力学方法的概念是将行为模型分成两个部分:用XPBD以适应拓扑修改和基础组织的材料非均质性,处理复杂的效果,并保持模型的稳定性,变形效果取决于迭代器计数;三参量MSM模型反映软组织的物理特性,非线性和粘弹性,并将扩展弹簧力作为外力引入以估算质点位置,保持了最终质点位置的稳定性.
与PBD和XPBD相比,B-PBD在预测位置步骤中加入了反应软组织生物力学特性的改进的三参量模型.首先在弹簧弹力计算过程中体现了非线性与粘弹性,基于牛顿第二定律,在进行下一时刻位置预测时,将弹簧力作为外力,采用显式欧拉法求解.基于PBD的体积不变约束对质点位置进行修正.在约束投影步骤中,按照预先给定的约束的顺序分别求出梯度的数值和拉格朗日乘子的数值,并更新位置.采用高斯—赛德尔迭代,循环这个过程一直到投影次数达到最大值,得到在当前时间步长内质点的最终确定位置,并根据位置随时间的变化规律,以差分的形式来估计下一时刻质点速度,预测下一时刻质点位置.循环这一过程,直至仿真结束.
3 碰撞检测
碰撞检测是虚拟手术软组织形变仿真的重要组成部分,碰撞检测的目的是精确快速的判定虚拟手术中人体器官模型与虚拟手术设备之间是否发生接触,因此碰撞检测方法对于避免穿刺和触发变形计算十分重要[18,19].为了保证虚拟手术仿真系统中生物体软组织形变仿真的实时性,本文采用快速拾取控制点的方法来进行碰撞检测,如图3所示.肝脏表面小球是由软组织物理模型的顶点数据生成的控制点,P点为手术器械前端顶点,当手术器械即将接触软组织时,P点搜索与之距离最近的控制点A.控制点A带动相邻控制点B、C、D等产生移动,使得虚拟手术器械在软组织上产生提拉、压缩等控制动作.控制点通过B-PBD算法更新每一时刻的位置,模拟软组织形变.

图3 手术器械与肝脏控制点的碰撞检测Fig.3 Collision detection between surgical instrument and liver control point
4 软组织变形实验
4.1 实验平台
虚拟手术系统平台的硬件主要包括计算机和交互(视觉交互、触觉交互)设备两部分.系统平台的触觉交互设备由美国 Sensable Technologies Incorporated(STI)公司的开发生产的Geomagic Touch的触觉反馈设备,该设备提供了HLAPI,用于触觉反馈力的计算,以实现触觉交互操作.Geomagic Touch力反馈设备具有6 自由度,160mm×120mm×70mm的三维工作空间,0.009mm的空间分辨率,3.3N的最大施加力.图形工作站是一类高性能计算设备,负责整个系统的算法计算,执行及相关逻辑处理.为了保证算法的计算速度和模型的执行效率,本课题选用的工作站具有较强的图形图像处理能力,具体性能参数如表2所示,图4为虚拟手术仿真平台硬件设备.

表2 图形工作站性能参数Table 2 Graphic workstation performance parameters

图4 虚拟手术仿真平台硬件设备Fig.4 Hardware equipment of virtual surgery simulation platform
本文开发的虚拟手术系统是在 Windows 10操作系统平台、Visual Stdio 2017的编译环境下,应用程序使用C#实现,构建在Unity3D游戏引擎上.建立的虚拟手术仿真系统可在普通的 PC 机上运行,便于后续的推广运用.按照实现的功能划分,虚拟手术仿真系统在软件层面上由三维体模型重构模块、视觉渲染模块、触觉渲染模块、切割仿真模块和辅助模块等五大模块组成.
建模数据采用Simens 64层CT扫描到的三组医疗图像,通过设定CT值将对应的组织提取出来,并利用Mimics软件进行表面三维建模.
4.2 肝脏软组织形变仿真实验与结果分析
本文对融合生物特性的位置动力学(B-PBD)形变过程进行模拟,采用肝脏组织(原始数据为肝脏CT数据)作为仿真对象.几何模型采用高精度的三角形表面网格,物理模型采用Tetgen划分的德洛内四面体网格,如图5所示.面网格中包含了14128个三角面片及7469个顶点;体网格中包含3833个四面体及1164个顶点.
4.2.1 粘弹性模型的真实性分析
1.选取模型参数
{Kg,Kn,K,τ}是建立本构方程所需参数.根据文献[20]测量的正常人体肝脏弹性系数0.3262N/mm,任意选取多组数据进行模拟仿真对比,确定了本构方程中所需参数{0.04N/mm,0.20N/mm,0.3262N/mm,218s}.
由公式(34)得出,在确定的应变情况下,λ由四面体边长决定.在X0=1.5mm,X0=2mm,以及X0=2.5mm的条件下,通过设置不同的四面体边长,求出λ值,将仿真曲线的应力值与实验数据对比,如表3~表5所示.

表3 位移X0=1.5mm时的形变力值Table 3 Deformation force at displacement X0=1.5mm

表4 位移X0=2.0mm时的形变力值Table 4 Deformation force at displacement X0=2.0mm
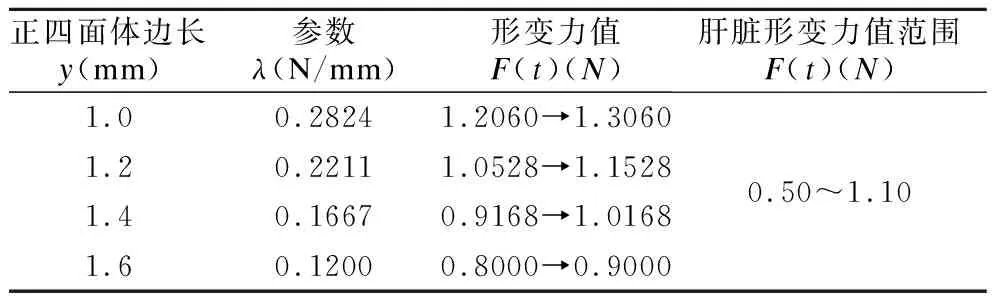
表5 位移X0=2.5mm时的形变力值Table 5 Deformation force at displacement X0=2.5mm
由表看出,当边长取1.4mm,模型应力值变化接近于肝脏应力测量值,所以本文正面体边长取y=1.4mm划分四面体网格,如图5(c)所示.
2.粘弹性分析
通过实验来验证本文建立的本构方程的粘弹性,如图6(a)为力-时间曲线,图6(b)为时间-位移曲线.
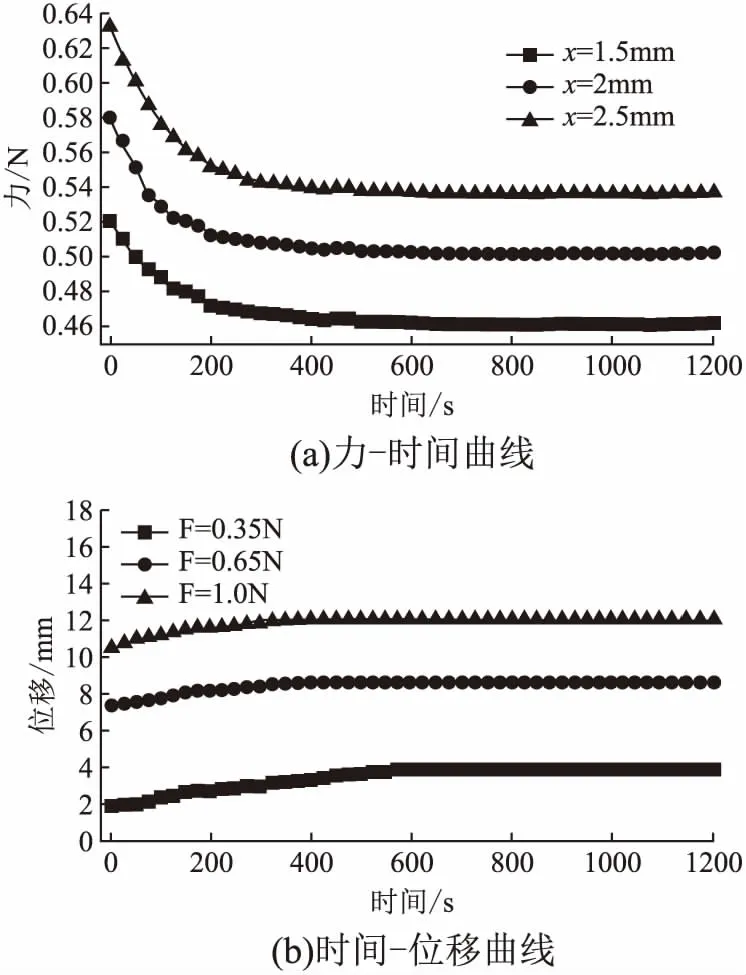
图6 粘弹性仿真曲线Fig.6 Viscoelastic simulation curve
在图6(a)中,当位移x=1.5mm,2mm和2.5mm时,外力何时间成反比关系,符合粘弹性材料的松弛规律.在图6(b)中,当F=0.35N,0.65N,1.0N时,位移和时间成正比关系,符合粘弹性材料的蠕变规律.
结果表明,本文建立的软组织三参量小变形混合填充球模型,具有良好的应力松弛特性和应变蠕变特性,符合真实软组织的变形规律.
4.2.2 软组织形变仿真的视觉效果分析
设置弹性模量、泊松比,手术器械分别对模型施加拉力和压力,基于B-PBD的方法,并采用拉伸约束和体积约束来模拟形变效果进行形变模拟,肝脏、胆囊及小黄鸭形变仿真结果如图7(a)、图7(b)、图7(c)所示.

图7 B-PBD模型及质点弹簧形变仿真Fig.7 Deformation simulation of the B-PBD and MSM model
采用质点弹簧模型(MSM)来模拟粘弹性软组织的计算步骤中,接触点附近的弹簧会产生较大的超弹性效应,出现塌陷且无法复原的现象,如图7(d)所示.通过B-PBD模型可以自然地模拟典型的软组织变形效应.从图中可以看出,使用融合位置动力学的物理模型能获得较真实的形变效果.
4.2.3 软组织形变仿真的时间效率分析
软组织形变时间长短是衡量系统实时性的重要指标,为进一步分析时间性能,采用Unity3D帧速率记录仪记录了软组织形变信息.表6反应了集中不同的软组织模型变形的时间效率,计算变形时的迭代次数为3.
本文提出的B-PBD模型与PBD、MSM模型进行了比较,MSM模型采用显式欧拉法求解运动系统;PBD模型及B-PBD模型包括拉伸约束和体积保持约束,表7为不同方法对上述肝脏模型的对比实验结果.
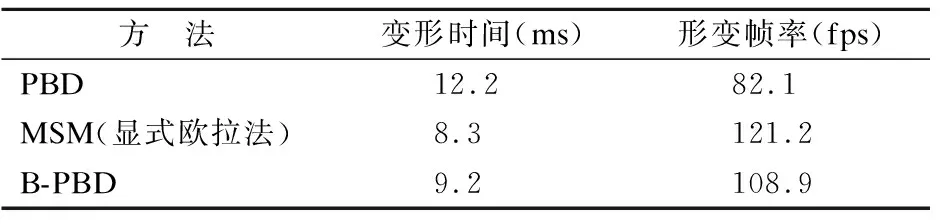
表7 3种方法(MSM/PBD/B-PBD)的时间效率Table 7 Time efficiency of the three methods (MSM/PBD/B-PBD)
本文采用控制点法进行碰撞检测,碰撞时间几乎可以忽略不计.通过实验可知,基于B-PBD方法建立的软组织模型在渲染时间和物理形变时间及帧率上都能满足实时性的要求.
4.2.4 软组织形变仿真的稳定性分析
虚拟手术应用中的软组织变形方法能否满足稳定性要求至关重要.稳定性的好坏直接影响操作者的体验和沉浸感.数值积分误差使得传统的质量弹簧法容易产生抖动现象.通过将PBD约束集成到弹簧力中,采用PBD直接控制了模型中顶点的位置,不会出现软组织不停抖动的问题,同时在三参量质点弹簧模型中控制了虚拟组织的刚度和阻尼,因此提高了模型的稳定性.类似高斯迭代的约束投影的过程使该算法接近于无条件稳定.如图8所示.将肝脏模型提拉至图8(a)所示位置,松开手术器械,使其回弹至初始状态即图8(d),通过图8(b)、图8(c)可以看出,形变回复的过程中无塌陷、抖动,稳定性较好.
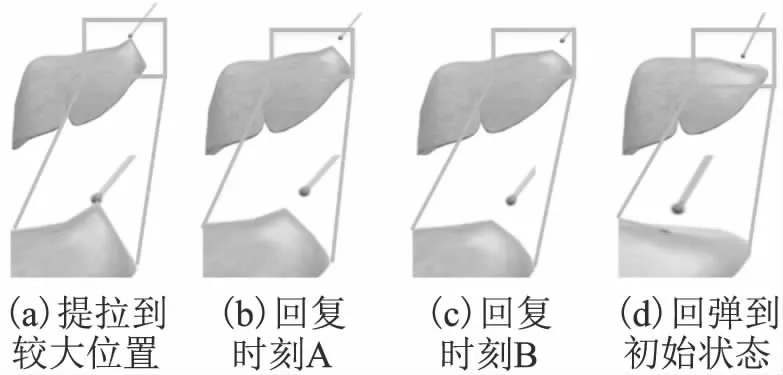
图8 肝脏模型提拉后回复效果图Fig.8 Liver model recovery after lifting
5 结 论
为了实时模拟生物软组织变形的典型力学特征,本文提出了一种将粘弹性质点弹簧(MSM)与位置动力学(PBD)集成的新方法.根据MSM和PBD都是通过空间离散质点的运动位置来模拟形变特征的共通点,并根据扩展PBD算法的推导过程,将两种模型进行整合,即基于生物特性的位置动力学(B-PBD).在这种方法中,基于牛顿第二定律采用显示欧拉法进行质点下一时刻的位置预测,改进的三参量质点弹簧的弹簧力和外力与PBD约束函数产生的约束力相结合,通过约束修正质点位置.
针对改进的三参量模型进行数据仿真,模拟出合适的四面体边长,并有针对性的构建了力时间和位移时间方程,验证了生物力学的粘弹性特性.采用胆囊、小黄鸭和肝脏模型进行力反馈实验,并进行了时间效率和稳定性分析.展示了B-PBD方法在保证视觉效果的情况下,具有更高的稳定性.同时在单线程核心计算下,碰撞检测、形变计算及渲染的整体时间能满足实时性的要求.实验表明,该方法成功地通过多种约束条件来控制软组织的变形行为,优于目前主流实时形变模拟方法,可以满足虚拟手术的需要.

