基于Space L的公共交通网络拓扑结构特性分析

王天睿,刘国睿,杨海华,陈文星,温忠海

(1.浙江省数智交院科技股份有限公司,浙江 杭州 310000;2.哈尔滨市公安交通管理局,黑龙江 哈尔滨 150040;3.中国建设基础设施有限公司,北京 100000;4.济南金衢公路勘察设计研究有限公司,山东 济南 250000;5.哈尔滨交研交通工程有限责任公司,黑龙江 哈尔滨 150040)

0 引 言

公共交通系统是一个复杂系统,研究复杂公共交通网络的拓扑结构特征对缓解复杂公交网络存在的问题具有重要意义[1-2]。从理论上来讲,运用复杂网络理论研究城市公交网络结构已经成为未来公交网络优化的发展需求,为探索城市公共交通网络演化机制和科学规划公交网络结构提供了理论指导。从方法论的角度来看,将复杂网络理论和公交网络相结合,是寻找缓解城市公交网络问题的较好途径。李婧怡等[3]通过Space L构建了基于车辆分布的公交动态复杂网络模型,用于动态分析公交车辆在线网上的实时分布。韦胜等[4]发明了一种基于多重映射的公交网络枢纽评价方法,能够在考虑空间距离约束下公交站点需要合并问题解决的基础上,对重要的公交枢纽站点和枢纽线路进行识别。罗钧韶[5]提出了一种基于GIS的城市公交复杂网络特征分析决策平台,可以用于分析公交网络涉及站点可达性。赖强等[6]基于Python构建了公交网络拓扑结构模型,基于复杂网络理论对城市公交网络鲁棒性进行分析与优化,最终发现低度数和低介数加边策略对网络鲁棒性提升效果好。刘飞[7]根据复杂网络建模理论基于耦合映射格子(CMLs)模型提出了双层复杂网络节点和连边的级联失效模型,以脆弱性表征极端天气对城市公共交通系统造成的不利影响。张琳等[8]基于复杂网络理论和空间信息嵌入,给出基于ArcGIS的耦合站点定量化判定规则和流程化处理方法,建立复合网络脆弱性改进分析模型。

因此,将复杂网络理论应用于公共交通网络拓扑结构分析不仅具有重要的理论价值,而且具有重要的现实意义。

1 复杂网络拓扑特性参数[9]

(1)节点度

(1)

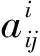
(2)节点强度

(2)

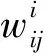
(3)边权

Sij=∑lij

(3)

式中:Sij为边权,为两个节点间承担的线路数;lij为两节点间线路条数。

(4)特征路径长度

(4)

式中:L为特征路径长度,为网络中任意两个站点之间最短路径上的平均公交站点数;dij为任意两节点间的最短路径。

(5)聚集系数

Ci=2Mi/[ki(ki-1)]

(5)

式中:Ci为聚集系数,为通过某站点的线路间的站点之间的联系;Mi为节点i连接边数,ki为与i相连的节点。

2 L空间网络构建方法

Space L网络是以节点表示公交站点,如果两个公交站点在同一条线路上且彼此相邻,则这两个站点相连[10];对于一个如图1所示具有6条公交路线(数字)和8个公交车站(字母)的示意性公交系统,根据三种模型定义,可以得到如图2所示的邻接矩阵。

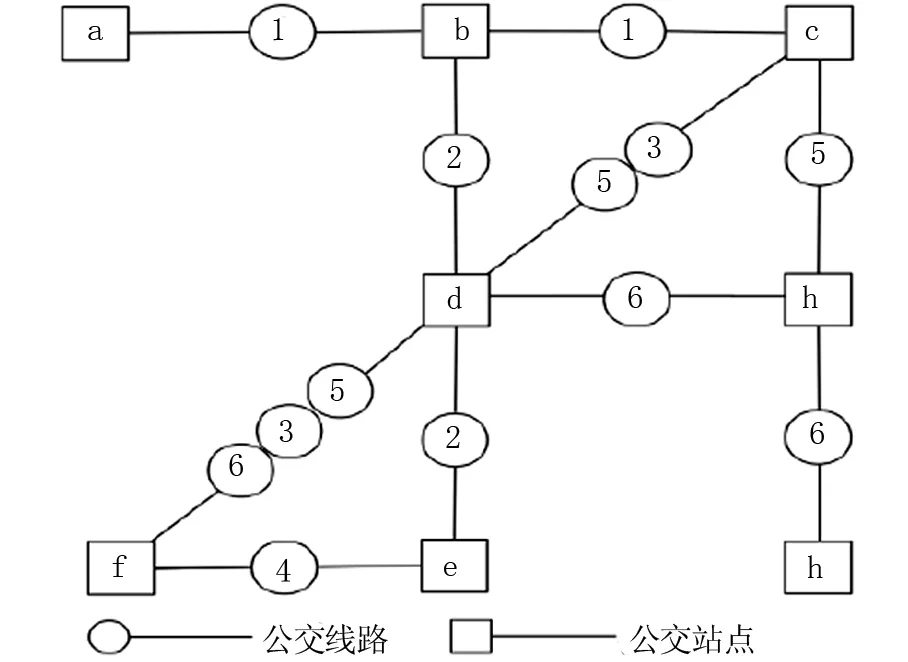
图中数字表示不同公交路线;字母表示不同公交车站。

图2 邻接矩阵

3 数据获取

以成都市常规公交网络为例进行网络拓扑结构分析。目前,成都市常规公交有142条,公交站点1 653个。通过网址(http://www.8684.cn/)下载成都公交信息数据库,并通过数据库软件进行数据解析,统计成都市的公交线路名称、公交车站名称、公交上、下行线路依次经过的站点序号等。

4 成都市公交网络特性分析

4.1 公交线路上下行差异性分析

城市公交网络通常被描述为一个无向的复杂网络,即每条线路的上行和下行是相同的。随着城市规模的扩大,一些旧城区的路网不断调整。例如,为了适应交通量的增长,许多路段被改造成单行道。与路网相一致,部分公交线路出现了上行和下行不一样的情况。模拟的公交上、下行线路的走向如图3所示。

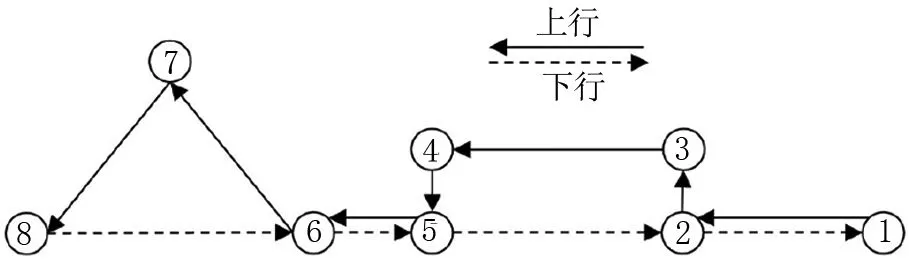
图3 模拟公交上下行线路走向

从图3中可以清楚的看出该条公交线路的上下行差异是比较大的,为了测量公交线路上的上行和下行站点之间的差异,提出了公交线路重复因子的概念,其是指一条线路上的上行和下行方向上的重复站点与该线路的比率。线路的上行和下行不同站点数量越多,重复因子越大;当线路的上行和下行完全相同时,重复因子为1。

DFi=RNi/SEi

(6)

式中:DFi为一条线路的重复因子;RNi为一条线路上、下行方向上重复站点的数量;SEi为一条线路上、下行方向上所有站点的数量。

根据公式(3)可以计算出成都市所有公交线路的重复因子。成都市有91%的线路重复因子在不同程度上小于1,重复因子小于0.8占比达到59%,即成都市公交上、下行线路的差异比较明显。

4.2 基于Space L的拓扑结构特性分析

利用MATLAB进行网络拓扑特性分析,拓扑指标主要包括节点度、节点强度、边权和点权、特征路径长度、聚集系数。

(1)节点度

从图4(a)图中可以看出,在L空间下成都市上下行站点差异性并没有对度分部产生很大影响。节点度的累积分布更符合指数分布的累积分布类型。度值为2的节点约占总站点数的60%左右,说明半数以上站点仅与前、后站点相连。成都公交车站点平均度均为2.63,即每个公交车站一般与2～3个其他车站相连,可见只有少数节点具有很高的度。图4(b)为考虑原始数据的度的累积概率分布[11],从中可以看出,公交站点连接网络几乎成指数函数的趋势,上行拟合为y=0.6959e-0.64x、下行为y=0.5993e-0.597x。

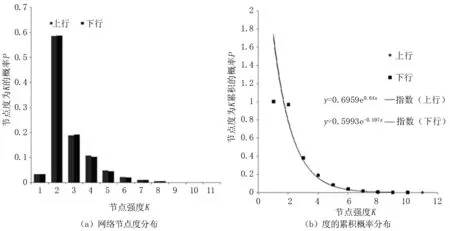
图4 网络节点度和度的累积概率分布

从表1和表2可以看出,这些站点通常是网络的核心节点,一般是公共交通网络的枢纽。节点度最大的12个站点中有5个不同,分别是青羊宫、总府路、大业路、高笋塘、动物园、九茹村、塔子山公园、金沙公交站、人民中路二段、二环神仙树路口。这10个公交站点度的上行与下行大小如图5所示。

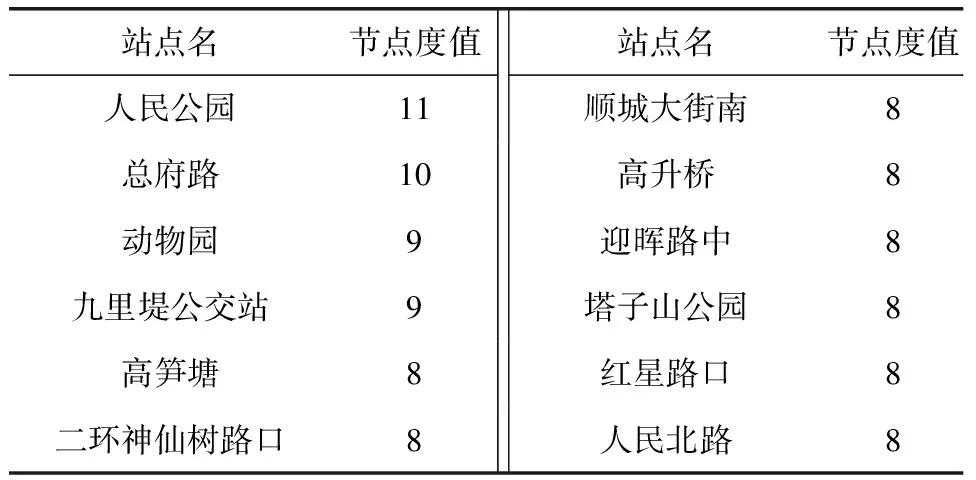
表1 成都市上行公交站点网络度值排名

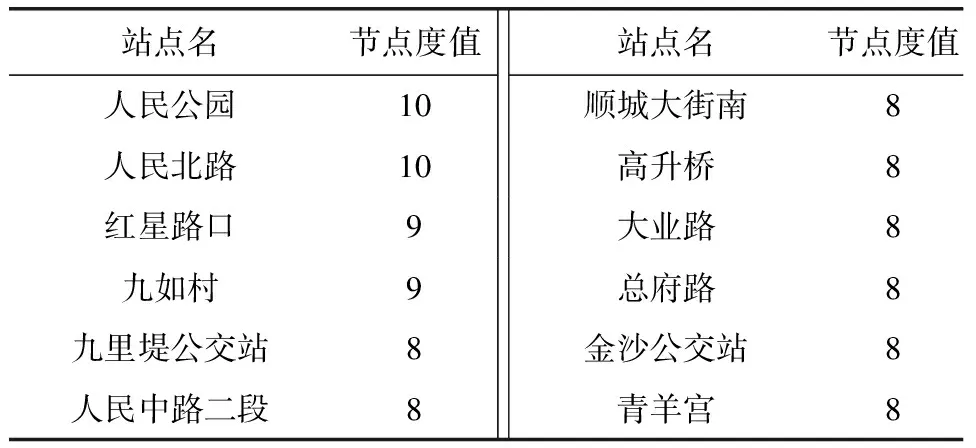
表2 成都市上行公交站点网络度值排名

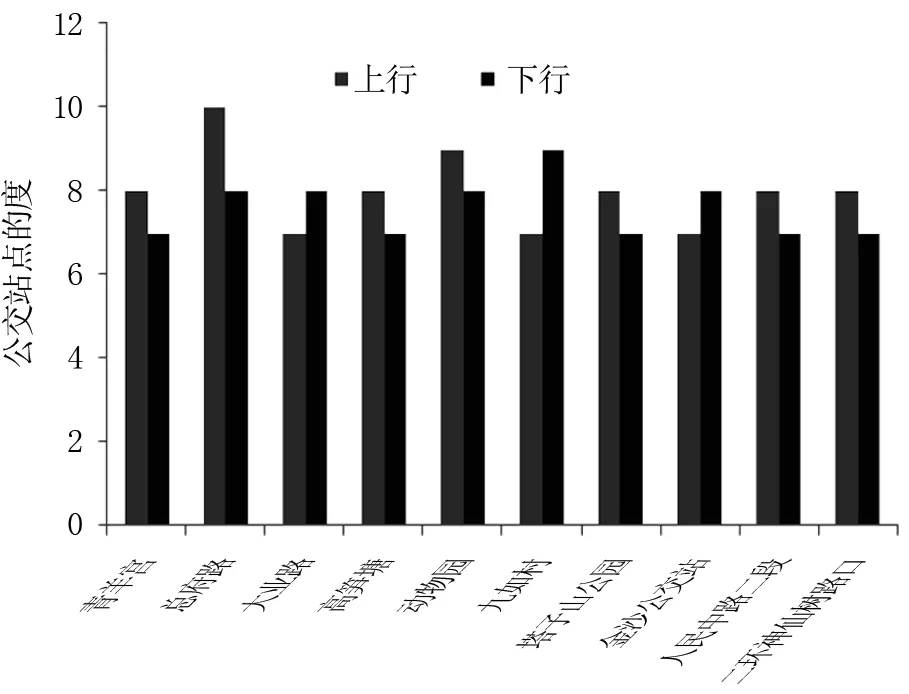
图5 上行与下行公交站点的度

(2)节点强度

为了更直接反映上下行公交站点的差异,赋权无权网络为加权网络[5]。节点的强度是站点所有边的边权之和,体现了该站点在网络中的地位。

从图6(a)中可以看出,节点强度与度有类似的变化规律,上行和下行节点强度概率分布几乎一致。从表3、表4中的强度值可看出,上行与下行具体每个站点节点强度有所差异,这主要是由于上下行经过站点及其每个站点上下行中经过的线路不同导致的。节点强度不超过2的数量占到了47%。平均强度上行为4.934、下行4.945,表明通过每个站点的线路为2～3条。权最大的站点是高笋塘站,其作为枢纽站是公交网络的关键节点;少数站点具有强的吸引力,汇集了大量线路,即“富人俱乐部特性”[12]。

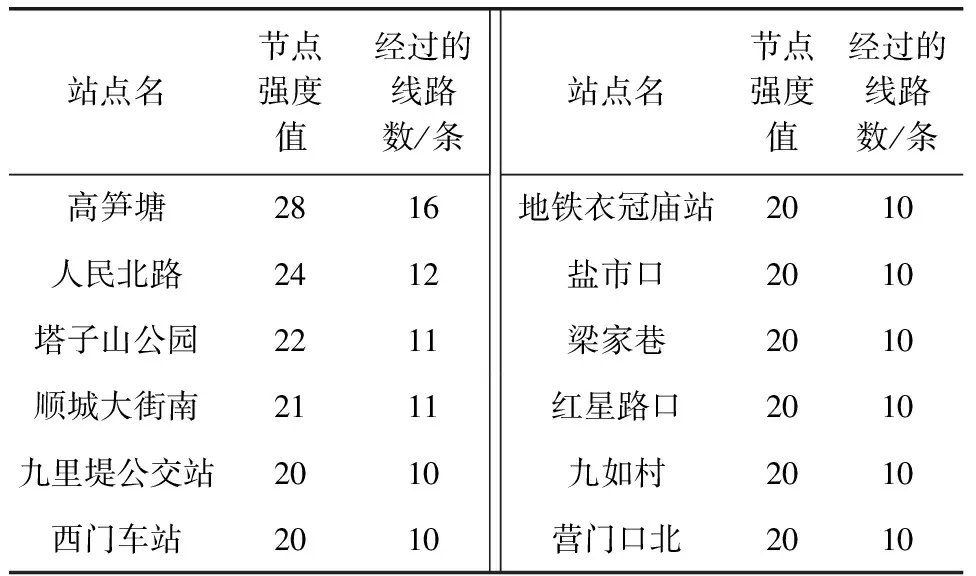
表3 成都市上行公交站点节点强度值排名

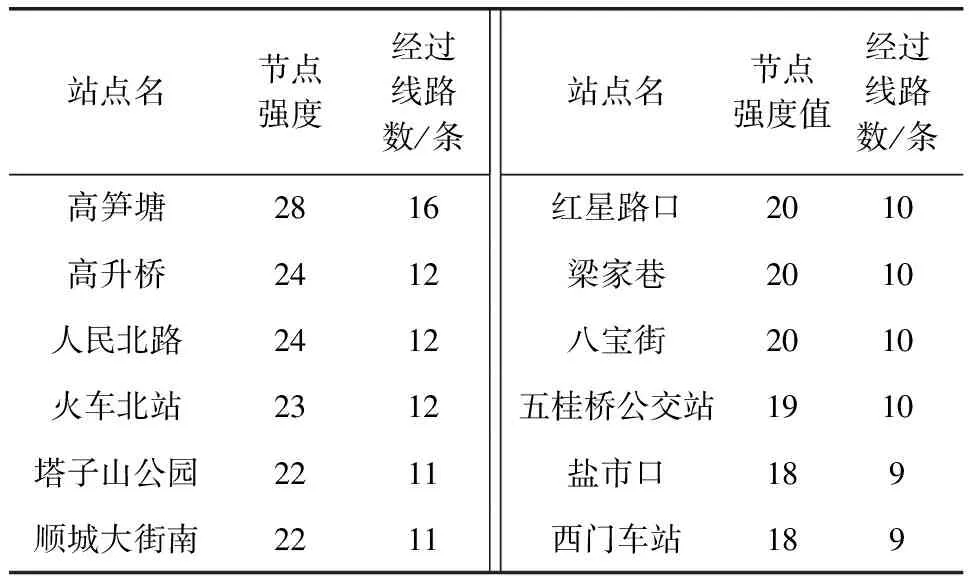
表4 成都市上行公交站点节点强度值排名

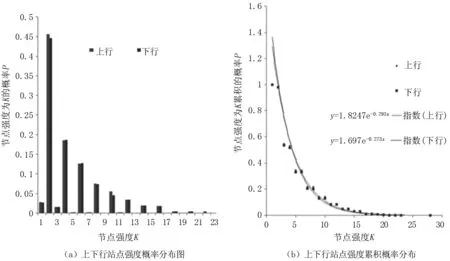
图6 上下行站点强度概率和强度累积概率分布

从表3和表4中可以看到,这些节点通常是网络的核心节点,一般是公共交通网络的枢纽。节点度最大的12个站点有3处不同,分别是高升桥、八宝街、营门口北、九里堤公交站、地铁衣冠庙站。这6个公交站点上下行强度大小如图7所示。

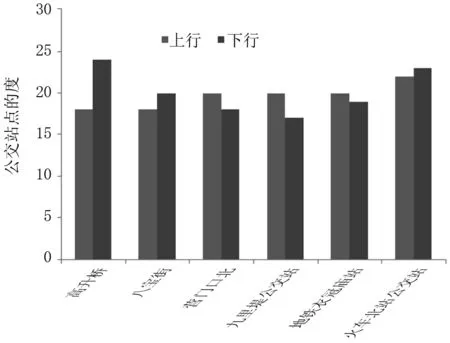
图7 上行与下行公交站点强度

(3)点权与边权

边权反映了节点间路段承载的线路数,反映了路段在网络中的重要性。根据下载网络数据统计得到成都公交网络的边权均值为1.98,说明2个相邻站点平均可以与2条线路相连连。最大边权为20,为高笋塘—火车北站公交站路段,表明该区域可提供20种出行路线。

(4)特征路径长度

实证统计结果表明,成都市空间网络特征路径长度上下行均为17,说明成都公交出行最短路径平均为17站;公交网络直径为62,说明两节点间出行距离最大长度为62,网络中的最短路径可能太长。

(5)聚集系数

成都公交网络的平均聚集系数为0.067 8,系数较大,同时网络中平均最短路径较小,这两个特征表明成都常规公交网络具有“小世界现象”[13]。

5 基于Space L的公交网络鲁棒性分析

对成都Space L空间网络中进行随机攻击和蓄意攻击,分析网络的鲁棒性。这里的随机攻击是指随机删除网络中的节点,而恶意攻击是指对网络中的站点进行选择性攻击,实验按节点度由大到小的顺序进行。当网络出现故障时,部分或全部的节点特征值将发生变化。可以通过最大连通子图大小的变化来反映网络结构和性能的变化。研究表明,当最大连通子图的相对尺寸小于50%时,网络功能几乎处于瘫痪状态[14]。利用MATLAB对成都公交网络的最大连通子图进行分析,每删除一个节点,重新计算节点度,然后再删除具有最大度值的节点,这可以更好探索网络结构和功能之间的关系。

成都公共交通网络在公交站点随机攻击和基于节点降序的蓄意攻击情况下的鲁棒性如图8所示。可以看出,面对节点的随机攻击,最大连通子图S大小均匀减小,并且没有跳跃式下降。当f=0.74时,S=0,s=1。这反映了成都的公交网络对随机攻击具有良好的鲁棒性。当进行蓄意攻击,成都市停靠站点网络中的节点数量下降9%时,最大连通子图大小急剧下降到原始大小的一半,网络功能同时接近瘫痪,这反映了成都公交网络的抗攻击能力较弱。因此,成都市公交网络中的148个度值为6以上的站点,如人民公园,人民北路,总府路和动物园等,对整个公交网络系统的有效运行起着至关重要的作用。

6 结 论

在L空间下,成都市公交网络上行与下行公交站点的差异性并没有对成都市整个公交网络各个基本参数产生很大的影响。L网络具有聚集系数大和特征路径长度小的特征,即“小世界特征”;L空间网络的节点度的累积分布呈现幂指形式,即是一个随机进化增长网络;从点权边权可以看出,高笋塘—火车北站公交站路段为重要线路,可以考虑布局换乘枢纽。成都市公交网络鲁棒性分析表明,人民公园,人民北路,总府路和动物园等站点对整个公交网络有效运行起着至关重要的作用。