基于变分BP神经网络的普通公路轴载计算

刘 坤,张路凯,孙 满,撒 蕾,王英平,张金萌

(1.徐州市公路事业发展中心,江苏 徐州 221006;2.交通运输部规划研究院,北京 100029)

公路轴载是指因车辆轴荷负担对路段表面及内部造成的压损影响,主要量化指标包括轴载谱和当量轴次。公路养护管理与运营组织中,轴载量是其决策分析的重要依据,用于衡量路段重载交通的服务质量状况、性能衰减速率和时空分布特征。相较于高速公路的全样本车辆称重,普通公路普遍缺乏车重轴载检测设备,因而其轴载量多以推算和评价为主。当前关于普通公路轴载量的研究热点中,在研究内容上集中于多场景多精度轴载谱估计和累计当量轴次规律分析等,在研究方法上主要以边缘预测推算模型和小样本多主体评价模型为主。李志勇等[1]通过现场取样测试分析了重载车辆荷载的分布范围及变化规律,并建立了路基结构动应力变化模型。宋尧等[2]基于车辆荷载样本调查和荷载试验分析了重载交通公路桥梁的荷载性能,并根据规范标准提出了改进措施。张承亮[3]计算了轴荷分布系数区间和累计轴载当量,以此分析沥青路面抗滑性能衰减规律。马建国等[4]依据呼包公路路面结构建立ANSYS有限元分析模型,进而计算多类轴荷的取值。贾志超等[5]基于实测调查交通量数据建立参数数据库,分析了交通量变化及轴载谱参数之间的关系。吴正光等[6]基于正态分布模型表征该路段单轴双轮轴载谱,研究了该路段交通荷载参数和货车超载情况。李佳等[7]建立了回归分析模型,从数据校验角度对比分析了连续式交通调查数据与轴载调查数据的差异。彭芳文等[8]构建了路面性能衰变“负指数”模型和影响因子生长曲线,用以分析轴载量对公路使用寿命和养护特性的影响。

既有研究成果中,多以调查样本的趋势外推作为依据,计算并分析轴载量变化规律,未重视数据驱动推算的应用。同时,在计算方法上也未涉及“多输入多输出”的特征,未充分体现数据融合的作用效果。鉴于此,提出基于变分BP神经网络的普通公路轴载计算。考虑普通公路相较于高速公路的轴重数据盲区,以交通流量调查数据为输入,建立变分BP神经网络推算模型,依托样本数据集的训练、验证和测试,计算获得路段的轴载谱和当量轴次,并依托江苏徐州公路网的重载交通监测工程进行落地实践。

1 问题描述

首先,结合实际调查统计场景,阐述公路轴载量化指标的计算定义,包括轴载谱和当量轴次[9]。之后,分析普通公路的数据支撑缺陷,明确基于样本数据推算的方法原则。

1.1 轴载计算定义

轴载谱的定义为不同类型车辆的不同轴型在不同轴重区间所占的百分比,即不同轴型的轴重分布系数。基于实际调查统计流程,提出轴载谱计算结构如公式(1)所示。

ALDFmij=NDmij/NAmi

(1)

式中:m为车型索引变量,表示根据单轴、双联轴和三联轴等不同轴型组合的各类车辆;i为轴型索引变量,分别为单轴、双联轴和三联轴;j为轴重区间索引变量,单轴、双联轴和三联轴分别间隔2.5、4.5、9.0 kN;ALDFmij为路段断面统计中第m类车辆中第i种轴型在第j级轴重区间的轴重分布系数;NDmij为路段断面统计中第m类车辆中第i种轴型在第j级轴重区间的作用次数,次;NAmi为路段断面统计中第m类车辆中第i种轴型的总作用次数,次。

上述解析式为轴载谱的相关计算定义。进一步地,当量轴次表示单轴轴荷与标准轴荷(100 kN)等效的压力次数。基于实际调查统计流程,提出当量轴次计算步骤如下。

(1)计算各类车辆中不同轴型平均作用次数

根据各类车辆中单轴、双联轴和三联轴的作用次数统计量,除以各类车辆总数量,即可获得各类车辆中不同轴型的平均作用次数,如公式(2)所示。

NAPTmi=NAmi/NTm

(2)

式中:NAPTmi为第m类车辆中第i种轴型的平均作用次数,次;NAmi为路段断面统计中第m类车辆中第i种轴型的总作用次数,次;NTm为路段断面统计中第m类车辆的总数量,辆;m为车型索引变量;i为轴型索引变量,分别为单轴、双联轴和三联轴。

(2)计算各类车辆中不同轴型在不同轴重区间的当量轴次

取各轴重区间中点值作为该轴重区间代表轴重,计算各类车辆各种轴型在不同轴重区间的当量轴次,如公式(3)所示。

EALFmij=c1c2(Pmij/Ps)b

(3)

式中:EALFmij为第m类车辆中第i种轴型在第j级轴重区间的当量轴次,次;c1为轴组系数,前后轴间距大于3 m时,分别按单个轴计算;轴间距小于3 m时,双联轴取2.1,三联轴取3.2;c2为轮组系数,双轮组取1.0,单轮组取4.5;Ps为路面设计轴载,kN;Pmij为第m类车辆中第i种轴型在第j级轴重区间的单轴轴载,kN;b为换算指数。分析沥青混合料层疲劳和沥青混合料层永久变形时,b=4;分析路基永久变形时,b=5;分析无机结合料稳定层疲劳时,b=13。

(3)计算汇总各类车辆的当量轴次

在以上参数基础上,进一步计算各类车辆的当量轴次,如公式(4)所示。

EALFmij=

(4)

式中:EALFm为根据路段断面统计数据所计算的第m类车辆的当量轴次,次;EAPTmi为第m类车辆中第i种轴型的平均作用次数,次;EALFmij为第m类车辆中第i种轴型在第j级轴重区间的当量轴次,次;ALDFmij为路段断面统计中第m类车辆中第i种轴型在第j级轴重区间的轴重分布系数。

1.2 推算方法流程

公式(1)～公式(4)即为基于实际调查统计的公路轴载计算流程。在全样本覆盖的数据支撑下,可直接计算所需的轴分布系数与当量轴次。然而,由变量定义和计算公式可知,轴重轴荷是其中的关键数据源。对于普通公路,往往只有少量路段布置有人工治超预检站,非现场执法动态卡点和轴载调查站,数据支撑条件较为薄弱。另一方面,普通公路路段自动化交通情况调查设备分布较广,覆盖比例较大,可考虑作为全样本的辅助输入数据源。综上,提出交调数据与轴载数据相融合的推算流程,依托有限样本条件,基于变分BP神经网络模型获取输入与输出之间的结构关系,实现轴载数据盲区的目标推算,总体流程如图1所示。

2 基于变分BP神经网络的轴载推算模型

以少量具有轴载数据的普通公路路段作为样本,依据公式(1)～公式(4)计算轴载谱和当量轴次。此外,分析交调与轴载的车型对应关系如表1所示。推算实施中,按照输出目标轴载的车型,设定对应交调数据源的车型。

进一步地,建立数据模型以实现轴载数据盲区路段的轴载谱与当量轴次推算。人工神经网络具有类似于人类大脑功能的学习训练特征,可被用来实现参数预测和模式识别。其基础构成单元为众多的神经元,基本原理在于模拟神经对信息的并行处理,形成多元多线程多触发规则的记忆训练结构[10]。其中,BP(前向反馈)神经网络是当前较为成熟的结构模型,可进一步在基础模型中引入数值变分修正。如图2所示,变分BP神经网络的主要组成特征量包括网络层数量、神经元数量以及神经元之间的连接边权。作为多层前馈网络模型,其核心学习规则为反向传播的变分误差算法。模型结构中包括三类神经元层,即输入、隐含及输出。通过误差在各层之间传播的持续修正,网络输入与输出之间的关联结构逐渐被完善。变分BP修正算法的关键计算在于误差数值的变分梯度方向下降,以此确保模型中误差按照最速下降趋势变化。以三层变分BP神经网络模型为例,其神经元连接权值与传递信号触发阈值的调整规则函数如公式(5)所示。

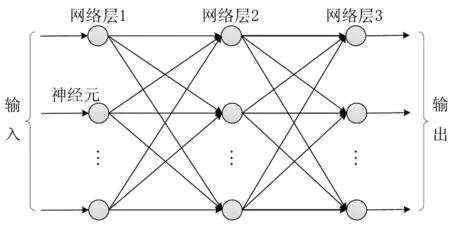
图2 变分BP神经网络结构

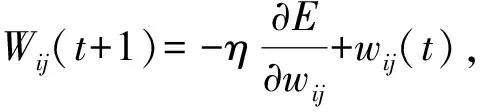
(5)

式中:E为网络输出数据与实际样本数据间的误差平方和;η为网络中学习速率,即连接权值的修正幅度;wij(t)为在t时刻输入层第i个神经元连接隐含层第j个神经元的权值,而wij(t+1)为在t+1时刻的相应权值;wjk(t)为在t时刻隐含层第j个神经元连接输出层第k个神经元的权值,而wjk(t+1)为在t+1时刻的相应权值;Bij(t)、Bij(t+1)、Bjk(t)以及Bjk(t+1)分别为各层神经元在t时刻和t+1时刻的变化阈值。

上述内容即为所构建变分BP网络的学习规则。实际推算中,当神经元的激励函数连续可导时,可求得∂E/∂wij与∂E/∂wjk的表达式。

对于普通公路样本路段,变分BP神经网络模型的输入为交调数据中各类车型对应的流量,输出数据为轴载谱和当量轴次。同时,样本数据中区分训练集和验证集,以实现推算的误差判别。最后,以覆盖交调数据的轴载数据盲区路段作为测试集,应用变分BP神经网络推算轴载谱和当量轴次,模型的具体流程步骤如图3所示。

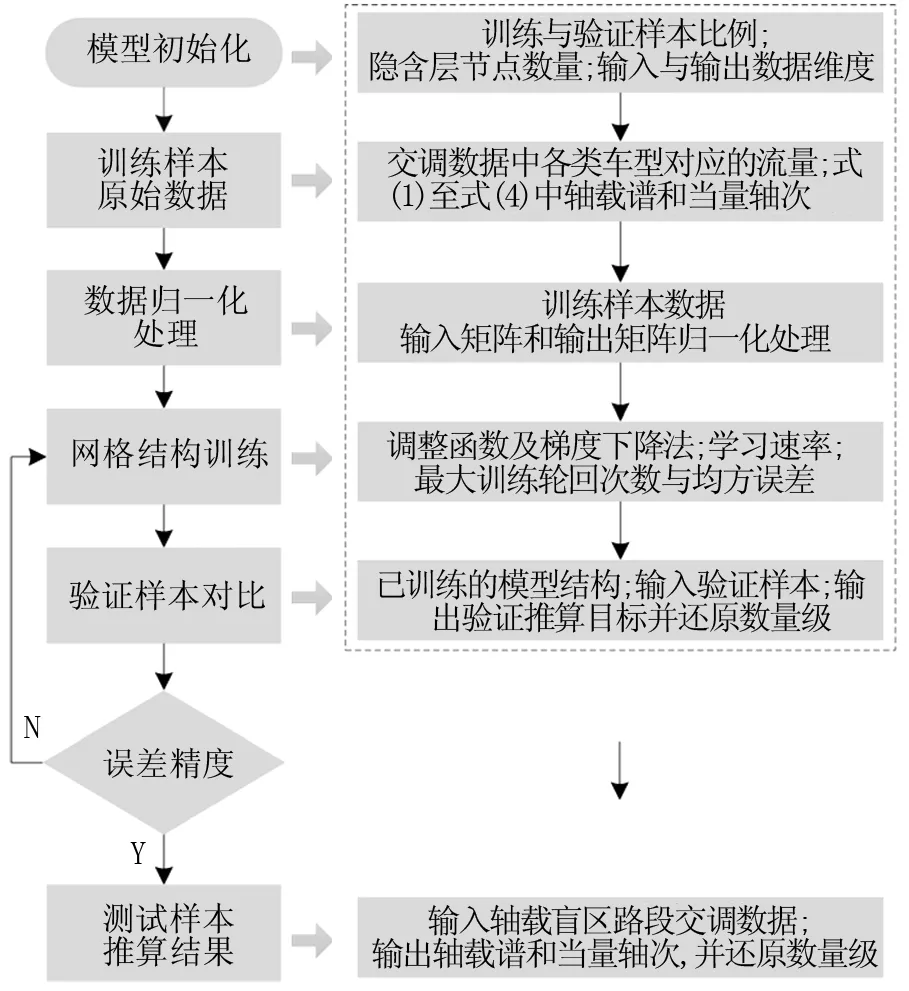
图3 变分BP神经网络模型实施流程

3 实例研究

以江苏省徐州市普通公路网为对象进行研究。涉及359个交通情况观测调查站、2个轴载检测调查站。样本设定中,选取2021年9月1日至9月30日的连续日数据。训练样本包括1号轴载检测调查站对应的轴载数据与交调数据,验证样本为2号轴载检测调查站对应的轴载数据与交调数据,测试样本为其他普通公路路段的交调数据。变分BP神经网络模型设置中,隐含层数量为3,神经元节点数分别为3、7和2,轮回周期数为10,学习速率设置为0.05,最大训练次数为5 000,均方误差为0.000 65。

推算的实施环境条件为MATLAB R2019b与SQL Server 2017。

表2为验证样本的当量轴次计算结果,包括2号轴载检测调查站路段的实际值与推算值。为了对比所建立变分BP神经网络模型的推算效果,同步采用多元线性回归模型和灰色系统预测模型进行计算。对于当量轴次总计结果,所建立模型结果与实际数值的偏差为17.15%,优于多元线性回归模型(22.37%)和灰色系统预测模型(19.89%)。从方法本身特点来看,变分BP神经网络模型通过足量的学习过程以实现最大化的“输入-输出”精度,其内部结构的适应性更为灵活复杂;多元线性回归模型主要从线性维度对大量的自变量进行拟合,回归处理的结构性方法较为单一;灰色系统预测模型从样本的数据表层特征入手进行挖掘,获得隐藏的数值趋势规律,训练复杂度介于BP神经网络模型和多元线性回归模型之间。相较于其他两种模型,所建立模型在2轴、5轴和6轴车推算结果方面具有更好的精度。其原因在于3轴、4轴车的车型较为分散,且半挂车的比例较大,单轴的轴荷规律性较弱,数据归一化难度较2轴、5轴和6轴车更大,不易体现出神经网络多层神经元的学习训练优势。从横向结果看,三种模型下6轴车的推算精度均最低。其原因在于6轴车的车型主要包括特大货车和集装箱车,受实际硬件条件影响,二者的轴载检测结果往往存在一定的浮动区间。

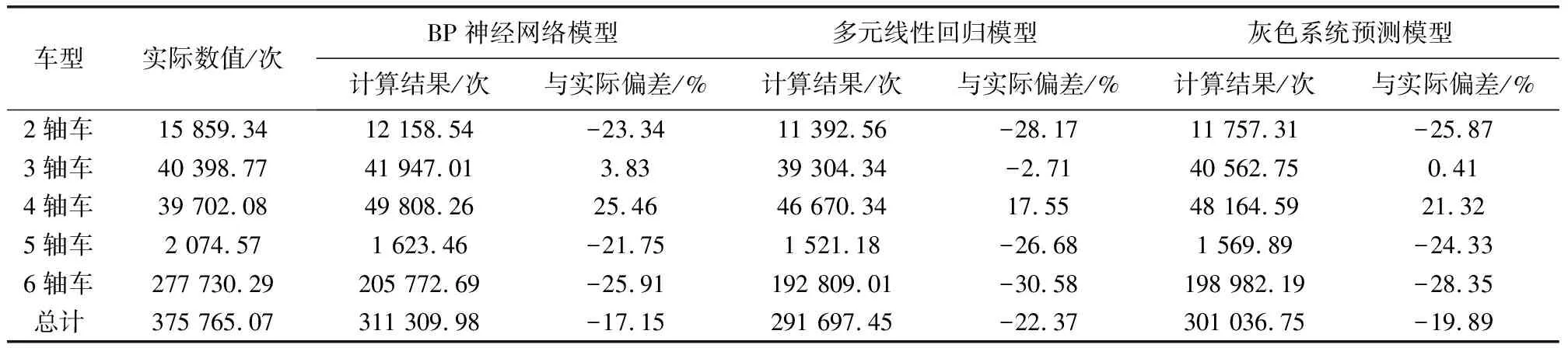
表2 验证样本实际当量轴次与推算当量轴次对比

图4为验证样本的轴载谱计算结果,包括2号轴载检测调查站路段的实际值与推算值。相较于当量轴次推算计算的“多输入-单输出”特点,轴载谱的推算需满足“多输入-多输出”要求,因此多元线性回归模型和灰色系统预测模型均不适用。从实际值与推算值的对比可以看出,二者总体趋势和分布规律大致相当,推算精度较为理想。为了进一步量化分析推算精度,对各轴数车型的实际值与推算值偏差进行计算,并整理偏差的相关判据指标如表3所示。整体来看,各轴数车型轴载谱的推算结果与实际结果较为接近,且大致浮动区间与当量轴次结果类似。具体而言,3轴车轴载谱的推算结果精度明显高于其他车型。其原因在于,当前货车市场中3轴车虽然半挂车比例较高,但各子车型对应的额定载重较为一致,推算难度较小。

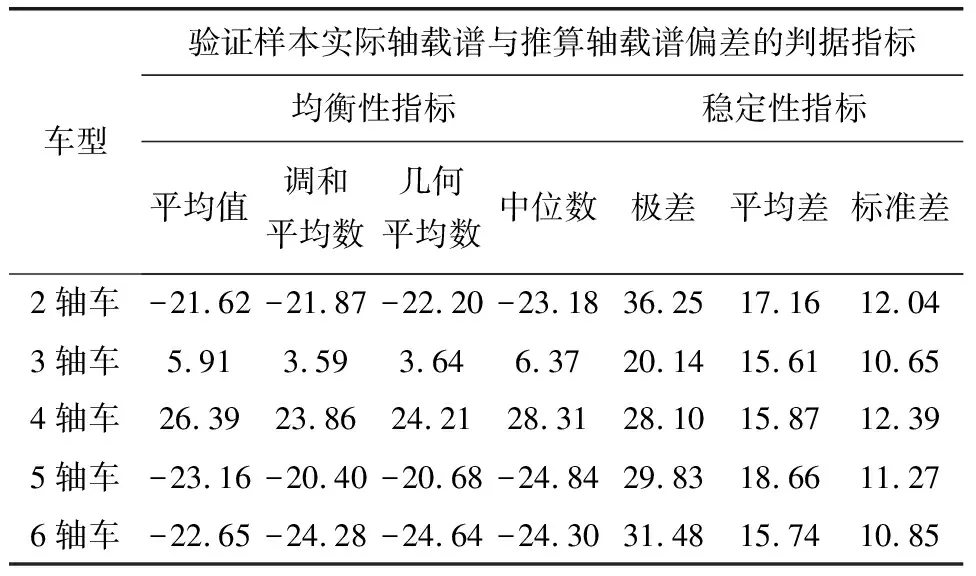
表3 实例研究中方法对比的计算结果 单位:%

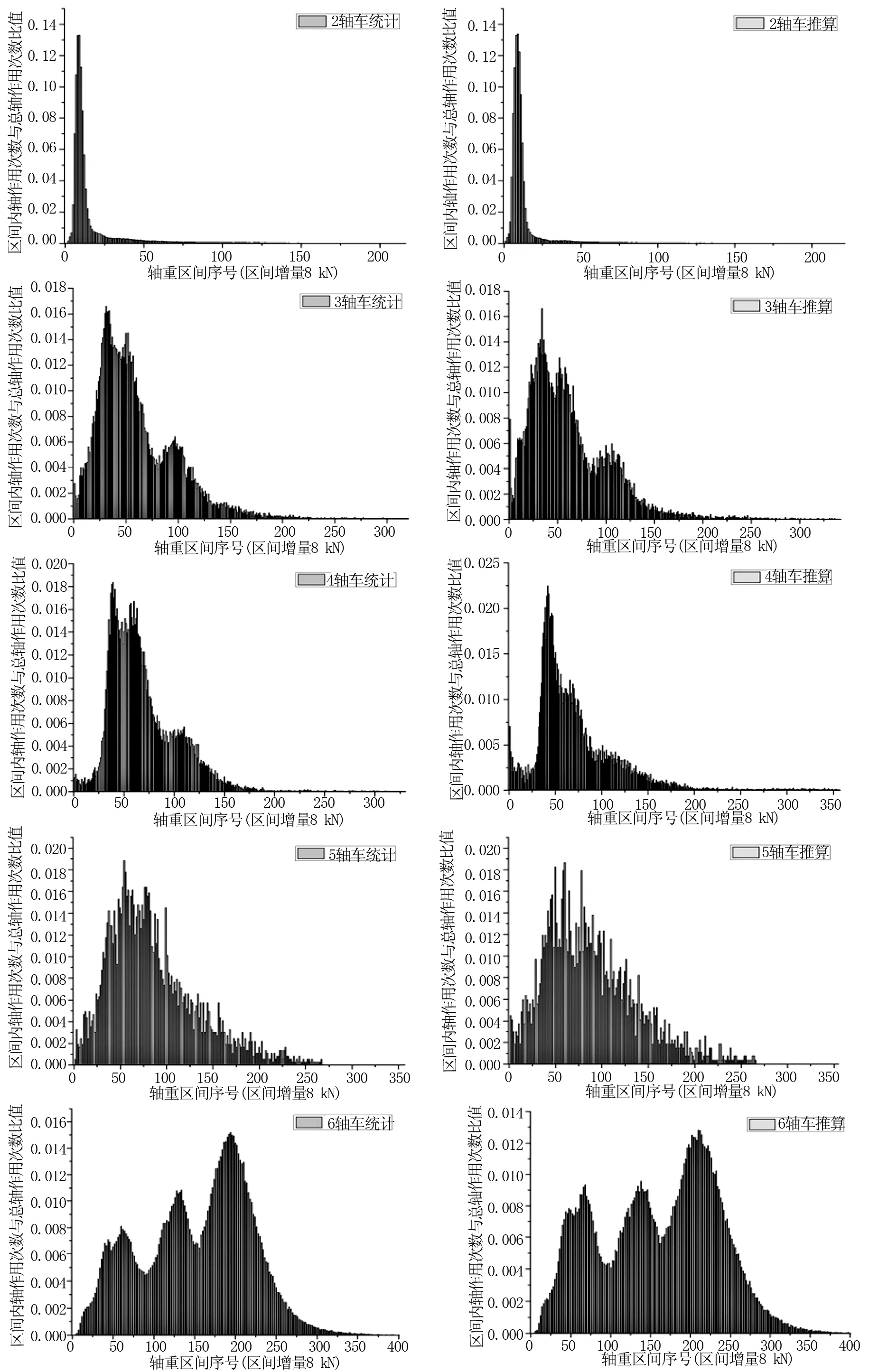
图4 验证样本实际轴载谱与推算轴载谱对比

在推算精度分析的基础上,进一步对徐州地区普通公路网总体的轴载谱和当量轴次进行推算,即计算其余357个交调站路段的相关数据。图5为各车型下平均的轴载谱推算结果,可作为区域路网运行状态的分析参考。当量轴次推算中,考虑重点月份跨度对结果的影响,同时计算了2021年9月和10月的结果,如表4所示。两个月的当量轴次中,车型分布趋势基本一致,且10月份数值高于9月份相应数值,总体规律符合实际情况。

表4 徐州地区普通公路路段平均当量轴次推算结果 单位:次

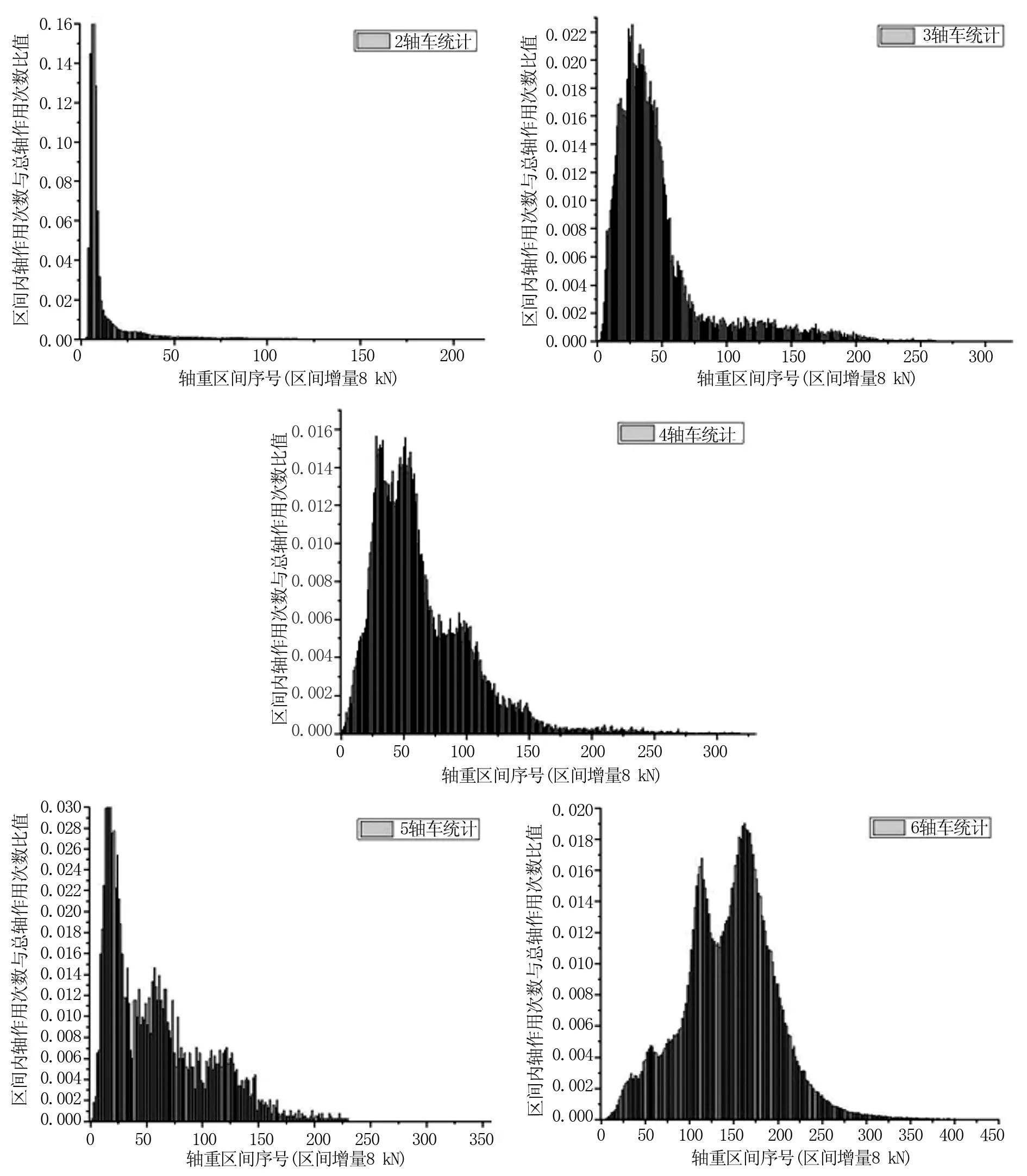
图5 徐州地区普通公路路段单轴平均轴载谱推算结果

4 结 论

(1)基于设计规范明确了路段轴载谱和累计当量轴次的计算需求,针对行业数据资源现状分析了多输入多输出的数据资源驱动特征,考虑多元耦合的计算流程构建了变分BP神经网络模型。

(2)以徐州地区普通公路网为实例进行分析,验证集在回归效果、学习速率、梯度精度等方面表现出较好性能,所得月度当量轴次的推算偏差为17.15%,优于灰色系统预测模型偏差结果(19.89%)以及多元线性回归模型偏差结果(22.37%);轴载谱的推算结果中,3轴车的精度明显高于其他车型。

(3)所建立的变分BP神经网络模型中,未分析自变量之间的多重共线性特征,在数据样本较小的情况下可能导致因变量之间的叠加误差。下一步研究中可考虑数据降维流程,例如引入Logistic回归预先对变量进行分类处理。