联合天线选择与用户调度的大规模MIMO系统能效优化算法

张馨月 杜飞 范静怡 耿绥燕 赵雄文

（华北电力大学电气与电子工程学院, 北京 102206）

0 引 言

随着5G 移动通信技术的快速发展，以及下一代通信技术后5G(beyond 5G，B5G)、6G[1]的研究深入，全球范围内的移动用户数和高速数据业务呈爆炸式增长，移动通信系统的能源消耗越来越来大，仅以通信系统容量最大化为主要性能指标已无法满足当今通信系统的设计需求.因此，“能效”成为了5G 新标准的关键性能指标之一，对实现绿色通信具有重大意义.作为5G 的核心技术之一，大规模多输入多输出(multiple-input multiple-output，MIMO)技术通过在基站端部署大规模天线，在同一时段内向多个用户提供通信服务，大幅度提升了系统的频率效率，但与此同时，大量的天线与射频链路不仅导致系统复杂度和成本的增加，还使得系统功耗不断增大.因此，相比于传统MIMO 系统，仅以最大化系统和速率或容量作为研究目标已无法满足系统性能需求，关于大规模MIMO 系统的能效研究显得尤为重要.如何获得最大的能量效率成为大规模MIMO 系统的分析和设计的核心任务之一，也是如今5G 大规模天线系统商用化亟需解决的问题.

针对大规模MIMO 系统的能效问题，学术界已有较多研究，主要可分为通过天线选择优化系统能效[2-6]、采用合理的功率分配方案优化系统能效[6-10]、通过权衡系统频率和能量效率优化系统能效[11-14]以及联合多维参数(如天线数、功率分配、用户数等)优化系统能效[15-18]四个方面.文献[2]研究了大规模MIMO 下行链路系统，推导了系统最大容量的闭合表达式，并通过仿真结果证明了通过天线选择提高系统能效的可行性；文献[3]采用迫零(zeroforce，ZF)预编码，根据大规模MIMO 系统能效下界，利用朗伯函数推导出使能效最佳的发射端天线数；文献[7]利用非线性规划理论和二分法对用户功率进行分配，从而提升了系统能效；文献[14]研究了大规模MIMO 系统在线性预编码下频效和能效的折中问题，提出了两种改进的粒子群算法，将多目标优化问题转化为单目标优化，在一定程度上提升了系统能效；文献[18]针对大规模MIMO 上行链路，在最大能效下，使用分式规划理论和拉格朗日对偶算法对发射端天线数、小区用户数以及功率分配进行优化.综上，在目前大规模MIMO 系统能效问题研究中，对于同时考虑天线、用户、功率三个参数对系统能效影响的研究，多针对系统天线数、用户数以及功率分配的影响，而联合天线选择与用户调度(joint antenna selection and user scheduling, JASUS)，并同时考虑功率分配的研究还较少.文献[19]研究了大规模MIMO 上行链路系统，以最大化系统能效为准则，采用ZF 接收技术，对基站端发射天线数、功率分配以及用户选择进行了联合优化，但并没有考虑基站端具体天线选择对系统能效的影响；文献[20]以最大化系统和速率为目标，利用信道矩阵的平方范数同时进行天线选择和用户调度，采用注水法对功率进行分配；文献[21]提出一种天线和用户的交替搜索方法，采用注水功率分配算法，实现系统和速率最大.文献[20-21]虽然考虑了天线选择、用户调度和功率分配三个方面，但二者的优化目标均为最大化系统和速率，而并未考虑对系统能效的影响；文献[22]以最大化系统能效为准则，提出了一种基于学习的随机梯度下降算法用于求解天线选择和用户调度问题，但并未考虑功率分配对系统能效的影响.

综上所述，合理的天线选择、用户调度以及功率分配均为提升系统能效的有效途径，针对现有关于大规模MIMO 系统能效的研究缺少对这三个方面的联合优化，本文以最大化系统能效为目标，综合考虑了天线选择、用户调度以及功率分配三个方面，通过对其进行联合优化，解决系统中天线选择和用户调度问题，从而提升大规模MIMO 系统的能源效率.本文将优化问题分解为两个子问题进行求解，首先在JASUS 时，提出一种低复杂度的双向交替搜索JASUS(bidirectional alternate search JASUS， BASJASUS)算法；其次利用分式规划理论[23-24]和拉格朗日对偶法来解决搜索过程中的用户功率分配问题，将三个参数进行迭代优化，从而达到系统能效最优.仿真结果表明，本文所提算法提升系统能量效率的同时，保证了算法的低复杂度.

1 系统模型

本文考虑一个单小区大规模MIMO 下行链路通信系统，如图1 所示.基站端配备有N根天线，M根可用射频链数，从N根天线中选出M根可用天线；信号在经过预编码和天线选择后，到达接收端；接收端有L个单天线用户，N≫L.假定该系统在某一时隙内有M根天线与用户通信，且仅有K个用户能够被调度.

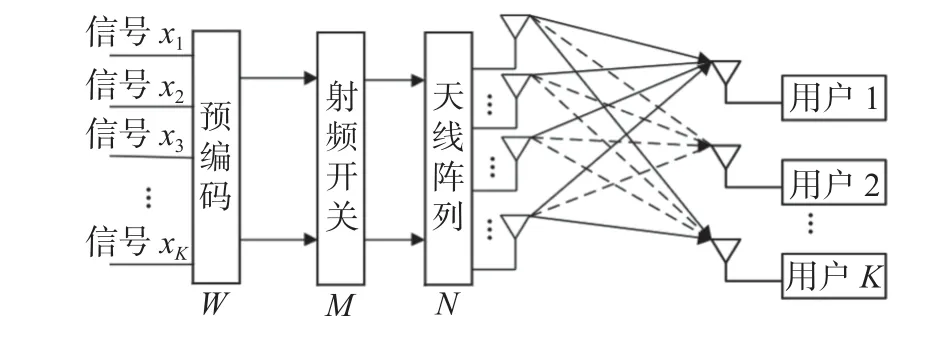
图1 单小区大规模MIMO 下行链路通信系统模型Fig.1 System model for single-cell massive MIMO downlink communication

在上述模型下，用户端接收到的信号可表示为[25]

式中：y为K个用户接收到的K×1信 号向量； ρ为基站发射功率；H为通信用户与选定天线间K×M的信道矩阵，hk为用户k在某一时隙内1×M的信道向量；W为M×K的预编码矩阵，为消除小区内不同用户间的干扰，本文选择采用ZF 预编码[26]，即W=HH(HHH)-1；x=[x,x,···，x]T为发射端12K发 出 的K×1信 号 向 量；n=[n1,n2,···nK]T为 服 从(0，1)分布的K×1高斯噪声向量.假设信道为服从独立同分布的瑞利平坦衰落信道，且信道响应在一定时间帧内保持不变，接收端第k个用户接收到的信号可表示为

式中，pk为基站分配给用户k的下行链路功率.用户k处的信干噪比(signal-to-interference-plus- noise，SINR)可表示为

式中，B为系统带宽.

定义系统总能效为系统传输总速率Rtotal与传输总功耗Ptotal的比值，即

本文考虑系统Ptotal由发射功率消耗和电路功率消耗两部分组成：

式中：Pc为 基站端每根天线消耗的电路功率； η为能量转换效率.则式(5)可具体写为

由于本文采用ZF 预编码，用户间干扰可被忽略，因此，可将式(8)简写为

由式(9)可知，系统能效主要与天线和用户以及每个用户的发射功率有关.

2 JASUS 的能效优化

本节以最大化系统能效为目标，对天线选择、用户调度和功率分配进行联合优化.首先，将能效优化问题拆解为JASUS 子问题以及功率分配子问题两部分；其次，针对天线选择和用户调度子问题，结合递增递减思想，以最大化系统能效为准则，提出一种双向交替搜索算法；最后，采用分式规划理论和拉格朗日对偶数学方法解决功率分配子问题.本节所提算法，不仅优化了系统能效，同时解决了在大规模MIMO 系统中，由于天线数和用户数量庞大使得选择天线和调度用户算法复杂度高且须同时兼顾算法性能的问题.

2.1 优化模型

本文的研究目标是通过优化选择天线集和用户集，以及用户功率分配使系统能效达到最大，因此，可将上述优化问题表述为

式中：p=[p1,p2,···,pk]为基站分配给每个用户的功率 集；Usel、Asel分 别 为 已 选 天 线 和 用 户 的 集 合；Uall、Aall分 别为所有天线和用户的集合；Pt为系统最大发射功率.

式(10)所描述的问题是一个组合优化问题，需要对天线集的选择、调度用户集的选择以及用户的功率分配三个变量进行求解.该问题可通过穷举法得到最优解，但具有非常高的复杂度，在实际应用中难以实现.因此，本文提出一种次优解法.根据优化模型的结构和其约束条件，将复杂的三变量优化问题分解为两个子优化问题，分别为：1)在确定的功率分配下，解决天线选择和用户调度的优化问题，如式(11)所示；2)在确定的天线集和用户集下，对用户进行功率分配，如式(12)所示.

需要说明的是，在每次用户集更新后，都须重新进行一次功率分配.

2.2 天线选择与用户调度子问题

在确定的功率分配下，针对JASUS 问题，本文基于递增递减思想，提出一种低复杂度的基于能效最大化的BAS-JASUS.

1)首先，固定用户集，进行天线选择.定义所选天线失活，即该天线在当前时隙内不发射信号时的系统能效为

式中，(x)-表示天线x失活.

使系统能效最大表明该天线能效贡献最低，因此从待选天线集Aall中将该天线删除；使系统能效最小表明该天线能效贡献最大，将该天线从待选天线集Aall中 删除并放入已选天线集Asel中，即：

2)固定天线集，进行用户选择.定义单个用户提供系统能效为

3)进行迭代，重复步骤1 和2，直到选够天线数与用户数，即：

具体算法步骤如表1 所示.

表1 BAS-JASUS 算法(算法1)Tab.1 BAS-JASUS algorithm(algorithm 1)

2.3 功率分配子问题

在给定天线集、用户集的情况下，可将问题表述为如下优化模型：

式(5)为分式形式，可通过分式规划理论进行简化求解.分式规划理论已广泛应用于现有大规模MIMO 各类优化问题求解中，在文献[23]智能超表面辅助无小区网络通信系统预编码设计最大化系统和速率中，采用多维复二次变换(multidimensional complex quadratic transform，MCQT)分式规划算法进行了子问题求解；在文献[24]智能超表面辅助无人机通信系统设计波束成形最大化系统和速率中，通过对分式形式的子问题泰勒级数展开进行求解.本文利用分式规划理论[27]，将分式转换为减式形式，即将目标函数(25)写为

目标函数(26)的拉格朗日函数可表示为

式中， λ ≥0，为拉格朗日乘子.其对偶问题可表示为

根据KKT 条件，给定 λ，最优功率分配p可表示为

因 为pk≥0 ， 所 以[x]+=max{0,x}.

运用梯度法[18]更新拉格朗日乘子 λ：

式中：t 为迭代次数； δ1为迭代步长.

具体算法步骤如表2 所示.

表2 功率分配算法(算法2)Tab.2 Power allocation algorithm(algorithm 2)

2.4 算法复杂度分析

在天线选择部分，我们首先使用式(13)计算删除任意天线时系统的能效，其计算复杂度为O(KM2)；然后根据式(14)～(15)比较所有情况，其复杂度为O(2M).因此，天线选择部分的整体复杂度为O(2M+KM2).在用户选择部分，我们首先使用式(18)计算每个用户的能效值，其计算复杂度为O(KM)；然后根据式(19)～(20)比较所有情况，其复杂度为O(2K)，并在迭代过程中根据算法2 进行功率分配，假设算法2 复杂度为O(T).因此，用户调度部分的整体复杂度为O(2K+KM+T).由于天线选择部分重复 (N-M)/2 次 ，用户调度部分重复 (L-K)/2次，所以算法整体复杂度为O((N-M)(2M+KM2)+(L-K)(2K+KM+T)).而此问题的最优解法穷举法计算复杂度为远大于本文算法复杂度.

3 仿真结果分析

本文仿真部分考虑单小区大规模MIMO 系统下行链路通信，基站端有N根天线和M根射频链路，且小区中有L个用户；假定从N根天线中选出M根天线，从L个用户中选出K个用户；初始功率使用平均功率分配算法，算法仿真参数如表3 所示，为比较算法性能，参数选取与文献[21]一致.

表3 仿真参数Tab.3 Simulation parameters

为了进一步验证算法性能，分别与随机天线用户选择、仅天线选择、SN-JASUS[20](squared normed based JASUS)、 JAUS-LCC[21](joint antenna and user selection with low computational complexity)算法进行比较.SN-JASUS 在进行天线选择与用户调度时，以最大化系统和速率为目标，基于范数对天线和用户进行选择；JAUS-LCC 以最大化系统和速率为目标，基于递增思想，对天线与用户进行交替联合搜索.在仿真过程中，对随机选择、仅天线选择与SN-JASUS三种算法采取平均功率分配，JAUS-LCC 采取与本文相同的功率分配方法.

图2 给出了本文算法与其他四种对比算法在不同天线数下的系统能效仿真结果.其中调度用户数K=20， 最大发射功率Pt=30 dBm.如图2 所示，系统能效随着天线数的增大逐渐减小.这是因为在调度用户数和最大发射功率固定的情况下，根据能效公式(9)，系统能效主要受位于分母位置上的天线数的影响.本文所提算法优于其他四种算法，对比随机选择算法和仅天线选择算法，本文算法考虑更加全面，不仅考虑了对天线的选择，还同时对用户进行了选择.对比SN-JASUS 与JAUS-LCC 算法，在天线选择和用户调度过程中，本文是以最大化系统能效为准则进行选取，而SN-JASUS 考虑的是用户信道间范数的影响且以最大化系统和速率为目标，JAUSLCC 也同样是以最大化系统和速率为目标，且由于仅基于递增思想对天线和用户进行选择，复杂度高于本文算法，由此二者算法性能均劣于本文所提算法.同时，随机选择算法和仅天线选择算法的性能劣于本文算法的结果能够证明，在大规模MIMO 系统中，尤其是在总天线数远大于选择天线数的情况下，进行合理的天线选择对提高大规模MIMO 系统能效有着重要作用，对天线选择的研究工作是有意义的.

图2 不同天线数M 下几种算法的能效对比Fig.2 Energy efficiency for different antenna number M

图3 给出了本文算法与其他四种对比算法在不同用户数下的系统能效仿真结果.其中基站端天线总数N=300， 选择天线数M=45， 发射功率Pt=30 dBm.如图3 所示，随着用户数的增大，系统能效也不断增大.这是因为根据能效公式(9)，在固定选择天线数和最大发射功率的情况下，系统能效主要受分子的影响，而分子值的大小随着用户数的增大而增大.其中，在用户数较小时，图中曲线较为接近.这是因为由式(9)可得，当用户数远小于天线数时，用户数对系统能效影响远小于分母中天线数对的影响，所以各类算法所得仿真结果相近.从图3 仿真结果可以得出，本文算法性能优于其余种算法，这是因为本文算法所选用户为在当前时隙内具有最优能效.而且考虑到了对用户的功率分配，即信道质量较好的用户分配较高功率，信道质量较差的用户分配低功率，从而合理分配系统资源，且使系统能效进一步提升.同时，仿真结果表明，在大规模MIMO 系统中，某一固定的时隙内对用户进行合理调度，选取信道质量好的用户进行通信能够提升系统能效.

图3 不同用户数K 下几种算法的能效对比Fig.3 Energy efficiency based on different algorithm for different user number K

图4 给出了本文算法与其他四种算法在不同发射功率下的系统能效仿真结果.其中，基站端天线总数N=100， 选择天线数M=30， 调度用户数K=20.如图4 所示，SN-JASUS、随机选择与仅天线选择算法的能效值随着发射功率的增大先增大后减小.这是因为三种对比算法采取的是平均功率分配策略，根据能效公式(9)，在用户和天线固定的情况下，能效是关于发射功率的凸函数，因此存在使能效能够达到最优值的最大发射功率.而本文算法与JAUS-LCC算法曲线走势为先上升后基本趋于平稳.此外，本文算法能效值始终大于四种对比算法.这是因为四种对比算法采取的平均功率分配策略，并未进行优化；而本文算法采用了拉格朗日对偶算法以能效最大化为目标对功率分配进行了优化，为信道质量好的用户分配大功率，信道质量较差的用户分配小功率.由图4 还可看出，JAUS-LCC 虽然也对功率分配进行了优化，但其在发射功率较小时，性能较差.仿真结果证明，在大规模MIMO 系统中，选取合理的发射功率，并对用户进行功率分配，能够实现优化系统能效的目标.

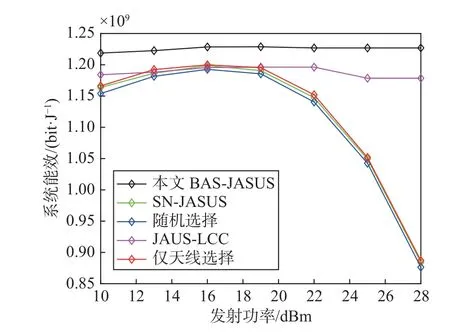
图4 不同发射功率 Pt下几种算法的能效对比Fig.4 Energy efficiency based on different algorithms for different transmission power Pt

图5 给出了调度用户数K=20、选择天线数M=30、 最大发射功率Pt=16 dBm时，系统能效随本文算法迭代次数的变化.可以看出，在较少的迭代次数情况下，本文算法能够实现最大化系统的能效.

图5 本文算法中不同迭代次数下的系统能效Fig.5 Energy efficiency under different iterations with the proposed algorithm

4 结 论

本文针对大规模MIMO 系统的能效问题，考虑大规模MIMO 下行链路，采用ZF 预编码消除用户间干扰，以系统能效最大为准则，对系统天线集的选择、用户调度以及功率分配进行联合优化研究，提出BAS-JASUS 算法.仿真结果表明，与传统算法相比，本文算法在JASUS 时，具有较好的性能且较低的复杂度；并能够有效提升系统能效，合理利用系统资源，适合应用在大规模MIMO 系统中.