基于散射中心模型的目标电磁特性智能生成网络研究

孙圣凯 何姿* 管灵 董纯柱 樊振宏 丁大志 殷红成

（1.南京理工大学电子工程与光电技术学院, 南京 210094；2.北京环境特性研究所, 北京100854）

0 引 言

雷达通过电磁波的发射与接收来探测目标的电磁特性，具有全时段、探测距离远、目标识别能力强等优点，已经成为国防安全领域必不可少的工具.随着无线通信技术的不断提升，高分辨雷达探测技术也得到飞速的发展.无论是在目标侦察、区域警戒、定点打击等军事领域还是矿物探测、气象预报、天文观测等民用领域都具有重要应用前景.针对工作于高频区的雷达，目标总的散射场可以由某些局部位置的散射场叠加而成，通常将这些局部的散射源称为散射中心[1].散射中心不仅能提供该局部散射源的幅度、位置、极化、结构等信息，而且能简洁、完备地描述目标总的散射场，进而根据散射中心模型中的信息参量完成目标散射场的重构.因此，散射中心对于目标电磁散射特性研究至关重要，在目标识别[2]、数据压缩与融合[3]以及雷达散射截面积(radar cross section，RCS)的外推[4]等方向都扮演着重要角色.

20 世纪60 年代便已经开展了散射中心模型的研究.早期目标被近似为一个点目标，即理想点模型.随着雷达技术的不断发展，理想点模型已不能准确表达雷达目标的频率依赖性.1987 年，Hurst M P 等[5]发现电场幅度对频率具有依赖关系，并提出了Prony模 型.1995 年Potter L C 等[6]从 几 何 绕 射 理 论(geometrical theory of diffraction, GTD)入手，提出了用幂函数 (jk)α来表示不同类型的散射中心对频率依赖性的GTD 模型.2004 年，Rigling B D 等[7]研究了有关球、平板、高帽、二面体、三面体间二次耦合时的频率依赖因子.2018 年，闫华等通过物理光学法和几何光学法对各种散射类型间二次耦合时频率依赖因子的取值给出了明确的补充，并于2021 年采用驻留相位法进一步得出各散射类型间任意多次耦合所形成的频率依赖因子[8].以上文献中的GTD 模型强调了散射点幅度对频率变化的依赖关系，但并没有考虑方位变化对幅度的影响.1999 年Gerry M J 等[9]在GTD 模型的基础上，分别用 sinc 函数和指数函数描述局部式和分布式散射中心幅度对雷达入射方位角的依赖关系，提出了属性散射中心模型.2010 年Jackson J A[10]研究发现，双站下的分布型散射中心的幅度衰减满足sinc 函数.郭琨毅等[11]、赵晓彤等[12]也陆续给出了多种模型的角度依赖函数.除此之外，对于复杂模型的散射中心研究也在不断进行.2011 年，马梁等[13]针对弹头的微动特征给出了位置随观测角改变的滑动散射中心模型表达式.2019 年李奇峰等[14]给出了矩形深腔中经多次反射产生的等效散射中心位置.2021 年袁文杰等[15]利用目标表面电流的相位信息，给出了流线型目标上滑动散射中心的位置.因此，选取合理的散射中心模型是确定散射中心与散射场之间联系的关键.

2014 年，何洋等[16]提出基于几何光学和物理光学的弹跳射线法(shooting and bouncing ray, SBR)的射线分集技术，对目标散射中心进行提取.SBR 方法是目前最流行的高频方法之一，具有计算速度快、计算量小的特点.如何利用基于SBR 的散射中心提取方法在计算效率的优势，并减小散射中心模型描述所带来的误差，提升其回波重构精度是本文所要解决的问题.

近年来，机器学习的飞速发展，为各项研究开辟了更为广泛的研究方式.其中，反向传播(back propagation, BP)神经网络通过学习数据库中的已有信息，修正数据间的权值，实现训练值和真实值的误差极小化，进而有效地对该信息系统进行分析和预测.2019 年Jiang J 等[17]利用BP 网络实现了逆散射成像，Zhu L 等[18]通过BP 网络对地面目标实现了精确分类.2021 年，Zhou T 等[19]采取BP 网络提高了微波成像质量，Xu L 等[20]将BP 网络用到了光学图像偏差的预测.2022 年，Tian J 等[21]采用BP 网络实现了快速准确的大气参数反演.可见，BP 网络凭借其强大的非线性拟合能力、非线性映射能力以及突出的自学习自适应能力使得其在工业工程、学科交叉、复杂问题优化预测等领域得到了迅速的推广及应用，但有关神经网络结合散射中心模型的应用研究目前较少.将散射中心应用于神经网络的目标散射特性预测中[22]，能够更清晰地解释网络各参量的物理意义.同时，根据各自参量的实际意义进行网络架构，使得网络具有更强的泛化能力.

本文提出了一种新型并联智能生成网络，实现了基于散射中心的全角度、宽频带目标电场有效预测.首先，通过基于SBR 的散射中心正向获取技术来获得目标某姿态及频率下的散射中心信息[23]，并以此作为网络的输入参量，将采用高频算法得到的复电场作为网络输出参量，进而实现网络的训练.其次，考虑到针对目标全角度、大带宽的预测，构造了并联智能网络结构，对数据进行筛选判断，选择最优分支网络进行预测.以此来解决不同角度下散射中心个数不同导致的网络输入层节点变化的问题.同时，对于频率的划分将缓解散射中心频率依赖的影响，提高电场预测精度.当网络充分训练后，能够实现目标由位置、强度、频率等数据相对应的目标远场电场的预测.最后，利用该网络代替传统的散射中心模型，不仅能降低电场计算复杂度，还能减小散射中心模型频率和角度的依赖性带来的影响，提高目标远场电场预测的精度.数值算例表明，该方法具有良好的电场预测效果.

1 基于SBR 的正向参数化获取技术

SBR[24]主要分为两个过程：射线路径追踪以及射线管远场积分.采用平行射线照射目标，射线将会在空间中沿直线传播，当与目标表面产生接触时发生反射，传播路径随之改变.通过对一系列的离散三角形追踪，得到射线完整的传播路径，对每条射线进行远场积分计算该射线携带能量.将处于同一射线子集中的射线能量累加得到目标某个子部件或者若干子部件耦合所产生的散射源为

式中：E(S j) 是 整个子集S j的总能量，表示某一部件的散射强度；E(km)是 每条射线km携带的能量.

在射线追踪过程中，若某一子集内只有一条射线，则认为其所对应部件的散射中心位置位于射线在其表面发生反射处.若某一子集内含有多条射线，则需要根据射线子集中的所有射线的强度对其反射位置进行加权平均.散射中心位置受所有射线的影响，其位置表示如下：

式中： (xn,yn,zn)是 射线kn在目标表面产生反射时的坐标；wn是 由射线kn按其能量所产生的权重.

获得散射中心三维位置参量后，利用投影矩阵计算其在距离向与方位向上的投影即可获得散射中心在距离向和方位向上的位置.投影矩阵表示如下：

式中：u，v分别表示散射中心在二维面上的距离向与方位向位置信息； θ，φ分别表示雷达的俯仰角和方位角.

2 基于BP 网络的智能网络构建

在实际应用场景中，雷达所面对的目标不仅仅是各种基于平面、曲面反射，边缘、角绕射所产生的散射效应.随着隐身技术的发展，行波、爬行波等也受到越来越多的关注.而现阶段所熟知的散射中心模型对于频率和角度的依赖项的研究并不涉及上述散射机理.目前对各种复杂散射机理的研究工作也在不断进行，但并没有对其后向散射的等效散射中心给出明确的数学模型.因此建立一种实现散射中心与目标电场之间稳定联系的途径十分必要，这里将利用BP 神经网络基于散射中心参数对目标电场的实部与虚部进行快速获取.

BP 神经网络是目前在各个领域应用最为广泛的一种神经网络，凭借强大的非线性映射以及自学习、自适应能力，在实际工程的众多领域取得了良好的表现.基于以下考虑选取BP 网络进行电场预测：

1) BP 网络在各领域实际工作中充分体现了其对非线性问题具有很强的解决能力，并且面对不同的问题，其网络结构易于调整，能够按照需要做出不同设计.

2) BP 并行网络结构相互独立，互不关联.针对模型的全角度、宽频带问题，能够将其按照不同的区间单独训练，这种性质使得其在面对复杂模型时，同样能够取得不错的效果.

3)BP 网络的训练学习方式是利用损失函数计算每次传播损失，并将其反向传播给网络.现阶段的研究已经证明了散射中心与电场之间必然存在某种数学形式的联系，而BP 网络的这种不间断学习过程，最终能够实现从散射中心到目标电场的准确预测.

BP 神经网络是一种多层前馈型网络，网络结构图如图1 所示.它包含一个输入层、多个隐藏层和一个输出层.输入量为频率f、散射中心位置信息(x,y) 、散射中心强度信息A等雷达参数和散射中心参数，输出为目标电场实部Er和电场虚部Ei.

图1 BP 网络结构图Fig.1 Structure of BP

利用散射中心进行目标电场重构的传统方法，是根据散射中心模型通过对各个散射中心的累积获得目标总电场.以GTD 模型为例，其表达式如下：

可以看出，目标电场E与 强度A、 位置 (x,y)以及频率依赖因子 α有关.考虑到频率依赖项 α无法反映所有的散射机理，故在网络训练过程中采用散射中心强度A和 位置 (x,y)来表征目标散射特性.通过借鉴现有模型中各散射参数对目标电场的影响，能够使预测网络输入、输出数据具有一定物理意义.另外，网络数据的选取能够较全面地反应电场变化的影响因素.

BP 网络通过良好的训练，可以替代散射中心模型，该过程将不再受模型的制约.电场预测过程可以分为网络离线训练和在线预测.离线训练过程包括前向传播和后向传播两个阶段.其中前向传播是根据当前网络的权值计算输出电场和实际电场之间的损失；后向传播是基于该损失使用梯度下降法不断更新权值.

前向传播过程即目标电场预测的过程，表达式为：

式中： [x1,···,xp,y1,···,yp,A1,···,Ap,f]表示输入的散射中心参数和频率；[Er,Ei]表示输出的目标特定姿态下的电场实虚部；S(i)表示经过i层激活函数后的计算结果；W(i-1)、b(i-1)、s分别表示第i-1层的权值、偏置以及非线性激活函数.这里采用Relu 函数作为激活函数.

利用当前网络权值计算的输出电场和采用精确数值方法得到的电场来定义均方差(mean square error, MSE)作为损失函数：

式中：m表 示测试数据个数；E1表示在网络当前的权值、偏置下输出的电场，E1=Er+iEi；E2表示采用高频方法得到的复电场.

式中：M(N)表 示网络输出层的误差； ◦表示哈达玛积；s′表 示对激活函数求导；M(i)表示第i层的误差.最终计算出权值和偏置的更新形式为：

式中， η ∈(0,1)表示学习速率.

3 基于散射中心模型的并联智能网络生成技术

基于散射中心模型的并联智能网络结构如图2所示.为了实现网络对目标的全角度、宽频带的在线远场电场预测，将会在大带宽、广视角下对网络进行训练.但由于网络输入层节点个数不同、散射中心具有频率依赖性等因素，可能会导致网络在电场预测过程中结构设计困难，预测误差大.因此考虑通过神经网络的并联思想，将宽频带适当分为若干个子频带，全角度经二维角域划分为若干个子角域.将这些子频带跟子角域合理搭配，实现对目标的全角度、宽频带下远场电场估计.在离线训练过程中，宽频带可以根据输入的频率信息作为子网络特征选择信息；全角度的处理过程要借助其散射中心个数，判断其所对应的子角域.并联智能网络结构相互独立，互不关联.将样本库按照不同的区间单独训练，形成多个子网络，每个网络的权值、偏置将满足该区域下的散射中心参数到远场电场的映射.采用并联智能网络离线训练，一方面解决了网络输入层个数不一致的问题，使网络能够有效实现电场预测；另一方面，对于每个子网络筛选出该区域下的强相关信息，避免其他区域下样本的干扰，减小散射中心频率依赖性的影响，使得网络训练更易收敛，降低误差.

图2 全角度、宽频带电场预测并联智能网络Fig.2 Full angle, broadband electric field prediction parallel intelligent network

在针对目标远场电场在线预测时，散射中心参数以及雷达参数输入网络根据目标子域划分准则，对其所属区域进行判断，将输入参量传递到不同的子网络.并联子网络彼此之间相互独立，所有子集的集合将能够覆盖目标所须估计的角度范围以及频域范围.通过并联智能生成网络的各层之间的权值、偏置完成对目标远场电场的在线预测，并输出预测电场信息.

4 数值仿真和分析

RCS 定义为

式中，E为复电场.

均方根误差(root mean square error, RMSE)定义为

式中：E1为 重构或预测电场；E2为高频方法计算得到的电场.

相对均方根误差(relative root mean square error,RRMSE)定义为

误差减小比(error reduction ratio, ERR)定义为

式中， e rror1， error2分别为两种对比方法的误差.

网络训练参数如表1 所示，网络训练过程是一个更新网络权值与偏置的过程，旨在确定网络输入的散射中心参数与输出电场之间的最佳权值与偏置.将训练得到的权值与偏置加载入网络后，可以通过散射中心参数直接计算目标电场，因此能够将该网络看作为一个等效的散射中心模型.

表1 网络训练参数Tab.1 Network training parameters

算例1 如图3 所示，对于一个底面半径r=0.5 m 、高h=1 m的圆锥，考虑到其旋转对称性，在θ=0°～30°方向上间隔 0.6°扫角，获取3 个散射中心，频率范围为3～5 GHz，扫频间隔为40 MHz.共有2 601 组数据集，随机选取其中200 组数据作为测试集.

图3 圆锥模型Fig.3 Cone model

经并联智能生成网络预测和通过GTD 模型重构得到的结果对比如图4 所示，表2 给出了200 组随机数据下两种方法获得电场和RCS 的RRMSE.可以看出，本文方法对远场电场的预测结果较基于GTD 模型重构的电场实虚部RMSE 分别下降了60.1%、87.7%，RCS 误差下降了71.3%.

表2 本文方法预测电场与GTD 模型重构电场RMSE 和RRMSE 对比Tab.2 Comparison of electric field prediction of RMSE and RRMSE using proposed method and GTD model reconstruction

图4 电场预测/重构结果Fig.4 Electric field prediction / reconstruction results

通过以上结果不难发现，本文方法对远场电场的预测值十分接近高频方法的远场电场，实虚部RMSE 和RRMSE 分别为0.000 857、0.000 219 以及2.3%、6.08%.并且该方法对电场的预测精度要明显高于GTD 模型重构结果，电场虚部尤为明显，其ERR 达到87.7%.表明所提方法在依据散射中心参数预测目标电场方面有着不错的效果，为电场重构过程中减小散射中心模型带来的误差提供了新思路.

算例2 建立一个如图5 所示的组合模型，其参数见表3.为了验证并联网络的优势，本算例将对传统BP 网络及并联BP 网络对于电场的预测性能进行对比.选定两个子角域，其中角域1 为{θ∈(60°，72°)，φ∈(-30°，-18°)}，角域2 为{θ∈(72°，84°)，φ∈(-18°，-6°)}，该 角 域 内 提 取 模 型 的17 个 散 射 中 心.传 统BP 网络将对两个角域数据集同时训练，而并联BP 网络将对两个区域数据分别训练，测试数据为角域1 中的散射中心和电场信息.网络的训练损失值如图6 所示，随着训练轮数的增加，损失值收敛.同时，表4 给出了测试数据的RMSE 和RRMSE，图7给出了两种网络结果的对比.可以看出，采用并联结构后，网络对于组合体远场电场实虚部预测的误差分别下降了17.9%、43.2%，RCS 误差下降了19.8%.

表3 组合体模型参数Tab.3 Combination model parameters m

表4 不同角域下两种网络结构预测电场的RMSE 和RRMSE 对比Tab.4 Comparison of electric field prediction result of RMSE and RRMSE under two network structures in different angle domain

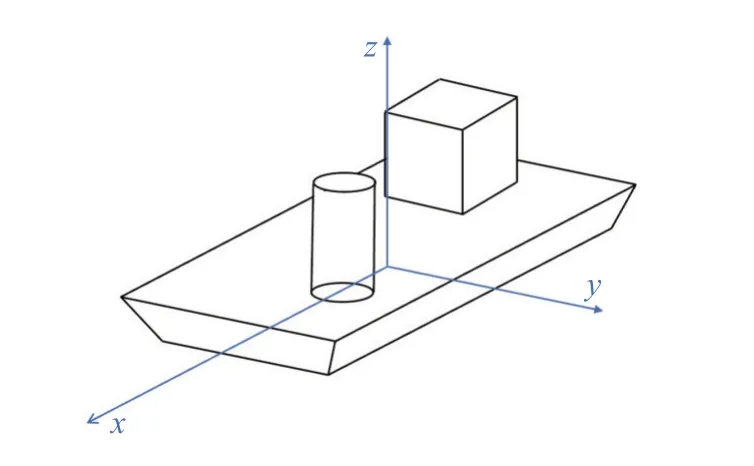
图5 组合模型Fig.5 Composite model

图6 两种网络结构训练误差Fig.6 Training error of network

图7 电场预测结果Fig.7 Electric field prediction results

考虑到宽频带的预测，在角域3{θ∈(60°，72°)，φ∈(0°，12°)}内，取 频 域1 为2～3 GHz，频 域2 为4～5 GHz.同样，传统BP 网络将两个频域的数据集同时训练，而并联网络将对两部分频域信息分别训练，最后获得频域1 内的电场预测信息.表5 对比了测试数据的RMSE 和RRMSE.可以看出，对于目标宽频带的远场电场预测，采用并联结构后网络预测误差同样下降20%以上.

由两种网络结构的电场预测结果可以看出，对于大带宽、全角度目标电场的预测，采用并联网络结构能显著降低电场预测误差，其误差能够降低17.9%以上.这对实现高精度远场电场预测十分有帮助.

算例3 建立一个如图8 所示长度为1.5 m 的导弹模型.随着雷达照射目标角度的变化，目标散射中心个数随之改变.角域1 中，散射中心个数N=1.角域2、3 中的散射中心个数分别为4 和2，导致网络输入层节点发生变化.因此，考虑根据不同角度下散射中心个数作为子角域划分的依据.由于模型具有旋转对称性，故其共被划分为3 个角域.表6 给出了每个角域中心角度处的散射中心位置信息.

表6 各角域中心角度处的散射中心位置信息Tab.6 Scattering center position information at the central angle of each angular domain

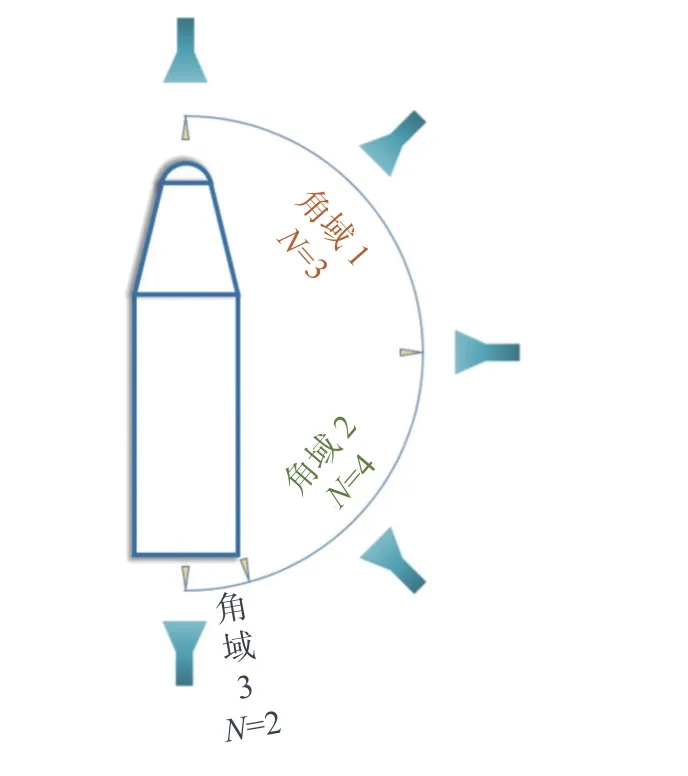
图8 导弹模型Fig.8 Missile model

散射中心具有频率依赖性，在散射中心模型中体现为 (jf/f0)αi.为使不同频段的散射中心在网络训练中尽可能处于一个相对均衡的状态，划分标准为

式中：f止与f始分别表示频段的终止频率与起始频率；k为一个常数，本算例中，取k=1.5.频率范围为2～4.5 GHz，则模型共被划分为2 个子频域，如图9 所示.

图9 模型频域划分Fig.9 Frequency domain classification of missile model

按照上述划分准则，该模型共有6 个子域，记子域12 为角域1 和频域2 搭配的子集.在带宽2～4.5 GHz，θ=0°～180°，φ=0°内，进行电场预测.扫频间隔为40 MHz，共 有63 个 扫 频 点，θ 的 扫 角 间 隔 均 为0.3°，共有37 863 组数据集.随机选取每个子域10%数据作为测试集，其余数据作为训练集.

选取子域11 和子域21 分别预测θ=90°时2～3 GHz 的电场信息，以探究相邻角域间的电场连续性；选取子域11 和子域12 分别预测3 GHz 下目标0°∼90°的电场信息，以探究相邻子频域间电场预测的连续性.其结果如图10 所示，表7 和表8 给出了各个子域中电场预测的RRMSE.

表7 各子域电场实部RRMSETab.7 RRMSE of electric field real part %

表8 各子域电场虚部RRMSETab.8 RRMSE of electric field imaginary part %

图10 子域连续性分析Fig.10 Continuity analysis of subdomains

对于导弹模型的大带宽、广角度电场预测结果显示，在所提出的子域划分准则下，并联智能生成网络预测电场的RRMSE 小于5%，说明本文采用并联BP 神经网络基于散射中心参数化模型对目标电场的实部与虚部进行快速预测是切实可行的，能够得到具有实际参考价值的远场电场信息，为针对目标的电场快速获取提供了参考.

5 结 论

本文基于散射中心参数化模型和BP 神经网络，构建了一种针对目标全角度、宽频段下的新型并联网络.该方法首先通过SBR 的散射中心获取技术对散射中心参数化模型各参量快速获取，然后利用BP 网络强大的映射能力建立散射中心参数化模型与高精度远场电场间的对应.网络采用并联结构，将整个频域以及角域按照所提出的准则划分为若干区间，每个区域的并联智能子网络相互独立.该方法对于电场的预测不再依靠传统的散射中心模型，避免了散射中心模型自身局限所产生的误差，与传统基于模型的电场重构方法相比，该方法能够更准确高效地实现目标远场电场预测.通过对几种模型的远场电场预测发现，该方法对于电场预测的RRMSE小于5%.