常法向刚度条件下人工结构面剪切力学特性及损伤演化规律试验研究

焦 峰 ， 许 江 ， 彭守建 ， 何美鑫 ， 张心睿 ， 程 亮

(重庆大学 煤矿灾害动力学与控制国家重点实验室, 重庆 400044)

针对于浅部和深部工程，岩体中都存在大量的弱面，如结构面等，同时结构面容易受到压剪破坏。随着浅部资源的不断开发，逐渐呈现出枯竭的趋势，因此陆续向深部能源开采进发[1-3]。由于深部工程灾害频发且不同于浅部灾害[4]，因此解决深地工程面临的问题具有迫切性。浅部岩体不考虑剪胀效应，对法向荷载的影响属于常法向应力边界条件(CNL)，而深部岩体由于围岩的限制而不能自由剪胀，因此作用在岩体上的法向荷载会持续增加，属于常法向刚度(CNS)边界条件。CNL 条件容易实现，且取得了丰硕的成果，张丹等[5]开展了不同法向应力条件下具有二级凸起体结构面的直剪试验，分析了结构面的剪切破坏模式，验证了二级凸起体破坏的方式。卢海峰等[6]通过开展不同法向应力下注浆结构面的直剪试验，分析了注浆条件对结构面形貌特征的影响。祝艳波等[7]利用结构面直剪试验，探究粗糙度对剪切力学性质的影响。贾云中等[8]通过变滑移速率下页岩结构面剪切试验，基于摩擦因数和渗透率变化分析了渗透性响应特征及演化规律。MORAD D 等[9]通过粗糙石灰岩结构面的剪切试验，研究了剪切速度对结构面剪切力学性质的影响。江权等[10]鉴于3D 打印技术可以便捷地制作含复杂结构的三维实体，将3DP 技术引入到岩体/岩石力学试验研究中。芦谭等[11]通过三维扫描和3D 打印技术，利用光敏树脂材料制作结构面模型，通过直剪试验验证了技术的可行性，为之后的研究方法提供了参考。随着光学技术的进步，使得结构面的形貌数据更加精确，因此对结构面强度模型的研究同样取得了大量的研究成果[12-16]。但是CNS 条件更加符合工程背景，近年来，随着试验设备性能的不断提高[17-20]，CNS 条件的研究成果有所增加。赵衡等[21]通过做CNS 条件下的岩石-混凝土结构面的直剪试验，给出了结构面粗糙度的度量方法，推广了Patton 模型。尹乾等[22]通过做CNL 和CNS 条件下的直剪试验，揭示了初始法向应力对砂岩剪切力学参数的影响。蒋宇静等[23]通过开展CNS 条件下锚固和非锚固类岩石节理的剪切试验，研究了边界条件对节理力学性质的影响。刘日成等[24]通过开展CNS 条件下具有三维粗糙度结构面的直剪试验，揭示了法向刚度和循环剪切次数对剪切力学性质的影响。HAN 等[25]通过做CNS条件下不同类型结构面的直剪试验，探究了结构面的剪切力学性质。GUTIERREZ-Ch 等[26]进行不同边界条件下岩石-混凝土界面的直剪试验研究，并通过数值模拟结果对他人的研究成果进行验证。

但是以上研究没有将法向刚度的作用机理与结构面的破坏模式联系起来。因此，笔者在充分考虑剪切位移的基础上，系统探究了起伏角和法向刚度对结构面剪切力学特性的影响，得到CNS 条件下结构面的剪切力学特性及破坏模式，同时分析剪切过程中结构面的动态破坏过程。

1 试 验

1.1 试样制备

由于剪切试验会使结构面产生不可逆的破坏，同时天然结构面不具有重复性，因此笔者使用自主设计的规则锯齿状结构面浇筑模具进行结构面制作，如图1 所示。此模具的主要优点是可以一次分别成型10 个具有起伏角α=15°、30°和45°起伏角的结构面，大大降低了结构面之间的差异性，使得试验结果更具有可靠性。模具主要由凸模底座、长隔板、短隔板、固定器和夹紧螺钉组成，具有可拆卸性。结构面为50 mm×50 mm×50 mm 的立方体试件，结构面上均匀分布10 个等腰三角形锯齿，底边边长为5 mm。结构面浇筑过程如图2 所示。步骤为：① 将砂粒在烘箱中以105 ℃烘干24 h；② 将砂粒和水泥进行筛分，保证颗粒均匀；③ 将水泥∶砂粒∶水=3∶2∶1.5 的质量比进行称重选取；④ 先将水泥和砂进行混合，在搅拌均匀之后加入水充分搅拌；⑤ 将水泥砂浆材料倒入到模具中，采用分层捣实的方法进行浇筑；⑥ 浇筑完成后，使用振动台进一步将结构面试件内部的气泡排出，静置成型2～3 d；⑦ 脱模，将试样放到养护箱中养护28 d，则结构面一次制作完成。结构面的基本力学参数，见表1。

表1 基本力学参数Table 1 Mechanical parameters

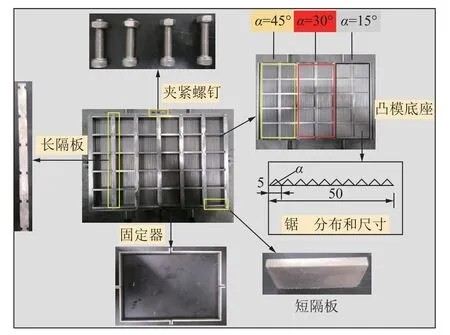
图1 结构面制作模具Fig.1 Mold making of structural plane

图2 结构面制作步骤Fig.2 Making steps of structural plane

1.2 试验装置

本文试验在自主研发的煤岩剪切-渗流耦合试验系统上完成[27]，该试验系统主要由伺服加载控制系统、剪切盒及其密封系统、数据采集系统和结构面三维形貌扫描系统组成，如图3 所示。该系统可以实现恒法向力(应力)、恒定变形(应变)、恒定位移、保载时间、应力路径多级加载等多种控制方式；其中三维扫描系统精度最高可以达到0.01 mm。使用试验机自带的复合控制方式可以实现CNS 条件的剪切试验[28]，具体步骤如下：① 轴向压头首先设置到99.8 mm，当压头到达指定位置时，转到步骤②；② 设置轴向压头以0.5 mm/min(接近速度)接近剪切盒上压头，当轴向压头力在接触后大于0.1 kN 时转到步骤③；③ 轴向转为力控制，以0.1 kN/s 的速度(预加载速度)，达到akN(初始法向力)，此时法向位移清零，转到步骤④；④ 轴向变为复合控制F=a+bx，其中，F为轴向力；a为初始轴向力；b为法向刚度系数；x为法向位移增量，直至试验结束。说明：常法向刚度的实现是通过数据采集系统实时监测反馈的结构面法向位移信息，根据设定的表征法向刚度的系数b，实时自动计算并调整法向应力。计算公式[29-30]为

图3 试验系统Fig.3 Test system

式中，Δσn为法向应力变化量，MPa；kn为法向刚度，GPa/m；Δδn为法向位移变化量，mm；t为时间，s；Δt为时间变化量，s。

1.3 试验方案

笔者主要研究起伏角和法向刚度对结构面剪切力学特性的影响，因此设置初始法向应力为1.5 MPa，法向刚度分别为0、1、2 和4 GPa/m[31-32]，其中法向刚度0 GPa/m 为对照组；设置起伏角为15°、30°和45°，每个条件进行2 次重复试验，共需结构面36 个。试验步骤为：① 轴向以0.1 kN/s 速度增加到初始法向应力；② 使用复合控制条件设置法向刚度值；③ 切向以1 mm/min 的速度施加剪切位移至25 mm，试验结束。考虑到剪切位移影响是不可忽略的[33]，所以设计剪切位移占剪切方向结构面长度的50%，充分考虑了剪切位移对结构面力学性质的影响。

2 试验结果

2.1 剪应力演化

结构面剪切应力-剪切位移曲线，如图4 所示。

图4 剪切应力-剪切位移曲线Fig.4 Shear stress vs shear displacement curves

由图4 可以看出，不同起伏角结构面的剪切应力-剪切位移曲线在峰前阶段演化基本相同，都没有明显的压缩阶段，表现为从剪切开始以弹性阶段增加到峰值强度，具体区别体现在峰后阶段。当结构面起伏角为15°时，剪切应力-剪切位移曲线在峰后呈现出周期型震荡衰减，即剪应力达到峰值后迅速降低至本周期最低值，然后随着剪切位移的增加，剪切应力再次达到峰值，在此之后随着剪切位移的增加，剪切应力同样以这样的规律进行演化，主要不同为每个周期内的峰值应力逐渐减小。到剪切结束时，随着法向刚度的增加，峰值剪切应力的降低量分别是1.78、1.42、1.36 和1.27 MPa，呈逐渐降低的变化趋势。特别是当kn=0 时，因为结构面在法向没有约束，所以峰值剪切应力的降低值最大。

当结构面起伏角为30°时，剪切应力达到峰值后，迅速降低至最小值，之后同样呈现出周期型震荡衰减的变化趋势。相较于起伏角15°结构面，主要区别在于剪切应力在峰后阶段的变化幅度较小，并随着剪切位移的增加逐渐达到残余强度。

当结构面起伏角为45°时，剪切应力达到峰值后迅速降低，在低法向刚度条件下，剪切应力在峰后逐渐减小；当kn=4 GPa/m 时，到剪切结束时，剪切应力基本不再发生变化。表明随着法向刚度的增加，结构面的破坏程度逐渐增加，在较小法向刚度条件下，结构面在剪切过程中的破坏相对较小，随着剪切位移的增加，结构面上仍有承担抵抗剪切的明显凸起体，因此随着破坏程度的增加，剪切应力逐渐降低。当法向刚度增加到4 GPa/m 时，发生切齿破坏，结构面上的凸起体几乎被剪断，达到残余强度。

不同起伏角结构面的峰值剪切应力随法向刚度的演化，如图5(a)所示。由图5(a)可以看出，随着法向刚度的增加，起伏角15°和45°结构面的峰值剪切应力呈现出线性增加的变化趋势，拟合优度R2分别为0.86 和0.98。起伏角30°结构面的峰值剪切应力与法向刚度没有明显的线性关系，呈现出分段函数的特征。当法向刚度从0 增加到1 GPa/m 时，峰值剪切应力迅速增加，之后几乎稳定不变。

图5 力学参数演化Fig.5 Evolution of mechanical parameters

详细原因是，当起伏角为15°和45°时，结构面主要发生磨损破坏和切齿破坏，破坏模式单一，并且随着法向刚度的增加，破坏模式不会发生变化，只是破坏程度逐渐增加，因此对应法向位移的变化量增加。结合式(1)和(2)可知，法向应力也会相应增加，对应CNL 条件下法向应力的作用机制，因此峰值法向应力线性增加。当起伏角为30°时，结构面的破坏模式较为复杂，即当法向刚度为0 时，由于凸起体高度较大，结构面发生爬坡破坏；当法向刚度为1 GPa/m 时，因为法向刚度增加，所以对应的法向应力增加，结构面发生全切齿破坏，因此峰值剪切应力增加，并且增加量要大于起伏角15°和45°结构面。接下来随着法向刚度的增加，结构面同样发生全切齿破坏，由式(1)和(2)可知，因为法向位移不再发生变化，所以对应的法向应力也不变，因此峰值剪切应力几乎没有变化，呈现出分段函数的演化特征。因此法向刚度是通过控制结构面的破坏模式来影响峰值剪切应力的。

使用剪切刚度来区分结构面在峰前演化的差异性。将剪切刚度定义为剪切应力-剪切位移曲线弹性阶段的应力梯度，表达式为

式中，kg为剪切刚度，GPa/m；τ为剪切应力，MPa；un为剪切位移，mm。

不同起伏角结构面的剪切刚度随法向刚度的演化，如图5(b)所示。

由图5(b)可以看出，随着起伏角的增加，剪切刚度逐渐增加，并且起伏角15°到30°结构面的剪切刚度增加量要大于起伏角30°到45°。表明当起伏角为15°时，因为结构面上凸起体高度较小，所以上下结构面之间的互锁效应较小[34]，抵抗剪切的能力较小，因此对应剪切刚度较低。当结构面起伏角为45°时，由于凸起体高度较大，上下结构面之间的互锁效应较大，抵抗剪切的能力较大，因此对应的剪切刚度较大。当结构面起伏角为30°时，结合峰值剪切应力演化规律可知，其对试验条件的依赖性较强，结构面发生的破坏模式较为复杂，因此剪切刚度值处于中间，更偏向于切齿破坏，所以在数值上接近于起伏角45°结构面的剪切刚度。

2.2 峰值法向应力演化

通过式(2)可知，CNS 条件下结构面在剪切过程中的法向应力不是一个定值。不同起伏角结构面的峰值法向应力演化，如图5(c)所示。

由图5(c)可以看出，当起伏角为15°和45°时，随着法向刚度的增加，峰值法向应力的演化呈现出3 个阶段：第1 阶段，当法向刚度从0 增加到1 GPa/m时，峰值法向应力急剧增加；第2 阶段，当法向刚度从1 GPa/m 增加到2 GPa/m 时，峰值法向应力基本没有变化；第3 阶段，当法向刚度从2 GPa/m 增加到4 GPa/m时，法向刚度小幅度增加。同时起伏角从15°增加到45°时，对应的峰值法向应力增加值分别为0.01、0.18和0.41 MPa，呈现出逐渐增加的趋势。当起伏角为30°时，随着法向刚度的增加，峰值法向应力的演化呈现出2 个阶段：第1 阶段，当法向刚度从0 增加到1 GPa/m 时，峰值法向应力急剧增加；第2 阶段，随着法向刚度的增加，峰值法向应力几乎没有变化，这与图5(a)得到的结论一致。当起伏角为15°时，鉴于结构面上凸起体高度较小，对法向应力的敏感性较强，因此在图5 中对应的峰值剪切应力变化较大。

2.3 法向位移演化

不同起伏角结构面法向位移-剪切位移曲线，如图6 所示。

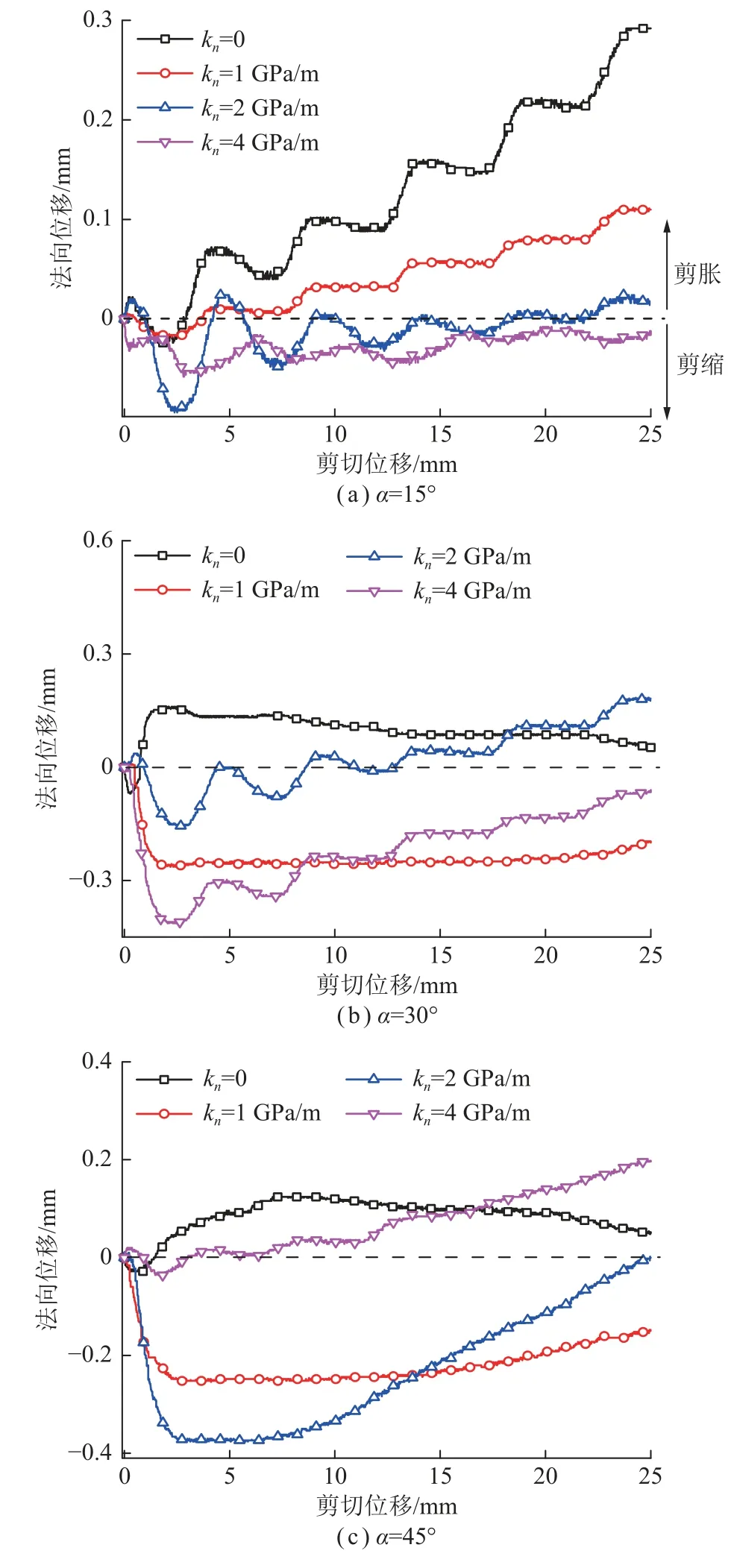
图6 法向位移-剪切位移曲线Fig.6 Normal displacement vs shear displacement curves

由图6 可以看出，法向位移和剪切应力的演化具有一一对应的关系。其中法向位移大于0 为剪胀，相反为剪缩。当起伏角为15°时，法向位移呈现出周期型震荡变化趋势，并且随着法向刚度的增加，结构面在剪切过程中剪胀量逐渐减小，呈现压缩趋势；当结构面起伏角为30°时，法向位移同样呈现出周期型震荡的变化趋势，在剪切结束时，法向位移基本上趋于稳定，几乎不发生变化；当结构面起伏角为45°时，法向位移不具有周期性，到剪切结束时，基本不发生变化。用峰值剪胀角演化来表征结构面在剪切过程中的法向位移变化，其计算方法为

式中，θmax为峰值剪胀角，( ° )；θ为剪胀角，( ° )。

不同起伏角结构面峰值剪胀角演化，如图7 所示。由图7 可知，随着法向刚度的增加，峰值剪胀角逐渐降低。当kn=4 GPa/m 时，3 种结构面起伏角的峰值剪胀角基本上相等，表明其对起伏角大小的依赖性较小。这是因为当剪切刚度较大，结构面发生全切齿破坏，在剪切过程中伴随着锯齿的完全剪断。随着起伏角的增加，结构面的峰值剪胀角逐渐增加，原因是：首先，由于结构面的起伏角不同，对应凸起体的高度不同；其次，由于起伏角不同，致使结构面在剪切过程中的破坏模式不同，使得峰值剪胀角的大小不同。

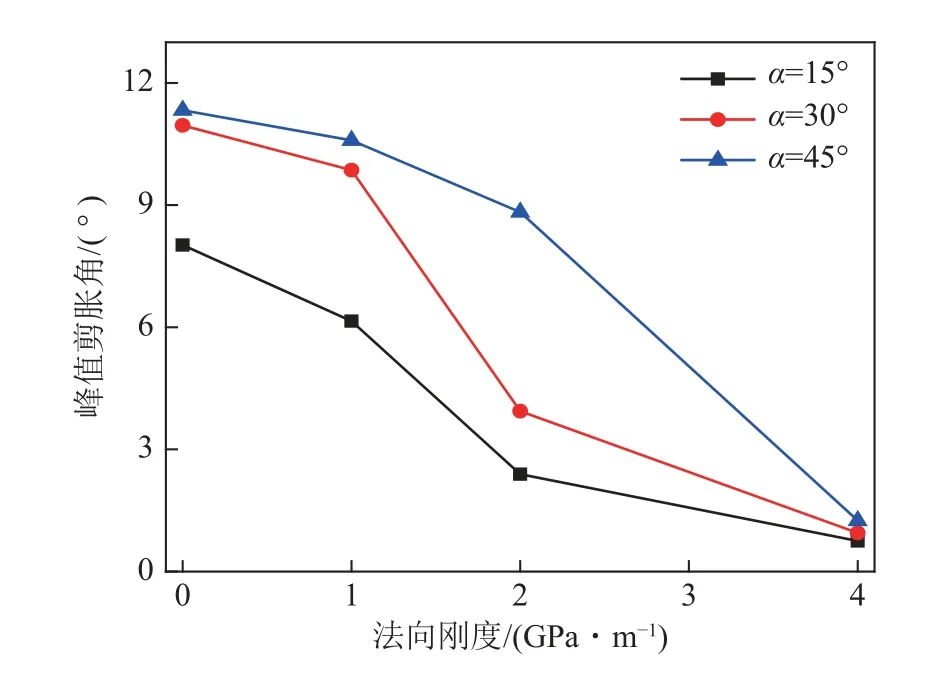
图7 峰值剪胀角演化Fig.7 Evolution of peak dilatancy angle

3 结构面破坏特征及形貌演化规律

通过以上分析得出，在不同起伏角和法向刚度条件下，结构面的剪切力学特性与破坏模式紧密相关。因此，分析不同条件下结构面的破坏模式显得至关重要。剪切前后结构面的三维形貌扫描，如图8 所示。由图可以看出，当结构面起伏角为15°时，由于结构面上凸起体高度较小，剪切过程中主要发生齿尖磨损破坏，具体表现为结构面上的部分凸起体有被磨损破坏的痕迹。随着法向刚度的增加，结构面的磨损程度逐渐增加。当起伏角为45°时，因为结构面上凸起体高度较大，发生爬坡破坏的可能性较低，所以一般表现为切齿破坏。当法向刚度较小时，因为凸起体之间的凹陷部分依然存在，所以结构面会发生齿尖剪断破坏，随着法向刚度的增加，结构面高度的最小值增加，也说明发生完全切齿破坏，并且由于法向应力的作用，使得剪断的凸起体被压碎并充填在结构面之间，使得结构面高度增加。当起伏角为30°，法向刚度从1 GPa/m 增加到2 GPa/m 时，结构面发生齿尖剪断破坏到部分凸起体被剪断破坏，之后随着法向刚度的增加，结构面上凸起体基本上全被剪断，并且没有发生较大的变化。通过结构面三维扫描，可以直观看出结构面的破坏方式，并且可以与剪切力学性质相对应。因为剪切后结构面发生破坏，所以对应剪切前后结构面的质量会发生变化。因此，可以用剪切前后结构面的质量变化来说明结构面的破坏，如图9所示。

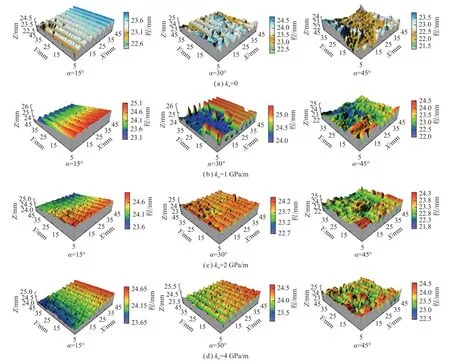
图8 结构面三维形貌扫描Fig.8 3D morphology scanning of structural plane

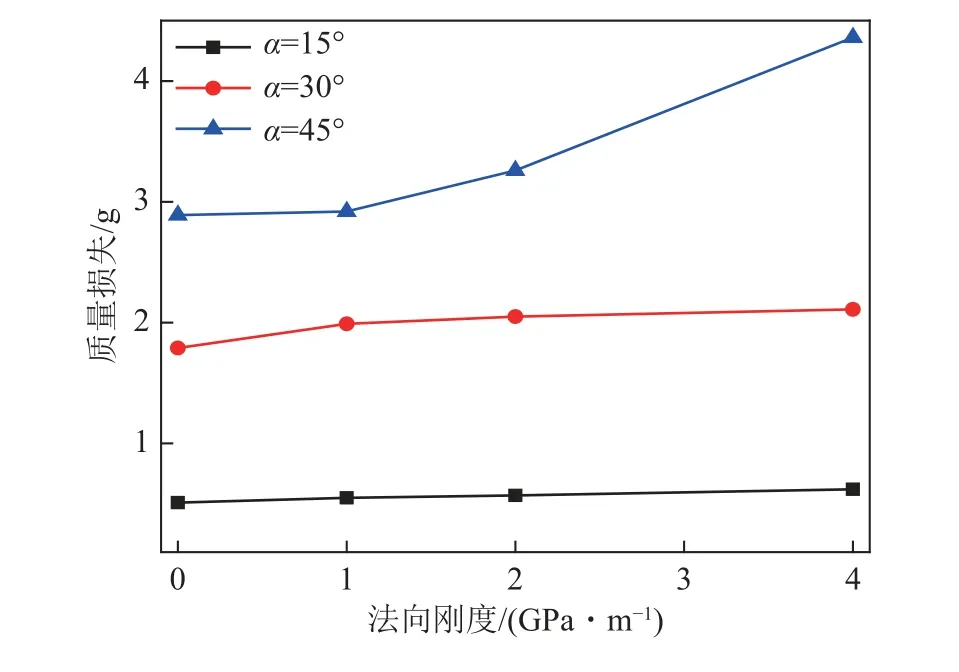
图9 结构面质量损失Fig.9 Mass loss of structural plane

由图9 可以看出，随着法向刚度和起伏角的增加，结构面的质量损失均逐渐增加，具体表现为：当起伏角为15°时，结构面的质量损失增加量较低。当法向刚度从0 增加到4 GPa/m 时，质量损失只增加了0.11 g，表明结构面破坏程度较低，因此只发生磨损破坏。当起伏角为45°，法向刚度从0 增加到4 GPa/m时，质量损失增加了1.47 g，变化量较大，因此发生切齿破坏，同时破坏并没有达到稳定。当起伏角为30°，法向刚度从0 增加到4 GPa/m 时，质量损失增加了0.47 g，介于2 个起伏角之间，其主要变化发生在法向刚度0～1 GPa/m，之后随着法向刚度的增加，质量损失不再发生变化，表明结构面的破坏已经达到稳定。综合以上分析看出结构面质量损失演化与峰值法向应力演化具有一一对应关系，因此可以用质量演化说明破坏模式。

通过分析剪切后结构面产生碎屑粒径的占比[35-37]，也可以得到结构面的破坏模式。试验后将取出的碎屑倒入到筛网中，筛网摆放位置从上到下分别为10 目(2 mm)、30 目(0.6 mm)和底盘，经过充分筛分后，将不同目数碎屑分别进行称重，可得到不同粒径碎屑的质量。将大于10 目(大于2 mm)、10～30目(0.6～2 mm)以及小于30 目(小于0.6 mm)碎屑粒径分别定义为第Ⅰ类、第Ⅱ类和第Ⅲ类碎屑。因为起伏角15°结构面产生的碎屑粒径都较小并且较为统一，对其进行筛分的意义不大，所以只针对起伏角45°结构面碎屑粒径质量分布进行分析，如图10 所示。由图10 可以看出，随着法向刚度的增加，第Ⅰ类碎屑的占比都是最低的，当法向刚度小于4 GPa/m 时，第Ⅲ类碎屑占比都达到50%以上；当法向刚度为4 GPa/m时，第Ⅱ类碎屑占比达到50%以上。随着法向刚度的增加，碎屑粒径占比的波动幅度不大，因此结构面发生的破坏模式较为统一，为切齿破坏。碎屑粒径占比具有波动的原因是：法向刚度与法向应力相对应，在剪切过程中产生的碎屑可能被压碎，因此造成了占比的轻微变化。

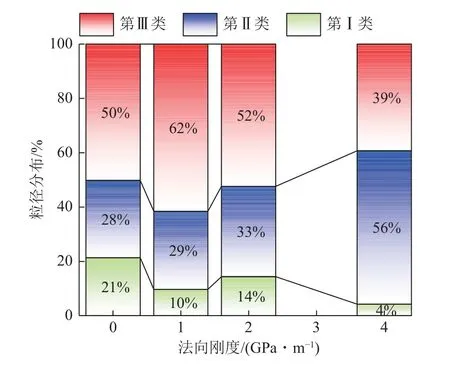
图10 碎屑粒径占比Fig.10 Percentage of clastic particle size

针对三维扫描得到结构面的空间点云数据，通过MATLB 编程计算，可以得到结构面的三维形貌参数。鉴于篇幅及形貌参数演化规律[38]，笔者主要分析的三维形貌参数如下：

(1) 平均高度z3：结构面上各点高度的平均值。

(2) 表面最大高差Sh：结构面最高点到最低点的垂直距离。

(3) 表面最大峰高Sp：结构面最高点到基准面的距离。

(4) 轮廓面积比SA：结构面的表面展开面积与垂直投影面积的比值，计算公式为

式中，St为表面展开面积；Sn为表面沿法向方向垂直投影到底面的面积。

(5) 体积V：结构面与底部平面所围成空间的体积。

(6) 表面积St：结构面的表面展开面积。

以起伏角15°为例，分析结构面三维形貌参数演化，如图11 所示，可以看出，随着法向刚度的增加，三维形貌参数都呈现出减速度降低的变化趋势。表明随着法向刚度的增加，结构面破坏程度增加，对应结构面磨损程度增加。根据式(1)、(2)可知，力学参数z3与结构面力学性质有较大的联系，因此现主要分析z3的变化趋势。可以看出当剪切刚度从0 增加到2 GPa/m 时，z3持续降低，当剪切刚度从2 增加到4 GPa/m 时，z3几乎没有发生变化，对应图5(a)和图5(c)，同样看出峰值剪切应力和峰值法向应力几乎没有变化。根据SA的定义，可以看出随着法向刚度的增加，结构面逐渐趋于平缓，对应结构面的破坏加剧。因此结构面的破坏与形貌参数演化具有一一对应关系。

图11 三维形貌参数演化Fig.11 Evolution of 3D morphology parameters

4 结构面动态破坏过程

通过结构面的空间点云数据，可以得到上下结构面各点在同一空间坐标系中的坐标。通过结构面点云数据和法向位移的变化，使用MATLAB 编程分别计算上下两结构面上每个标识点在不同剪切位移时的空间位置，进而可以分析结构面在剪切过程中的隙宽分布和演化规律。在结构面发生剪切错动时，上下结构面各点处的间距相应变化，且由于结构面的剪胀效应，裂隙间距也会受到一定影响。隙宽是指上下结构面间距随空间的分布情况，其在数值上等于上下结构面处各点i(x,y)的Z轴坐标之差，即

式中，Δi为点i(x,y)处的隙宽；ziu为上结构面在点i(x,y)处的高度；zid为下结构面在点i(x,y)处的高度。

当剪切位移un=0 mm 时，上下结构面的空间坐标点分别为iou(x,y,z)和iod(x,y,z)。对于剪切位移un=0 mm 时的隙宽分布情况，ziou和ziod就是ziu和zid，因此可以将ziou和ziod代入式(6)直接进行计算。对于剪切位移un≠0 mm 时的隙宽分布情况，其坐标沿剪切方向发生平移，因此需要通过坐标变换来计算任意剪切位移un时上下结构面的坐标。剪切位移为un时结构面上各点的隙宽可推导为

式中，ziou为初始状态时上结构面在点i处的高度；ziod为初始状态时下结构面在点i处的高度；z(i+u)ou为初始状态时上结构面在点(i+u)处的高度；δn为剪切位移为un时的法向位移。

结构面隙宽演化破坏判别机理，如图12 所示。当剪切位移为0 mm 时，如图12(a)所示，因为只有法向应力作用，所以结构面紧密闭合，对应隙宽较小且分布较为均匀。当剪切位移为2.5 mm 时，如图12(b)所示，结构面隙宽分布分为2 种情况：第1 种为上结构面齿底和下结构面齿尖接触，此时隙宽为两边高正中心处最低，并且由两边向中心逐渐减小。如果此时结构面发生破坏，则在中心处隙宽值会小幅度增加；第2 种为上结构面齿尖和下结构面齿底相对应，此时隙宽演化为两边低正中心处最高，并且由两边向中心逐渐增加。若发生切齿破坏，切断的凸起体充填在结构面之间，会使得齿底高度增加，则隙宽值有所降低。当剪切位移为5 mm 时，如图12(c)所示，上下结构面吻合，与剪切位移为0 mm 相比较，若此时结构面发生齿尖磨损或切齿破坏，在齿尖附近的隙宽值较大，且由两边向中心处逐渐增加；如果结构面没有发生较大程度的破坏，则结构面隙宽分布较为均匀。在此之后随着剪切位移的增加，结构面的隙宽演化分析与以上分析相同，因此可以通过结构面的隙宽演化与破坏模式相对应。

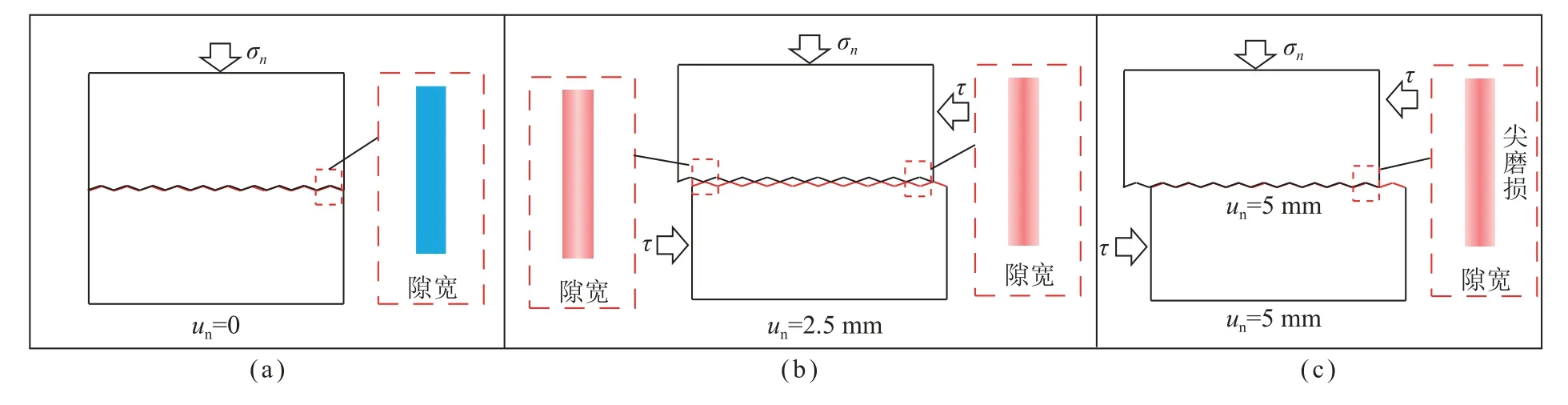
图12 结构面破坏判别机理Fig.12 Mechanism of structural plane failure discrimination

综上所述，假若在特定剪切位置处对应的结构面隙宽演化发生改变，则表明结构面发生了破坏，同时可根据隙宽分布情况判别结构面发生的破坏模式。

与图12 中的分析相对应，本文中结构面在X和Y正方向的采样范围均为5～45 mm，采样间隔均为0.125 mm。不同起伏角结构面在法向刚度4 GPa/m时的动态剪切破坏过程，如图13 所示。此处只对剪切位移un=0、2.5、5.0、7.5、10 mm 处进行分析。由图13 可以看出，当起伏角为15°时，结构面在剪切过程中，隙宽较大值出现在凸起体上，对应剪切位移不同，结构面的隙宽大小具有不均匀性，与图8 中结构面的破坏相对应。可以看出结构面的破坏是沿着剪切位移正方向由前向后进行传递的。在施加剪切位移时，前端的凸起体先承担剪切应力发生破坏，随着剪切位移的增加，结构面上的凸起体的破坏由前向后进行传递，但是大隙宽值和面积的占比不大，表明凸起体的磨损不大，这也是造成剪切应力具有周期性震荡演化的重要原因。

图13 结构面动态破坏过程Fig.13 Dynamic failure process of structural plane

当起伏角为45°时，可以看出随着剪切位移增加，隙宽较大值的位置几乎不变，表明当剪切位移为2.5 mm 时，结构面上的凸起体已经被完全剪断，破坏已经达到稳定，即隙宽较大区域在较小的剪切位移下已经达到稳定，不会随着剪切位移的增加有所改变，同样验证了结构面发生切齿破坏。

当结构面起伏角为30°时，可以看出结构面隙宽变化介于起伏角为15°～45°。当剪切位移从0 增加到5.0 mm 时，隙宽明显降低；对比剪切位移5.0 mm和10 mm 处的隙宽，两者并没有变化，说明结构面的破坏已经达到稳定；同时对比剪切位移2.5 mm 和7.5 mm 处结构面的隙宽可以再次得到相同的结论。表明在剪切位移为5.0 mm 之前，结构面上的凸起体已经被完全剪断，之后随着剪切位移的增加，结构面不会发生较大程度的破坏。通过以上对结构面隙宽演化规律分析得出的结论与其剪切力学性质完全呼应，从而验证了结构面的损伤演化特性。

5 结 论

(1)当起伏角为15°和30°时，曲线呈现周期性震荡衰减；起伏角为45°时，剪切应力在达到峰值后迅速降低，法向位移和剪切应力的演化具有一一对应关系。起伏角15°和45°结构面的峰值剪切应力呈现出线性增加的变化趋势；当起伏角为30°时，峰值剪切应力与法向刚度之间没有明显的线性关系，呈现出分段函数的特征。随着起伏角的增加，剪切刚度逐渐增加。随着法向刚度的增加，结构面峰值剪胀角逐渐降低，峰值法向应力呈现出两阶段的增加方式。

(2)当起伏角为15°时，结构面在剪切过程中主要发生磨损破坏。当起伏角为45°时，结构面表现为切齿破坏。当结构面起伏角为30°，法向刚度较低时，结构面发生磨损及切齿的复合破坏模式，之后随着法向刚度的增加，结构面发生切齿破坏。随着法向刚度的增加，质量损失逐渐增加，而三维形貌参数呈减速度降低，对应结构面的破坏程度逐渐增加。

(3)通过特定剪切位移处结构面的隙宽演化提出结构面的破坏判别机理，得出结构面的破坏是沿着剪切方向由前向后进行传递，前面的凸起体首先承受剪切应力发生破坏。随着剪切位移的增加，结构面上的凸起体的破坏同样由前向后进行传递，这也使得剪切应力演化具有周期性震荡衰减，从而验证了结构面的剪切损伤演化规律。