电磁场中螺旋线和旋轮线成因及特点的研究
马仕彪
(安徽省濉溪中学 安徽 淮北 235100)
带电粒子在电磁场中运动时,适当控制电磁场和粒子运动的方向,粒子的轨迹可以形成螺旋线和旋轮线,我们首先研究螺旋线[1].
1 螺旋线
1.1 等螺距螺旋线
如图1所示,一电荷量为+q、质量为m带电粒子(不计重力)静置于直角坐标系xOy坐标原点O处,整个空间处于竖直向下、磁感应强度大小为B的匀强磁场中.现给粒子一与x轴夹角为θ斜向下的初速度v0.
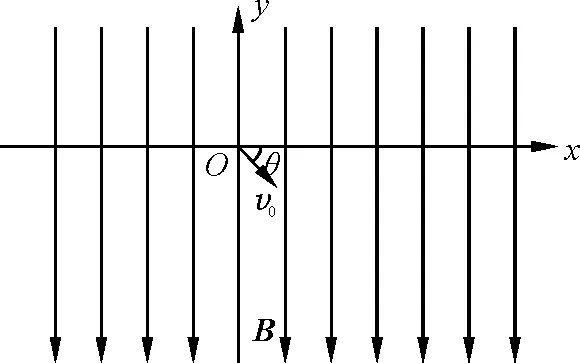
图1 粒子斜射入匀强磁场
因为粒子的速度与磁场方向不垂直,所以,将初速度v0分别沿水平和竖直方向进行分解.
带电粒子在水平方向上的分速度大小为
vx=v0cosθ
方向与磁场方向垂直,vx产生洛伦兹力的大小为
F洛=qvxB
该力提供粒子在水平方向上做匀速圆周运动的向心力,即
竖直方向上分速度大小为vy=v0sinθ,方向与磁场方向平行,因此vy不产生洛伦兹力,粒子在竖直方向上以速度vy=v0sinθ向下做匀速直线运动.
从合运动的角度看,粒子的合运动为等螺距的螺旋线运动,如图2所示,每两个相邻螺线之间距离即螺距.
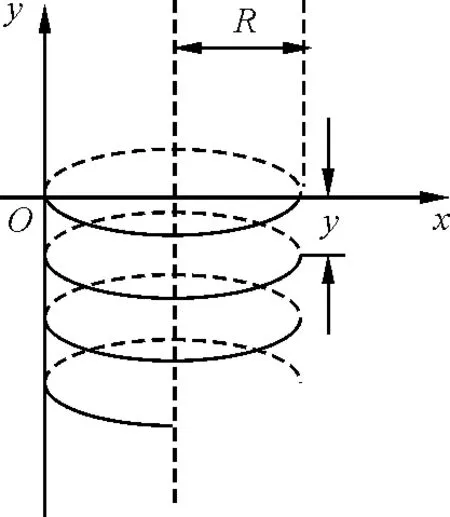
图2 等螺距螺旋线
1.2 螺距增加的螺旋线
在上述的情形下,若再加一个电场强度大小为E、方向竖直向下的匀强电场,其他条件不变,如图3所示.此时,带电粒子将同时受到水平方向的洛伦兹力和竖直向下的电场力作用.
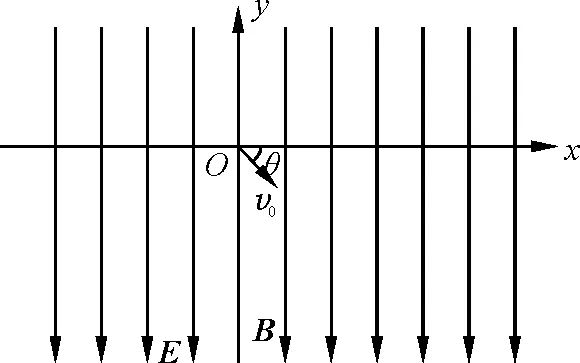
图3 粒子斜射入相互平行的电场和磁场
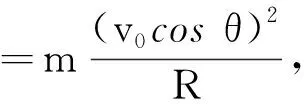
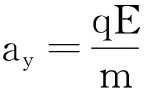
下落的高度
其轨迹形状如图4所示.
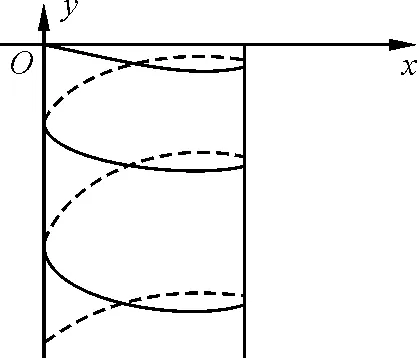
图4 螺距增加的螺旋线
通过以上分析可以看出,处理有关螺旋线问题时,可以采取运动的分解和合成的方法,这样就能化难为易.螺旋线的最大特征就是在时间和空间上具有一定的周期性,理解了周期性的来源和实质也就能解释和解决实际生活中的有关螺旋线的问题了,实现了理论和实践相结合的目的.
若继续改变电磁场的方向,使之两者方向互相垂直,带电粒子的轨迹将形成旋轮线.
2 旋轮线
2.1 粒子初速度为零的情况
如图5所示,空间存在相互垂直的匀强电场和匀强磁场,电场强度大小为E、方向沿y轴正方向,磁感应强度大小为B、方向沿z轴正方向.现有一质量为m、电荷量为+q的带电粒子(不计重力),从坐标原点O处由静止开始运动.

图5 粒子射入相互垂直的电磁场

(1)粒子运动的轨迹[2]
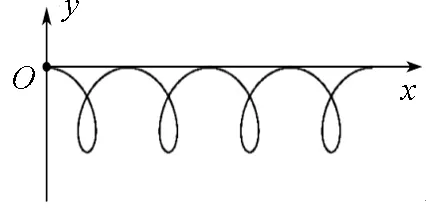
粒子的路径相当于动圆上的一个定点在做纯滚动运动时留下的轨迹,此轨迹线为周期性重复的旋轮线,如图6所示.
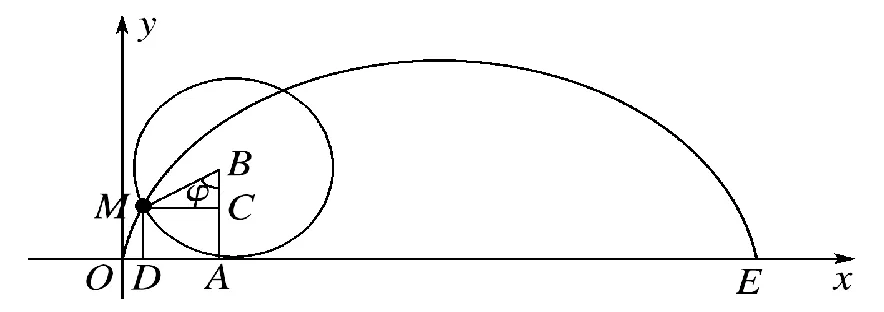
图6 旋轮线
(2)粒子的位移[3]
旋轮线的周期为粒子匀速圆周运动的周期,即
设粒子圆周运动在t时间内转过的角度为φ,由角速度定义式
粒子的半径
在x方向上的位移
(1)
在y方向上的位移
(2)
由以上计算结果并结合几何知识可以得到以下几个结论:
①旋轮线的高为圆周运动的直径
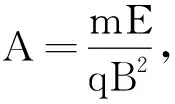
④ 由式(1)可知粒子在x方向上的运动为简谐运动和匀速直线运动的合成.
(3)粒子的速度
粒子在x方向上的速度
在y方向上的速度
合速度
(3)
现讨论粒子的最大速度vm.
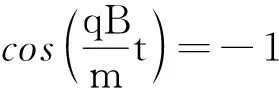
方法2:因为洛伦兹力永远不做功,只有电场力对粒子做功,在顶点处粒子沿电场力方向位移最大,所以粒子在旋轮线顶点时电场力做功最大,粒子的速度最大,由动能定理
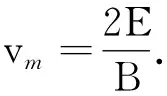
方法3:粒子在轨迹的最高点时,两个分速度同向,合速度最大,最大值为
2.2 粒子以初速度v沿x轴向右运动情况
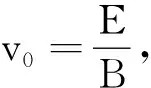
旋轮线的高为
每一拱旋轮线的宽度为
旋轮线与x轴交点为
现研究粒子以大小不同的初速度v向右运动的粒子轨迹情况.
(1)若速度Δv>0,则Δv方向向右,Δv产生的洛伦兹力使粒子在x轴下方以顺时针方向匀速圆周运动,下面分情况讨论.
①如果满足0<Δv=v0,粒子轨迹最低点的合速度为零,轨迹如图7所示.
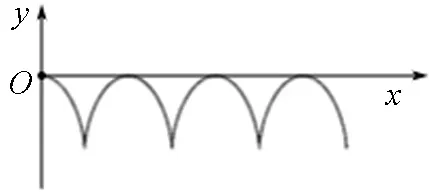
图7 Δv=v0时粒子轨迹
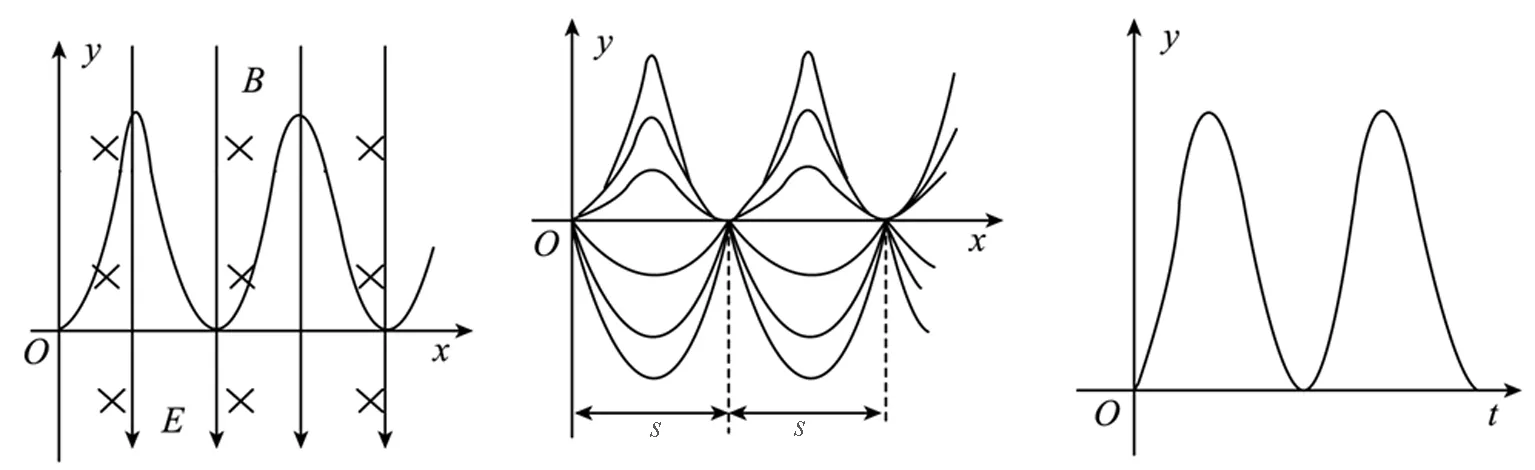
②如果满足0<Δv 图8 Δv ③如果满足Δv>v0,粒子轨迹最低点的合速度向左,轨迹如图9所示. 图9 Δv>v0时粒子轨迹 (2)若速度Δv<0,则Δv方向向左,Δv产生的洛伦兹力使粒子在x轴上方以速率Δv顺时针方向做匀速圆周运动,轨迹如图10所示. 图10 Δv<0时粒子轨迹 【例3】(2011年福建高考题改编)如图11(a)所示,在x>0的空间中存在沿y轴负方向的匀强电场和垂直于xOy平面向里的匀强磁场,电场强度大小为E,磁感应强度大小为B.一质量为m、电荷量为q(q>0)的粒子从坐标原点O处以初速度v0沿x轴正方向射入,粒子的运动轨迹如图11(a)所示,不计粒子的重力.现只改变入射粒子初速度的大小,发现初速度大小不同的粒子虽然运动轨迹不同,但具有相同的空间周期性,如图11(b)所示. (a) (b) (c)图11 初速度大小不同的粒子运动 (1)求粒子在一个周期T内沿x轴方向前进的距离S; (2)当入射粒子的初速度大小为v0时,其y-t图像如图11(c)所示,写出y-t的函数表达式. (2)在y方向上,由图11(c)可以看出旋轮线向上偏,说明Δv=v0-v1>0. y-t函数表达式为 其中 为y方向上的简谐运动的振幅. 凡事只要能从原理和本质出发,就能做到大道至简,对问题的认知不仅能知其然更能知其所以然.“螺旋线”和“旋轮线”规律性很强,向我们展现了曲线的美感,解决方法归根结底就是运动的合成与分解.抓住螺旋线和旋轮线这两根线,让它逐渐延伸,打通物理的任督二脉,我们会发现“物理真是迷人”.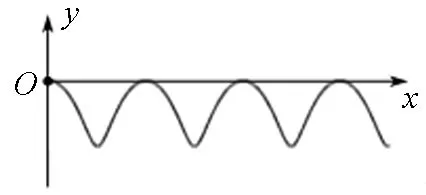

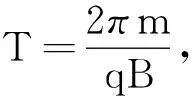
3 结束语

