混凝土搅拌车拌筒叶片螺旋线的设计研究

裴志军/PEI Zhi-jun

（1.华菱星马汽车（集团）股份有限公司，安徽 马鞍山 243061；2.合肥工业大学 机械与汽车工程学院，安徽 合肥 230002）

混凝土搅拌运输车核心部件是搅拌筒叶片，而决定叶片形状的螺旋线是决定混凝土搅拌、出料及其匀质性的关键因素。而螺旋线的数学模型以及参数是搅拌筒螺旋叶片的设计关键。文献1、2对螺旋线螺旋角的求取做了数学推导，但锥体部分螺旋角是变化的，利用求取螺旋线离散点处的螺旋角以及坐标，来拟合螺旋曲线，计算量大且螺旋线不光顺连续。

本文即针对文献1、2锥体变化螺旋角的螺旋线给出数学模型，并利用Pro/E软件的参数关系表达式，将该类变化螺旋角的螺旋线建立数模。

1 搅拌筒螺旋线分析

文献2将各区段螺旋线端点螺旋角做出列表。前锥段螺旋线小端处螺旋角βa为76.71°，大端处螺旋角βb为69.97°，可以看出螺旋角是变化的，且变化规律是由锥体小端至大端逐渐增大（图1）。尾锥部分，小端处螺旋线螺旋角βd为77°，大端处螺旋线螺旋角βc为71°，螺旋角的变化规律是由大逐渐变小。圆柱部分螺旋角为68.67°，为等螺旋角螺旋线（即阿基米德螺旋线）。锥体部分，通过取多个离散点计算，结果表明，a、b之间各点螺旋角值接近线性关系（图1、图2），文献2未能给出该螺旋线的数学模型。本文根据相关已知条件推导出该数学模型。

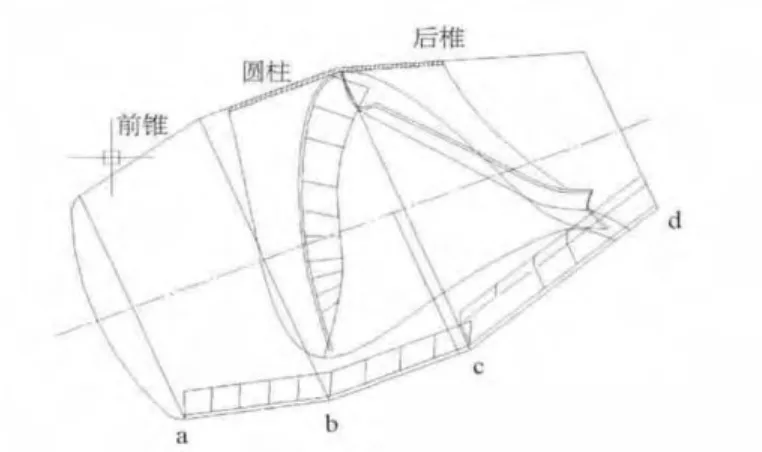
图1 筒体示意图

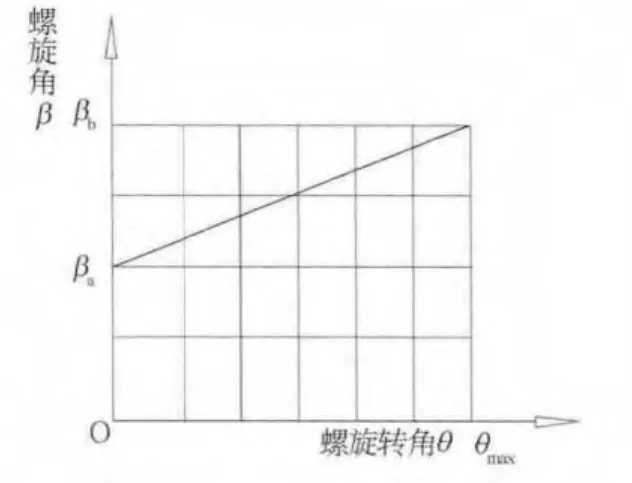
图2 线性变化螺旋角示意图

2 线性变化圆锥螺旋线推导

图3为搅拌车螺旋线示意图。

可将螺旋线上任一点的螺旋角表达为

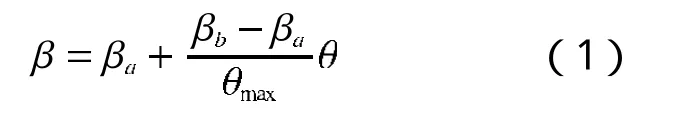
其中θmax为螺旋线在锥体上的最大转角，θ为螺旋线上任一点的转角值。

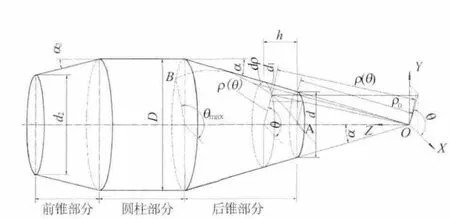
图3 圆锥螺旋线示意图

图3中的几何关系

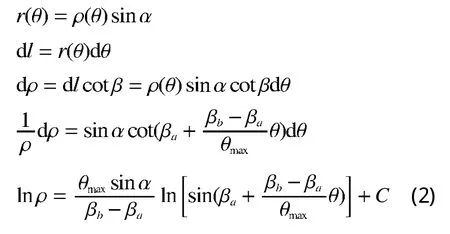
利用边界条件求常数C

当θ=0时代入上式可得

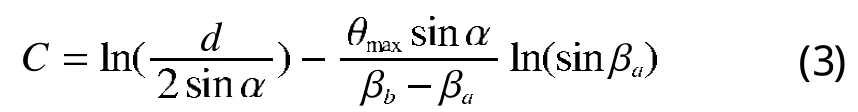
将式3代入式2，可得线性变化螺旋线方程

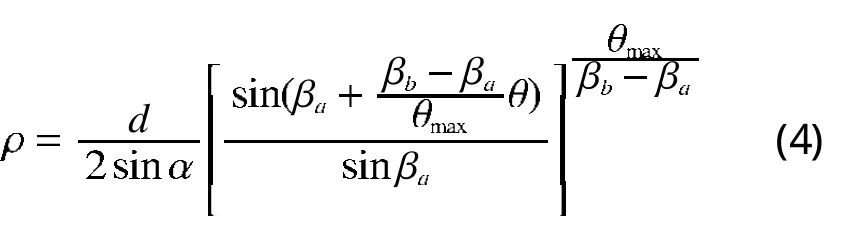
当θ=θmax时

将上式代入式4，可得

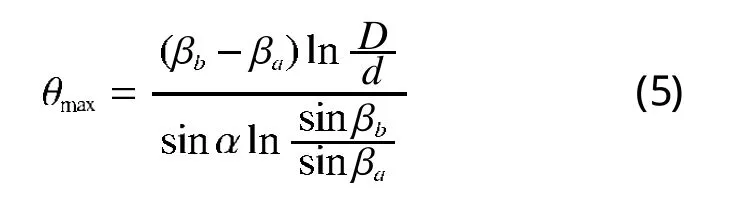
故，可将线性变化的圆锥螺旋线用参数方程表达如下

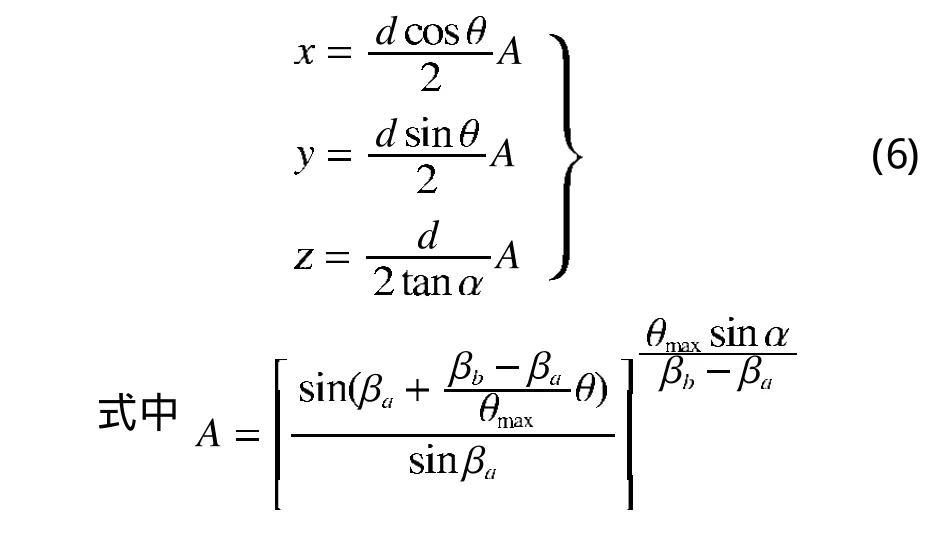
3 线性变化圆锥螺旋线在Pro/E中实现

以文献2中前锥线性关系螺旋角螺旋线参数为已知条件。用Pro/E中关系参数表达式建立数模如下

建立好坐标系，生成螺旋线数模，测量两个端点的螺旋角，符合文献2计算所得端点之螺旋角值。

4 结 语

本文根据文献2提出的圆锥螺旋角在圆锥大端和小端的值不同，建立了螺旋角线性变化的数学模型，并通过三维设计软件Pro/E的表达式程序，实现了线性变化螺旋角的建模，大大减少了设计计算工作量，并保证了筒体螺旋线的光顺性，为混凝土搅拌运输车螺旋叶片的设计提供了有益的设计参考。

[1]杨纪明.混凝土搅拌运输车搅拌筒螺旋叶片的设计（上）[J].建筑机械化，1984，(2)：8-15.

[2]杨纪明.混凝土搅拌运输车搅拌筒螺旋叶片的设计（下）[J].建筑机械化，1984，(3)：19-24.